合作引领是数学课堂教学有效性的体现

讷河市育才学校 代景美

合作引领是数学课堂教学有效性的体现

讷河市育才学校 代景美

一、教学目标：

1.知识目标：经历探索两个圆位置关系的过程；了解圆和圆之间的几种位置关系；了解两圆外切、内切与两圆圆心距d、半径R和r的数量关系的联系.

2.能力目标：培养学生的观察、想象、分析、动手操作、概括的能力和“类比、分类讨论”数学思想.

3.情感目标：体现数学学习的快乐，在快乐中体现知识源于实践，又运用于生活.同时培养学生运用类比的思想解决生活问题的能力.

二、教学重点、难点：

重点：识别圆和圆的位置关系及判定.

难点：圆心距与两圆半径之间的数量关系来判定两圆的位置关系.

三、教学方法：类比引领，合作探究.

四、教学手段：

课件、细铁丝制作的圆、硬纸片制作的圆、硬币两枚、圆规、直尺等.

五、教学过程实录：

（一）基础铺垫，设疑导入.

1.复习旧知：请说出点与点、点与线、点与圆、直线与圆的位置关系，并分别说出判定方法.

2.引入新课：（播放课件展示下列图形：奥运会五环旗、自行车、转轮.）

师：请观察自行车的前后车轮，他们是什么图形？反映了什么位置关系？

生：自行车的两个车轮是两圆，且没有交点.

师：奥运会五环旗上面有什么图形？他们反映了什么位置关系？

生：是圆的相交关系.

师：齿轮又有什么图形？（学生很容易看出他们的位置关系）

师：圆与圆有几种位置关系？如何来识别它们的位置关系？这就是我们今天要学习的主要内容：圆与圆的位置关系.（板书课题.）

（二）积极探究，获取新知.

【探究一】两圆的位置关系

问题1：圆和圆有哪些位置关系？（分组讨论.）

教师课前布置好：每人都在纸上画一个半径为2cm的圆，给每个人都发一个用细铁丝做好的圆圈当另一个圆，在纸上移动圆圈，让学生观察两圆的位置关系和公共点的个数.让学生自己画出可能出现的几种情况，并标清交点的个数.

（1）如果两个圆__公共点，那么就说这两个圆____，包括____和.

（2）如果两个圆__公共点，那么就说这两个圆___，包括____和____.其中___是____的一种特例.

（3）如果两个圆有___公共点，那么就说这两个.

问题2：试着描述两圆的各种位置关系.师生共同总结：外离、外切、相交、内切、内含.

师：我这里有两个大小不同的圆，请两位同学上来给大家演示一下两圆有几种位置关系？请大家认真观察两圆从远到近的运动，归纳他们的交点情况.

生：两圆外离，两圆没有交点.（演示.）

生：两圆外切，两圆只有一个交点.（演示.）

师：这个交点叫什么？

生：切点.

生：两圆相交，两圆有两个交点.（演示两圆相交）

生：两圆内切，两圆只有一个交点（两圆相内切教师指导.）

生：两圆内含，两圆没有交点（教师指导.）

师：请同学们观察总结，两圆有几种位置关系？生：5种.

师：直线与圆有几种位置关系？

生：3种：相离、相切和相交.

师：圆与圆是否还可以另外划分呢？（与直线和圆的位置关系相对应.）

生：圆与圆的位置关系也可以划分为3种：相离、相切和相交.

师：这是以什么划分的呢？

生：以两圆的交点个数来划分.

师：这里的相离和相切与前面学习的相离和相切相同吗？

生：不同，这里的相离包括两种：外离和内含，相切包括两种：外切和内切.

教师总结两圆5种分法和3种分法，给出结构图.

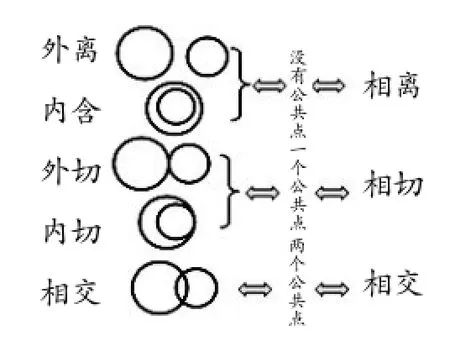
【探究二】探索d和r、R的数量关系.

如果两圆的半径分别是r1和r2（r1＜r2），圆心距（两圆的圆心距离）为d，当两圆外切时d与r1和r2有怎样的关系？反过来，d与r1和r2满足怎样的关系时，两圆一定外切？

进一步利用d与r1和r2之间的关系讨论两个圆的位置关系，并完成下表：

师：请同学们观察课件展示，归纳两圆的各种位置关系中，圆心距的变化与两圆半径之间的数量关系怎样？教师引领，全体学生共同回答：

（1）相外离时：d＞R+r；

（2）外切时：d=R+r；

（3）相交时：R-r＜d＜R+r；

（4）内切时：d=R-r；

（5）内含时：d＜R-r.

（教师用课件展示外离、外切、相交、内切和内含等五种位置关系，让学生总结两圆的半径、圆心距之间的关系，并将探索d和r、R的数量关系填入上表格中.）

（三）典型示范，强化训练.

1.例题解析

【例题】如图，⊙0的半径为5cm，点P是⊙0外一点，OP=8cm，求：（1）以P为圆心，作⊙P与⊙O外切，小圆P的半径是多少？（2）以P为圆心，作⊙P与⊙O内切，大圆P的半径是多少？

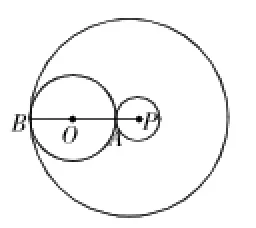
解：（1）设⊙O与⊙P外切于点A，则OP=OA+AP，AP=OP-OA，

∴PA=8-5=3cm.

（2）设⊙O与⊙P内切于点B，则OP=BP-OB，PB= OP+OB=8+5=13cm.

2.拓展训练题

（1）3个圆两两互相外切，它们的半径分别是1、2、3，则以3个圆心为顶点的三角形应是（）.

A.直角三角形B.锐角三角形

C.钝角三角形D.无法确定

（2）如图所示，两圆轮叠靠在墙边，已知两圆轮半径分别为4和1，则它们与墙的切点A，B间的距离为（）.

A.3B.8C.4D.5

（3）定圆O的半径是4cm，动圆P的半径是1cm.设⊙O和⊙P相外切，点P与点O的距离是多少？点P可以在什么样的线上移动？

（四）表格引领，课堂小结.

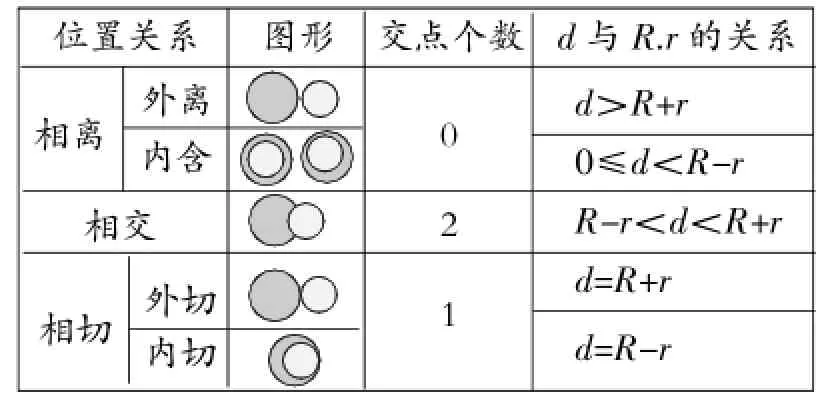
（五）重视基础，减负作业.

1.下列说法中，正确的是（）.

A.两个圆没有公共点时，叫做两个圆外离

B.两个圆有唯一公共点时，叫做两个圆外切

C.两圆有两个公共点时，叫做两圆相交

D.两圆内含就是两个圆是同心圆

2.⊙A、⊙B、⊙C两两外切，且半径分别为2cm、3cm、10cm，则△ABC的形状是（）.

A.锐角三角形B.直角三角形

C.钝角三角形D.等腰三角形

3.总结两圆位置关系的判定方法.要求作图说明.

两位教师来自不同学校，对本节课的认识都能以课程标准为依据，整合教材，结合本地实际将各自的教学风格，通过纪实、反思等手段实事求是地反应出来，对全省初中数学教学起到参考作用.教师们的课堂纪实细节处理得妙、教学反思说得真.