探究
——发现在解决教学重点、难点中的应用——以“平方差公式”课堂教学实录(二)为例
2014-02-17讷河市讷南镇中心学校
讷河市讷南镇中心学校
探究
——发现在解决教学重点、难点中的应用——以“平方差公式”课堂教学实录(二)为例
讷河市讷南镇中心学校杨东兴
(选自人教版义务教育课程标准实验教科书《数学》八年级上14.2.1平方差公式)本课采用“自主、合作与交流”课堂教学模式.
教学目标:
1.经历探索平方差公式的过程.
2.会推导平方差公式,运用公式进行简单的计算.
3.在计算中发现规律,并用符号表示,体会数学的简洁美.
教学重点:平方差公式的推导和应用.
教学难点:理解平方差公式并灵活运用平方差公式进行简单的计算,并能判断在何种情况下可以利用公式.
教学过程:
一、教师引领自主探究
问题1:(算一算)
师:我们学习过了整式的乘法,知道了两个多项式相乘的法则.今天我们要继续学习某些特殊情形下的多项式相乘.请大家应用所学的知识,自己来完成下面的问题:
(1)(x+1)(x-1)=
(2)(m+2)(m-2)=
(3)(2x+1)(2x-1)=
师:谁说说各题的结果?
生1:(x+1)(x-1)=x2-1
(m+2)(m-2)=m2-4
(2x+1)(2x-1)=4x2-1
师:在(m+2)(m-2)=m2-4等式中,4可以写成几平方?
生:2的平方.
师:也就是说(m+2)(m-2)=m2-22
(2x+1)(2x-1)=(2x)2-12
问题2:(猜一猜)
师:大家结合上面的计算结果,不计算,通过观察、比较,你来猜一下下面式子的结果.
(1)(x+6)(x-6)=
(2)(a+2)(a-2)=
(3)(x+y)(x-y)=
师:谁大胆猜猜各题的结果?说出你猜想的依据.
生:根据(m+2)(m+2)=m2-22这个式子的特点,我的猜想结果是这样的:
(1)(x+6)(x-6)=x2-62=x2-36
(2)(a+2)(a-2)=a2-22=a2-4
(3)(x+y)(x-y)=x2-y2
师:大家说他回答得好吗?
生:很好.
师:生3同学善于观察、善于思考、善于发现,回答得很精彩.大家要向他学习.
问题3:(说一说)
师:从上面的运算中大家发现了什么规律?
生:(a+b)(a-b)=a2-b2.
师:请王小明同学用自己的语言叙述所发现的规律.生:两个数的和乘以两个数的差,等于两个数的平方差.师:方才王小明同学表述得很流利.大家仔细分析一下,他表述的符合这个等式的含义吗?如不符合,应该怎样说?
生:不对呀,应该表述成:两个数的和乘以这两个数的差,等于这两个数的平方差,就差一个字.
师:你说得真有道理,你表述得也太科学了.一字之差,有时就会导致错误.可见科学来不得半点差错,一定认真思考、斟酌.
师:大家看一下这个等式结构特征.等式左边意思是?
生:两个数的和乘以这两个数的差.
师:等式右边的意思是?
生:这两个数的平方差.
师:大家说得都对.这个等式就叫平方差公式.是本节课学习的重点.大家一定要理解记忆.
问题4:(数形结合,推理论证)
师:你能用下面的几何图形来解释平方差公式吗?
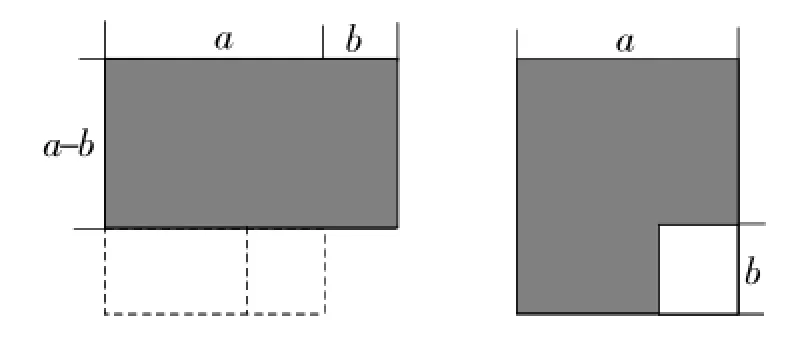
生:左边阴影部分面积等于右边阴影部分图形的面积.即(a+b)(a-b)=a2-b2.
师:很好,根据几何图形面积相等也论证了(a+b)(ab)=a2-b2这个规律是正确的.
师:这个内容就是我们今天要研究的内容.(板书课题:平方差公式.)
请学生快速记住公式,以便遇到类似形式的多项式相乘时就可以直接运用公式进行计算.在此基础上,让学生用自己语言叙述公式.师生共同得出相同项的平方减去不同项绝对值的平方.
二、师生互动,应用提升
师:现在我来解决一下课前的简算问题,你们现在知道该如何简算了吧,15秒内抢答.
生:(快速进行计算,并得出结果.)
第一小组:3999999.
第三小组:999996.
下面请同学们一起练习几道题,看你们是否能很快地做出来呢?
例1:运用平方差公式计算:
(1)(5x+7)(5x-7)
(2)(x+5y)(x-5y)
师:这两个题目是否符合平方差公式特征?(学生回答后,教师板书解题过程.)
师:下面我们再巩固一下,请大家试一试,口算:练一练:(1)(x+y)(x-y)
(2)(x+2)(x-2)
(3)(ab+c)(ab-c)
(4)(m+3n)(m-3n)
生:各小组抢答(准确率很高).
例2:计算(1)(5m+2y)(5m-2y)
(2)(3y-2)(2-3y)
(3)(-3+x)(-3-x)
教师引导学生分析题目条件是否符合平方差公式特征,并让学生说出本题中a,b分别表示什么.(巡视学生解题情况.)
师:哪组同学愿意把你的计算结果展示给大家?
生:(1)题能运用平方差公式,5m相当于a,2y相当于b.
师:大家判断得很准确,第(2)题呢?
生:不可以运用平方差进行计算,3y与-3y是互为相反数,2与-2也是互为相反数,所以,不能用平方差公式进行计算,运用多项式乘法计算.
师:这道题只能运用多项式乘法来进行计算了.同学们考虑一下(3)题呢?
生:能运用平方差公式计算,-3相当于a,x相当于b.
师:很好!大家掌握得非常扎实.
三、展示交流,突破难点(大屏幕打出)
1.判断下列多项式的乘法是否能用平方差公式计算.若能,请计算出结果;若不能,请说明理由.
(1)(a+5)(a-5)(2)(2a+3b)(3a-2b)
(3)[1+(x+y)][1-(x+y)](4)(a-x)(-a-x)
2.用平方差公式计算:
(1)(a+3)(a-3)(2)(2a+3b)(2a-3b)
(3)(a+5b)(a-5b)(4)(-5y-4x)(4x-5y)
让学生在练习本上计算,教师巡视各小组解题情况,每题让不同小组学生进行板演.
3.用简便方法计算:
(1)102×98(2)201×199
4.街心花园有一块边长为a米的正方形草坪,经统一规划后,东西要加长两米,而南北要缩短两米,问改造后的面积是多少?(教师巡视学生练习情况,请各小组不同解法的学生,或发生错误的学生板演,教师和学生一起分析解法.)
四、反思总结,质疑求学
师:我们能不能总结一下利用平方差公式计算应注意什么?学生发言后,小结:
(1)公式中的字母a、b可以表示数,也可以表示数的单项式,多项式即整式.
(2)要符合公式的结构特征才能运用平方差公式.
(3)有些多项式与多项式的乘法表面上不能应用公式,但通过加法或乘法的交换律、结合律适当变形就能应用公式.
师:这节课你有什么收获和体会?(学生以小组为单位,谈一谈通过本节课的学习你有哪些收获?)
生:(谈收获和体会.)
师:1.什么是平方差公式?
2.运用公式要注意什么?
五、布置作业,拓展新知
1.运用平方差公式计算:
(1)(2a-3b)(3b+2a)(2)(-1+3x)(-1-3x)
2.计算:
(1)(x+y)(x-y)+(2x+y)(2x+y)
(2)(2a-b)(2a+b)-(2b-3a)(3a+2b)
