流动阶段页岩油气典型曲线分段预测方法

白玉湖，王小林，陈桂华，徐兵祥，冯汝勇

(1.中海油研究总院，北京 100027;2.中海油国际有限公司，北京 100010)

引 言

页岩储层致密，水平井多级压裂是导致页岩油气产量递减预测区别于常规气藏的重要原因之一。确定页岩油气产量递减的方法主要包括解析方法、数值模拟方法[1-2]及典型曲线方法[3]。3种方法各有特点且适合于不同的开发阶段。目前工业界中应用最为广泛的是典型曲线方法。双曲递减是最常用的方法，但可能导致过高的后期产量预测。Ilk等提出幂律指数递减，但部分参数物理意义不够明确，拟合存在一定难度[4]。Seshadri等比较了修改的双曲递减方法和幂律指数方法，并指出了2种方法的优缺点[5]。Bello等提出了混合典型曲线的预测方法，但无法确定无限流动作用阶段结束的时间[6]。

综上所述，页岩油气典型曲线多种多样，且应用比较广泛，但由于页岩油气在经过复杂改造后，储层中的流动机理复杂，典型曲线方法尚需进一步完善。在分析页岩油气在储层中流动阶段基础上，针对不同流动阶段，提出了一种页岩油气典型曲线分段预测方法。

1 页岩油气在储层中的流动阶段划分

目前页岩油气的商业开发都是基于长水平井多级压裂技术，美国页岩油气田压裂级数常常在20～30级，甚至更长。如此大规模地压裂使得页岩油气在储层中流动复杂，并呈现不同的流动阶段，按时间先后顺序依次为双线性流、线性流、拟稳态流、后期边界线性流动[7]。其中双线性流阶段时间较短，为几个到几十个小时。线性流动阶段和拟稳态流动阶段持续时间长，是页岩油气生产过程中最主要的流动阶段。对于单井而言，上述的流动状态不一定完全存在，这依赖于系统性质，如裂缝长度、裂缝间距、基质渗透率以及SRV改造后的渗透率，一些流动阶段可能是缺失的。

2 页岩油气典型曲线分段预测方法

对于一般的页岩油气井而言，线性流动和拟稳态流动阶段是2个最主要的流动阶段，因此，可以采用分段典型曲线来预测油气产量，在线性流动阶段采用归整化压力和时间平方根的线性函数来预测递减规律，对于拟稳态流动阶段采用Arps递减，且拟稳态流动阶段也符合Arps递减要求的条件。分段预测典型曲线示意图如图1所示，在拟稳态流动阶段，乐观的递减为调和递减，保守的递减为指数递减。

图1 分段典型曲线示意图

在线性流动阶段，产量q和生产时间t满足如下关系式[8]:

其中

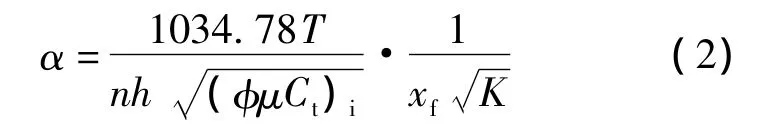
式中:m(pi)和m(pwf)分别为油气藏初始压力和井底流压下对应的拟压力，Pa2/Pa·s，对于页岩油而言，则直接以压力表示即可;q为产量，m3/d;t为生产时间，d;b为常数;α为斜率;n为压裂裂缝条数;h为储层厚度，m;xf为裂缝半长，m;K为基质渗透率，10-3μm2;φ为基质孔隙度;μ为流体黏度，mPa·s;Ct为储层综合压缩系数，Pa-1;T为温度，K;下标i表示原始油藏条件下。

将式(2)带入式(1)得:

在拟稳态流动阶段，可以采用Arps递减来描述。根据递减指数n的取值不同，Arps产量递减曲线可以分为指数递减、双曲递减和调和递减3种形式，具体如下:

双曲递减曲线为:

式中:D为递减率;n为递减指数;qi为初始产量，即为线性流动结束时的产量，m3/d。

指数递减曲线为:

调和递减曲线为:

从线性流转变为拟稳态流动的时间可以采用如下公式进行计算:

式中:tendl为线性流转变为拟稳态流动的时间，d;x为裂缝间距，m。

3 应用分析

3.1 无生产数据的新区典型曲线预测

有时需要对页岩油气新区块的产量进行预测，此时没有生产井和生产动态数据。根据对页岩油气井的初步设计以及对储层参数的认识，可以确定一些参数，比如储层基质渗透率、孔隙度、压缩系数、储层厚度、压裂级数、设计的裂缝半长等，根据这些参数可以粗略估算线性流动阶段的产量、从线性流到拟稳态流的时间。对于拟稳态流动的阶段Arps递减而言，难以确定其递减类型，但可以给出其递减函数范围，即最保守估计为指数递减，最乐观估计为调和递减。运用典型曲线分段预测方法可以得到如下的典型曲线:

当t＜tendl时

当t≥tendl时，保守估计的典型曲线为:q=qie-Dt，乐观估计典型曲线为:q=qi(1+Dt)-1。由此，可以确定新区典型曲线变化范围。

3.2 有生产数据的典型曲线预测

已有生产数据的页岩油气井分段典型曲线预测基本思路如下:根据生产数据作出[m(pi)-m(pwf)]/q和的关系图，并对数据点进行直线分析，如果能明显看出数据点偏离直线段，则可确定tendl，对于生产时间大于 tendl之后的数据点，采用Arps递减进行拟合，确定拟稳态阶段的典型曲线。如果直线未出现拐点，即还无法判断拟稳态流动阶段开始的时间，则采用式(7)预测tendl，对于tendl之后的阶段，由于没有实际数据点，则采用区间估计，即给出最保守的典型曲线和最乐观的典型曲线。

4 实例验证

选取一口美国页岩油气田页岩气井为例，分析该方法的可靠性，其产气生产动态如图2所示。

图2 Ealge Ford某页岩气井生产动态数据

该井主要参数如下:孔隙度为0.05，流体黏度为0.2 mPa·s，综合压缩系数为5.33×10-10Pa-1，渗透率为10-7μm2，裂缝间距为100 m，裂缝级数为18级，气藏温度为387 K，储层厚度为125 m，有效裂缝半长为43 m。把上述参数代入式 (3)，并对实际生产数据进行处理，结果如图3所示。由图3可知，理论预测呈直线，实际数据也呈很好的线性分布，说明该井处于线性流动阶段;理论预测和实际数据吻合度很好，这充分说明采用线性流动理论进行分析是可行的。根据该井的流体及分析资料，根据式 (7)，得到tendl=1 542 d，即当生产时间大于1 542 d时，递减规律转为Arps递减。

图3 某页岩气井归整化压力和生产时间平方根关系

5 结论

(1)根据页岩油气井长水平井多级压裂流动阶段特征，提出了一种页岩油气典型曲线的分段预测方法，即在线性流动阶段采用归整化压力和时间平方根的线性函数来预测递减规律，在拟稳态流动阶段采用Arps递减曲线进行预测，其中乐观的递减为调和递减，保守的递减为指数递减。

(2)针对所提出的典型曲线分段预测方法，给出了长水平井多级压裂从线性流动阶段转换为拟稳态流动阶段的理论时间估算方法。

(3)针对无生产数据的新区和有生产数据的页岩油气区，分别给出了分段典型曲线预测思路和方法。

(4)对实际页岩气井进行分析，理论预测的线性流动阶段和实际数据吻合，说明了该方法的适用性。

[1]Moghadam S，Mattar L，Pooladi-Darvish.Dual porosity typecurves for shale reservoir[C].CSUG/SPE137535，2010:1-12.

[2]Seshadri J，Mattar L.Comparison of Power law and modified hyperbolic decline methods[C].CSUG/SPE137320，2010:1-17.

[3]孙海，姚军，孙致学，等.页岩气数值模拟技术进展及展望[J]. 油气地质与采收率，2012，19(1):46-49.

[4]Ilk D，Rushing G A，Perego A D，et al.Exponential vs hyperbolic decline in tight gas sands-understanding the origin and implication for reserve estimates using arps decline curves[C].SPE116731，2008:1-22.

[5]Seshadri J，Mattar L.Comparison of power law and modified hyperbolic decline methods[C].CSUG/SPE137320，2010:1-15.

[6]Bello R O，Wattenbarger R A.Multi-stage hydraulically fractured shale gas rate transientanalysis[C].SPE126754，2010:1-17.

[7]Luo S Q，Neal L，Arulampalam P，et al.Flow region analysis of multi-stage hydraulically-fractured horizontal wells with reciprocal rate derivative function:Bakken case study[C].CSUG/SPE137514，2010:1-13.

[8]Nobakht M，Clarkson C R.A new analytical method for analyzing production data from shale gas reservoirs exhibiting linear flow:constant pressure production[C].SPE143989，2011:1-15.