重覆冰区线路不均匀脱冰的不平衡张力计算
2014-02-14郎需军杨茂亭李陶波
杨 博,郎需军,杨茂亭,陈 鹏,李陶波
(1.山东电力工程咨询院有限公司,济南市250013;2.山东理工大学,山东省淄博市255049)
0 引 言
我国是输电线路覆冰较为严重的国家之一,由于微气候特征多样,冬季的冻雨、冻雾天气频繁且极易形成混合淞覆冰,引起覆冰跳闸和倒塔事故[1-3],从而严重威胁输电线路安全运行。导线脱冰会引起导线跳跃上下摆动,导致导线档中空气间隙的减小,以致相间闪络;另一方面还会对铁塔产生较大的不平衡张力,在覆冰较厚、档距较大的情况下这种作用更为明显,容易对铁塔造成破坏。因此合理确定杆塔荷载,增强线路抗冰能力,准确计算不均匀脱冰产生的不平衡张力具有重要意义。
通常研究导线不均匀脱冰,国内外学者多借助有限元模型,并采用ANSYS 等软件进行数值仿真计算[4-7];此方法虽然考虑到影响不均匀脱冰的诸多因素,但不能形成简便实用的计算软件,不适用于实际工程设计工作所需的逐塔批量计算。传统等线长法可实现不均匀脱冰的不平衡张力计算[3]:一个耐张段架线完成后,总导线长度不变,由假设第1 档初始应力,一步步求得每一档应力,并同初始线长比较,根据比较结果反过来调整第1 档导线初始应力,不断循环逼近,逐步扫描试凑来求解各档应力。扫描试凑算法精度虽可靠,但每计算一点不平衡张力需上万或十几万次迭代,效率太低。
本文以浙北—福州1 000 kV 交流线路工程为算例,分析特高压线路覆冰不均匀脱落过程,仍采用“等线长法”计算模型,引入“扫描二分法”改进迭代算法,开发设计软件以实现对不均匀脱冰产生不平衡张力的高效精确计算,每计算一点不平衡张力只需几十次迭代。通过计算,对影响不平衡张力的绝缘子串长、导线型式、档距配置、高差、脱冰率等因素进行敏感性分析,验证计算结果并发现抑制重覆冰区不均匀脱冰的方法,进而减小不平衡张力。本文还对具有特殊性的孤立档进行计算和分析,考虑到耐张塔作为耐张段承力塔的重要性,建议耐张塔设计考虑非均匀脱冰模式下的不平衡张力[4]。
1 计算原理及模型
1.1 等线长法求解不平衡张力
导线架设时要保持连续档内各档应力相同,导线覆冰脱落时,不均匀外荷载将引起各档应力不同,使直线塔上出现不平衡张力;该不平衡张力使悬垂绝缘子串偏移后,虽可大为减小,但铁塔必需能够承受一定程度的纵向不平衡张力。不平衡张力需先求解连续档内非脱冰档和脱冰档的应力,单相导线不平衡张力ΔF=(非脱冰档应力σ-脱冰档应力σ)×导线截面积A×分裂根数N。
(1)档距变化与应力间的关系。假定连续档各直线塔上悬垂绝缘子串均处于中垂位置,各档导线应力均为σm。脱冰后各档应力不一致,导线悬挂点发生偏移,档距发生变化。可列出第i 档档距增量Δli与档内应力σi间的关系式[8-9]:
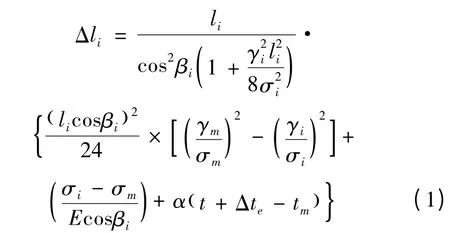
式中:li、βi分别为第i 档档距、高差角;γm、γi分别为脱冰前后的垂直比载;σm、σi分别为脱冰前后的应力;E为弹性系数;t 为计算不平衡张力时的气温;tm为导线架线时的气温;Δte为架线时考虑初伸长降低的等效温度。
(2)悬垂绝缘子串偏移与两侧导线应力间的关系。假定悬垂串为均布荷载的刚性直棒,如图1 所示,第i 基直线塔上悬垂串末端导线悬挂点的顺线路水平偏移δi与两侧导线应力差的关系[8-9]为
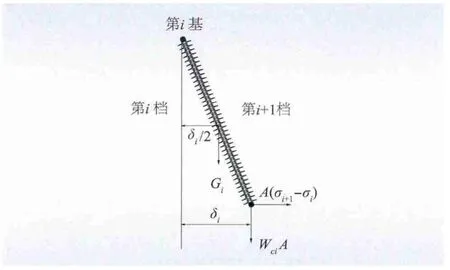
图1 悬垂绝缘子串受力偏移图Fig.1 Stress deviation of insulator string
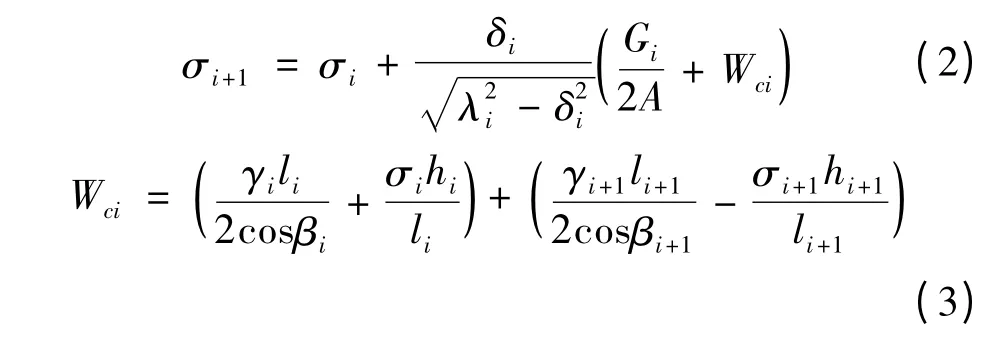
式中:σi、σi+1,li、li+1,hi、hi+1,βi、βi+1分别为第i档和第i+1 档内导线应力、档距、高差和高差角;λi、Gi分别为悬垂串串长及荷载。
(3)等线长法求各档导线应力。对于整个耐张段内,各档档距增量之和应为0,即第n 基杆塔(耐张塔)上导线悬挂点的偏距应为0。
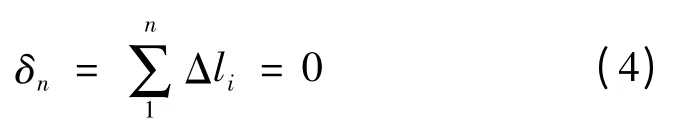
(4)各档档距增量间的关系。耐张段内有n 档,则有n-1 基直线塔。利用式(1)可列出n个方程,式(3)代入式(2)解出σi+1的显函数式则可列出n -1个方程,加上式(4),共计2n个方程。因此,Δl、σ共2n个未知数,是可以求解的。通常采用扫描试凑法求解,即自编号第1 档开始按如下顺序运算:σ1→式(1)→Δl1=δ1;δ1、σ1→式(2)→σ2;σ2→式(1)→Δl2;δ1+Δl2=δ2;δ2、σ2→式(2)→σ3;…;δn-1、σn-1→式(2)→σn;σn→式(1)→Δln;直至式(4)δn=δn-1+Δln=Δl1+Δl2+Δl3+…+Δln=0 即为最终解。当各档的Δl、σ 解出后,可求出相邻档间的不平衡张力差及各档的弧垂。
1.2 改进迭代算法
对于上述迭代法求解,如果步长选得过大,就有可能扫描不到实根或者在一个小区间内根不唯一,但如果步长选得过小,需要扫描的步数就会增多,从而使计算工作量过大。因此可采用“扫描二分法”[10-12]进行求解,其效率高、误差小;求解不平衡张力的算法如图2 所示,二分法迭代计算过程的曲线如图3所示。
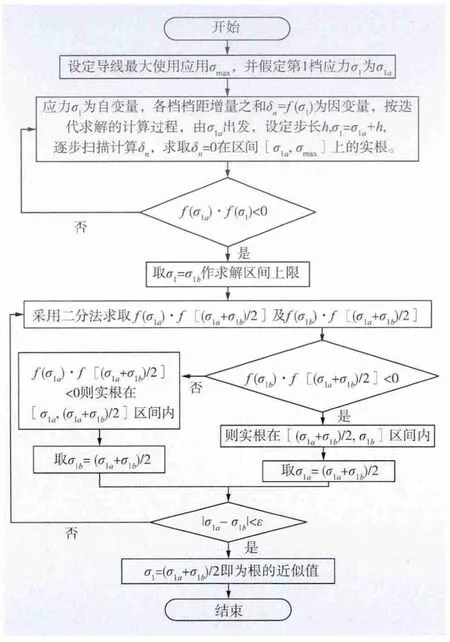
图2 算法流程Fig.2 Algorithm flow
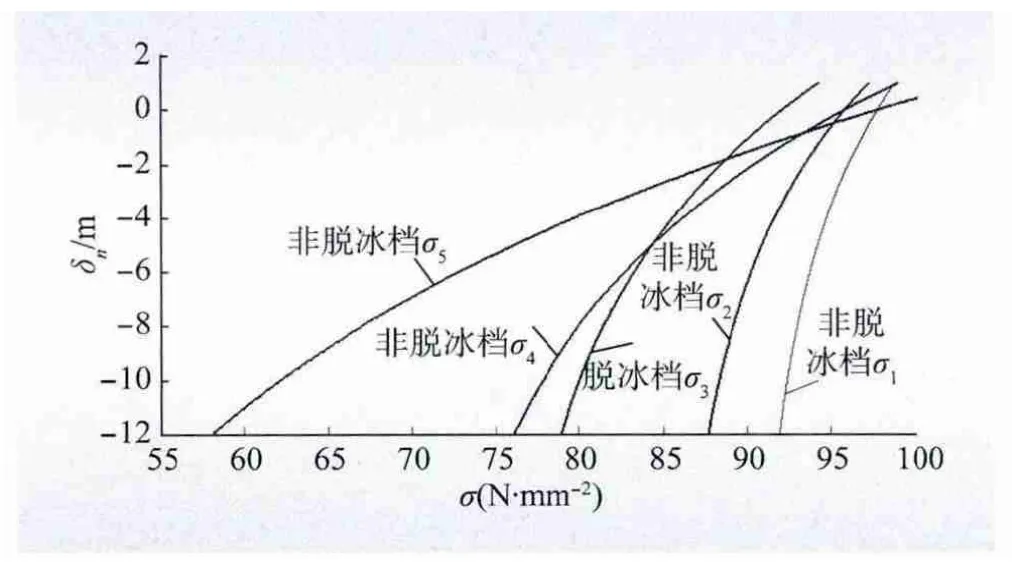
图3 迭代计算曲线Fig.3 Iterative calculation curves
图3迭代计算过程描述如下:若连续5 档,中间第3 档脱冰,导线最大使用应力σmax=103.44 N/mm2,假定脱冰后第1 档应力初值σ1=σ1a=92.0 N/mm2,求解各档档距之和δn=0 在区间(92.0,103.44)内的实根,采用迭代法,可得δn=f(92.0)= -12.0 <0,接着选取合适步长值并进行一次逐步扫描计算,求得σ1=98.82 N/mm2时,δn= f(98.82)= 1.02 >0;由 于f(92.0)·f(98.82)<0,故取σ1b=98.82 为上限,取(σ1a+σ1b)/2=(92.0 +98.82)/2 =95.41 为下限,又δn=f(95.41)= -2.91 <0,f(95.41)·f(98.82)<0,因此实根在区间(95.41,98.82)内;继续采用二分法取(σ1a+σ1b)/2=(95.41+98.82)/2=97.12 为下限,得δn=f(97.12)= -0.7 <0,重复二分法,实根区间逐渐减小,直至求得满足误差要求的近似真值。图3 中随着第1 档应力σ1的求解变化,其余各档应力σ2至σ5也相应变化。与常规“扫描试凑算法”每计算一点不平衡张力需上万次或十几万次迭代相比,“扫描二分法”只需要几十次,更适用于工程设计中杆塔逐基批量计算。
1.3 计算结果示例
采用上述算法求得各档应力后,即可计算相邻档间不平衡张力和各档脱冰后弧垂。选取JL/G1A-500/65 钢芯铝绞线导线,覆冰厚度为20 mm,脱冰率为80%[13-15],连续5 档。一档脱冰指中间第3 档脱冰,各档弧垂曲线如图4(a)所示,最大不平衡张力发生在第3、4 基铁塔上;一侧脱冰指第1、2 档不脱冰,第3、4、5 档脱冰,各档弧垂曲线如图4(b)所示,最大不平衡张力发生在第3 基铁塔上。
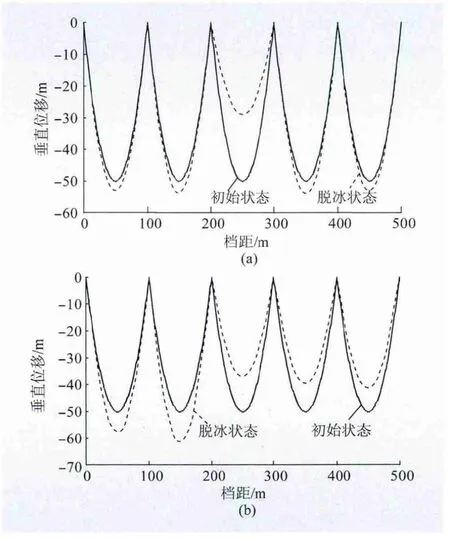
图4 脱冰后弧垂曲线Fig.4 Ice-shedding sag curves
2 连续档不平衡张力的敏感性分析
2.1 计算条件
以2013—2014年度设计并施工的浙北—福州1 000 kV交流线路工程为例,计算条件如下。
(1)气象条件:覆冰厚度越大,发生不均匀脱冰时不平衡张力也越大,该工程设计覆冰厚度为10 ~30 mm,本文取覆冰厚度为20 mm 代表性计算。
(2)导线:覆冰为20 mm 时,推荐导线JL/G1A-500/65 钢芯铝绞线,每相导线采用8 分裂。
(3)绝缘子:覆冰为20 mm 时悬垂串采用盘式绝缘子,通常计算串长取12 m。
(4)脱冰率和档距组合:按照重覆冰区杆塔荷载设计原则[13-15],直线塔脱冰率取80%,并取连续5 档;一档脱冰指中间第3 档脱冰,其余档不脱冰;一侧脱冰指1、2档不脱冰,3、4、5 档脱冰。通常计算档距取500 m。
2.2 绝缘子串长的敏感性分析
悬垂绝缘子串长会对导线不均匀脱冰时的不平衡张力产生影响,如串长很短,接近于固定点悬挂方式,相邻档间的耦合较小,不平衡张力较大;如串长很长,悬挂点发生同样的纵向偏移时,其垂直位移抬升,因而不平衡张力减小,如图5 所示。图中导线不平衡张力百分比指导线不平衡张力与最大使用张力的比值。
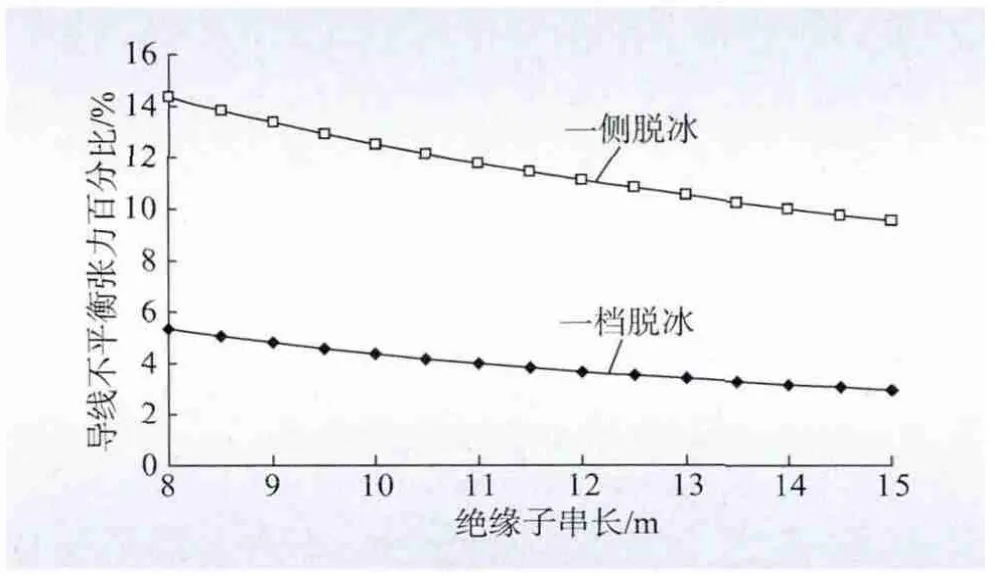
图5 悬垂绝缘子串长的敏感性分析图Fig.5 Sensitivity analysis curves of suspension strings' length
2.3 导线型号的敏感性分析
取连续5 档计算,非脱冰档各档档距均为500 m,而中间第3 档脱冰档档距取500 ~1 000 m,选取G1A 普通强度钢线和G2A 高强度钢线作比较,选取35、45、65 不同钢截面作比较,如图6 所示。结果表明,导线刚度越大,其不平衡张力越小。
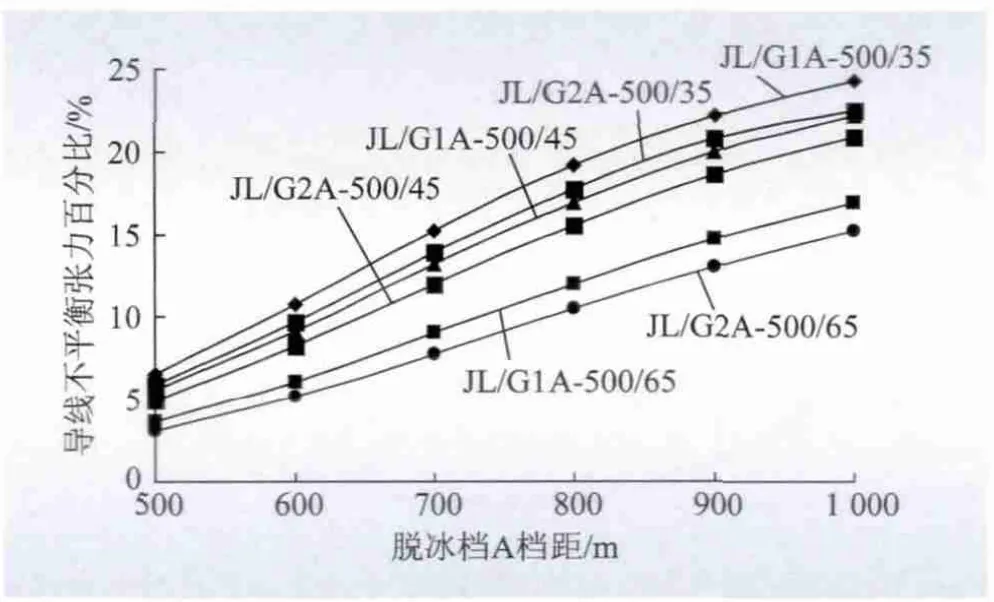
图6 导线型式的敏感性分析图Fig.6 Sensitivity analysis curves of conductor types
2.4 连续档距组合的敏感性分析
因为一个耐张段内各档导线通过直线塔悬垂串相互关联耦合,因而导线脱冰动力过程不仅由脱冰档参数决定,同时相邻档导线的相关因素也会对其有影响。本节考虑连续档距组合,主要包括以下因素:脱冰档档距、连续档数及脱冰档在连续档中的位置。计算中采用的档距组合如表1 所示,耐张段两端采用耐张塔,而中间均为直线塔。非脱冰档B 档距取500 m,而脱冰档A 档距取500 ~1 000 m,其余计算条件不变,各种组合下的计算结果如图7 所示。

表1 不同的档距组合配置Tab.1 Different multi-span configurations
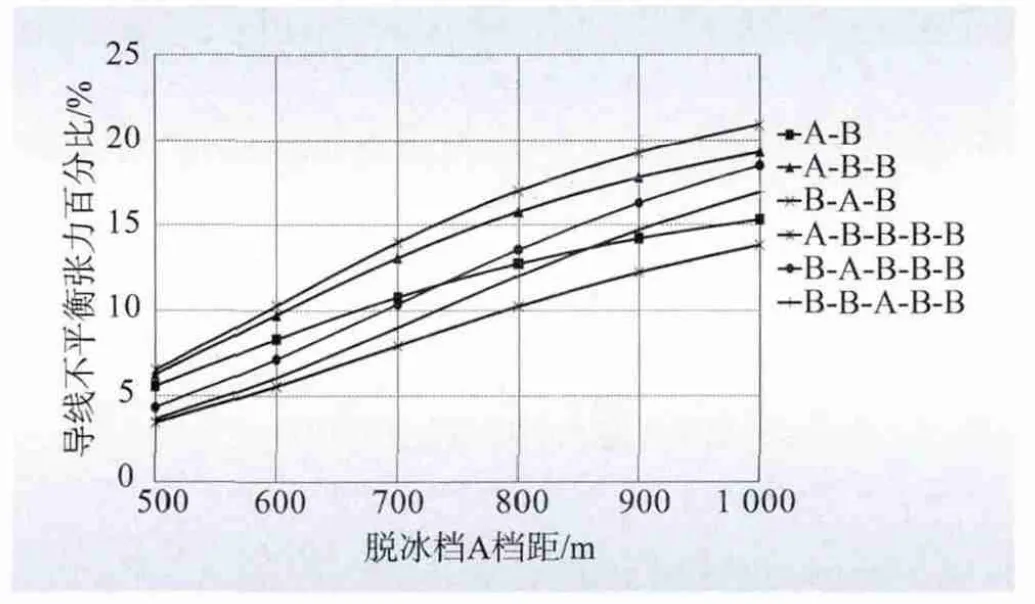
图7 不同档距组合的敏感性分析图Fig.7 Sensitivity analysis curves of different multi-span configurations
结果表明,档距组合对不平衡张力的影响显著。脱冰档两侧的连续档数越多、档距越长,则悬挂点处的档间耦合越强,因而不平衡张力越大。但随脱冰档档距的增大,各种组合条件下的不平衡张力呈现饱和趋势。
2.5 大小档及高差的敏感性分析
针对山区线路常出现大小档及大高差的情况,本节取连续5 档C-C-A-B-C,对不平衡张力计算分析。大小档计算设定条件:档距取500 m,相邻档A 与B 档距之和设定为1 000 m,按照A 与B 比值取0.2 ~5 来分配A和B 档距而形成大小档。一档A 脱冰和一侧A、B、C 档脱冰时计算不平衡张力的结果如图8 所示。结果表明,当大小档A 与B 比值小于2.5 时,其对不平衡张力有一定影响,大于2.5 时,不平衡张力呈现饱和趋势。
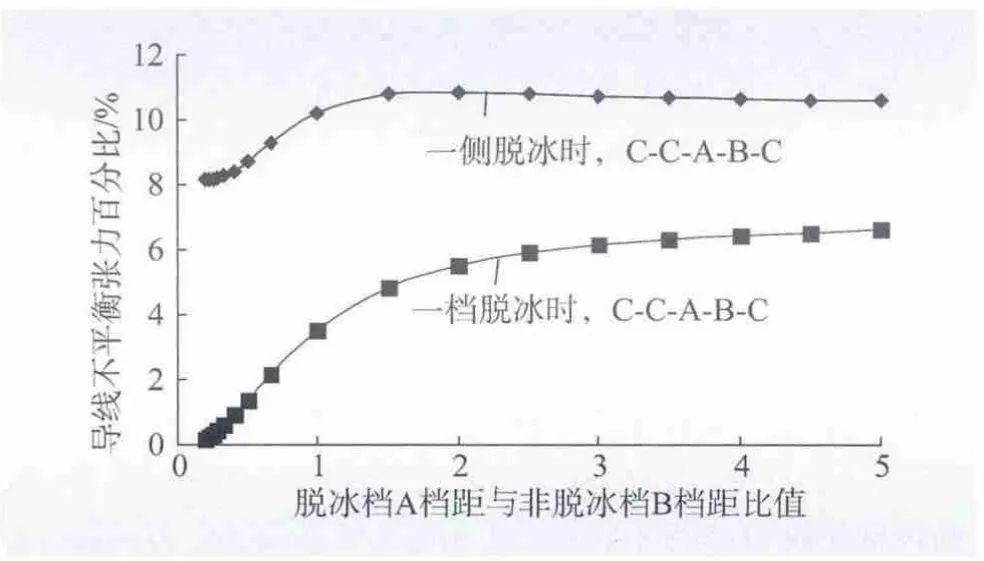
图8 大小档敏感性分析图Fig.8 Sensitivity analysis curves of large-small span
取连续5 档C-C-A-B-C 计算,高差计算设定条件:A 和B 档距均取500 m,A 档大小号侧杆塔挂线点高差取0 ~300 m,一档A 脱冰和一侧A、B、C 档脱冰时不同高差下计算不平衡张力结果如图9 所示。结果表明,A 档大小号侧杆塔挂线点高差对不平衡张力影响小,可忽略不计。
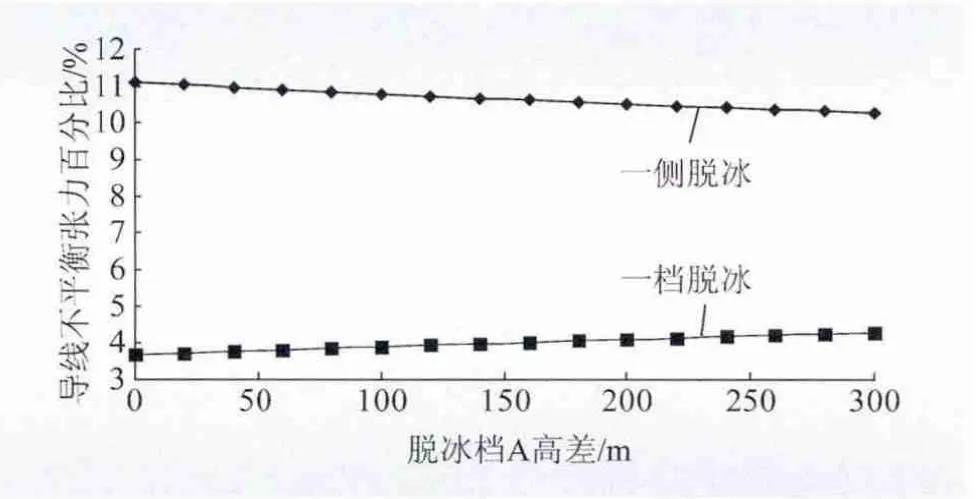
图9 高差的敏感性分析图Fig.9 Sensitivity analysis curves of elevation difference
2.6 脱冰率的敏感性分析
脱冰率越大,导线不平衡张力也越大。本节考虑相同计算条件下,仅改变脱冰率(以初始冰载荷的百分比计),得到脱冰率与不平衡张力的关系,如图10所示。二者近似满足线性关系,随着脱冰率增大,导线不平衡张力也增大。
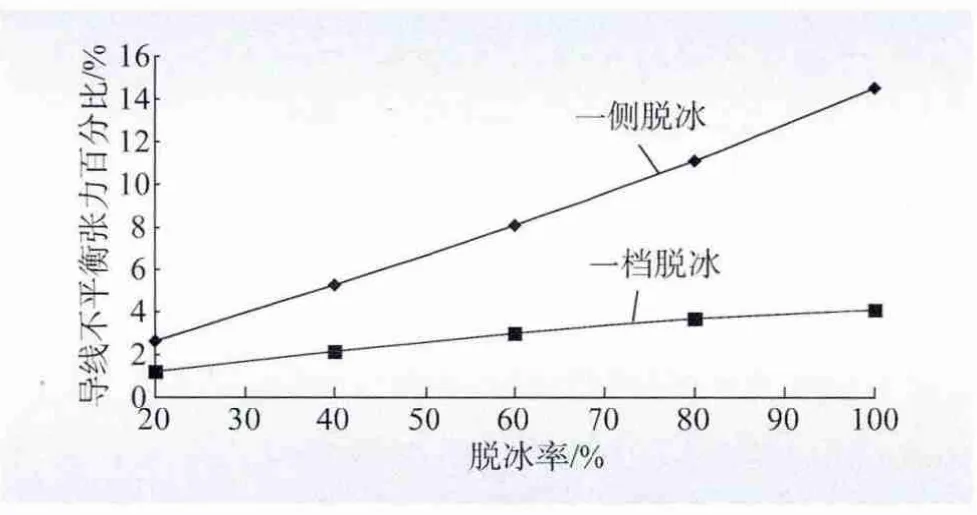
图10 脱冰率敏感性分析图Fig.10 Sensitivity analysis curves of ice-shedding percentage
3 孤立档不平衡张力的敏感性分析
3.1 孤立档不平衡张力的特殊性
耐张塔与耐张塔相邻的单独孤立档和连续档相比具有以下特殊性:(1)导线张力控制工况不同导致耐张塔两侧张力差较大,重覆冰区连续档侧线路多为最大荷载控制,而孤立档侧线路多为过牵引控制;(2)两侧代表档距不同导致耐张塔两侧张力差较大。综上,耐张塔两侧不平衡张力本身就较大,不均匀脱冰使其不平衡张力值更大,如图11 所示。孤立档档距取100 ~600 m,按照重覆冰区杆塔荷载设计原则[13-15],耐张塔一侧脱冰率取100%,不平衡张力值随孤立档档距增加而减小,在500 m 附近出现拐点。
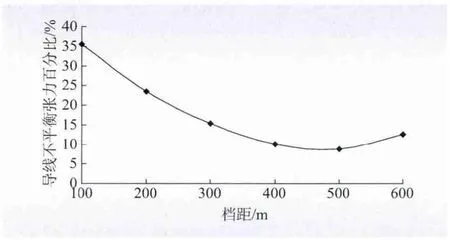
图11 孤立档敏感性分析图Fig.11 Sensitivity analysis curve of isolated span
3.2 引入不均匀脱冰模式
工程设计中为计算方便,对不均匀脱冰进行校验时通常简化为如图12(b)所示的均匀脱冰。然而实际情况下导线脱冰具有随机性,图12(c)所示的不均匀脱冰情况也有可能发生。

图12 导线均匀和不均匀脱冰模式Fig.12 Uniform and uneven ice-shedding of conductor
架空导线悬链结构中,靠近悬挂点位置导线刚度较大,而档距中点位置刚度最小。因此当脱冰发生在沿档距方向的不同位置时,即使脱冰率相同,引起的不平衡张力也会不同。考虑到耐张塔作为耐张段承力塔的重要性,对孤立档进行不均匀脱冰模式下的不平衡张力计算[9],各档档距取500 m,如图13 所示。结果表明,相同脱冰率下,不均匀脱冰时,越靠近档距中央,其不平衡张力越大,且明显大于均匀脱冰时的情况。
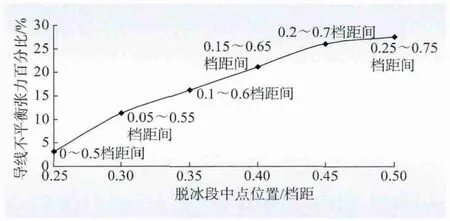
图13 不均匀脱冰模式敏感性分析图Fig.13 Sensitivity analysis curve of uneven ice-shedding
4 结 论
(1)采用“等线长法”计算模型,引入“扫描二分法”改进迭代算法,可实现逐塔的不平衡张力计算,适用于工程设计,效率高、误差小。
(2)导线发生不均匀脱冰时,导线、绝缘子串同步振动,绝缘子串越长,其最大偏转角较小,直线塔悬挂点处纵向不平衡张力随之减小。设计时通过加长串长可削弱不平衡张力的影响。
(3)导线刚度越大,不平衡张力越小。设计时通过选取高强度导线可削弱不平衡张力的影响。
(4)档距组合对不平衡张力影响显著,脱冰档两侧的连续档数越多、档距越长,不平衡张力越大,且随脱冰档档距增大呈现饱和趋势;山区大小档比值小于2.5 时,对不平衡张力有一定影响,大于2.5 时,不平衡张力呈现饱和趋势;山区高差对不平衡张力影响较小,可忽略不计。在重覆冰区选线设计时,调整档距配置可削弱不平衡张力的影响。
(5)导线不均匀脱冰不平衡张力与脱冰率成线性关系。设计时可根据当地实际情况考虑不平衡张力值,选择更为合适的脱冰率,做到安全可靠。
(6)设计时需对具有特殊性的孤立档进行单独的不平衡张力计算,考虑到耐张塔作为承力塔的重要性,建议设计耐张塔时考虑非均匀脱冰模式下的不平衡张力值。
[1]陆佳政,彭继文,张红先,等.2008年湖南电网冰灾气象成因分析[J].电力建设,2009,30(6):29-32.
[2]蒋兴良,马俊,王少华,等.输电线路冰害事故及原因分析[J]. 中国电力,2005,38(11):27-30.
[3]张子引,刘学军.架空输电线路连续档不平衡张力计算[J]. 电力建设,2009,30(5):32-34.
[4]侯镭,王黎明,朱普轩,等.特高压线路覆冰脱落跳跃的动力计算[J].中国电机工程学报,2008,28(6):1-6.
[5]Jamaleddine A,McClure G,Rousselet J,et al. Simulation of iceshedding on electrical transmission lines using ADINA [J].Computers and Structures,1993,47(4-5):523-536.
[6]Fekr M R,Mcclure G.Numerical modelling of the dynamic response of ice-shedding on electrical transmission lines [C]//7th International Workshop on Atmospheric Icing of Structures,Que.,Canada,1996.
[7]Kalman T,Farzaneh M,McClure G. Numerical analysis of the dynamic effects of shock-load-induced ice shedding on overhead ground wires[J]. Computers and Structures,2007,85(7 - 8):375-384.
[8]张殿生,倪宗德,张洞明,等. 电力工程高压送电线路设计手册[M].2 版.北京:中国电力出版社,2003:202-205.
[9]邵天晓.架空送电线路的电线力学计算[M].2 版. 北京:中国电力出版社,2003.
[10]徐士良,马尔妮.常用算法程序集(C/C + +描述)[M].5 版. 北京:清华大学出版社,2013:172-173.
[11]杨克昌.计算机常用算法与程序设计案例教程[M]. 北京:清华大学出版社,2011:85-87.
[12]徐士良,谭浩强,林定基,等.计算机常用算法[M].2 版.北京:清华大学出版社,1995:149-151.
[13]DL/T 5440—2009 重覆冰架空输电线路设计技术规程[S]. 北京:中国电力出版社,2009:20-21.
[14]GB 50665—2011 1 000 kV 架空输电线路设计规范[S].北京:中国计划出版社,2011:23-25.
[15]GB 50545—2010 110 kV ~750 kV 架空输电线路设计规范[S].北京:中国计划出版社,2010:27-30.
