基于单元体剪切面的坑中坑基坑临界间距判别方法

2014-02-13霍军帅周顺华

都市快轨交通 2014年5期

霍军帅周顺华

(1.成都地铁有限责任公司成都610041;2.同济大学道路与交通工程教育部重点实验室上海201804)

1 研究背景

随着我国城市化水平不断提高，城市当中出现了大型商场、地下综合体、交通枢纽等不同类型的基坑工程。当以上类型的基坑工程受到建(构)筑物形式、周边地块同期开发以及多种构筑物共同体的建设等影响，为了满足购物、换乘、接驳等使用功能要求而采取一体化施工时，就导致了深大异形、坑中坑基坑工程的出现［1］。

通俗来讲，坑中坑基坑就是在一个大基坑(外坑)开挖到设计标高后再落深开挖一个小基坑(内坑)，最终开挖形成的基坑，这里的大小(或内外)是相对于位置而言的。坑中坑基坑的断面形式如图1所示。

图1 坑中坑基坑剖面

坑中坑基坑由于内坑的存在，给基坑的围护结构设计、施工开挖和环境保护带来了难度，若考虑不周全可能会酿成重大工程事故。以往，由于内坑的规模较小，基坑围护设计不考虑内坑的影响并未出现较大的工程事故，造成人们对坑中坑基坑的重视程度不够［2］。但是，近年来随着内坑规模、数量的增大，若仍然采用以往的计算模式来控制基坑的稳定，必然会导致一些基坑工程事故的发生［3］。

坑中坑基坑开挖的力学特征可以概括为对中间土体的外坑开挖竖向卸载(图2(b))和内坑开挖侧向卸载(图2(c))，存在着对内、外坑围护结构间中间土体的双向开挖应力释放问题［1，4，5］。因此，与单一基坑不同，坑中坑基坑除了考虑外坑开挖卸载对外坑围护结构稳定和变形的影响，还需兼顾内坑开挖卸载造成的内、外坑围护结构之间稳定和变形的循环加剧影响。

根据工程常识，基坑开挖的变形影响范围是有限的，内、外坑围护结构之间应该存在一个开挖相互影响的临界间距，内、外坑围护结构间距近则考虑开挖的相互影响，远则近似忽略开挖的相互影响。确定内、外坑开挖影响的临界间距时需要先界定基坑开挖的影响范围，而对于基坑开挖的影响范围，往往根据工程特点，结合工程经验假定基坑开挖的破坏面形式进行设计和施工。

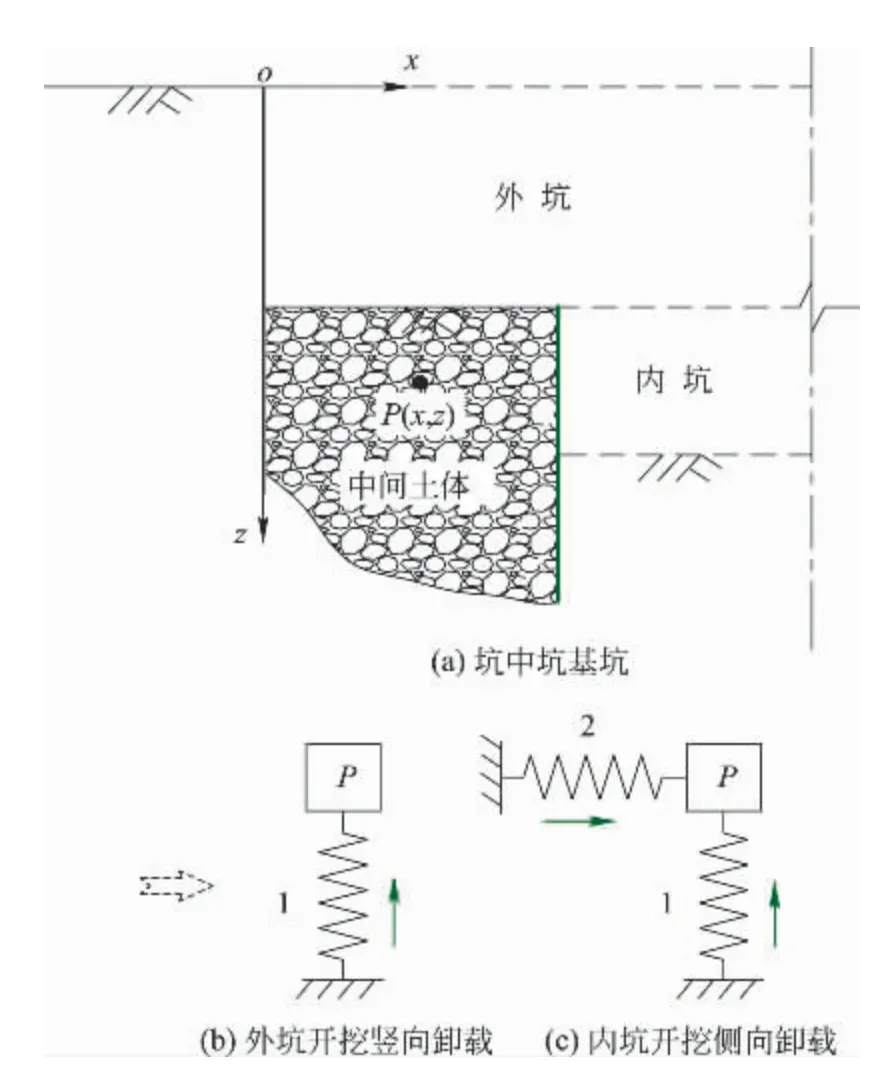
图2 坑中坑基坑开挖力学特征［4］

2 现行规范给出的破坏面形式

现行规范［6-7］给出了基坑开挖完成后基底不同类型的抗隆起稳定分析滑动面。

《基坑工程技术规范》在验算基坑坑底抗隆起稳定性时给出了两种验算模式，即一种是考虑了墙体的弯曲能力，另一种是考虑了墙底土体的塑性涌入。两种模式如图3所示。

若按图3(a)的模式分析，以地下连续墙的插入深度为半径采用圆弧滑动面形式，则由此确定的坑中坑基坑开挖相互影响的地连墙临界间距(分别为外坑、内坑地下连续墙插入深度)如图4(a)所示。

若按图3(b)的模式分析，墙底采用对数螺旋线加直线的滑动面形式，则坑中坑基坑开挖相互影响的地连墙临界间距lc可计算得出，如图4(b)所示。

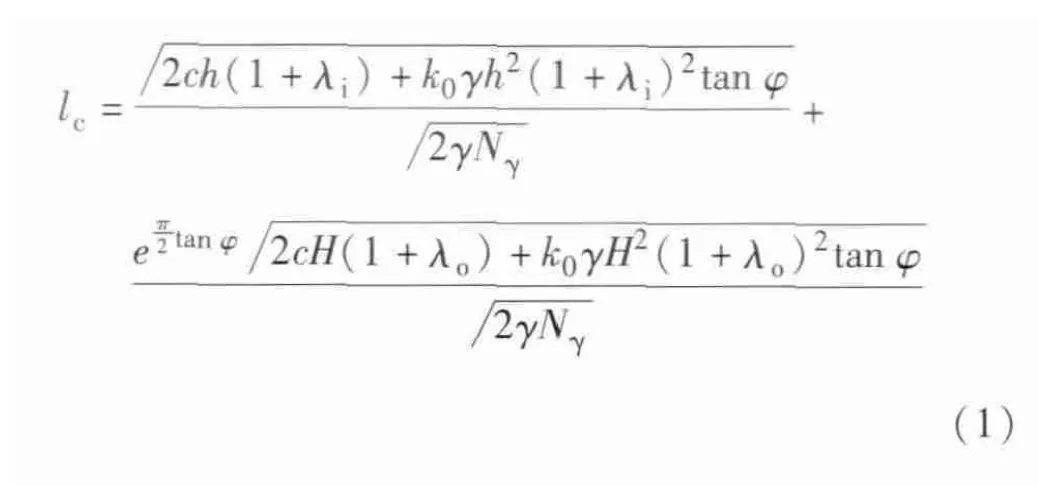
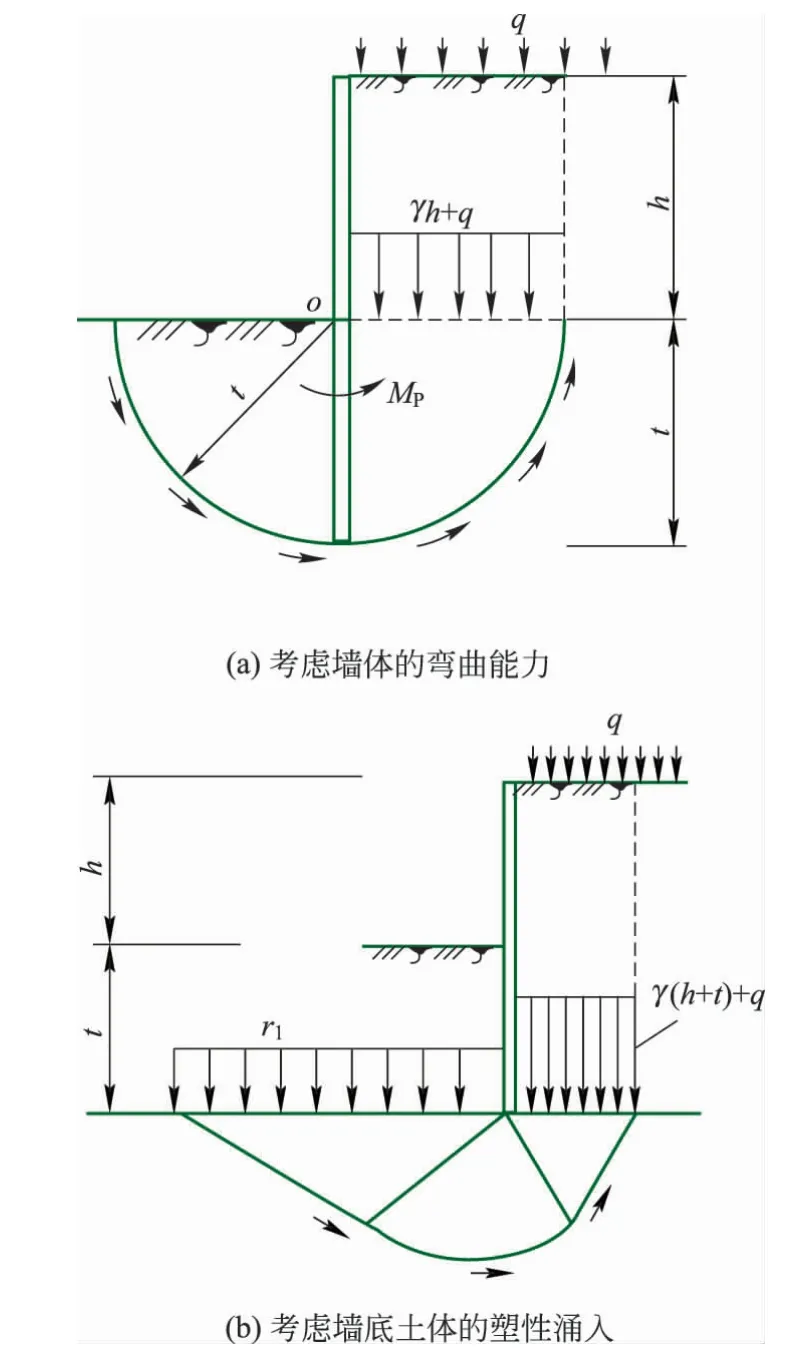
图3 基坑基底抗隆起稳定性验算图式［6］

图4 不同滑动面形式确定的坑中坑基坑临界间距

式中，c，φ为土的强度指标;γ为土的容重;λi，λo为内坑、外坑地连墙插入比;h，H为内坑、外坑开挖深度;k0为静止侧压力系数;Nγ为地基土承载力系数，与φ有关。

显然，该临界间距与土性、基坑开挖深度及地下连续墙插入比有关。

从以上分析可知，若以规范给出的破坏面形式来判定坑中坑基坑临界间距，是基于将内、外坑分别视作单一基坑为前提的，其适用性有待商榷。

3 基于单元体试验剪切面形式的破坏面

根据室内单元体试验的研究成果，土体在外力作用下是沿着某一剪切面发生剪切破坏的，该剪切面与大主应力作用面的夹角为45°+φ/2，如图5所示。

图5 单元体加载试验

基坑开挖时，坑底被动区土体的受力性状与单元体受压时性状类似，被动区土体的水平向应力(被动土压力)为大主应力，被动区土体受围护结构挤压按单元体剪切面形式破坏，破坏面与竖直面的夹角为45°+φ/2。因此，若知道了被动土压力的计算深度，就可以计算出被动区土体破坏面的水平向投影长度，进而可确定坑中坑基坑内、外坑开挖影响的临界间距。

对于基坑被动土压力的计算深度，按照朗肯土压力理论从开挖面算起，没有考虑围护墙的变形。对围护墙进行内力分析时，等值梁法考虑了围护墙的变形，认为对于有支撑或有锚杆的围护结构的变形曲线存在一反弯点，且在反弯点处的弯矩为零，如此一来可以把围护结构划分为两段假想梁，上部为简支梁，下部为一次超静定梁，如图6所示。

对于假想铰位置，有几种不同的理论和假定:1)假定土压力为零处为假想铰位置;2)假定基坑开挖面处为假想铰位置;3)假定假想铰距离基坑开挖面以下y距离处，y值由地质条件及围护结构特性决定。文献［8］按第3种假定，给出了多支撑基坑围护结构假想铰位置y的参考取值，如表1所示。

图6 等值梁法基本假定

表1 多支撑基坑围护结构假想铰位置

根据上海地区的经验，一般y=(0.1～0.2)H。若采用单元体剪切面形式，被动区土体的计算深度按等值梁法选取，则可计算出坑中坑基坑内、外坑开挖相互影响的临界围护墙水平距离lc(见图7)，有

式中，D为外坑围护墙的插入深度，φ为外坑坑底土体的有效内摩擦角。

需要说明的是，图7和式(2)中的lc是基于基坑围护墙的最佳插入深度D确定的，即当外坑围护墙插入深度达到一定值时，再增加围护墙插入深度对控制围护墙变形的贡献并不增加，此时的围护墙插入深度便为最佳插入深度，lc的计算不计多余深度的影响。根据上海地区的经验，上海深基坑工程的最佳插入深度为0.9～1.0倍的开挖深度。

图7 单元体剪切面形式确定的内、外坑临界间距

4 临界间距离心模型试验验证

4.1 离心模型试验原理

离心模型试验是根据相似理论，用离心机的惯性离心力来模拟自重效应，对相对原形缩小了n倍(n为模型率)的模型施加n倍重力加速度而进行的试验。根据近代相对论的解释，牛顿的重力与惯性力是等效的，故原形在地球上受到的重力与模型在离心机上受到的离心力所产生的物理效应是一致的。由于惯性力与重力等效，且工程材料性质未变，从而使模型与原形的应力应变相等、变形相似、破坏机理相同，能再现原形特性［9-11］。

4.2 试验概况

4.2.1 试验方案

既有的研究成果表明，当基坑围护结构采用地下连续墙形式时，在保证墙体有足够强度和刚度的条件下，恰当增加插入深度可以提高抗隆起稳定性。但对于有内支撑的围护墙，按上海地区的工程实践经验，当地下连续墙插入深度＞0.9H(开挖深度)时，其效果不明显［8，12］。因此，从试验目的出发，为更好地获得内、外坑开挖的相互影响，试验时将内、外坑地下连续墙的插入比均取为1∶1。

为了尽量消除离心模型试验模型箱的边界效应，同时又能得到预期的试验效果，试验时外坑开挖深度为8 m(分2层开挖)，内坑开挖深度为5 m(1层开挖)。

为模拟内、外坑开挖的相互影响，试验时固定外坑的开挖宽度、深度及内坑的开挖深度，而改变内、外坑地下连续墙之间的距离，即改变中间土体的宽度，进而观察开挖对内、外坑围护结构变形的影响，试验方案见表2。

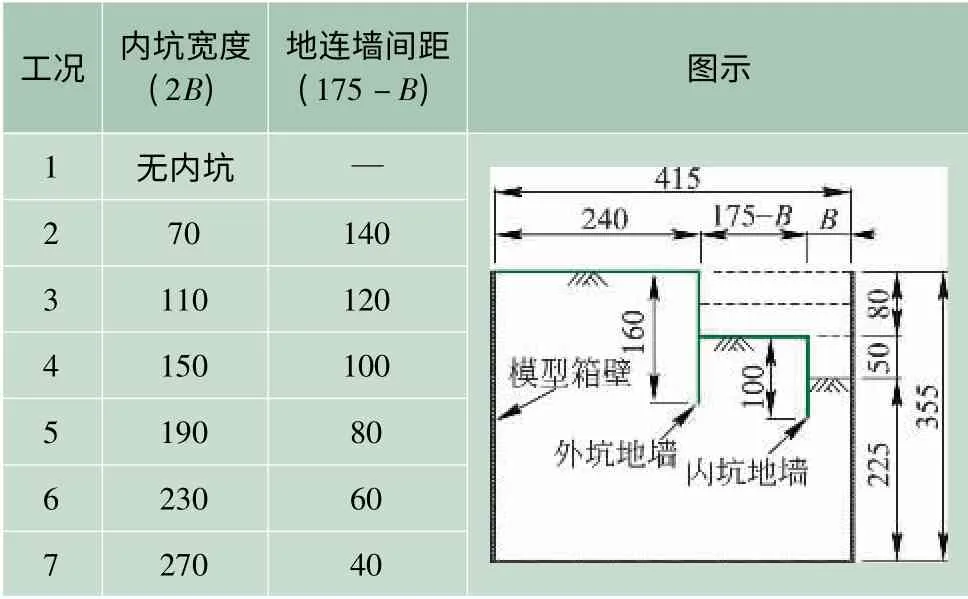
表2 坑中坑基坑离心机试验方案 mm

4.2.2 试验设备

离心模型试验采用的是同济大学的L-30型离心机，该机的主要性能参数见文献［1］。根据试验设计的目的、模型箱的实际尺寸、离心试验的边界效应，并结合同济大学L-30土工离心试验机的工作条件，试验选取的模型率n为100，即试验过程中离心机运转的加速度为100 g。

4.2.3 试验用土

因试验工况较多，为减少固结时间、缩短试验周期，试验用土取自研究所依托上海地铁工程的⑦1层砂质粉土，土层的主要物理力学指标见表3。

表3 试验用土土层参数

4.2.4 试验辅助材料

1)地下连续墙替代材料。根据地下连续墙的受力和变形特点，做离心机试验时可以用铝板作为替代材料，根据相似理论替代材料应该与原形材料抗弯刚度相似的原则，有

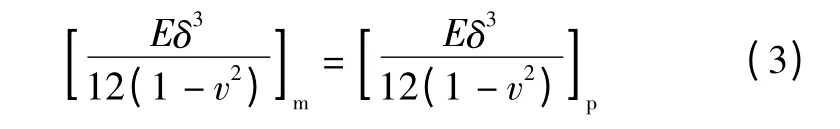
式中:m代表模型材料，p代表原型材料，则根据弹性模型材料的常用相似关系［13］有vm=vp，Em=Ep=σp/εp，δm=δp/n，n为模型率。

2)混凝土支撑替代材料。为了验证试验的可实施性，混凝土支撑采用紫铜管模拟。同样根据相似理论，按照抗压刚度等效的原则，有

式中各符号意义同式(3)。

经过计算，用厚度为5.8 mm铝板来模拟0.8 m厚的地下连续墙(内、外坑)，用直径5 mm、壁厚2 mm的紫铜管来模拟规格为0.8 m×0.8 m的混凝土支撑。

4.2.5 试验过程

1)试样制备。上海的⑦1层砂质粉土层为承压含水层，含水量较高，在做离心机试验时，试样制备面临着含水量控制的问题，加上本试验工况较多，所以对试样含水量更为严格。对于含水量的控制，本试验以时间作为控制参数，即将土样充分搅拌均匀后，装满模拟箱，再放入离心机内进行固结。

2)开挖过程。基坑的开挖和试验制备一样，同样以时间作为控制参数。借鉴实际工程的开挖时间，开挖类似外坑一层土用时在30 d左右，根据相似原理，开挖模拟时间控制在4 min。

3)施加支撑。试样制备前，在模型箱的右侧壁内侧精确定位，设置支撑支点装置，先撑后挖。

4)试验数据采集。试样在模型箱内制作完成后，在试样的前侧面按设定的间距布置光标点阵，然后加盖涂有凡士林的透明有机玻璃板，最后将模型箱放入离心机仓内进行试验操作。在试验过程中，通过定点高速同步摄像系统对不同试验阶段的光标点阵成像，后期再通过计算机图形处理软件，分析光标的坐标变化情况。因光标的位移与土体的位移同步，进而可以分析土体的位移变化情况。

4.3 试验结果

试验时通过同步摄像系统对模型在试验中的全过程进行监控，并拍摄模型照片，地下连续墙间距为12 m时的试验照片见图8。因其他两组试验的试验过程与此一致，在此不再重复。

外坑地下连续墙最大水平位移随地连墙间距的变化如图9所示。

图8 地下连续墙间距为12 m时的试验结果

图9 不同开挖工况下外坑地连墙最大水平位移随地连墙间距的变化曲线

由图9可以看出，不同开挖步随着内、外坑地下连续墙间距的增大，外坑地连墙最大水平位移呈现出先减小后增大最后趋于平缓的趋势。表明:坑中坑开挖时，内坑地下连续墙起到了外坑坑底加固体的作用，有效地阻挡了外坑地下连续墙水平位移的发展。但是，这种阻挡效果发挥的优劣与内、外坑地下连续墙间距有关，即与中间土体的宽度有关。当地下连续墙间距为8～12 m时，阻挡效果明显;当地下连续墙间距大于14 m时，阻挡效果趋于稳定，此时可以忽略内、外坑开挖的相互影响。

内坑地下连续墙最大水平位移随地连墙间距的变化如图10所示。

与外坑相同，不同开挖步随着内、外坑地下连续墙间距的增大，内坑地连墙最大水平位移呈现出先减小后增大最后趋于平缓的趋势，只是内坑的这种趋势更为明显。