轨道交通客流预测的扩展反馈四阶段法研究

肖 颖 刘晓建

(重庆金美通信有限责任公司 重庆400030)

城市轨道交通是支持城市交通发展及优化城市空间布局的重要基础建设，对城市轨道交通进行工程可行性分析的一个重要前提是对客流进行准确的预测［1］。一套完整、科学、准确的客流预测数据是城市轨道交通规划方案设计中不可或缺的重要依据。目前在轨道交通线路客流预测的方法中应用较多的是四阶段法［2］。该方法以城市总体客流预测、分布及线网流量和交通方式为基础，既从宏观上研究交通系统的总体客流，又从微观上深入研究轨道交通线路的客流情况。由于此方法对当今轨道交通的复杂度分析不够，各阶段相对独立导致预测的客流量大于实际客流量。基于传统的四阶段客流预测方法，笔者提出了“扩展四阶段客流预测方法”。该方法在交通产生、交通分布、交通方式划分和交通分配4个阶段的总体框架下，增加了“时段划分”和“反馈”修正。

1 扩展四阶段法概述

传统四阶段法是将客流预测过程分为4步:交通产生、交通分布、交通方式划分和交通分配，其工作流程如图1(a)所示。

交通产生是通过现状年发生与吸引交通量和社会经济与土地利用基础数据来预测未来年的发生与吸引交通量;交通分布是通过区间的费用矩阵预测未来年各区间的出行分布量;交通方式划分则是利用预测的未来区间的全方式交通分布量划分为分方式的分布量［3］;交通分配是将交通方式分布量分配到交通线网中，预测各路段的交通量。笔者提出的扩展四阶段法示意如图1(b)所示。扩展四阶段客流预测方法相比传统的四阶段法，在交通方式划分阶段之后增加了交通时段划分，并且增加了反馈修正过程。

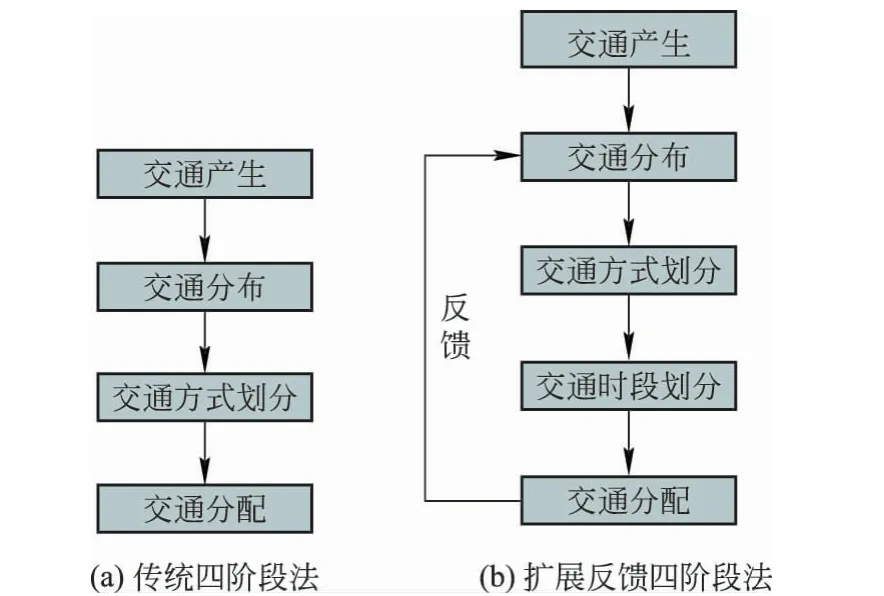
图1 四阶段法步骤

2 扩展四阶段法预测过程

2.1 交通产生

交通产生包括出行产生和出行吸引。前者以出行者的社会经济特征为主，与其出行强度关系最大;后者以土地利用的布局为重，与土地利用的性质和开发程度相关［3］。按照出行发生和吸引率预测小区的出行产生Gi和出行吸引Ai，表示为

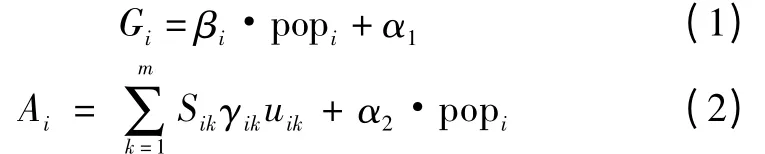
式中:Gi、Ai分别是交通小区i的产生量和吸引量;popi是小区i的预测人口数;βi是小区i的平均出行概率;Sik、γik和uik分别是小区i第k类用地的面积、开发强度和单位建筑面积的出行吸引率;m是小区i的总用地类型;α1和α2为偏回归系数。

2.2 交通分布

在交通分布中，多应用双约束重力模型，对全方式出行进行分布预测［4］。该模型假设:交通小区i、j之间的分布交通量，与小区i的产生交通量及小区j的吸引交通量成正比，而与两小区之间的交通阻抗成反比。出行量Tij可以表示为

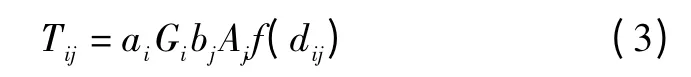
式中:Tij(i、j=1，2，3…)是交通小区i到交通小区j的出行量是模型平衡系数;f(dij)是交通阻抗函数，该函数一般为负指数形式，f(dij)=，其中t＞0，dij是交通小区i和交通小区j之间的最小效用(出行距离或者时间)。

2.3 交通方式划分

交通方式的多样化增加了交通方式划分的复杂度。一般的多项离散选择方法(multinomial logit，MNL)由于有不相关替选方案独立性(independence of irrelevant alternatives，ⅡA)的理论缺陷，会产生“红蓝公交”问题，无法适应方式细分后的方式划分，因此须采用嵌套式离散选择方法(nested logit model)。该方法将特性类似的交通方式组合成类，各类按相似性多次组合，由此形成树状的分类树，如图2所示，然后通过条件概率，实现先大类后小类的方式选择，从而避免了多项离散选择方法的不相关替选方案独立性缺陷。

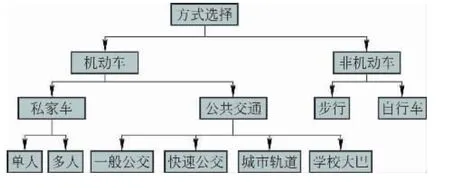
图2 交通方式结构

轨道交通和地面常规公交两种交通方式出行效用差，考虑步行到站时间、步行出站时间、等车时间、车内时间、换乘时间、换乘次数的影响，建立Logit公交子方式划分模型［5］，预测轨道交通出行矩阵，轨道交通出行概率Pmetro表示为

式中

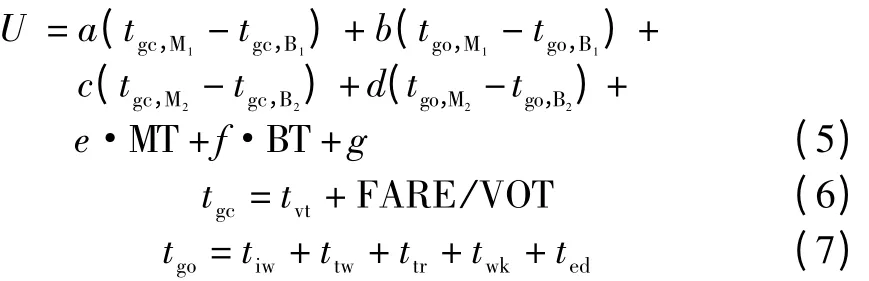
其中:U是出行效用差;tgc是车内广义时间;tgo是车外广义时间;M1表示步行到轨道交通站、出站后步行到达目的地、出行过程中没有使用常规公交;B1表示出行过程中没有使用轨道交通，仅使用一次常规公交;M2表示出行过程中通过常规公交换乘轨道交通;B2表示出行过程中没有使用轨道交通、但使用两次或者两次以上常规公交;tgc，M1表示M1方式下的车内广义时间;tvt是车内时间，tiw是初始等车时间，ttw是换乘等车时间，ttr是换乘时间，twk是步行到车站的时间，ted是出站后到达目的地所用时间;FARE为票价，VOT为时间价值;MT为轨道交通出行换乘次数，BT为公交出行换乘次数;a～g为变量系数。

2.4 交通时段划分

利用时间序列分析方法，预测未来阶段的客流量，在此基础上，将客流量划分为若干个时间节点［6］。交通线路客流的时段分布是线路客流在全日各个时间段上的流量大小分布。轨道交通中常用的时间段大小为15 min［7］。

2.5 交通分配及反馈修正

交通分配是将已经预测的起讫点之间的出行分布数据(OD矩阵)按照一定的准则分配到线网中的各条路段上，并且求出各条路段上的交通流量。交通分配模型包括道路网络机动车交通分配模型和公交网络轨道交通客流分配模型［8］。

根据交通分配模型得到的交通流量，对路段通行时间进行更新，并且改变交通分布模型中的各OD对之间的最小效用，并以此重新计算交通分布=aiGibj。根据两次OD矩阵的相似度，判断是否收敛。收敛准则采用总方差根法(Root Squared Error，RSE)，其计算公式［9］为

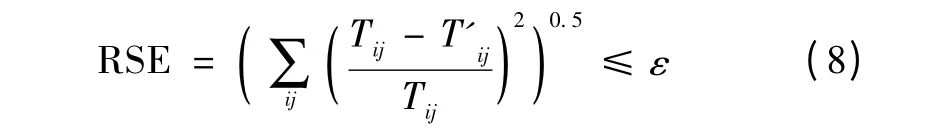
式中:ε为用户设置的反馈收敛精度目标，当ε不满足上式时，需要对OD结果进行修正，采用连续平均法(methodof successive averages，MSA)，将前后两次出行分布的结果进行加权平均，权重随迭代次数的增加而减少［9］。

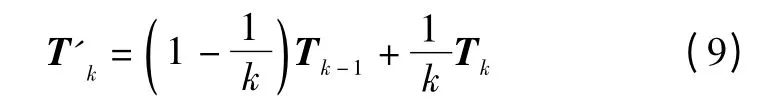
式中:T＇k是调整后的k次循环出行矩阵;k是循环次数;Tk-1是k-1次循环所用的出行矩阵;Tk是k次循环重力模型得到的出行矩阵。

3 模型应用

3.1 重庆轨道交通概况

重庆轨道交通网目前主要由4条线路构成，线路总长173.4 km，设置车站115座，详细数据如表1所示。

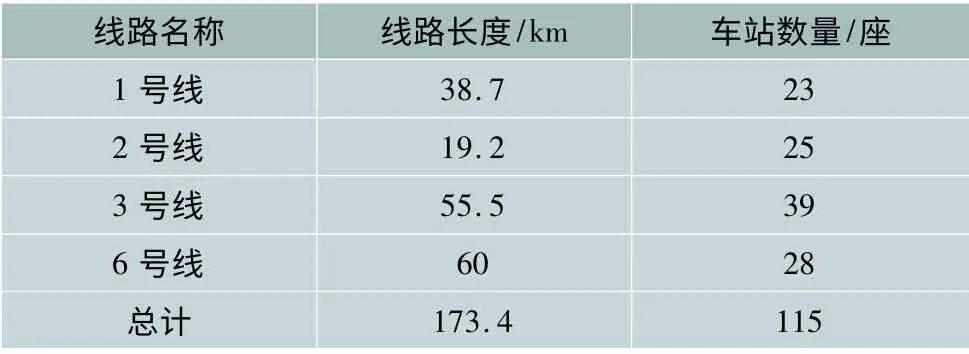
表1 重庆轨道交通现状

以重庆轨道交通3号线为研究范围。重庆轨道交通3号线南起鱼洞，北至江北机场及江北环城北路，全长约55.5 km，为南北方向的轨道交通骨干线，共设车站39座，其中换乘站4座。该线路横跨巴南、南岸、渝中、江北、渝北5区，并与江北机场、2个火车站(菜园坝站和重庆北站)、4个长途汽车站(南坪、菜园坝、红旗河沟和江北客站)对接，成为重庆南北方向交通的主动脉。

重庆轨道交通票制采用里程制，起步价为2元，最高为7元，表2为重庆轨道交通票价方案。

表2 重庆轨道交通票价方案

3.2 重庆轨道交通3号线客流预测方法

应用扩展四阶段法，结合具体内容，形成重庆轨道交通3号线客流预测流程，如图3所示。

3.3 预测结果分析

根据上述模型结构和预测流程，采用扩展反馈四阶段法对重庆轨道交通3号线客流进行预测，图4为预测客流相对误差与迭代次数的关系。若式(8)中的ε=5%，3个目标年2015、2025和2035年迭代次数分别为7、8和9次时，扩展反馈四阶段法即可收敛。同时随着预测的年份越远，则收敛需要的迭代次数越多。

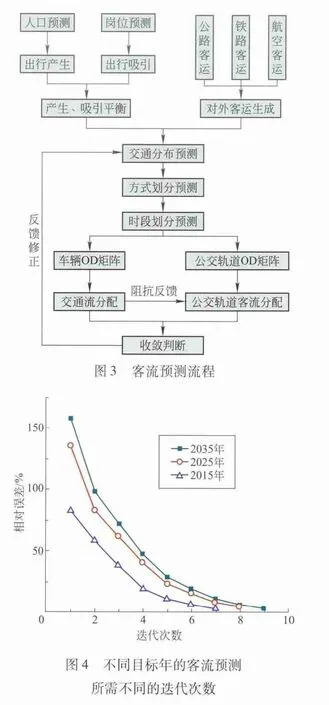
3号线初期、近期和远期日均客运量分别为25.82万、43.03万和66.72万人次，其高峰小时单向最大断面客流量分别为1.19万、1.81万和2.53万人次。表3为轨道交通3号线各特征年客流指标预测值。从图中的客运量可以看出，3号线在开通10年内，客运量年增长7.6%，之后15年，平均年增长3.0%，客流量增长趋势符合增长规律和特征［10］。

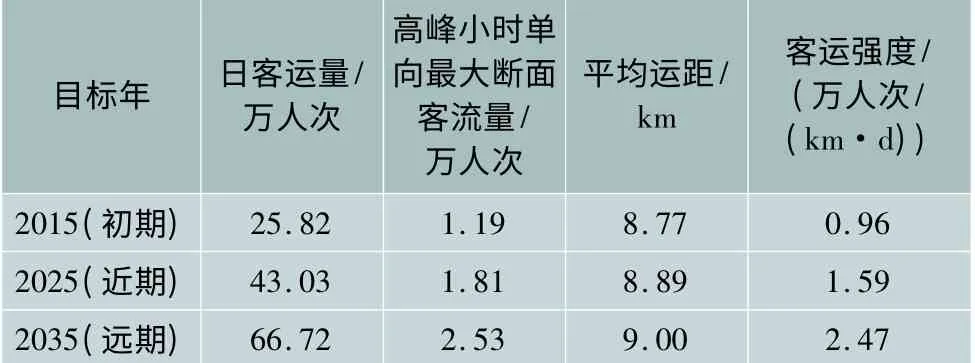
表3 客流指标预测值

4 结论

文中采用扩展反馈四阶段轨道交通客流预测方法对重庆3号线的客流进行预测分析和研究，在数据处理、模型构建和应用及结果分析等方面有一定的进展。对传统的四阶段法进行了改进，扩展了时段划分，加入了反馈修正步骤。通过考虑交通分布、方式划分模型的互相作用，迭代反馈修正模型参数，使得预测结果达到平衡收敛。预测重庆轨道交通3号线的客流，并对结果进行分析，表明增长趋势符合客流变化规律和特征。

［1］过秀成.基于合作竞争类OD联合方式划分轨道客流分配模型研究［J］.中国公路学报，2000(4):57-59.

［2］沈家军，王炜，陈峻.基于灰色马尔可夫模型的近期公交客流量预测［J］.公路交通科技，2007(9):120-123.

［3］陈聪聪.成都市地铁3号线客流预测研究［D］.成都:西南交通大学，2011.

［4］叶霞飞，明瑞利.东京、首尔轨道交通客流成长规律与特征分析［J］.城市交通，2008，6(6):16-20.

［5］潘罗敏.基于时间序列分析的单日地铁短时客流量预测研究［J］.时代经贸，2011，12(10):63-64.

［6］周厚文.浅析城市轨道交通的运营数据管理［J］.世界轨道交通，2011(10):393-396.

［7］杨军，侯忠生.一种基于灰色马尔科夫的大客流实时预测模型［J］.北京交通大学学报:自然科学版，2013(4):119-128.

［8］张晓明.城市交通出行生成模型的研究［D］.北京:北京工业大学，2000.

［9］Ben-Akiva M，Lerman S R.Discrete choice analysis:theory and applications to travel demand［M］.Cambridge:MIT Press，1985:276-285.

［10］陈大伟，肖为周，李旭宏，等.迭代反馈约束下的城市轨道交通客流预测分析术［J］.华南理工大学学报:自然科学版，2011(8):99-102.