线夹回转式导线阻尼间隔棒防舞模型与评估方法
2014-02-13刘连光赵强葛江锋刘自发姚建生仇坚朱小强
刘连光,赵强,葛江锋,刘自发,姚建生,仇坚,朱小强
(1.华北电力大学电气与电子工程学院,北京市102206;2.江苏天南电力器材有限公司,江苏省如皋市226522)
0 引言
输电线路防舞研究是一个世界性的难题,我国是舞动频发的国家,由于各地区的地形、气候条件和输电线路电压等级的不同,防舞的措施和防舞器类型也不同[1],在多分裂导线中,线夹回转式导线阻尼间隔棒由于其特殊的设计结构[2],它的防舞作用受到了广泛关注。其中八分裂线夹回转式导线阻尼间隔棒已在1 000 kV晋东南—南阳—荆门特高压交流试验示范工程17标段中得到应用,对监测结果进行分析之后,其抑制舞动效果达到设计要求,但在特高压电网的建设中能否进一步推广采用该八分裂线夹回转式导线阻尼间隔棒还需进一步研究。目前按同一原理设计的四分裂线夹回转式间隔棒也已在湖北荆门双河和中山口等地的500 kV输电线路中得到应用[3]。
由于国内线夹回转式导线阻尼间隔棒的工程应用时间短,类型较多,装置设计和参数也不统一[4-6],仍缺乏科学、有效的工程试验和理论评价方法。本文提出并建立导线阻尼间隔棒体系的数值模型,并仿真计算导线阻尼间隔棒的防舞效果,以验证该类型间隔棒的舞动抑制作用。
在以往有关舞动的研究中,通常将分裂导线等效为1根单导线,利用单导线的运动方程反映分裂导线的舞动情况,但这种简化不能反映各子导线受空气动力作用的不同情况,也无法处理各子导线不同的约束条件[7]。为了避免复杂的矢量运算,在前人研究工作的基础上[8-9],本文提出基于拉格朗日方程推导的导线三维自由度动力学模型,将罚函数引入到分裂导线阻尼间隔棒与子导线的约束关系中,进而分析并研究导线在间隔棒线夹不同约束条件下的防舞效果。另外,对于一个档距内不同位置装设线夹回转式导线阻尼间隔棒的防舞效果也作了仿真计算,结果表明在1个档距的1/4和3/4处装设该种类型的间隔棒比在档距中点处装设相同的间隔棒的防舞效果更好,这与模态分析的结果相吻合。
1 导线阻尼间隔棒体系的数值模型
1.1 拉格朗日方程导线模型
考虑多分裂导线舞动仿真的难度和计算量,本文分析双分裂导线阻尼间隔棒体系的防舞效果。拉格朗日方程建模假设如下:
(1)只考虑2根子导线具有同一阶模态;
(2)忽略导线纵向惯性力的影响;
(3)只考虑单档的情况;
(4)覆冰沿输电导线均匀分布;
(5)各子导线物理参数和初始形状相同。
拉格朗日方程导线动力学模型描述如下:
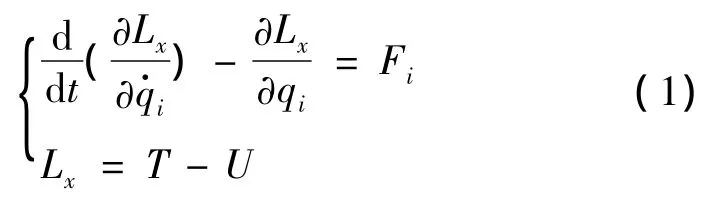
式中:Lx为拉格朗日函数;qi为第i个广义位移;Fi为非保守力对应的广义力;T为系统的总动能;U为系统总应变能。
1.2 导线阻尼间隔棒体系总动能
导线的舞动可分解为横风向(y方向)、顺风向(z方向)和扭转方向的运动。导线截面上任意一点P,动坐标系中坐标为(zP,yP)。当导线扭转角为θ时,P点在固定坐标系中的坐标为

式中Z、Y为导线横截面中心点在固定坐标系中的坐标。
双分裂覆冰导线的动能TL可表示为

将式(2)代入式(3)可得:
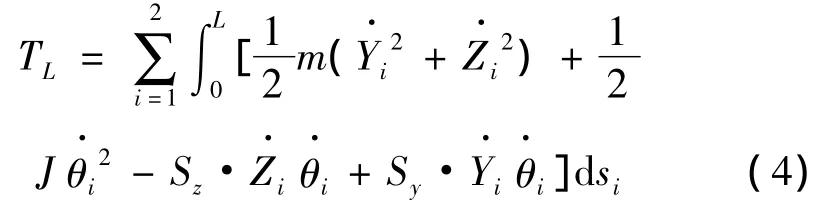
将y、z坐标用横风向广义位移V(t)、顺风向广义位移W(t)及扭转向广义位移Θ(t)替换,可得:

位于Si处的防舞器的动能TF可表示为

式(5)和式(6)相加得导线总动能为

1.3 导线阻尼间隔棒体系总应变能
双分裂导线子导线的初始形状及物理参数一般是相同的,档距L上导线的静态张力T0和初始扭矩M0相等,取相同的值,用EA表示拉伸刚度,用GIP表示扭转刚度。
导线振动为大位移小应变,因此它的应变能为弹性应变能,总应变能可表示为

其中εsi为拉格朗日轴向应变,可表示为

εθi为导线的扭转应变,可表示为
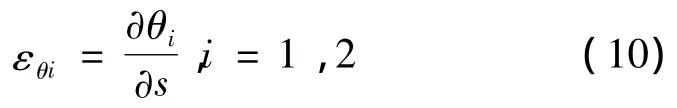
将式(9)、(10)转化为由广义位移表示的应变为

将式(11)代入式(8)可得输电导线阻尼间隔棒体系总应变能U。
1.4 约束条件的引入
约束条件1。2根子导线上由同一根间隔棒所连接的2个点之间的距离保持不变,始终等于间隔棒的长度h。忽略导线轴线运动后,该约束关系可表示为

约束条件2。2根子导线在间隔棒线夹处的转角关系可表示为
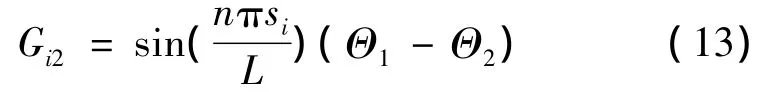
用罚函数法将上述约束条件代入式(1):
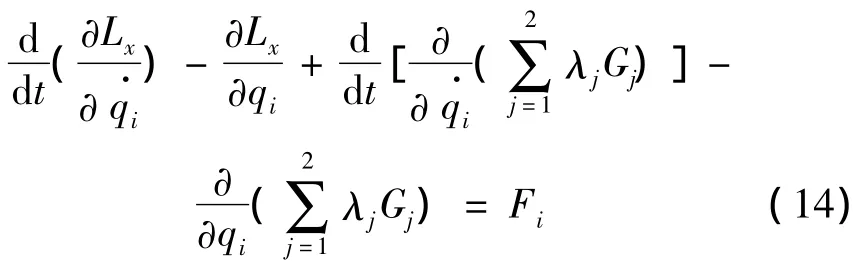
1.5 气动力的确定
导线在某个截面所受的气动力由该截面的风攻角来确定,气动力模型如图1所示。

图1 覆冰导线截面风攻角及受力图Fig.1 Wind attack angle and force diagram of iced conductor cross section
设vz为来流风速,由导线的横风向运动速度及扭转速度导致的风攻角β为
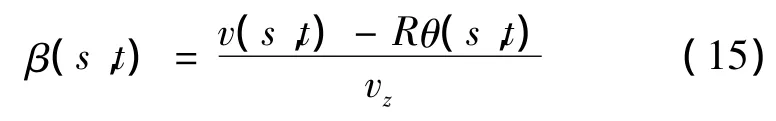
导线在点S处的实际风攻角α为
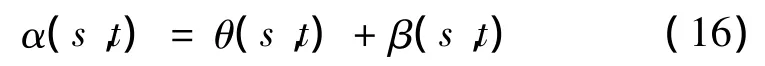
导线截面的气动力F可分解为升力FL、阻力FD、扭矩Fα,计算公式为

式中升力系数CL、阻力系数CD及扭矩系数Cα均为风攻角α的函数。
式(17)为导线截面所受实际气动力,需将其转换到各自由度方向上,由图1可得:
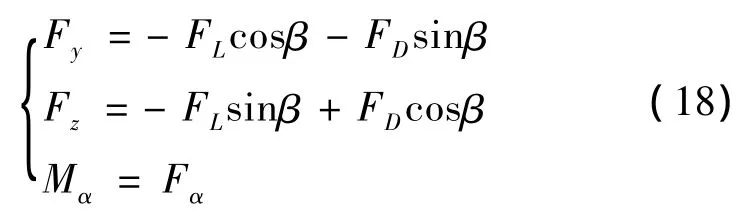
将式(7)、(8)、(18)代入式(14)增广的拉格朗日方程,阻尼按瑞利阻尼表示,可以得到带间隔棒的覆冰分裂导线的运动方程。
1.6 导线数值模型求解
覆冰分裂导线在风载荷作用下的运动方程为非线性微分方程组,本文采用精度较高的四阶龙格-库塔法迭代求解,计算公式如下:

式中:t初始值为0;Δt为给定步长。
根据上述公式的推导,笔者基于MATLAB软件编制了覆冰导线舞动计算程序,利用程序可以模拟不同条件下的导线舞动的响应。
1.7 间隔棒安装位置确定
对固定的一档线路,间隔棒的防舞效果与间隔棒的数量及安装位置密切相关,需要根据线路档距和线路的固有性质(例如材料、形状)计算出间隔棒的最佳安装位置。此外仿真实验得出的数据应该以线路档距中点的横风向的位移为主,这是因为顺风向位移变化较小。
导线舞动主要以1、2、3个半波的振动为主,如图2所示,且导线舞动的波形超过3个半波时舞动的振幅也相应减小,因此在分析导线舞动时以2、3、4个半波的振型分析为主。
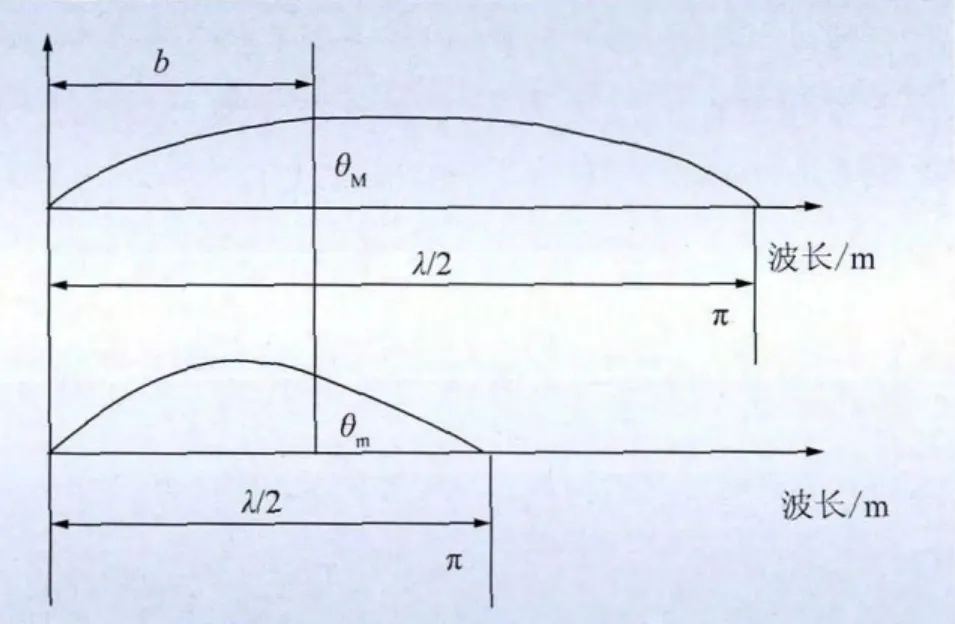
图2 考虑导线最大和最小半波的间隔棒安装位置Fig.2 Installation position of spacers considering the maximum and minimum half-wave of conductor
防舞器安装点对最小半波长及最大半波长这2种情况都应有相同的布置条件(即对波腹的接近程度相同),b为防舞器的安装位置距挂线金具的水平距离,如图2和图3所示,安装位置按照舞动时易出现的2,3,4阶波长综合考虑,可用下面公式确定b:sinθm=sinθM,即有 θm+ θM= π,其中,θM=2πb/λM,表示最大半波长时,间隔棒安装位置离波腹(最大位移处)的接近程度;θm=2πb/λm,表示最小半波长时,间隔棒安装位置离波腹的接近程度;从而可以得到b值即为防舞器的安装位置(F点)[10]。
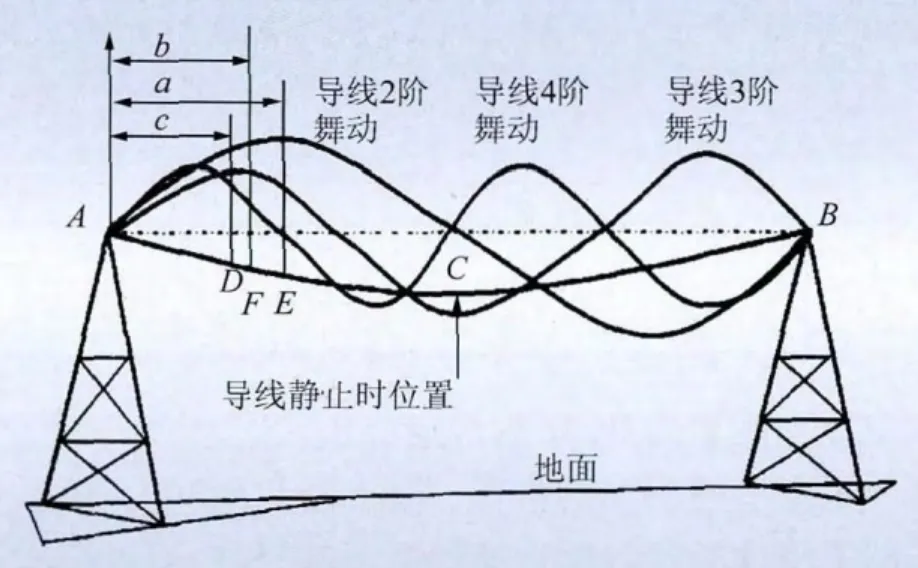
图3 导线舞动波形及防舞器安装位置示意图Fig.3 Conductor galloping waveform and installation position of anti-galloping devices
2 舞动响应数值仿真分析
提出仿真普通间隔棒、不加间隔棒、回转间隔棒和回转间隔棒布置方式等情况的防舞动效果,计算覆冰导线的一阶横风向、顺风向及扭转向的舞动响应,算例引自文献[11],覆冰导线物理参数见表1。

表1 覆冰导线的物理参数Tab.1 Physical parameters of iced conductor
由于缺乏风洞试验数据,计算中假设各子导线上施加的空气动力载荷均相同,即均采用文献[11-13]中的气动力参数,其中,导线风攻角的范围为0°~360°,每隔10°作为一个工况进行仿真计算。3次样条插值法计算得出的升力系数、阻力系数和扭转系数曲线如图4所示。
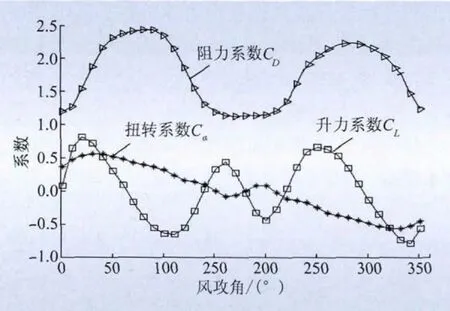
图4 空气动力系数Fig.4 Aerodynamic coefficient
2.1 不同类型间隔棒防舞效果
按表1物理参数和图4中的空气动力系数,沿导线方向间隔50~60 m,分别讨论3种情况:布置3根固定式间隔棒、不加间隔棒和线夹回转式间隔棒的情况,计算子导线1中点横风向、顺方向和扭转舞动响应。其中,加线夹回转导线阻尼间隔棒的子导线1中点的舞动响应如图5所示。

图5 回转式间隔棒的舞动响应Fig.5 Galloping response of rotary spacer
比较这3种情况的结果可知,在初始风攻角为180°、风速为10 m/s、覆冰为10 mm的条件下,不加间隔棒情况的横风向振幅比固定式间隔棒小10%,说明具有降低舞动幅度的作用。在同样的条件下,回转间隔棒最大扭转角达到了20°,而固定间隔棒扭转角最大为10°,横风向的振幅减小为0.9 m,抑制舞动的效果比较明显。说明子导线扭转特性的恢复,使导线的覆冰趋于均匀,即回转式间隔棒能够改善导线的空气动力特性,抑制横风向的舞动振幅。
2.2 间隔棒布置对舞动的影响
按相同的条件,风速取10 m/s,分别在挡距中间位置、1/4与3/4处加装线夹回转式间隔棒,同样可计算子导线1中点横风向、顺方向和扭转舞动响应。其中,1/4与3/4处加线夹回转间隔棒的舞动响应如图6所示。
计算结果表明,在导线1/4和3/4这2处加回转间隔棒比在导线中点处加装间隔棒抑制舞动效果明显,前者横风向舞动振幅为 1.456 m,后者为1.132 m,与模态分析结果吻合。

图6 在1/4与3/4处装间隔棒的舞动响应Fig.6 Galloping responses when spacers are located in the 1/4 and 3/4 of span
3 结论
(1)防舞原理分析和机理验证结果表明[14],可旋转线夹能部分或全部地取消档距内线夹对子导线的扭转约束,从而使得导线覆冰的不均匀程度得到消除或减轻,达到一定的防御舞动的目的。
(2)分裂导线是由间隔棒与多根子导线组成的索梁,系统结构、材料特性和动力学特性极其复杂。使用ANSYS对导线间隔棒体系三维建模及模态分析结果表明,本文采用的Subspace法是求解导线间隔棒体系结构特性、动力学特性的有效方法,广义的Jacobi迭代算法的模态仿真精度高,能反映导线的扭转、变形等情况。
(3)导线间隔棒体系6阶模态的固有频率和振型分析结果表明,本文分裂导线间隔棒体系的6阶振型的仿真分析结果与理论分析结果基本吻合,所采用分析方法可以用于优化导线阻尼间隔棒及其他防舞器的安装位置。了解导线阻尼间隔棒体系对不同类型动力荷载的响应,确定求解控制参数,认识导线阻尼间隔棒体系的固有振动频率和振型,有利于提高防舞效果。
(4)本文采用理论分析和仿真的方法定性地分析了线夹回转式间隔棒的防舞作用。除日本外,回转线夹还有利于恢复、释放子导线的自扭转特性的类似试验,在比利时的恩格、荷兰的普尼姆也都曾做过。其结果都表明线夹回转式间隔棒具有较好的防舞动作用。
[1]陶保震,黄新波,李俊峰,等.1 000 kV交流特高压输电线路舞动区的划分[J].高压电器,2010,46(9):3-7.
[2]牛海军,朱宽军,孙娜,等.1 000 kV间隔棒新型回转线夹设计与应用[J].电力建设,2009,30(2):85-88.
[3]金成生.线夹回转式防舞间隔棒在特高压输电线路中的应用研究[J].上海电力,2010(3):205-209.
[4]朱宽军,刘超群,任西春,等.特高压输电线路防舞动研究[J].高电压技术,2007,33(10):61-65.
[5]赵强,刘连光,姚建生,等.预绞式防振锤的技术特性及其工程应用[J].装备制造技术,2012(4):161-163.
[6]鲍迁.预绞式金具的特点[J].电力建设,2003,24(6):42-43.
[7]李文蕴.覆冰分裂导线舞动数值模拟方法研究[D].重庆:重庆大学,2009.
[8]Desai Y M,Yu P,Shah A H,et al.Perturbation-based finite element analyses of transmission line galloping[J].Journal of Sound and Vibration,1996,191(4):469-489.
[9]孙珍茂.输电线路舞动分析及防舞技术研究[D].杭州:浙江大学,2010.
[10]胡德山.高压导线防舞动模拟及优化方案的研究[D].沈阳:沈阳工业大学,2009.
[11]Yu P,Desai Y M,Shalletal A H.Three-degree-of-freedom model for galloping l formulation[J].Journal of Englneering Mechanies-ASCE,1993,119(12):2404-2425.
[12]Yu P,Desai Y M,PoPPlewelletal N.Three-degree-of-freedom model for galloping 2 solutions[J].Joumal ofEngineering Meehanics-ASCE,1993,119(12):2426-2448.
[13]Desai Y M,Yu P,Popplewell N,et al.Finite-element modeling of transmission line galloping[J].Computers & Structures,1995,57(3):407-420.
[14]刘连光,赵强,刘自发,等.线夹回转式导线阻尼间隔棒防舞机理与模态分析[J].电力建设,2014,35(3):74-78.
