基于粒子群算法的含光伏电站的配电网无功优化

孙卓新，朱永强，倪一峰，叶青，刘颖

(1.新能源电力系统国家重点实验室(华北电力大学)，北京市102206;2.天津国华盘山发电有限责任公司，天津市301900)

0 引言

光伏发电并网系统在一般情况下只提供给电网有功电能，即将太阳能光伏阵列的直流电转换为与电网同频同相的交流电馈送给电网，并保证其具有较高的功率因数。而国家电网公司2011年正式颁布的Q/GDW 617—2011《光伏电站接入电网技术规定》中规定:“对于专线接入公共电网的光伏电站，光伏电站应具备一定无功备用容量，在电网故障或异常时，向电网提供无功支持，防止电压崩溃”［1］。因此需要对含有光伏电站的配电网进行无功补偿。通过合理配置无功补偿装置和有效补偿无功负荷，不仅可以提高节点电压水平，维持系统运行的稳定性，而且还可以降低系统网络损耗，提高电能质量，使配电网络能够安全经济地运行。

所谓无功优化，就是当电力系统的负荷情况及结构参数给定时，通过对控制变量的优化，找到在满足所有指定约束条件的前提下，使系统的一个或多个性能指标(如电压质量最优、有功网损最小、年支出费用最少等)达到最优时的无功调节手段［2］。涉及到无功补偿装置安装地点的选择、变压器分接头的调节配合、无功补偿容量的确定等，是一个多约束的非线性规划问题［3］。目前，无功优化的算法主要分为2类:一是传统的优化算法，如线性规划法、非线性规划法、混合整数规划法、动态规划法等［4-5］，这类算法的缺点是可能无法找到全局最优解;二是人工智能的优化算法，如遗传算法［6］、模拟退火［7］、禁忌搜索［8］、免疫算法［9］等。随机搜索能较好地处理离散、多目标的优化问题是这类算法的一个共同点。粒子群优化算法(particle swarm optimization，PSO)是一种基于群体随机搜索粒子的智能优化算法，最早由Kennedy和Eberhart于1995年提出［10］。该算法源于对鸟群或鱼群捕食行为的研究，是通过对简单社会系统的模拟而发展起来的。虽然简单，却已经显示出很大的应用潜力，目前已应用于电力系统无功电压控制、最优潮流计算以及机组组合等问题。

本文首先分析光伏电站接入低压配电网后影响电压波动的因素，采用并联无功补偿装置在补偿无功的同时改善有功功率，来提高配电网的电压水平。然后以系统运行成本最优为目标函数，包含采取补偿措施后减小的系统网络损耗费用和添加无功补偿装置的费用2个部分，建立含光伏电站配电网的无功补偿优化数学模型。该模型考虑了光伏电站并网逆变器的无功调节能力，并对粒子群算法进行改进，使其具有更好的全局收敛和寻优能力。最后采用多组织粒子群算法对规划模型进行求解，以验证该模型和算法的准确性与有效性。

1 光伏电站对配电网系统电压的影响

电网中各节点的电压水平是由电网的潮流分布决定的，大量光伏电站的接入必然会影响潮流分布，引起各处的电压变化。结合图1所示的光伏电站并网的简单供电线路，来说明线路输送功率与线路电压降的关系。

线路上的电压降满足以下关系:

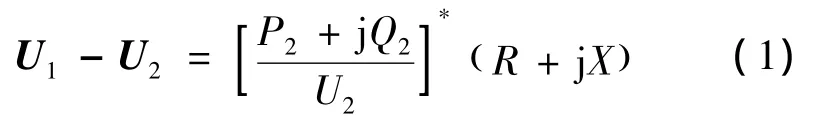
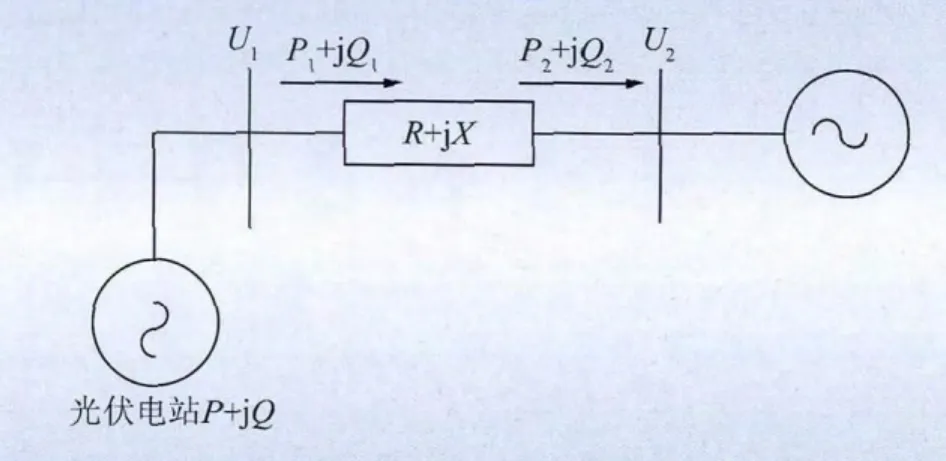
图1 光伏电站并网简单电路Fig.1 Simple circuit of PV power plant parallel in grid

假设线路受端电压的相角为0°，即以 U2=U2∠0°为参考电压向量，则有:

线路两端的电压差为:

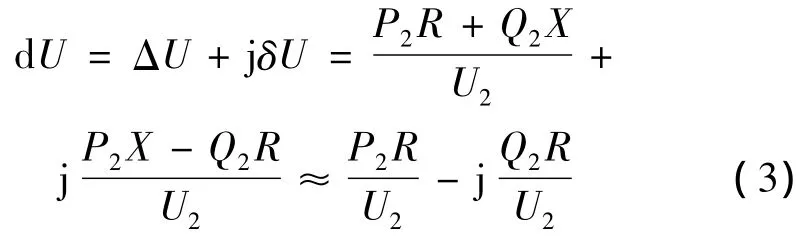
可以看出，光伏电站升压变高压侧电压值与线路输送的有功功率、无功功率及等值线路的R、X值有密切的关系，线路的电阻、电抗一般具有确定的数值，当有功功率沿输电线传递时，线路两端存在电压差。而光伏电站发出的功率是随光照和温度的变化而变动的，那么线路电压降也将是变动的，这将造成节点电压的波动。光伏电站以发出有功为主，只有当需要的时候才发出部分无功功率，因此线路两端电压降的大小将取决于电阻和电抗的取值。

由表1［13］可以看出，对于电压电网线路阻抗主要呈现电阻特性，即R＞X，有时电抗X可以忽略不计。尤其是光伏电站的电气系统，从表2［14］可知目前光伏发电系统发电容量都比较小，一般接入到380 V配电网中，对于含有多个光伏发电系统的光伏电站输出容量可能会大些，一般接入到10 kV或35 kV的电网中。输出线路的截面都不会太大，上述特点更加明显。

由于低压配电网线路的电阻参数大于电抗参数，或者大小相当。如果忽略与电抗相关的项，线路压降表达式为

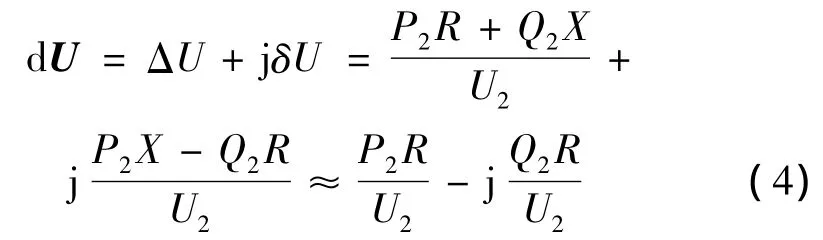
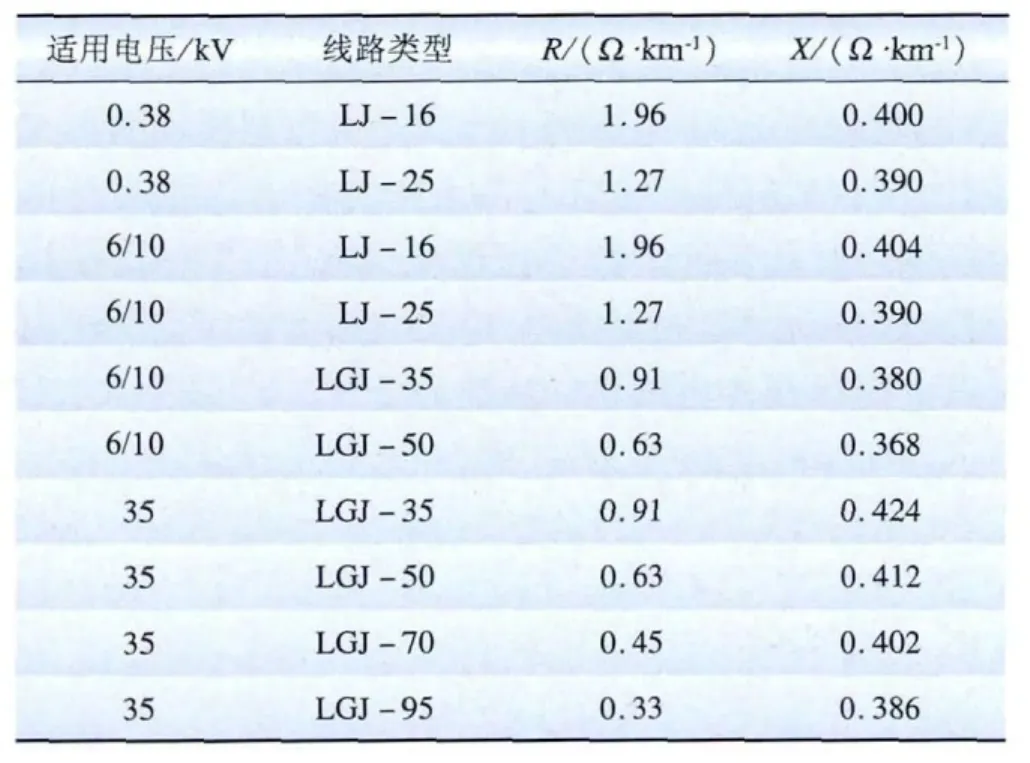
表1 典型输电线路阻抗参数Tab.1 Impedance parameters of typical transmission line

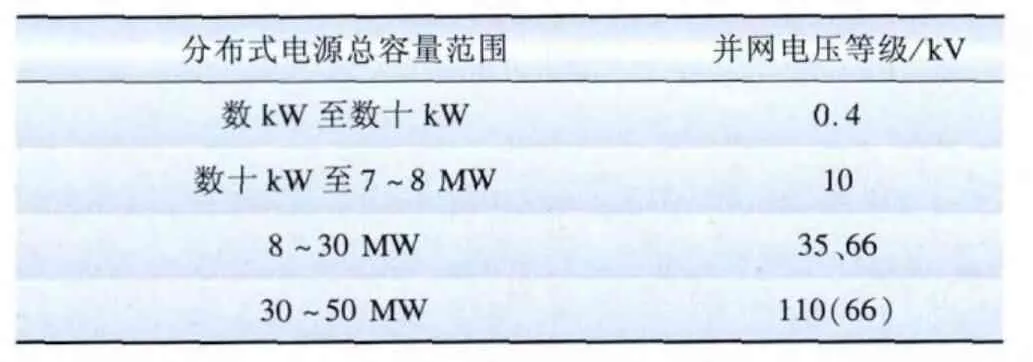
表2 分布式电源并网的电压等级Tab.2 Voltage grade in grid of distributed generation

可见，低压配电网线路的压降横分量ΔU主要受有功的影响，而压降的纵分量δU主要受无功的影响。即低压配电网线路两端电压大小的差别(近似等于ΔU)主要取决于有功功率，而电压的相角差δ主要由无功功率确定。因此当光伏电站有功功率变化时，必然会引起输电线路电压的波动。引起有功功率变化的主要原因是光照和温度的变化，为了追求发电功率的最大化一般不会对有功出力加以限制，因此只能在补偿无功的同时改善有功的影响来抑制输电线路电压的波动。对此本文首先考虑了并网光伏逆变器的无功调节能力，然后采用无功补偿装置进行优化，以改善配电网的电能质量，降低网络损耗，减少系统运行成本。

适用于光伏电站的无功补偿设备目前主要有可投切的并联电容、电抗器、静止无功补偿装置和静止无功发生器等［15］。其中，并联电容、电抗器是无功补偿和电压调节最基本的措施。将电容器、电抗器连接成若干组，根据光伏电站出力水平与网络节点电压变化情况确定每组容量，分组投切，实现无功功率的不连续调节，以保持网络关键节点电压水平处于合理范围。并联电容、电抗器单位容量的投资费用较少，容易安装、方便维护，尤其是并联电容器，运行功率损耗只占额定容量的0.3% ～0.5%，因此目前普遍适用于接入电压等级较低的中小型光伏电站。

2 含光伏电站配电网无功补偿优化模型

2.1 光伏电站的无功调节能力

由于目前广泛使用的光伏逆变器本身具备一定的无功调节能力，因此在进行光伏电站无功补偿优化时应将这部分无功调节能力考虑在内。光伏发电通过逆变器经耦合电感并网［16］，如图2所示。

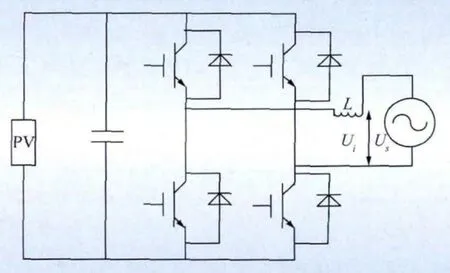
图2 光伏并网逆变器示意图Fig.2 PV grid-connected inverter

系统输出的有功功率为

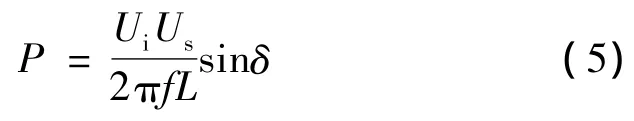
系统输出的无功功率为

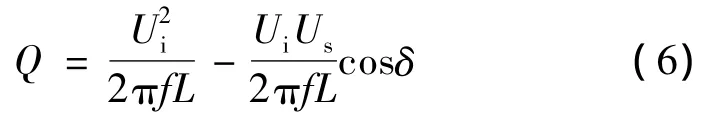
式中:Ui为逆变器输出电压;Us为电网电压;δ为Ui与Us的相角差;L为耦合电感值;f为系统频率。

光伏并网功率调节系统的有功功率输出取决于日照、温度等，系统的无功输出是靠调节Ui与δ来确定的。在光伏并网功率调节系统中，通过改变Ui与δ的大小，来控制逆变器输出电流的有功分量和无功分量，实现对有功、无功的独立调节。当光伏阵列有功率输出时，逆变器将直流电变换成交流电输送到电网上，同时根据相关要求对电网补偿一定的无功电流;当光伏阵列输出的有功功率低于某一限值而停止输出时，逆变器仍然对电网进行一定的无功补偿［17］。

光伏并网系统的无功调节能力是有限的，它取决于并网逆变器的容量和光伏阵列所发的有功功率，其关系式为

式中:Smax表示并网逆变器的容量;表示光伏电站的最大无功调节能力;Pact表示光伏电站所发的有功功率。由于光伏并网系统的无功输出具有连续性和快速性，因此考虑光伏电站的无功输出能力后，不仅节省了无功补偿设备的投资费用，而且改善了配电网系统的电能质量，因此考虑光伏电站的无功输出能力是十分必要的。

2.2 无功补偿优化的数学模型

含光伏电站的配电网在进行无功补偿优化时，其数学模型包括目标函数、功率方程等式约束和不等式约束3个部分。本文选定光伏电站的无功功率调节容量QDG、无功补偿装置的出力QC和有载调压变压器的变比Tt作为控制变量，负荷节点电压值UD作为状态变量。

2.2.1 目标函数

以系统运行最优为目标函数，考虑由于配电网无功补偿而减少的网络损耗费用和添加无功补偿装置的支出费用，其模型表达式为

式中:β为每度电价;τmax为年最大负荷损耗小时数;α、γ分别表示无功补偿设备年度折旧维护率和投资回收率;KC为单位容量无功补偿设备的价格;QC∑为各点无功补偿容量之和;ΔP∑为补偿后的无功网损。

2.2.2 功率方程等式约束

在无功补偿优化模型中，节点有功功率和无功功率平衡约束如下:

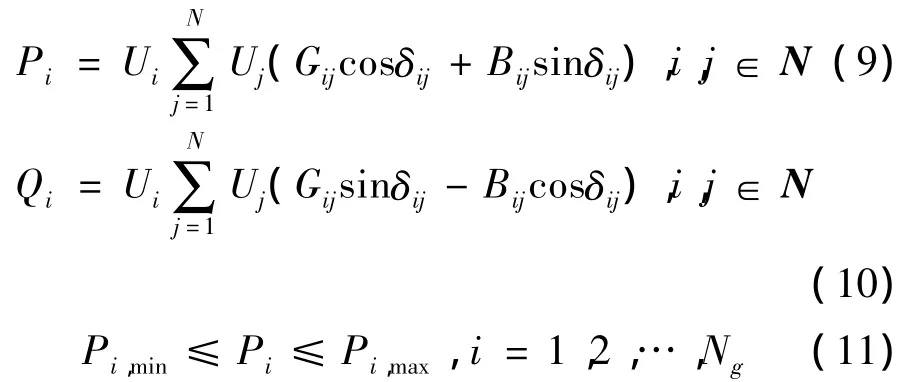
式中N为系统总节点数。

2.2.3 变量约束

变量约束包括控制变量约束和状态变量约束2个部分。本文选定的控制变量为光伏电站的无功调节容量QDG、无功补偿装置的出力QC和有载调压变压器的变比Tt，状态变量是负荷节点电压值UD。

控制变量的约束为:

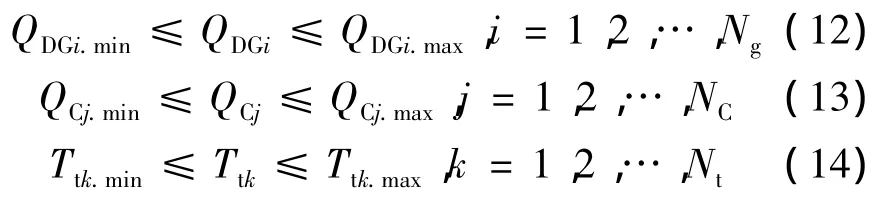
状态变量的约束为

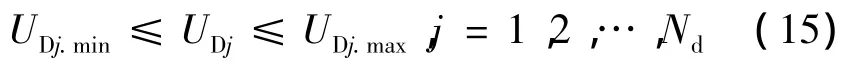
式中:QDGi、QDGi.max、QDGi.min分别为光伏电站的无功容量、无功容量的上限值和下限值;QCj、QCj.max、QCj.min分别为无功补偿容量、无功补偿容量的上限值和下限值;Ttk、Ttk.max、Ttk.min分别为变压器可调分接头及其上限值和下限值;UDj、UDj.min、UDj.max分别为负荷节点的电压、节点电压上限值和下限值;Ng、NC、Nt、Nd分别为光伏电站数、无功补偿装置数、变压器可调分接头数、负荷节点数。

在无功优化问题中，状态变量约束可以采用罚函数法处理。就是将越界的不等式约束以惩罚项的形式附加在原来的目标函数上，从而构成一个新的目标函数。然后对此目标函数进行优化，优化结果可以使控制变量自动满足约束条件，应用此法能够简化优化模型，此时无功优化的目标函数为

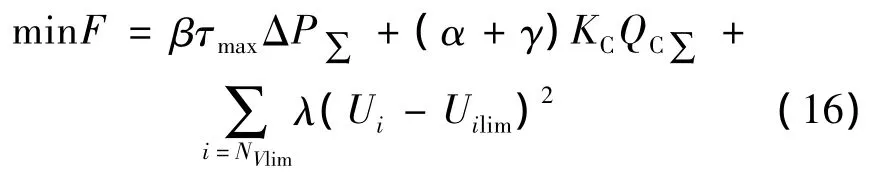
其中:

式中:Uilim为第i节点电压值;Uimax，Uimin分别为节点电压Ui的上限和下限;λ为罚系数;NVlim为电压越限的母线集合。

3 粒子群算法在无功补偿优化中的实现

3.1 多组织粒子群算法

基本粒子群算法由于采用常数惯性权重，寻优结果往往不够理想。此外所有粒子都使用相同的Gbest来更新速度和位置并朝这个最优粒子聚集，容易陷入局部最优解，因此本文提出改进的多组织粒子群算法进行优化求解。首先构造出若干个组别，每个组别中都包含相同数目的粒子。每一个组别都通过与其邻居的竞争或合作进行操作和自学习操作，结合PSO算法的进化机制，不断地通过各组别间的交互作用和每个组别与环境间的相互影响，来更新每组在解空间中的位置，使其能够更快、更精确地收敛到全局最优解。不同于基本PSO算法的是:粒子在每一次迭代中，除了跟踪个体极值Pbest和全局极值Gbest外，还要跟踪组织(Multi-group)中的最佳值 Mbest［18］。在MPSO算法中，粒子i的速度和位置的更新方程为:

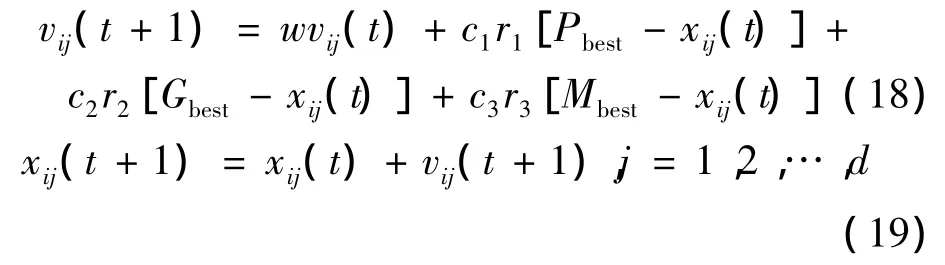
式中:c1，c2，c3为加速系数(或称学习因子)，分别调节向全局最优粒子和个体最优粒子方向飞行的步长，合适的c1，c2，c3可以加快收敛速度且不易陷入局部最优，通常令 c1=c2=c3=2;r1，r2，r3为［0，1］之间任意可能的随机数;Pbest为粒子的个体最优点的位置(即坐标);Gbest为整个种群的全局最优点的位置;Mbest为各组别最优点位置。

3.2 算法的程序设计及流程图

本文利用Matlab中的Matpower工具包进行潮流计算，从而计算出网损。主程序为多组织粒子群算法，生成的随机控制变量送入 Matpower中，在Matpower中计算网损参数，将每个粒子对应的网损返回主程序，用每组控制变量对应的网损加上罚函数就可以得出对应的适应值。再根据粒子群算法的更新原则，更新控制变量。控制变量更新之后，再次送到Matpower中计算网损。其基本思想如图3所示，粒子群算法流程图如图4所示。

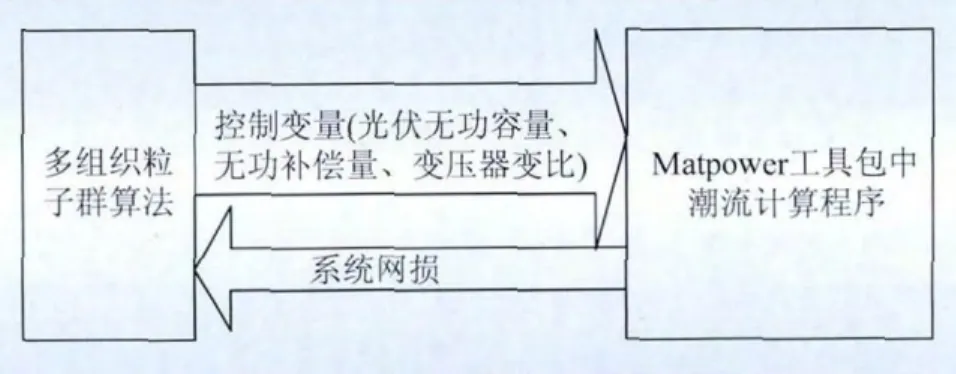
图3 程序设计基本思想Fig.3 Basic idea of program design

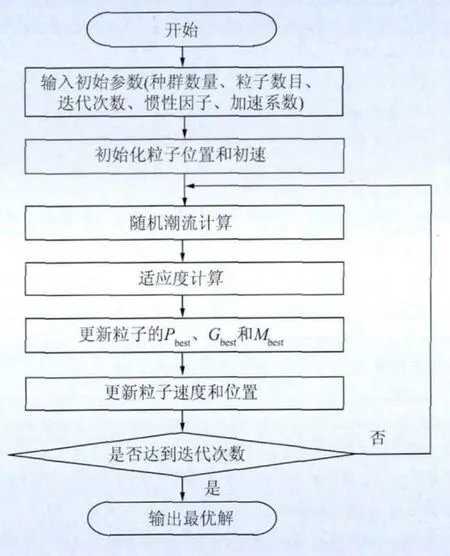
图4 粒子群算法流程图Fig.4 PSO flow chart

4 IEEE 9节点算例分析

运用MATLAB对IEEE 9节点算例进行无功补偿优化计算，来验证MPSO算法的优化效果。首先对IEEE 9节点配电系统网络参数进行修改，如图5所示，参数均以100 MVA为基准值。在节点6加入光伏电站(用PV表示)，光伏电站出力为10 MW。3台变压器，其变比调节范围为［0.9，1.1］，共有9档分接头，调节步长为2.5%。设1个并联电容补偿器。各节点电压的上下限为［0.9，1.1］(标幺值)。节点7装有无功补偿装置，分5档投切，步长为10，其补偿上限为50 Mvar。λ=1 000，为违反电压约束的惩罚因子，节点电压初始值为1.0，初始系统的有功功率损耗为4.955(标幺值)。

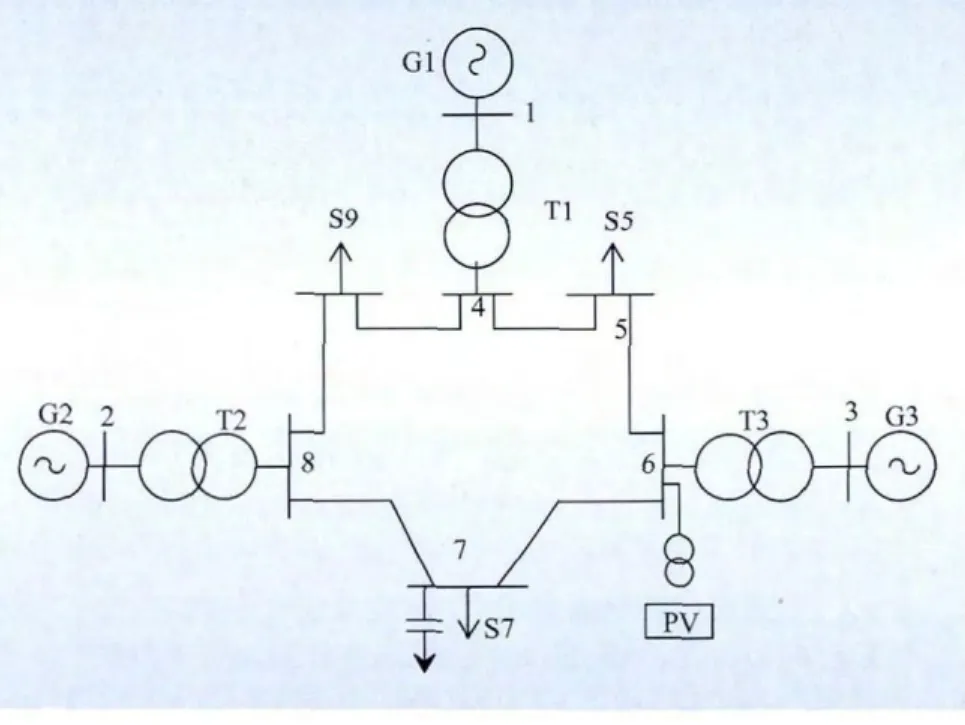
图5 IEEE-9节点系统结构图Fig.5 IEEE9 node system structure

对此配电网系统采用多组织粒子群算法进行优化，并与标准粒子群算法的优化结果进行比较。MPSO算法中的各参数取值分别为w=0.5，c1=2，c2=2，c3=2，种群粒子个数为60，组织数为5，迭代次数为50次。β=0.2元/(kW·h)，τmax=5 000 h、α，γ均取0.1，KC=100元/kvar。优化结果如表3所示。

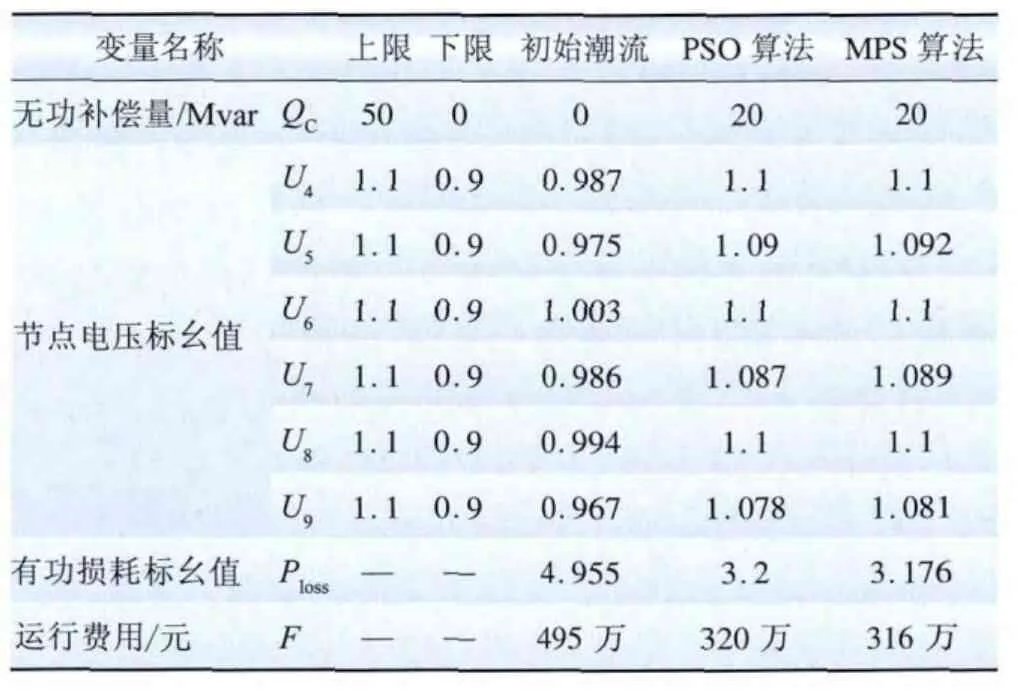
表3 IEEE-9节点系统潮流对比Tab.3 IEEE-9 bus system trend comparison

通过系统运行费用及网损量可以看出，对含光伏电站的配电网进行无功补偿可以降低网络损耗，从而减少费用。MPSO、PSO算法可以获得比较理想的优化结果，MPSO算法具有更强的全局搜索能力，能够有效地摆脱局部最优解。由图6可以看出，在计算速度上，MPSO算法也具有很强的优势，能够以极快的速度获得最优解。通过对无功优化前后节点电压值的比较，可以看到无功优化前，各节点电压值普遍较低，采用MPSO算法进行系统无功优化后，系统整体的电压水平得到了很大的提高，且均在电压限值范围之内。

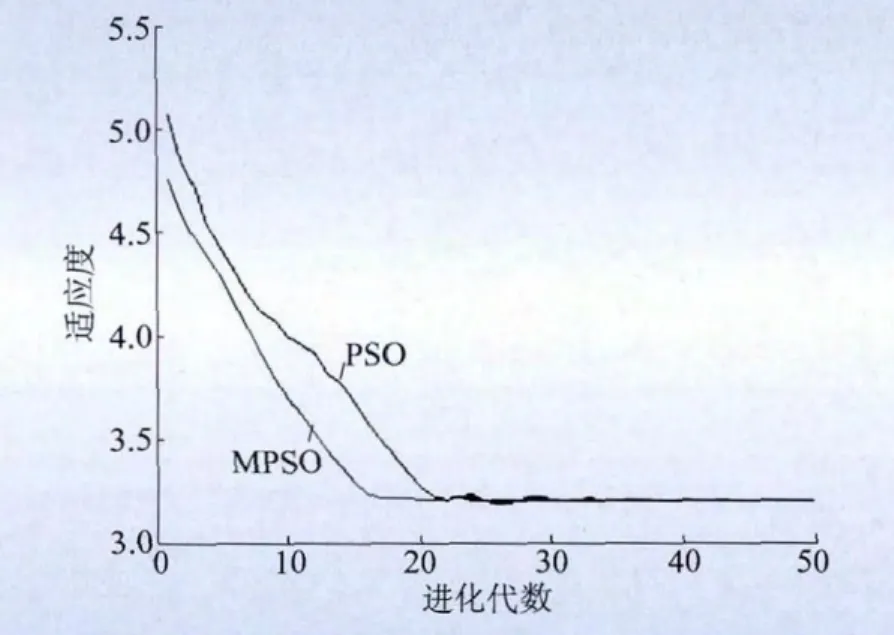
图6 MPSO和PSO适应度进化曲线Fig.6 Fitness evolution curve of PSO and MPSO

如果在进行无功优化时，不考虑光伏电站无功功率的输出，优化结果 IEEE-9节点的网络损耗为3.305(标幺值)，系统运行的费用会高很多。优化结果显示各节点的电压合格率也会有所降低。总体来看将光伏电站的无功功率输出考虑在内，对系统运行的经济性和稳定性都很有利。

5 结论

本文应用现有无功补偿手段并将光伏电站自身的无功调节能力考虑在内，综合各种约束条件，以运行费用(包括系统网络损耗费用和无功补偿装置费用)最低为目标函数，建立了含光伏电站的配电网无功补偿优化模型，并对传统的粒子群算法进行改进，采用多组织粒子群算法进行优化。通过算例计算分析，优化结果表明采用这种方法确定的补偿方案能够有效地减少损耗，提高系统运行的电能质量和经济性，从而证明了模型及算法的快速性和有效性。

［1］Q/GDW 617—2011光伏电站接入电网技术规定［S］.北京:国家电网公司，2011.

［2］郭康，徐玉琴，张丽，等.基于智能单粒子算法的含光伏电站配电网的无功优化［J］.电力科学与工程，2011，27(8):28-32.

［3］许杏桃.地区电网无功电压优化运行与安全控制［J］.电力建设，2004，25(12):36-40.

［4］Deeb N，Shahidehpour S M.Linear reactive power optimization in a large power network using the decomposition approach［J］.IEEE Transactions on Power Systems，1990，5(2):428-438.

［5］Manzoni A.Power systems dynamics simulation usingobjectoriented programming［J］.IEEE Transactions on Power Systems，1999，14(1):39-42.

［6］向铁元，周占山，李富鹏，等.小生境遗传算法在无功优化中的应用研究［J］.中国电机工程学报，2005，25(17):48-51.

［7］顾丹珍，徐瑞德.一种地区电网多目标无功优化的新方法:改进模拟退火算法［J］.电网技术，1998，22(1):71-74.

［8］Wen E S，Chang C S.Tabu search approach to alarm processing in power systems［J］.IEE Proceedings-Generation，Transmission and Distribution，1997，144(1):31-38.

［9］熊虎岗，程浩忠，李宏仲.基于免疫算法的多目标无功优化［J］.中国电机工程学报，2006，26(11):102-108.

［10］张文，刘玉田.自适应粒子群优化算法及其在无功优化中的应用［J］.电网技术，2006，30(8):19-24.

［11］姜惠兰，陈平，王敬朋，等.改进粒子群算法在电网无功优化中的应用［J］.中国电力，2011，44(12):11-15.

［12］陈功贵，李智欢，孙永发，等.电力系统无功优化的LRS－PSO算法［J］.电力系统及其自动化学报，2008，20(4):92-97.

［13］朱永强，迟永宁，李琰，等.风电场无功补偿与电压控制［M］.北京:电子工业出版社，2012.

［14］Q/GDW156—2006城市电力网规划设计导则［S］.北京:国家电网公司，2006.

［15］张程，王主丁，张宗益，等.一种规划态配网无功补偿估算方法［J］.电力建设，2010，11(31):24-29.

［16］Braun M.Reactive power supply by distributed generators［C］//IEEE Power and Energy Society General Meeting，Pittsburgh，USA，2008:1-8.

［17］郭康，徐玉琴，张丽，等.计及光伏电站随机出力的配电网无功优化［J］.电力系统保护与控制，2012，40(10):53-58.

［18］盛慧慧.基于变异特性的多组织粒子群优化算法的无功优化［D］.北京:华北电力大学，2006.