地下工程开挖面空间效应特征研究及应用

乔丽苹，刘 杰，李术才，王者超，姜彦彦，王子豪

（1.山东大学 岩土与结构工程研究中心，济南 250061；2.高唐县人民政府建设工程招投标管理办公室，山东 聊城 252800；3.中国科学院武汉岩土力学研究所，武汉 430071）

1 引言

地下工程开挖过程中开挖面具有空间效应，表现为开挖面对洞周围岩变形的约束作用。由于开挖面的空间约束作用，地下工程开挖后围岩的应力释放不是瞬间完成，而是逐步释放，直到开挖面的空间约束效应完全消失，围岩应力才得以全部释放[1－2]。

针对地下工程开挖面空间效应，国内外学者做了大量研究。孙钧等[1]采用广义虚拟支撑力法模拟开挖面时空效应，开展了隧道二维半黏弹塑性分析。于学馥等[3]建议采用释放系数法模拟隧道开挖时工作面的约束作用。朱维申等[4]利用洞壁径向位移释放系数反映开挖面径向虚拟支撑力的释放。Galli等[5]开展了隧道施工过程三维数值分析，研究了围岩和衬砌在隧道推进过程中的相互作用。金丰年等[6]应用黏弹性力学模型，分析了开挖面与开挖隧道对隧道稳定性影响。王军等[7]对不对称连拱隧道中墙的破坏机制以监控量测为主的数据统计的方式展开研究。王者超等[8]研究了分岔隧道施工过程中存在的空间效应。赵旭峰等[9]计入围岩流变效应、考虑深部软岩隧道时空效应影响，得出在作业面影响范围内开挖面空间效应占主导因素。李煜舲等[10]采用监测数据分析了开挖面掘进效应和约束损失。上述研究为不同工程背景下分析和掌握地下工程开挖面工程效应提供了重要依据。

近些年来，安全风险管理重要性得到人们的接受和认可，目前国家和地方规范和标准是进行地下工程风险识别与评估的基本依据，但目前风险管理相关技术控制规范不够全面，不能满足不同地质条件下地下工程建设需求[11－12]。因此，如何提出相关风险阀值确定方法及建立相应数据库已是当务之急[11]。大型地下洞室断面大、空间效应明显，如何在施工过程中选取稳定性控制标准是一个亟待解决的问题。

本研究中开展地下工程开挖面空间效应现场试验，获得了开挖面空间效应特征，根据试验结果，提出了描述开挖面空间效应经验公式，分析了开挖面空间效应特点；结合地下洞室工程，采用有限单元法，并利用上述经验公式，开展了主洞室围岩稳定性安全控制标准研究。研究结果可为深入了解地下工程空间效应和开展地下工程稳定性控制提供了借鉴和参考。

2 开挖面空间效应现场试验

2.1 工程概况

为了研究地下工程开挖面空间效应，结合某地下洞室工程开展了现场试验。该地下洞室工程是国内首个正在实施的大型地下水封石油洞库建设项目。工程库址区属低山丘陵地貌，地面平均标高220 m，最高点标高为350.9 m。根据地质勘察报告，库址区内的地层主要为晚元古界花岗片麻岩，主要矿物为钾长石、斜长石、石英、角闪石黑云母，细粒花岗片麻结构，块状构造，岩体较破碎～较完整，占洞库岩体80%以上，属坚硬岩。

地下工程主要包括2条施工巷道，9个主洞室和5条水幕巷道，见图1。地下储库由9个主洞室组成。2条施工巷道入口位于洞库南侧，设计标高均为70 m，分别沿洞库东西两侧向北延展，至洞库北端交汇，并沿主洞室方向3个支叉向南延伸至洞库南部，总长度为5 819 m，终端设计标高为 -30m，平均坡降约为13.3%。施工巷道洞跨为9 m，洞高为8 m。9个洞室按南北偏西平行设置。洞室设计底板面标高 -50m，长500～600 m不等，设计洞跨20 m，洞高30 m，截面形状为直墙圆拱形。为了保证洞库密封性，在主洞室拱顶以上25 m处设置5条水幕巷道，水幕巷道轴线垂直于主洞室方向布置设计洞跨为5 m，洞高为4.5 m。按照设计要求，施工过程中水幕巷道先于主洞室开挖完毕。

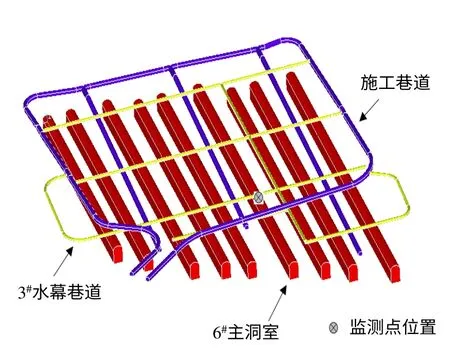
图1 地下结构布置图与监测点位置图Fig.1 Layout of underground structure and position of test

2.2 试验方案

在3#水幕巷道底板向6#主洞室方向钻孔，提前预埋了多点位移计，埋设位置见图1。为了获得不同位置位移变化特征，采用了4测点位移计，测点布置见图2。1#～4#测点分别距离主洞室拱顶12.0、5.0、2.0、0.5 m。测试所用多点位移计由传感器、基座、测杆及锚头组成。位移传感器为振弦式，量程为 200 mm，耐水压为0.5 MPa。钻孔、仪器安装及注浆工作严格按照有关规范执行，确保安装质量。图3为试验现场图片。

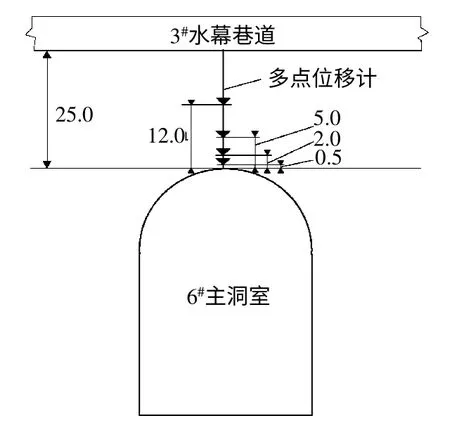
图2 多点位移计埋设图(单位:m)Fig.2 Layout of multi-extensometers used in the field test(unit:m)

图3 现场试验图Fig.3 Procedures of the field test

2.3 试验结果

图4为4个测点沉降值与距开挖面距离关系（图中n为距开挖面距离/隧道洞径）。为便于比较，图中监测断面距开挖面距离进行了无量纲化处理，即横轴为距离与洞宽之比，D为洞跨，在此处取为20 m。分析图中数据可得以下规律：（1）4个测点位移变化规律均表现出显著的空间效应，随着开挖面靠近监测断面，各测点沉降值急剧增大；（2）开挖面远离监测断面时，各测点沉降值趋于稳定；（3）各个测点沉降值与埋设位置有关，距主洞室越近，沉降值越大；（4）在开挖面还未通过监测断面时，各测点均已出现了沉降现象。

3 开挖面空间效应经验公式

为了描述拱顶沉降与距开挖面距离关系，采用双曲正切函数即式（1）拟合现场监测数据。

式中：S为沉降量（mm）；n=L/ D，为无量纲化开挖面与监测点距离，L为监测断面距离开挖面距离，D为隧道洞径；S0、a、c为参数。式（1）满足以下3个条件：（1）n →-∞时，S=0 ；（2）n →+∞时，S=S0；（3）n=c /a时，S=S0/2。其中，S0为隧道最终沉降量。

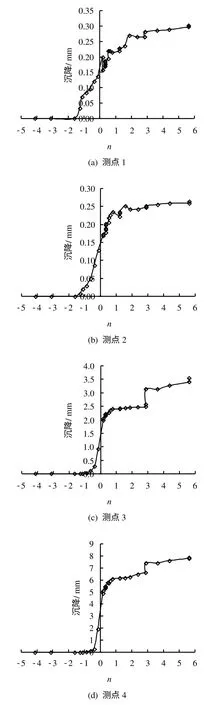
图4 多点位移计各测点沉降与距开挖面距离关系曲线Fig.4 Relation curves of settlement-distance to excavation face and monitoring points

采用式（1）拟合章节2所得监测数据如图5所示。表1为拟合所得参数与拟合相关系数，拟合相关系数均在0.95以上，式（1）较好地反映了现场试验结果。

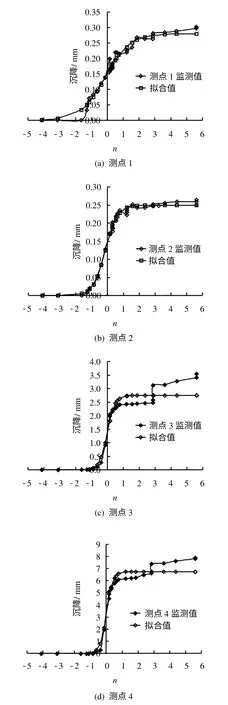
图5 监测拟合沉降与距开挖面距离关系对比Fig.5 Comparison of monitored and fitted settlement-distance to excavation face and monitoring points

分析经验公式特点，式（1）对n 求一次导数可得

从以上的探究中我们可以看出如果将绝对值函数看作是两个函数图像的差距，抽象出这样一个函数模型的话，那么问题三可以分为以下三种图像：（1）当时，如图4，此时函数较为简单，就是平行于x轴的常数函数，此时差距的最大值中，最小值取到时常数函数应该位于。

式中：sec（h(x)）为双曲正割函数。由于一次导数恒大于0，故函数 S (n)为连续递增函数。式（1）对n求二次导数可得

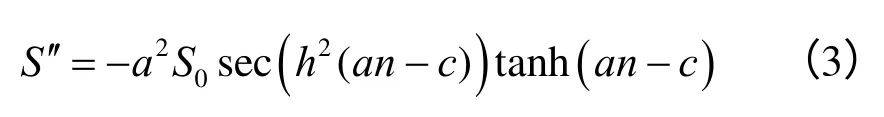
当n=c/ a时，S′=0，n=c/ a为函数 S (n) 的拐点，即开挖面掘进至此处时拱顶沉降位移变化量最大。当n=c /a 时，。因此，开挖面推进至某特定断面时，开挖面对该断面的空间效应并不最为显著。

表1 各测点监测数据拟合参数与相关系数Table 1 Fitting parameters and coefficients of relativity

对监测数据拟合参数分析，测点1～3，c/ a ＞0，空间效应最显著时开挖面已通过该监测断面，而测点4，c/ a＜0，空间效应最显著时开挖面还未通过该监测断面。

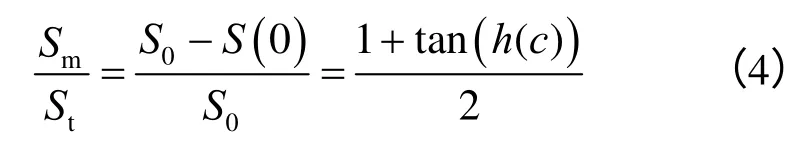
图6为拱顶沉降值与开挖面距离关系全过程曲线。根据上述讨论，图中标注了可监测沉降值、不可监测沉降值与总沉降值之间关系以及沉降变化速率最大处（即二次导数为0的点）。

图6 拱顶沉降-距开挖面距离关系全过程曲线Fig.6 Whole relation between crown settlement and distance to excavation face

表2列出了各个测点监测位移占总位移的百分比。从表中数据可以得到，若开挖后再进行监测，只能监测到总位移的40%～50%。

表2 各测点现场监测位移与总位移比值Table 2 Ratios of monitored settlement over total settlement

目前地下工程开挖与支护设计多采用新奥法。采用该方法施工时，必须开展现场监控量测工作，以获取数据开展围岩参数反分析。限于条件，监测仪器只能在开挖面掘进一段距离后才开始埋设，此时，由于开挖面的部分约束作用已经释放，监测数据不能反映围岩全部变形情况。因此，若直接采用监测数据进行参数反分析，势必会影响所得参数的准确性。

4 开挖面空间效应原理应用

4.1 围岩参数反分析

该洞库水幕巷道施工中采用水准仪开展了拱顶沉降监测，由于水幕巷道施工先于主洞室，因此，本节通过水幕巷道拱顶沉降数据，反演洞库围岩力学参数。表3为水幕巷道典型监测断面拱顶沉降值与其他情况一览表。表中列出了水幕巷道不同围岩条件/稳定状态下监测获得的拱顶沉降值。由表中可以得到，围岩越差，沉降值越大。

采用有限单元法分析水幕巷道掘进过程中开挖面的空间效应。分析中所采用的网格模型如图7所示。模型长80 m，宽80 m，高85 m。

隧道开挖面尺寸为宽5 m，高4.5 m，共剖分单元数4 848个。数值计算中水幕巷道分16步开挖，每步开挖5 m。

表3 水幕巷道典型断面情况Table 3 Information on monitoring sections in water curtain tunnel

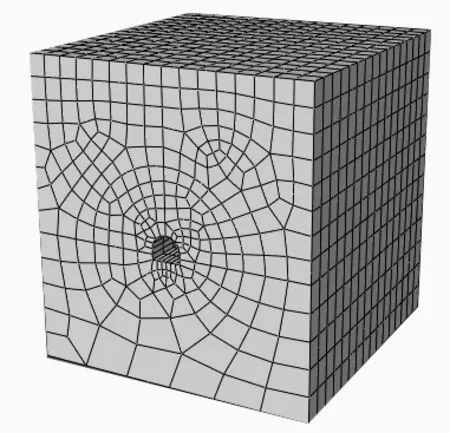
图7 参数反分析所采用有限元网格Fig.7 Finite element meshes used in back analysis of parameters

研究中，假设岩体为弹塑性材料，采用胡克定律描述弹性，采用Drucker-Prager模型描述塑性[13]。岩体弹性模量取为17.1 GPa，泊松比取0.18，密度取2 800 kg/m3。初始应力场根据地应力测试结果施加，最大主应力垂直与巷道轴线，中主应力方向与巷道轴线同向，最小主应力为竖向应力，其值分别为12、8、6 MPa。由于围岩整体较好，支护受力较小，计算中未予考虑支护系统影响。

经反复测试，当围岩力学参数取表4中数据时，模拟预测监测值与监测数据[12]吻合，表中β、d 分别为摩擦角和黏聚力（MPa）。图8为使用表中参数计算得到的沉降-距离关系曲线。采用式（1）拟合计算得到的沉降-距离关系曲线可以获得空间效应特征参数、监测值与总沉降值之比以及预测监测值，结果见表4。从表中数据分析，围岩越差，总沉降量越小，而系数a 和c 逐渐增大。随着围岩变差，可监测值与总沉降值之比逐渐增大，即围岩越差，开挖面空间约束效应越不明显。

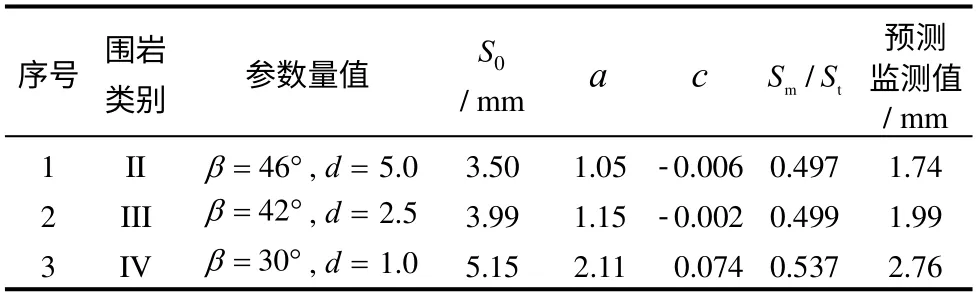
表4 反分析结果Table 4 Results of back analysis

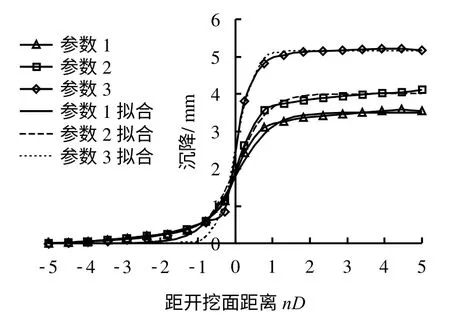
图8 推测与拟合水幕巷道拱顶沉降与距开挖面距离关系曲线Fig.8 Relation curves of predicted and fittingsettlement-distance to excavation face in water curtain tunnel

4.2 主洞室稳定性控制标准

采用章节4.1反分析获得参数，进行了主洞室围岩稳定性分析，获得了不同围岩参数下主洞室拱顶沉降全过程曲线，如图9所示。分析采用与章节4.1相同方法，具体步骤请参考文献[14]。采用式（1）拟合所得曲线，获得了反映主洞室空间效应的参数，见表5。3组围岩参数条件下围岩拱顶的全沉降量量分别为7.06、10.80、12.60 mm，预测所能监测得到的沉降量分别为4.93、6.77、7.60 mm。

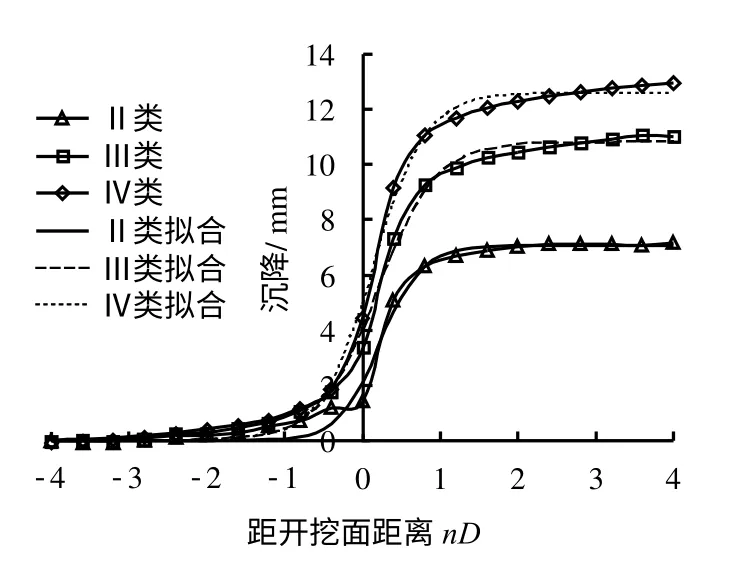
图9 推测与拟合主洞室拱顶沉降-距开挖面距离关系曲线Fig.9 Relation curves of predicted and main cavern fitting settlement-distance to excavation face

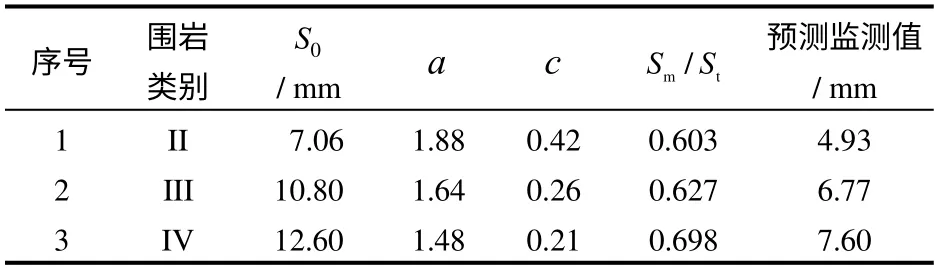
表5 推测主洞室空间效应方程参数Table 5 Predicted parameters of spatial effect

由于计算过程中采用的3组参数分别对应于开挖后围岩稳定、较稳定和较不稳定3种情况，使用这3组参数预测的主洞室位移可以作为主洞室围岩稳定、较稳定和较不稳定3种情况的判断标准。据此，可以得到表6主洞室稳定性预警等级、拱顶沉降控制标准以及建议采取措施。目前该控制标准已在该水封石油洞库中得到应用，取得了较好效果。

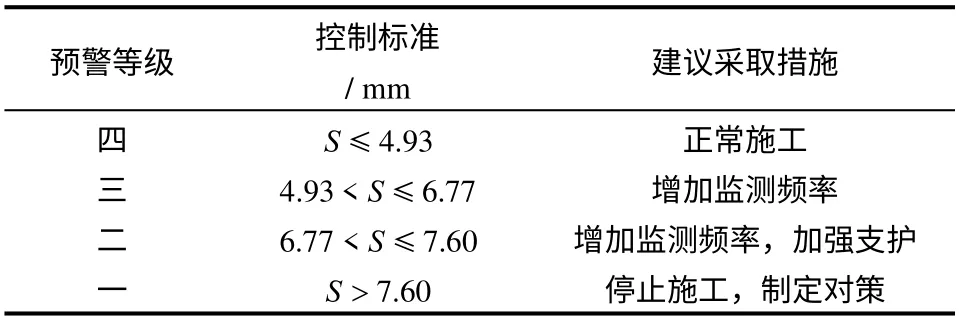
表6 主洞室稳定性控制标准表Table 6 standards of crown settlement for main cavern

5 结论

（1）地下工程开挖面具有显著的空间效应，在开挖面还未通过监测断面时，已发生部分位移。

（2）开挖面空间效应可采用双曲正切函数描述，该函数能较好地反映了开挖面空间效应。对某特定断面，空间效应最显著时并非开挖面透过该断面时。

（3）若采用常规先开挖再监测的方法，不能监测到围岩全部位移，从而影响参数反分析准确性。

（4）随着地下工程围岩变差，开挖面空间约束效应越不明显。

利用上述开挖面空间效应原理，结合水幕巷道监测结果，获得了地下洞室围岩稳定性位移控制标准。

[1]孙钧，朱合华.软弱围岩隧道施工形态的力学模拟与分析[J].岩土力学，1994，15(4):20－33.SUN Jun，ZHU He-hua.Mechanical simulation and analysis of behaviour of soft and weak rocks in the construction of a tunnel opening[J].Rock and Soil Mechanics，1994，15(4):20－33.

[2]杨林德.岩土工程问题的反演理论与工程实践[M].北京:科学出版社，1999.

[3]于学馥，郑颖人，刘怀恒，等.地下工程围岩稳定分析[M].北京:煤炭工业出版社，1983.

[4]朱维申，何满潮.复杂条件下围岩稳定性与岩体动态施工力学[M].北京:科学出版社，1996.

[5]GALLI G，GRIMALDI A，LEONAEDI A.Threedimensional modeling of tunnel excavation and lining[J].Computers and Geotechnics，2004，31(3):171－183.

[6]金丰年，钱七虎.隧洞开挖的三维有限元计算[J].岩石力学与工程学报，1996，15(3):193－200.JIN Feng-nian，QIAN Qi-hu.Simulation of threedimensional tunnel excavations[J].Chinese Journal of Rock Mechanics and Engineering，1996，15(3):193－200.

[7]王军，夏才初，朱合华，等.不对称连拱隧道现场监测与分析研究[J].岩石力学与工程学报，2004，23(2):268－269.WANG Jun，XIA Cai-chu，ZHU He-hua，et al.Site monitoring and analysis of non-symmetrical multi-arch highway tunnel[J].Chinese Journal of Rock Mechanics and Engineering，2004，23(2):268－269.

[8]王者超，李术才，陈卫忠.分岔隧道变形监测与施工对策研究[J].岩土力学，2007，28(4):788－789.WANG Zhe-chao，LI Shu-cai，CHEN Wei-zhong.Deformation monitoring of bifurcation tunnel and countermeasures of construction technologies[J].Rock and Soil Mechanics，2007，28(4):788－789.

[9]赵旭峰，王春苗，孔祥利.深部软岩隧道施工性态时空效应分析[J].岩石力学与工程学报，2007，26(2):406－408.ZHAO Xu-feng，WANG Chun-miao，KONG Xiang-li.Analysis of time-space effects of construction behaviour of deep soft rock tunnel[J].Chinese Journal of Rock Mechanics and Engineering，2007，26(2):406－408.

[10]李煜舲，许文贵，林铭益.以隧道变形量测资料分析掘进效应与约束损失[J].岩石力学与工程学报，2009，28(1):39－46.LEE Yu-lin，XU Wen-gui，LIN Ming-yi.Analysis of advancing effect and confinement loss by using deformation measurements in tunnel[J].Chinese Journal of Rock Mechanics and Engineering，2009，28(1):39－46.

[11]钱七虎，戎晓力.中国地下工程安全风险管理的现状、问题及相关建议[J].岩石力学与工程学报，2008，27(4):649－655.QIAN Qi-hu，RONG Xiao-li.State，issues and relevant recommendations for security risk management of China’s underground engineering[J].Chinese Journal of Rock Mechanics and Engineering，2008，27(4):649－655.

[12]黄宏伟.隧道及地下工程建设中的风险管理研究进展[J].地下空间与工程学报，2006，2(1):14－20.HUANG Hong-wei.State of the art of the research on risk management in construction of tunnel and underground works[J].Chinese Journal of Underground Space and Engineering，2006，2(1):14－20.

[13]中交第一公路工程局有限公司.JTG F60－2009公路隧道施工技术规范[S].北京:人民交通出版社，2009.

[14]姜彦彦.地下水封石油洞库风险分析与评价研究[硕士论文D].济南:山东大学，2013.