走滑断层位错作用下城市地铁隧道损伤分析

赵 颖，郭恩栋，刘 智，高 霖

（1.中国地震局工程力学研究所 地震工程与工程振动重点实验室，哈尔滨 150080；2.东北林业大学 土木工程学院，哈尔滨 150040）

1 引言

地铁隧道是生命线工程的重要组成部分，其抗震问题已经成为城市工程抗震和防灾减灾研究的重点[1]。由于地铁工程线路走向取决于交通功能的要求，导致越来越多的地铁区间隧道不可避免的穿越地震断层。断层错动会对埋地管线、地铁隧道等地下工程产生灾难性的、不可恢复的破坏，甚至会导致结构的整体坍塌。1906年美国西部加州太平洋沿岸的大城市旧金山8.3级地震，穿越圣安德烈斯断层的2座南太平洋铁路隧道遭受严重破坏。1971年美国圣佛南都6.4级地震，5座隧道出现不同程度的震害，其中邻近SantaSuzana和Sylmar断层处的隧道破坏最为严重，最大垂直位错量达2.29 m，混凝土衬砌出现裂缝、脱落等严重现象，而距离断层较远处的3座隧道破坏程度较轻。2008年汶川8.0级地震，处于F3和F2断层之间的龙溪隧道因断层错动形成了约1 m左右的竖向错动变形，导致衬砌拱部塌落。因此，针对跨越地震活断层的地铁区间隧道等地下结构的工程抗震问题的深入研究意义重大。

目前国内外学者对于跨断层隧道的抗震研究已取得了一些有意义的成果。Kontogianni等[2]通过现场试验，研究了隧道衬砌管片环向接头部位在逆断层和走滑断层作用下的应力-应变关系，并总结出不同断层倾角下管片环向接头部位应力-应变的变化规律。Anastasopoulos等[3]利用所建立的非线性有限元计算模型，研究了正断层错动下以及地震荷载作用下深埋隧道的变形，认为在断层倾角为45°～60°的正断层作用下垂直位错量与土层厚度的比值不超过1%，地表就不会产生位错。左娟花等[4]通过砂箱模型试验，研究了断层错动下隧道距基岩面不同距离时位于上覆土体中隧道应变的变化规律。张维庆[5]采用数值模拟计算方法，研究了穿越断层隧道在断层错动和地震惯性力分别作用下的震害机制，研究表明断层错动对隧道衬砌结构的影响较地震惯性力要大。

以上的研究成果，由于面临着一些复杂的问题，如断层破裂机制较复杂、试验结果离散性较大、数值模拟中的局限性等，只得出一些定性的结论，难以用于指导工程实践和抗震设计工作。本文在前人研究成果基础上，以北京地铁7号线区间隧道为背景，采用拟静力有限元计算方法，研究了地铁隧道在走滑断层作用下的非线性反应，通过大量计算建立了能够较快速、较准确地估计出穿越活断层城市地铁隧道的抗震薄弱部位的关系式，以期能为跨断层地铁隧道的抗震设计提供参考。

2 损伤塑性本构模型

沈新普等[6]以大型有限元软件ABAQUS为平台，采用应变协调假设和强度等效假设，提出了钢筋混凝土等效材料的损伤塑性本构模型，模型中的钢筋不再单独定义，而是被等效到钢筋混凝土模型中，通过定义拉伸强化塑性应力-应变曲线实现钢筋的强化特性。沈新普等[6]提出的模型主要对ABAQUS软件中给出的损伤塑性模型的拉伸强化-软化阶段的特性进行了完善，该模型建立的主要思路如下：

根据应变协调假设，即假定钢筋与混凝土粘结完好，两者的应变（εs为钢筋应变，εc为混凝土应变）相等

钢筋和混凝土等效材料的名义应力为

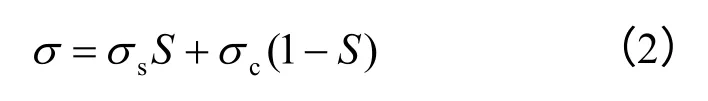
式中：S为钢筋所占的面积比率；σs、σc分别为钢筋、混凝土应力。

由此可得弹性阶段钢筋混凝土等效材料的弹性模量E：

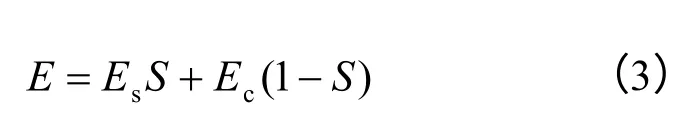
式中：Es为钢筋的弹性模量；Ec为混凝土的弹性模量。

当钢筋混凝土结构受到拉伸荷载时，混凝土首先达到抗拉强度，根据强度等效假设，即假定等效材料的强度与各种组成材料的强度在宏观外在表现相同，可得钢筋混凝土等效材料初始屈服强度σy1：

式中：fct为混凝土抗拉强度。

当钢筋混凝土等效材料的应力超过σy1后，结构所受的荷载主要由钢筋承担，直到钢筋达到屈服荷载fs，此时，钢筋混凝土等效材料的最大屈服极限σy2为

图1为钢筋混凝土等效材料的拉伸应力-应变曲线。假定界面黏结完好，与σy1和σy2对应的应变值可分别按着上述混凝土和钢筋的初始屈服极限及等效材料的弹性模量近似计算，分别为

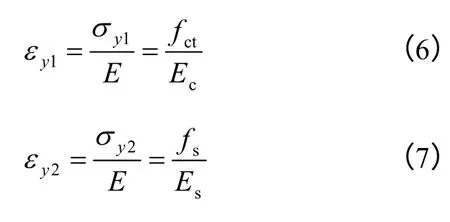
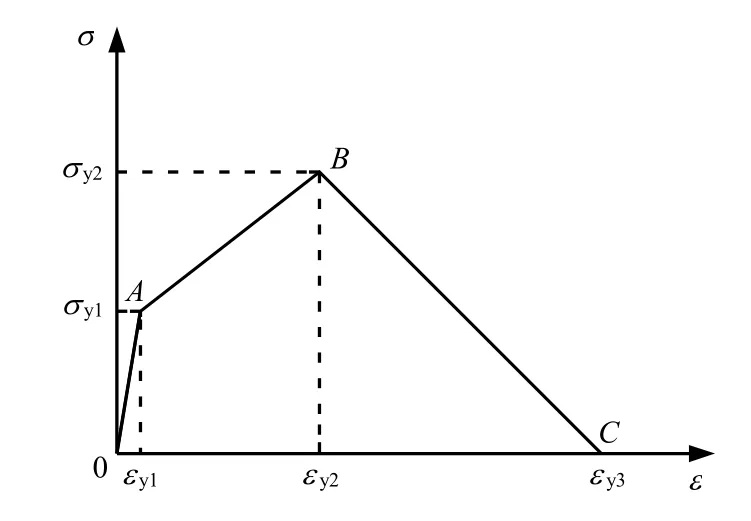
图1 等效材料的拉伸应力-应变曲线Fig.1 Tensile stress-strain curve of the equivalent material

ABAQUS软件中规定，损伤模型以数据系列的形式输入[7]，在拉伸应力状态下采用分段线性损伤演化模型，拉伸应变值与损伤值的对应关系见表1。

表1 拉伸应变值与损伤值的对应关系Table 1 Corresponding relation between tensile strain and damage

由于钢筋混凝土的受压特性主要取决于素混凝土，钢筋的影响很小，可直接采用ABAQUS中提供的具有硬化和软化阶段的压缩损伤塑性模型，如图2所示。本模型为连续的、基于塑性的混凝土损伤模型，屈服或破坏面的演化由压缩等效塑性应变控制，材料达到初始屈服应力值 σc0之前为线弹性，屈服后是硬化段，超过极限应力σcu后为应变软化，此种表示方法抓住了混凝土的主要变形特征[8]。弹性刚度的损伤通过损伤变量dc表示，ABAQUS中损伤变量的定义与演化律是通过其对应的非弹性应变的数值序列给出的[7]，损伤因子的取值范围从0（材料无损伤）～1（材料完全损伤）。

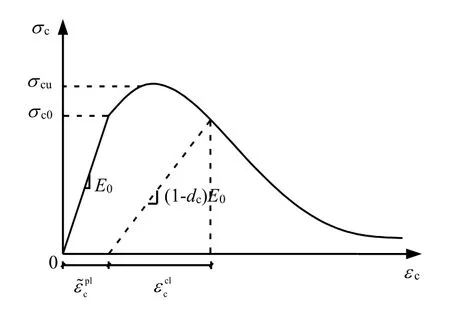
图2 压缩损伤塑性模型Fig.2 Compression damage plasticity model

3 跨断层地铁隧道数值计算模型

3.1 整体模型的建立

以北京地铁7号线工程广渠门内站-广渠门外站区间隧道为分析研究对象，为了建立合理的、符合实际工程情况的计算模型，同时考虑计算效率，计算过程中逐渐增大模型的长度，经多次试算，在断层附近一定范围内衬砌不再发生变化或者变化很小，该长度即确定为合理长度，本计算模型的合理长度取为400 m。模型的横断面尺寸根据目前的经验做法认为取地下结构宽度的5～10倍作为计算区域，超过5倍之后人工边界对于计算结果影响甚微[9]。本工程中隧道衬砌的外径6 000 mm，因此，本计算模型的宽度取60 m。

整体模型结构长400 m，宽60 m，高64 m，上覆土层厚60 m，下部基岩厚4 m，隧道顶板覆土厚14 m，断层破碎带为一倾斜的薄弱岩体，断层破碎带宽50 m。衬砌为圆形单层钢筋混凝土管片结构，内径为5 400 mm，外径为6 000 mm，管片厚300 mm。基岩、断层破碎带、上覆土层采用ABAQUS中的实体单元C3D20R，隧道衬砌采用壳单元S4R来模拟。土层（粉质黏土）、基岩（石灰岩）和断层（砂土）计算参数见表2。隧道衬砌为钢筋混凝土结构，混凝土强度等级为C50，本模型将衬砌结构其等效为连续均质模型，考虑到隧道衬砌各类接头对其刚度的减弱，按照日本隧道规范建议将其弹性模量E 折减20%[10]，其材料性能指标见表3。隧道衬砌结构的拉伸、压缩损伤塑性模型分别选取图1、2的应力-应变关系曲线。考虑到盾构施工特点，假定管片拼装完成后，衬砌与土体始终保持接触状态且不会发生滑移，因此，衬砌与土体之间的接触面采用绑定约束。地基土-隧道体系整体有限元模型见图3。模型X 轴方向为与隧道轴线垂直方向，Y 轴方向为竖直方向，Z 轴方向为隧道轴线的水平方向。

3.2 加载方式及边界条件的设置

基于拟静力弹塑性有限元方法计算断层错动而引发的隧道衬砌结构非线性反应。该方法假定断层错动只是沿一个方向进行，不考虑往复错动和错动速率等因素的影响，采用分步加载增量法，将断层错动分为多次较小的位错，逐步作用在基岩上，从而得到隧道衬砌结构的损伤破坏发展过程。本模型通过给活动盘的左端和底部断面同时施加X 轴负方向的强制水平位移来模拟走滑断层的错动效果。

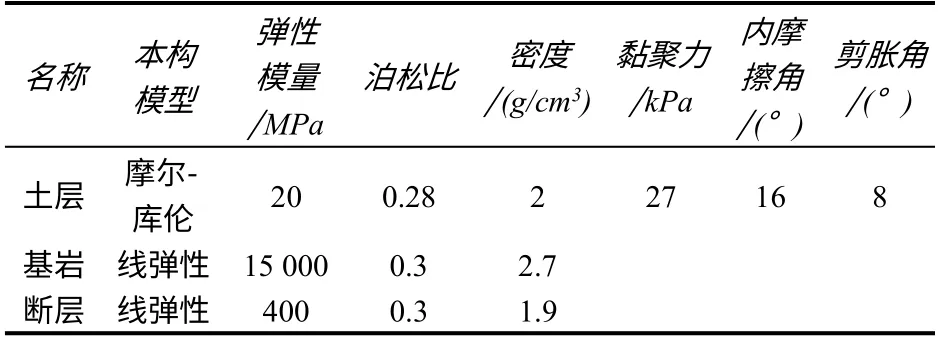
表2 土层、基岩和断层计算参数Table 2 Calculation parameters of soil，rock and fault

表3 混凝土材料性能指标Table 3 Performance index of concrete material

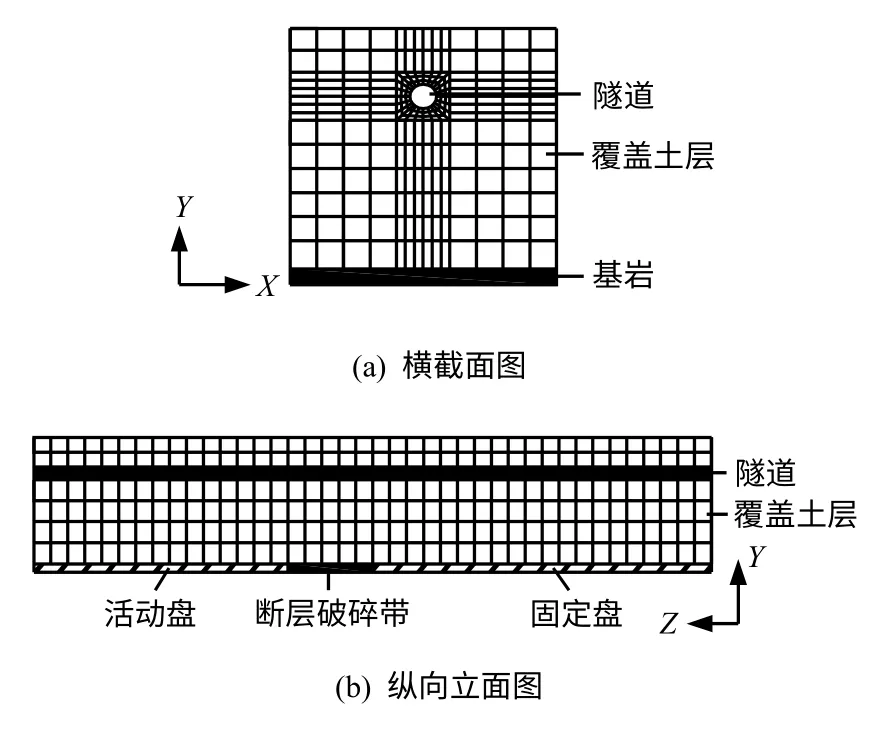
图3 地基土-隧道体系整体有限元模型Fig.3 Soil-tunnel finite element of whole model

位移边界条件：固定盘的底部和右端断面，以及位于固定盘上方的土层的端部施加固定边界；活动盘的底部和左端断面、断层破碎带的底部以及位于活动盘上方的土层的端部约束Y 轴和Z 轴方向的位移，X 轴方向的位移自由。

3.3 模型初步验证

为了对所建立的有限元模型进行初步验证，利用ABAQUS计算了走滑断层下地表产生的位错量D地表，与基于历史震害数据以及采用拟静力弹塑性有限元方法编制的覆盖土层场地地震地表断裂软件计算结果所建立的地表位错计算公式[11]，见式（8），对比结果见表4。采用ABAQUS计算的地表位错略大于统计公式的计算结果，误差均在12%以内，说明利用本文所建立的有限元模型可较准确地模拟走滑断层的错动效果。

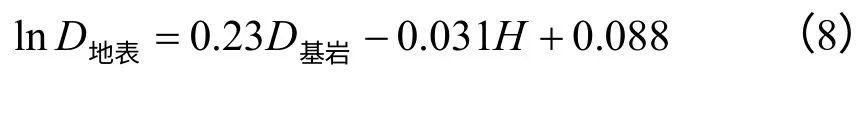
表4 走滑断层下覆盖土层场地地表位错计算结果对比Table 4 Comparision of the result of soil surface dislocation under strike-slip fault

4 计算结果分析

根据世界范围内走滑断层引发的里氏震级为7级以上且伴有地表断裂的典型历史震害数据，回归拟合了基岩位错D基岩与震级M 之间的关系式[11]：

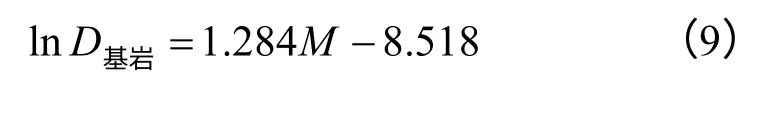
根据式（9）可估算出走滑断层下某一震级M所对应的基岩位错D基岩，当M=7.0时，D基岩≈1.5 m；当M=7.5时，D基岩≈3 m；当M=8.0时，D基岩≈6 m。收集的历史震害资料[11]可以发现，走滑断层引发的地震多数集中在7.0～8.0级之间。

在隧道衬砌结构的拉伸损伤塑性本构模型中，结构在达到最大屈服极限时，定义结构的损伤值Dt=0.1。当损伤值Dt＜0.1时，结构处于安全状态；当损伤值Dt≥0.1时，结构开始出现损伤破坏，且损伤值越大，结构的破坏程度越严重。在隧道衬砌结构的压缩损伤塑性本构模型中，结构在达到初始屈服应力前，定义结构的损伤值Dc=0时，结构处于安全状态；当结构的损伤值Dc＞0时，结构开始出现损伤破坏，且损伤值越大，结构的破坏程度越严重。

4.1 衬砌破坏形式判断

走滑断层主要是由来自两旁的剪切力作用形成的，其两旁顺断层面走向相对移动，而无上下垂直移动。在一次强破坏性地震中，断层区地面发生相对较大的错动，埋于土中的隧道将会随着土体的变形而变形，并受到来自沿隧道轴向和横向的土体反作用力，此时的衬砌受力十分复杂，会受到剪、弯和拉压等作用，并产生拉伸或压缩破坏。

图4为不同土层厚度H 下Dc与Dt的比较曲线。从图中可以看出，当土层厚度H 分别为30、40、50、60、70 m时，随着震级M 的增大，衬砌结构的受压损伤值Dc逐渐增加，而受拉损伤值Dt均小于0.1，可见在走滑断层位错作用下衬砌结构破坏的主要方式是受压破坏，故在以下的分析中主要关注隧道结构受压损伤的非线性行为。

4.2 结构损伤分析

图5为M=8.0、H=40 m时走滑断层下衬砌结构损伤曲线。从图中可以看出，走滑断层作用下隧道结构的拱腰部位的损伤最为严重，其次为拱底，拱顶处的损伤相对较轻。结构出现损伤的区域主要发生在断层破碎带上方及其附近一定范围内，离断层较远处结构完好，与震害调查中所得到的“隧道在断层错动下的损伤破坏只发生在活断层附近的一定范围内”相符合，再一次验证了本文所建立的有限元模型的合理性。由于场地土均匀，走滑断层作用下隧道结构拱腰部位的损伤分布呈反对称形式。

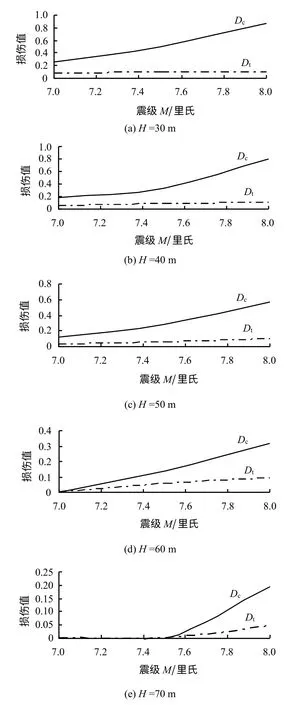
图4 不同土层厚度H 下Dc与Dt的比较曲线Fig.4 The comparison curves of Dcand Dtunder different soil thicknesses

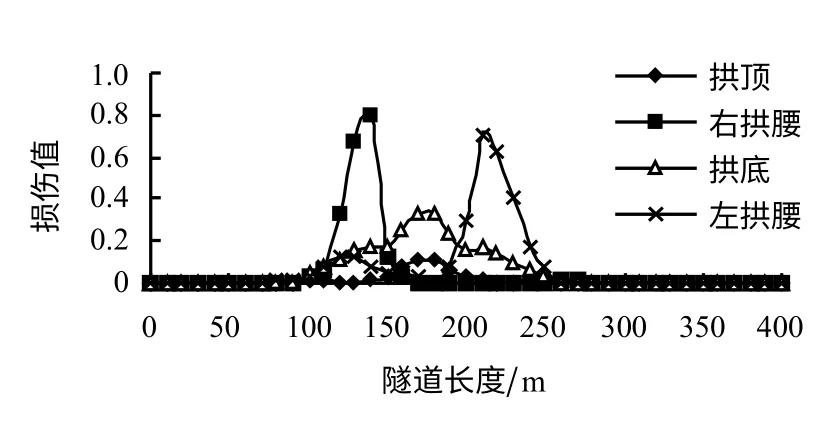
图5 M=8.0，H=40 m时走滑断层下衬砌结构损伤曲线Fig.5 The damage curves of lining structure under strike-slip fault when M=8.0，H=40 m

图6为隧道结构损伤平面图。隧道结构的损伤区域主要位于断层线的两侧，损伤区间是指（-a，b），损伤区域长度L损伤=a+b。

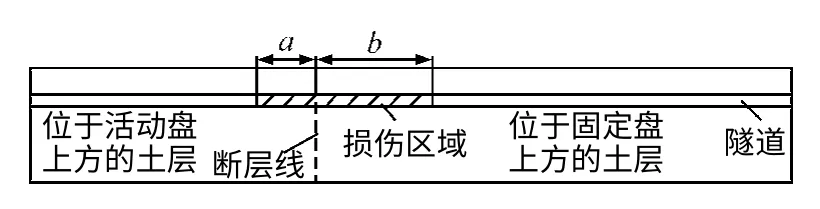
图6 隧道结构损伤平面图Fig.6 Damage plan of tunnel structure

表5为不同震级、不同土层厚度时走滑断层作用下衬砌结构的最大损伤值。由表中可见，相同基岩上覆土层厚度下震级越大（也就意味着断层错动量越大），衬砌结构的损伤程度越严重；相同震级下随着基岩上覆土层厚度的增加，衬砌结构的最大损伤值逐级减小，当结构的损伤值趋近于0时所对应的土层厚度定义为临界覆盖土层厚度。分析表5发现，可不考虑断层位错影响的临界覆盖土层厚度H临界值与震级M 之间呈线性增长的关系，拟合为如下关系式：

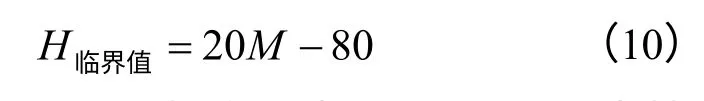
其相关系数R2=1.000，拟合曲线如图7所示。当基岩上覆土层厚度H≥H临界值时，可以不考虑走滑断层断裂对于浅埋隧道的影响，说明基岩上覆土层厚度增加时能够减轻隧道结构的破坏程度，因为具有一定厚度的上覆土体对基岩错动量具有一定的吸收作用，土层厚度足够大时断层错动不会造成隧道结构的破坏。

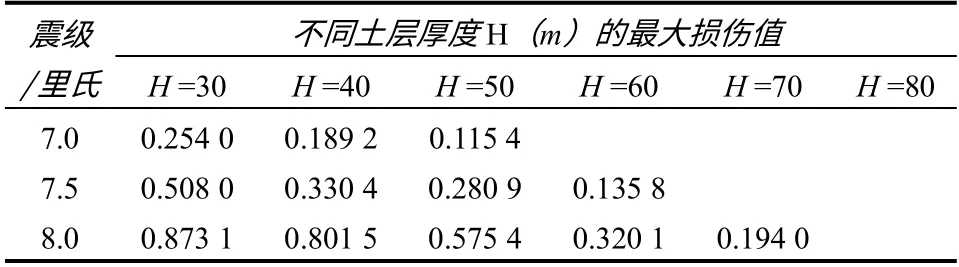
表5 不同震级、不同土层厚度时衬砌结构的最大损伤值Table 5 Maximum damage of lining structure under different magnitudes and soil thicknesses

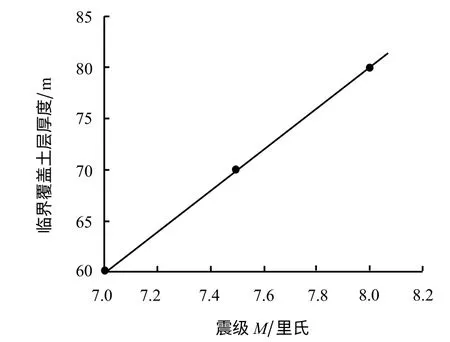
图7 临界覆盖土层厚度与震级关系拟合曲线Fig.7 Fitting curve of relation between magnitude and critical value of soil thickness

表6为走滑断层作用下衬砌结构损伤情况。从表可见，土层厚度一定时随着震级M 的增大（即位错量增加），结构出现的损伤区域长度逐渐增大，土体随断层错动量的增加而逐渐屈服，埋于土中的隧道将会随着土体一起变形，衬砌结构的损伤区沿轴向逐渐延伸扩展；震级M 一定时随着土层厚度的增加，结构发生损伤的区域长度逐渐增加，但损伤值逐渐减小，这是因为基岩上覆土层越厚，结构出现损伤破坏所需要的位错量越大，随着位错量的增加，结构出现的损伤区域范围会逐渐扩大。

对表6中的数据进行多元回归分析，拟合为如下关系式：

损伤区间：（-a，b）

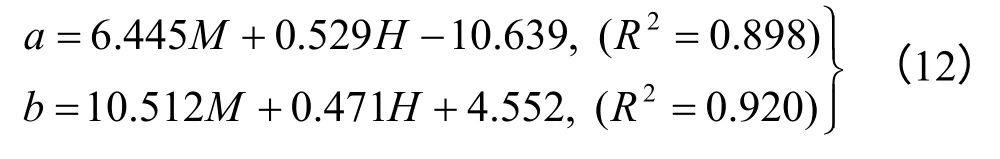
在能够预测震级的情况下，通过式（11）、（12）可以判断出穿越活断层的埋地隧道在走滑断层作用下的抗震薄弱部位，公式中考虑了基岩上覆土层厚度的影响，为实际工程中地铁隧道穿越地震断层的合理布置提供了参考依据。

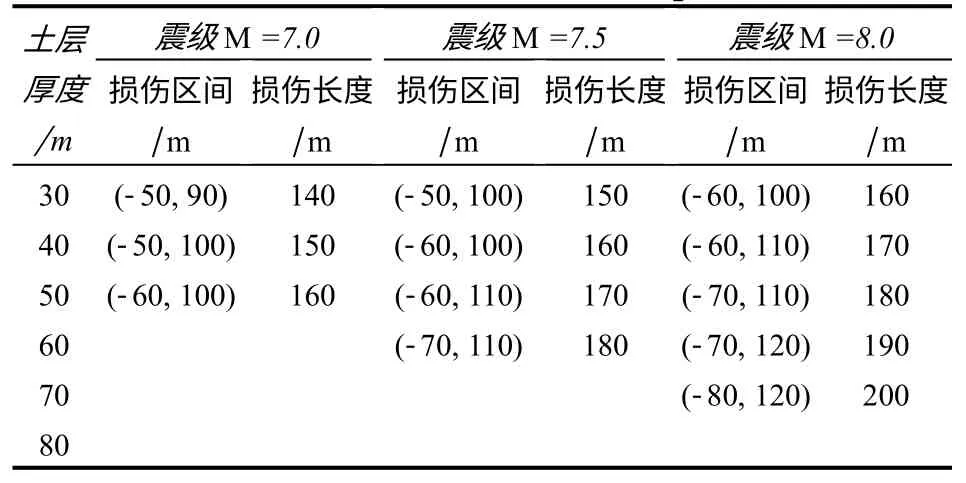
表6 走滑断层作用下衬砌结构损伤情况Table 6 Damage condition of lining structure under strike-slip

通过以上的分析可知，走滑断层位错作用下衬砌结构拱腰部位的损伤最为严重，不同土层厚度下拱腰部位的损伤分布如图8所示。图中，交线1指固定盘与断层破碎带的交线，交线2指活动盘与断层破碎带的交线。从图中可见，拱腰部位损伤最大值出现位置到交线1、2的距离随着土层厚度的增加而增大，而不是位于断层破碎带上方。在场地土均匀的情况下，左、右拱腰的损伤曲线呈反对称分布。分析图8数据发现，左、右拱腰处损伤最严重的位置分别到断层破碎带与固定盘和活动盘交线的距离W 与土层厚度H 之间呈线性增长关系，可以拟合为关系式（13），其相关系数R2=1.000，拟合曲线如图9所示。

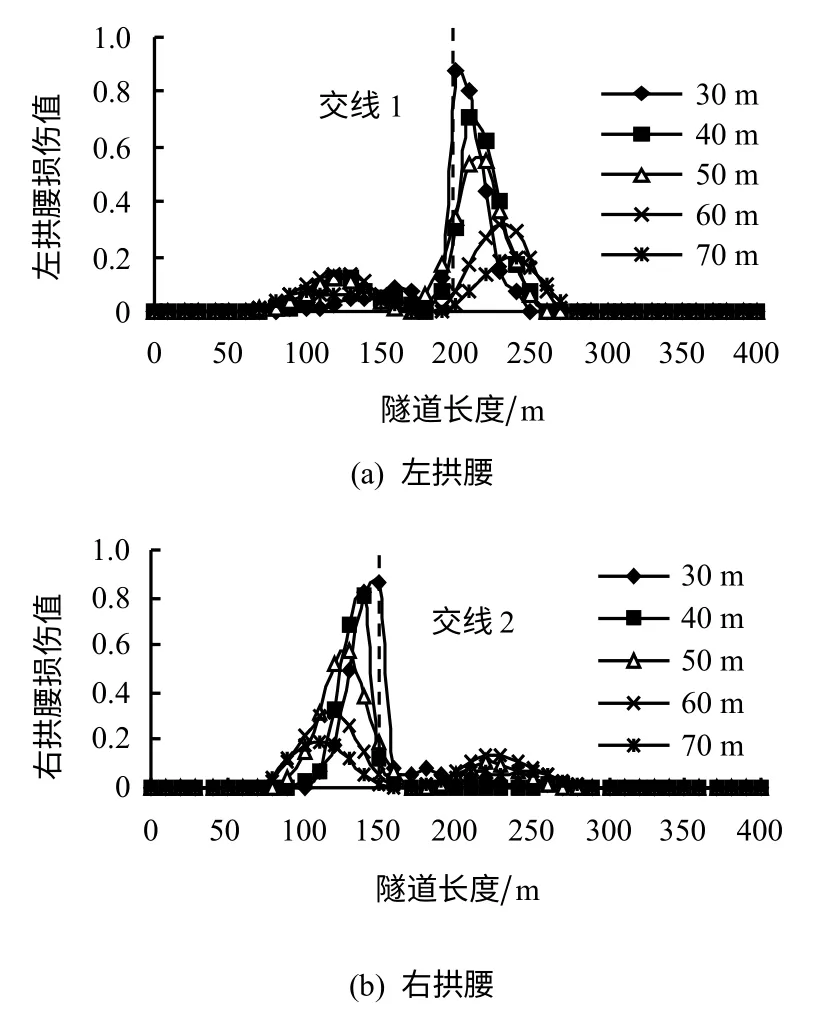
图8 不同土层厚度下拱腰损伤分布曲线Fig.8 The damage curves of hance under different soil thicknesses

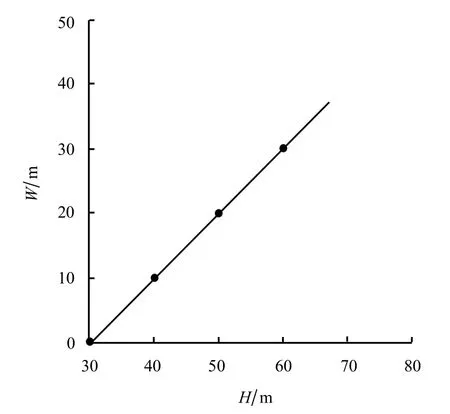
图9 W 与H 关系拟合曲线Fig.9 Fitting curve of relation between W and H

5 结论

（1）走滑断层位错作用下衬砌结构出现损伤的区域主要发生在断层破碎带上方及其附近一定范围内，拱腰部位的损伤最为严重，其次为拱底，拱顶处的损伤相对较轻。

（2）临界覆盖土层厚度H临界值与震级M 之间呈线性增长的关系，通过回归拟合的公式可估算出某一震级下所对应的临界覆盖土层厚度值。当基岩上覆土层厚度H≥H临界值时，可以不考虑走滑断层断裂对于浅埋隧道的影响。可见，随着基岩上覆土层厚度的增加，结构的震害程度逐渐降低。

（3）在走滑断层作用下衬砌结构的损伤区域长度与震级的大小和土层厚度有关。土层厚度一定时，震级越大，结构出现的损伤区域长度也越大。震级一定时，随着土层厚度的增加，结构发生损伤的区域长度逐渐增加，但损伤值逐渐减小。左、右拱腰处损伤最严重的位置分别到断层破碎带与固定盘和活动盘交线的距离W 与土层厚度H 之间呈线性增长关系。

（4）通过回归拟合出的关系式可快速判断出隧道结构在活断层作用下的抗震薄弱部位，对于穿越活断层地铁隧道的抗震设计具有一定的指导意义。

[1]刘晶波，李彬.地铁地下结构抗震分析及设计中的几个关键问题[J].土木工程学报，2006，39(6):106－110.LIN Jing-bo，LI Bing.Issues on the seismic analysis and design of subway structures[J].China Civil Engineering Journal，2006，39(6):106－110.

[2]KONTOGIANNI V A，STIROS S C.Earthquakes and seismic faulting:effects on tunnels[J].Turkish Journal of Earth Sciences，2003，12:153－156.

[3]ANASTASOPOULOS I，GEROLYMOSN，DROSOS V，et al.Behavior of deep immersed tunnel under combined normal fault rupture deformation and subsequent seismic shaking[J].Bulletin of Earthquake Engineering，2008，6(2):213－239.

[4]左娟花，林克昌.断层错动对上覆土体及隧道影响的模型试验[J].山西建筑，2012，38(23):56－58.ZUO Juan-hua，LIN Ke-chang.Model test research for the impact of underground tunnel by fault rupture[J].Shanxi Architecture，2012，38(23):56－58.

[5]张维庆.穿越断层隧道震害机理以及抗减震技术研究[D].成都:西南交通大学，2012.

[6]沈新普，王琛元，周琳.一个钢筋混凝土损伤塑性本构模型及工程应用[J].工程力学，2007，24(9):122－128.SHEN Xin-pu，WANG Chen-yuan，ZHOU Lin.A damage plastic constitutive model for reinforced concrete and its engineering application[J].Engineering Mechanics，2007，24(9):122－128.

[7]KARLSSON H，SORENSEN.ABAQUS standard user’s manual:ABAQUS 6.5 theory manual[M].Pennsylvania:Pennsylvania State Univesity，2005.

[8]王金昌，陈页开.ABAQUS在土木工程中的应用[M].浙江:浙江大学出版社，2006.

[9]张伟.大直径盾构隧道结构地震响应及减震措施研究[D].武汉:中国科学院武汉岩土力学研究所，2009.

[10]日本土木学会.隧道标准规范（盾构篇）及解说[M].朱伟译.北京:中国建筑工业出版社，2001.

[11]赵颖，郭恩栋，王琼，等.走滑断层地震地表断裂位错估计方法研究[J].岩土力学，2013，34(5):1403－1408.ZHAO Ying，GUO En-dong，WANG Qiong，et al.Estimate method of dislocation to seismic surface rupture under strike-slip fault[J].Rock and Soil Mechanics，2013，34(5):1403－1408.