天津软土地区盾构掘进对上方建筑物影响分析

姜晓婷，路 平，郑 刚，崔玉娇，崔 涛

（1.天津大学 滨海土木工程结构与安全教育部重点实验室，天津 300072；2.天津大学 建筑工程学院，天津 300072）

1 引言

目前在天津、北京、上海及广州等大城市中，大量历史建筑的存在对地下空间的开发提出了巨大的挑战，尤其是盾构隧道的开挖对邻近老旧历史建筑物的影响已经成为隧道工程发展所面临的亟需解决的重要课题。尤其是在软土地区，盾构隧道施工不可避免地扰动周围地层，进而引起地面沉降，沉降过大时将危及邻近建（构）筑物的结构安全。这些历史建筑建造年代长，且经受地震等灾害破坏，整体刚度差，对不均匀沉降的耐受能力极差。因此，当隧道周边存在老旧建筑物时，为了保证隧道施工的顺利进行及周边建筑物的安全，有必要对隧道开挖可能引发的邻近建筑物变形情况开展精细化分析。国内外学者在这方面做了很多研究。

于宁等[1]，许江等[2]建立了二维有限元模型分析了地铁盾构隧道对地上建筑物的影响。Mroueh等[3]，丁祖德等[4]，彭立敏等[5]利用可以考虑建筑物受力和变形空间效应的三维有限元方法，对地表有无建筑物的盾构掘进以及盾构掘进轴线与建筑物不同夹角的情况进行分析，分别研究了地面框架结构对地表沉降的影响以及隧道开挖对地表建筑物基础沉降和结构受力变形分布的影响。姜忻良等[6]以框架结构为研究对象，计算了盾构法地铁隧道穿越建筑物时对建筑物自身沉降和内力的影响，提出建筑物基础的沉降主要发生在地铁隧道穿越建筑物的区间段内。

上述研究主要集中于隧道施工对地表框架结构建筑物的影响程度和范围，而盾构隧道掘进对砌体结构建筑物的影响也有相关研究。Miliziano等[7]采用二维数值方法分析了隧道施工对某砖石结构建筑物的影响，得出了建筑物沉降曲线。葛世平等[8]通过理论研究的方法，分析了盾构穿越某砌体结构房屋时，施工期沉降以及后期固结沉降对房屋的影响。徐礼华等[9]，徐泽民等[10]通过隧道施工现场实测数据的分析，研究了隧道施工对地表砌体结构建筑物的影响。但目前针对软土地区下穿砌体结构的盾构掘进研究中，考虑盾构穿越引起的土体的应变在较大的范围内处于小应变状态的影响的研究相对较少。

本文结合天津地铁2号线盾构隧道下穿砌体结构建筑物的施工情况，采用现场监测和有限元模拟相结合的方法，研究隧道施工对地表砌体结构建筑物的影响。考虑隧道变形与建筑物变形的相互耦合关系，按照结构-土体-隧道共同作用进行分析。利用有限元软件Plaxis 3D建立三维非线性有限元模型，采用考虑土体小应变特性的土体本构模型对隧道与建筑变形进行分析，从而对隧道开挖所引发的邻近建筑物位移响应进行更为合理的预测。

2 工程概况

2.1 隧道及建筑物概况

天津地铁某盾构区间左线长度为533.504 m，共444环。右线长度为497.384 m，共415环。线路最大纵坡为19‰，最小纵坡为10.982‰，盾构隧道最小曲线半径为300 m，区间隧道覆土厚度约为17～21 m，未设置联络通道。采用海瑞克土压平衡盾构机，盾构外径为6.4 m，管片厚度为350 mm。管片拼装衬砌为单洞圆形隧道，采用错缝拼装，使用M30弯螺栓连接管片，环宽为1.2 m，管片混凝土为C50、S10；钢筋采用HRB335热轧钢筋、HPB235热轧钢筋。

盾构机于10月13日从始发端出发，进行右线的开挖，于10月19日到达建筑物前方30 m处，10月24日掘进至建筑物处，此时已掘进了47环，11月9日到达建筑物后方30 m处。

区间段下穿建筑物为4层砖混结构，各层层高为3 m，矩形平面，长29 m，宽13 m。建筑物基础为筏板基础，厚度为0.5 m，基础埋深为1.0 m。建筑物外观如图1所示。由于该建筑物已拟拆迁，故隧道下穿时并没有采取特别的保护措施，如特别调整、控制每环排土量及注浆量等，故通过建筑物时各施工参数与在空旷场地时相比相差不大。

建筑物所处路段隧道拱顶距地表平均约为19 m，建筑物距离隧道最小水平净距为0.81 m，位于隧道影响区内。为了监控隧道施工引起的地表不均匀沉降造成地表建筑物的破坏，本盾构区间隧道施工时，在建筑物基础底部沿长宽两个方向分别布设了基础沉降观测点（JG4-1～JG4-11），以监测建筑物各阶段的沉降以及不均匀沉降。另外，在建筑物前方较空旷的场地，也布设了地表沉降测点（DB8-8～DB8-17）以进行空旷场地的地表沉降槽的模拟。建筑物与隧道相对位置关系及建筑物监测点分布情况如图2。

图1 建筑物外观图Fig.1 Appearance of building

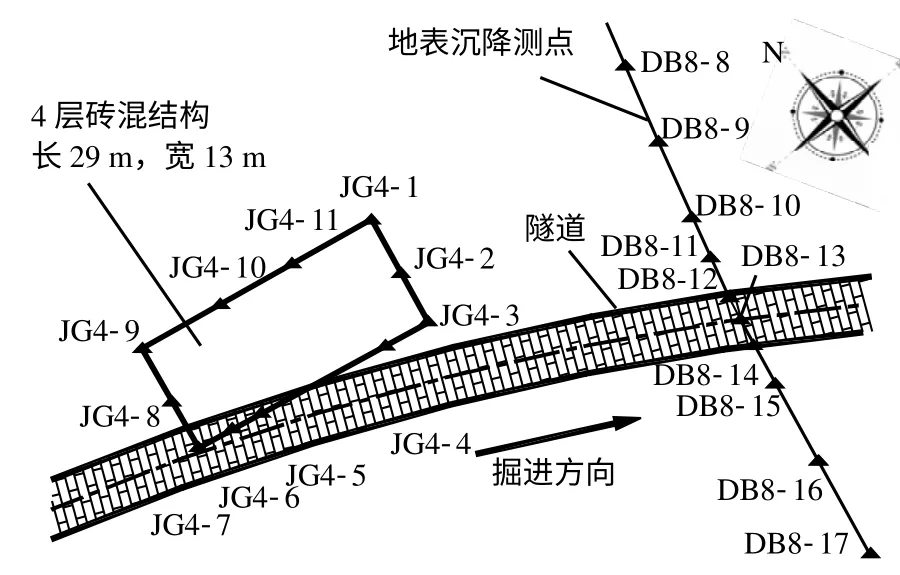
图2 建筑物与隧道相对位置关系及监测点分布Fig.2 Relative position between building and tunnel，and plan of monitoring instruments

2.2 场地条件概述

隧道穿越范围内主要有⑥2粉土、⑦2粉土层、⑥1⑦1粉质黏土、下部⑦4粉砂层，下部粉砂层厚度约10 m左右。场地内地下水位较高，勘测期间地下水埋深3.77～4.01 m。

3 有限元模型的建立

3.1 模型建立

采用Plaxis 3D 2013硬化土本构模型（HS）以及考虑小应变的硬化土本构模型（HSS）分别进行模拟。

建筑物与基础的网格划分情况如图3(a)所示。有限元模型整体网格划分情况如图3(b)所示，土体采用十节点四面体单元，共划分49 263个网格，85 399个节点。沿掘进方向的模型长度为90 m，垂直掘进方向长度取为96 m，竖直方向取50 m，隧道中心线埋深为22.5 m。盾构开挖步长定为3 m。盾尾注浆采用施加一环注浆压力（340 kPa）的方法进行模拟。

模型的边界条件如下：模型顶面为自由面，无约束；模型底面约束法向位移；模型四个侧面均只约束法向，其余方向自由无约束。本文重点研究盾构掘进对土体的短期影响，不考虑长期固结。

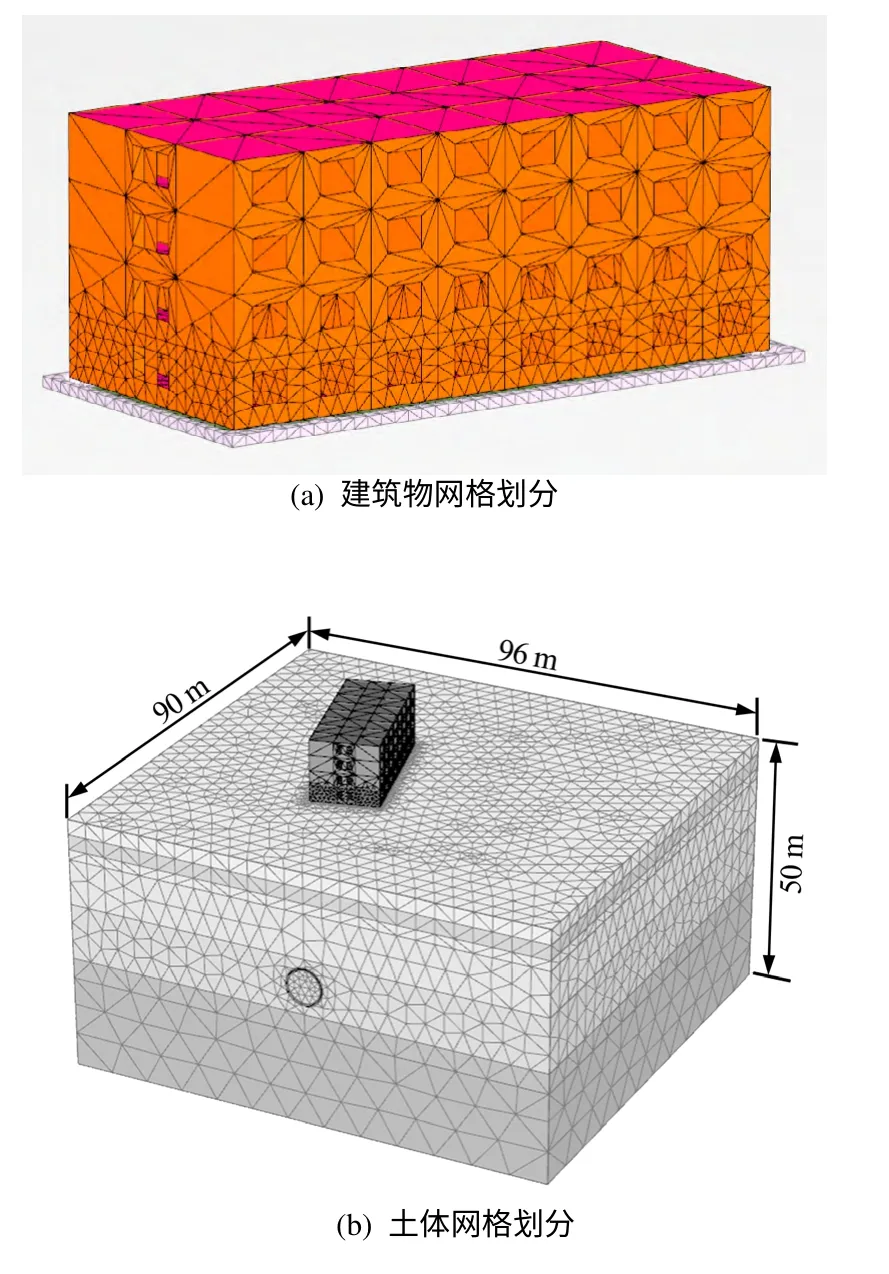
图3 有限元模型网格划分Fig.3 Finite element model and meshes

3.2 模型参数

（1）土层参数

土体的本构模型采用考虑了小应变刚度行为的硬化土模型（harding-soil small，HSS），即在硬化土模型（hardening-soil，HS）的基础上考虑了土体的小应变刚度特性。土体的模型参数的确定通过盾构区间所在的天津软土地区典型土体的多处钻孔勘察报告结果及室内试验得出。土体的分层及参数如表1所示，小应变本构模型参数是在硬化土本构模型参数的基础上增加初始剪切模量G0和剪切应变水平 γ0.7两个参数，γ0.7为G0衰减至70%时的应变水平，γ0.7取0.000 2[11－12]。

（2）建筑物与盾构掘进参数

建筑物门窗孔洞尺寸为1.8 m×1.5 m和0.9 m×1.5 m。建筑物具体尺寸如图4所示。

图4 建筑物尺寸示意图(单位:mm)Fig.4 Sketch of the building dimensions(unit:mm)

模型考虑了建筑物的横墙、纵墙以及楼板，而不考虑梁、柱的影响。楼板和墙体均按理想弹塑性模型的板单元进行考虑。砌体规范[13]中规定，普通砖砌体结构的弹性模量取值范围为1.5～6.0 GPa（当砖砌块强度等级达到MU30，同时砂浆强度等级达到M15时，其弹性模量才可以取大值），而在砌体结构遭受地震荷载作用，在其内部发生损伤或者开裂时，建筑结构的整体刚度将发生急剧下降[14]。因此，本文中取墙体的弹性模量为220 MPa，泊松比为0.1[15]，墙体厚度取为240 mm。楼板厚度取120 mm，弹性模量为30 GPa，泊松比为0.2。建筑物基础为筏板基础，基础采用线弹性模型，基础厚度为0.5 m，弹性模量为30 GPa，泊松比为0.2。

盾构机机身及管片单元采用板单元进行模拟。管片按整体结构进行计算，但对管片采用0.75的刚度有效率[16]来考虑管片错缝拼接的影响，弹性模量取26 GPa，泊松比为0.2，重度为25 kN/m3。盾构机机身外径为6.4 m，厚度为100 mm，弹性模量取240 GPa，泊松比为0.2。实际工程中，隧道周围的土体实际上会产生偏向隧道轴线下方的不均匀收缩，并且根据Plaxis帮助文件[17]中的实例，将盾构机机身的重度取为120 kN/m3。

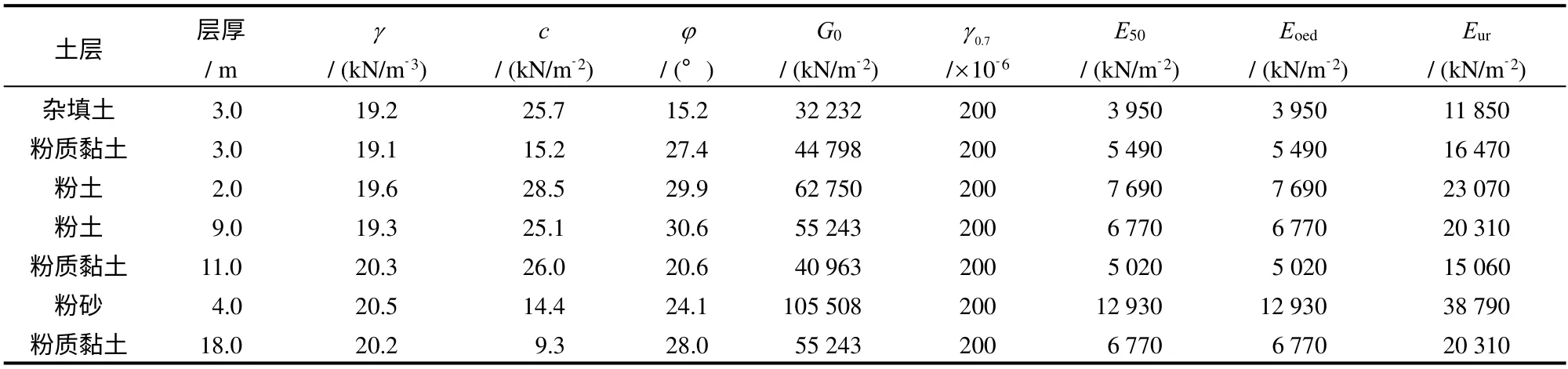
表1 土体分层及物理力学指标Table 1 Soil strata and physical and mechanical properties

3.3 小应变本构

大量试验研究结果表明，土体的应变对土体刚度会产生十分显著的影响[18－19]。当土体发生小应变的时候，土体的刚度会远远高于常规试验得到的刚度。国内大量研究认为，在施工过程中，隧道、基坑以及基础周围除了少数区域发生塑性外，其他大部分区域的土体处于小应变的状态（0.01%～0.3%）[20]，如图5所示。

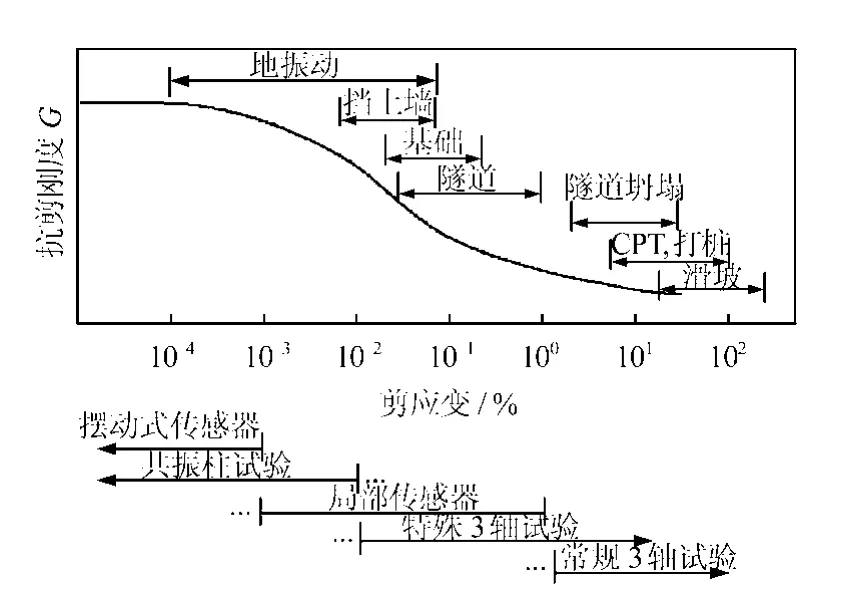
图5 土体在各种岩土工程条件下的应变范围Fig.5 Strain range of soil in variety of conditions of geotechnical engineering

在小应变条件下的土体会表现出高模量、非线性以及模量衰减性。Rowe等[21－22]指出，利用各向同性弹性－理想塑性的土体本构模型得到的地面沉降槽的宽度要比实测数据地面沉降槽宽得多，因此，如何反映小应变下土体的固有特性对能否正确预测地下工程施工对周围环境的影响起到至关重要的作用。因此，开展精细化分析，考虑土体的小应变特性是十分必要的。

4 天然地表（无建筑物）沉降变形

为了考虑土体小应变特性的影响，本文采用了plaxis 3D中的HSS本构模型，并将其与不考虑小应变特性的HS模型进行对比。同时，为了验证HSS模型的可靠性，本文选取了盾构到达建筑物前的空旷场地区段进行模拟。将该区段内的计算沉降曲线与相应位置的实测沉降槽（DB8-13）曲线进行对比，如图6所示。

图6 模型计算结果与现场实测值对比Fig.6 Comparison of the calculation results and measurement results

可以看出，考虑小应变影响的HSS模型计算得出的结果曲线与实测结果较为吻合，而HS模型得出的沉降曲线与实测结果差异较大。沉降槽宽度系数i 可近似取为0.6倍的最大地表沉降值处所对应的点距隧道轴线的距离[23－24]。则HS模型i 值为15.1 m，HSS模型i 值为13.5 m。无论是最大沉降值还是沉降槽宽度，HS模型均显著大于HSS模型计算结果及现场实测值，这将直接影响盾构从侧下方穿越建筑物时的数值分析结果。文献[23]中，将HS模型、HSS模型以及实测结果的沉降槽宽度进行对比，本文所得出的结论与该文相关的规律是一致的。

5 盾构掘进对建筑物的影响分析

5.1 建筑物变形监测

本盾构区间对建筑物变形的监测包括：建筑物基础沉降监测、倾斜监测。

多层砌体建筑物与隧道相对位置关系及建筑物基础的监测点布置如图2所示。分别对盾构区间隧道下穿施工时建筑物沉降监测值随观测时间的变化情况进行分析，如图7所示。

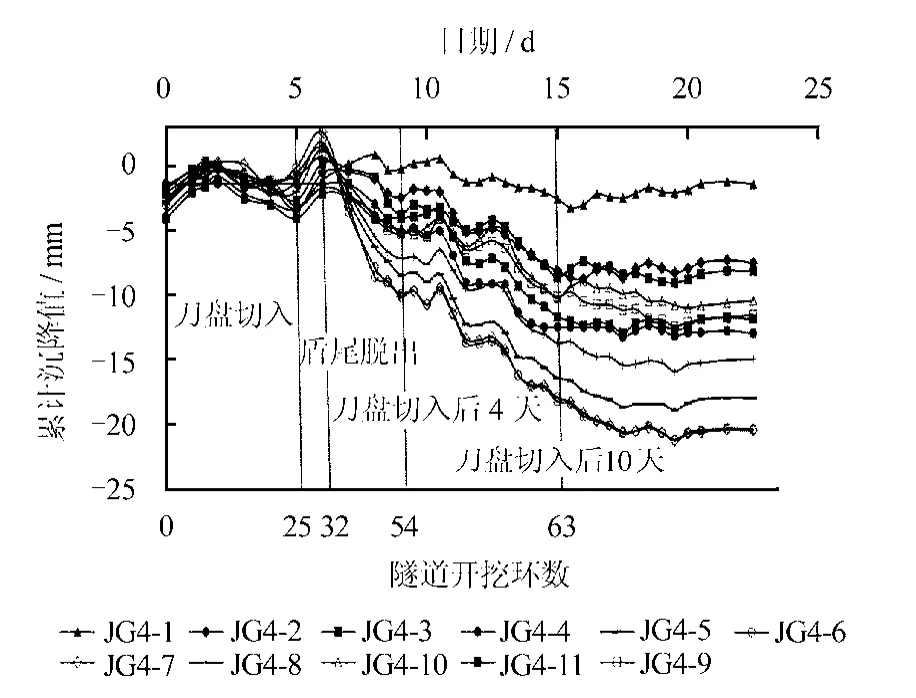
图7 实测建筑物监测点的沉降时程曲线Fig.7 Measured settlement-time curves of building

建筑物的基础沉降值在刀盘刚切入建筑物后有轻微的隆起，最大隆起量为2.6 mm。随着隧道开挖，各测点逐渐沉降，沉降值随着时间推移不断增大，在盾尾脱出10天之后，各测点沉降趋于稳定。从图7还可以明显看出，测点JG-7与JG-6沉降速率和沉降累计值都比其他各点要大，这与该测点与隧道轴线的距离较近有关，也从另一方面说明隧道开挖引起的建筑物基础沉降规律与地表沉降规律有一定的相关性。建筑物监测点的沉降变化规律及最大沉降值与文献[25]所得到的结论相一致。

5.2 建筑物不均匀沉降监测

建筑物的不均匀沉降可用差异沉降δ 或斜率k表示，其中k=δ/L，L为两沉降测点之间的距离。远离隧道轴线方向的倾斜斜率定义为正，偏向隧道轴线方向的倾斜斜率定义为负。

建筑物沿纵向不均匀沉降通过监测北立面JG4-1、JG4-11、JG4-10、JG4-9以及南立面JG4-3、JG4-4、JG4-5、JG4-6、JG4-7沉降点获得。建筑物沿横向不均匀沉降通过监测东山墙JG4-1、JG4-2、JG4-3以及西山墙JG4-9、JG4-8、JG4-7沉降点获得。

如图8所示，为建筑物随着盾构掘进的过程中，南立面、北立面、东山墙以及西山墙的斜率随开挖时间变化而变化的过程。在盾构到达之前，建筑物的沉降较为均匀，只有轻微的倾斜。刀盘切入时，建筑物向远离隧道的方向倾斜，可能是由于掌子面推力引起的盾构前方土体隆起导致的。盾尾脱出后，建筑物向隧道中心线方向倾斜，且建筑物的倾斜斜率变化较快，至刀盘切入后4天，变化速率稍有减缓，至刀盘切入后10天，建筑物倾斜斜率基本稳定。图中东山墙的最终斜率最高，为0.9‰。

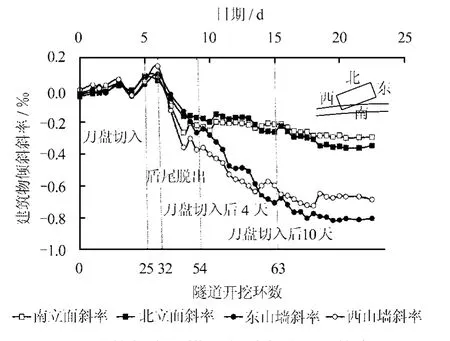
图8 建筑物实测横纵向斜率随时间的变化Fig.8 Transverse and longitudinal slope of buildings varied with time

5.3 现场监测结果与有限元结果的对比

选取建筑物中最靠近隧道中心的沉降点JG4-7，将HSS模型得到的结果与现场实测以及HS模型得到的结果进行对比，如图9所示。

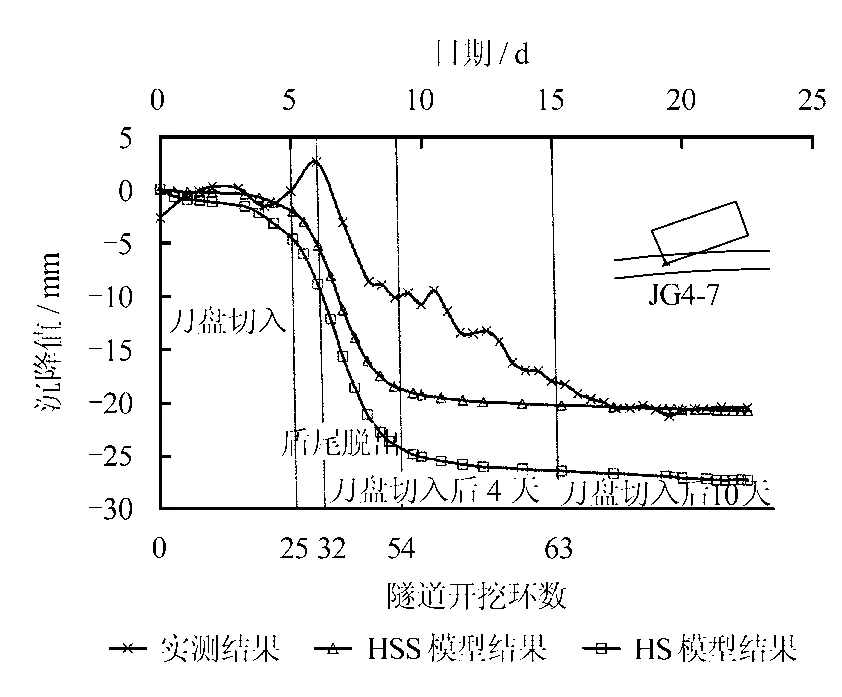
图9 监测点JG4-7随盾构掘进的沉降时程曲线Fig.9 The settlement-time curves of JG4-7 during the tunneling

可以看出，JG4-7监测点实测最大沉降值为21.2 mm，由HSS模型计算出的最大沉降值为20.7 mm，而HS模型计算出的最大沉降值为27.3 mm，考虑小应变的HSS模型计算出的最终沉降值与实测结果吻合的较好，而HS模型的最终沉降值偏大。

实测沉降时程曲线在刀盘切入之后有轻微隆起，最大隆起量为2.8 mm，这是由于掌子面对前方土体的推力以及盾构机身侧壁对土体的摩擦力使土体超孔压且来不及消散，导致土体轻微隆起；而HSS计算模型在刀盘切入之后土体沉降开始变大，没有隆起的现象产生，这是由于有限元模拟的过程中，暂时没有考虑孔压缓慢消散的过程，所以沉降发展较快，与实测曲线略有差异，但最终沉降值基本吻合。所有监测点的实测最终沉降值与HSS模型得到的最终沉降的对比如表2所示。

表2 监测点沉降对比Table 2 Comparison of predicted and measured settlement

由表2可看出，除点JG4-1外，其余各测点沉降的实测数据与小应变有限元计算数据均相差较小。并且靠近隧道上方的点的沉降值相差不到1 mm，从而验证了计算结果的准确性。

本文将建筑物4个面的最大倾斜量进行计算，并和实测数据对比来进一步研究建筑物的倾斜。对比结果如表3所示。

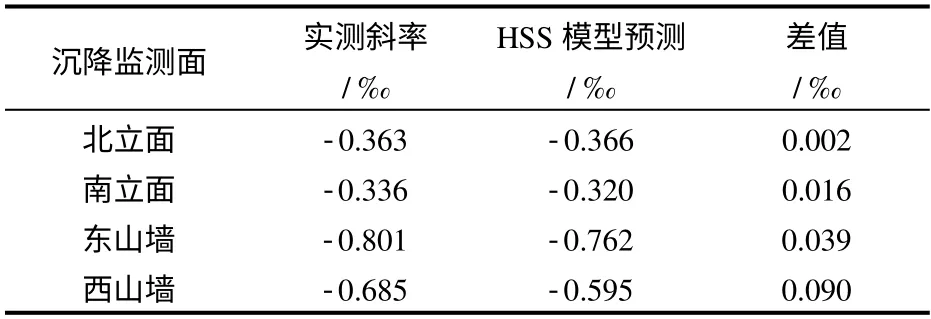
表3 建筑物倾斜斜率对比Table 3 Comparison of predicted and measured building inclination

HSS本构模型计算出来的建筑物不均匀沉降结果与实测的建筑物倾斜拟合较好，差值控制在0.1‰以内，说明有限元计算出的建筑物的倾斜值较为准确。

如图10所示，本文选取建筑物的东西山墙的倾斜沉降进行分析，小应变模型结果与实测结果的对比如下图所示。图中曲线表示建筑物各边倾斜斜率随着盾构掘进的变化情况。

图10 东西山墙的倾斜斜率随时间的变化Fig.10 Tilt of building gable wall varied with time

由图10中可以看出，东西山墙倾斜斜率变化趋势与实测数值略有差异，实测数值的斜率是缓慢平稳地增大的，至刀盘切入后15 d达到稳定。而有限元模型的斜率是在刀盘切入后开始迅速增大，至刀盘切入后五天逐渐达到稳定状态。虽然最终结果差异不大，但是由斜率变化的趋势可以推断出，实际的土体是缓慢变形的，随着孔隙水压力的逐渐消散，缓慢的发生不均匀沉降。而有限元模型计算出的斜率在刀盘切入后迅速发生。尽管在HSS本构模型中，本文考虑了盾构掘进时间以及固结的影响，但是有限元模型中孔隙水压力的消散发生的时间较短，使土体很快达到固结，进而建筑物的沉降（见图9）以及倾斜斜率（见图10）都发生在很短的一段时间内，与实际工程略有差异。

6 盾构掘进关键参数敏感性分析

由于盾构穿越图2所示建筑物及DB8-13后，将下穿京津城际铁路，并要求下穿时的铁路沉降小于8 mm。即在地面荷载、土质条件基本保持不变时，要将盾构下穿路基时，引起的地面最大沉降由DB8-13处的约18.5 mm减小为8 mm。因此，基于图6所示的空旷场地条件下的数值模拟，研究通过调整盾构掘进关键参数，实现将地面沉降控制在更小值的要求，并考虑参数调整时盾构相对于沉降控制点的位置的影响。

图11(a)所示为改变同步注浆压力P 时，地表沉降δ 的变化趋势。由图可看出，地表绝对沉降值会随着注浆压力P 的增大而减小。而在盾构机到达之前，地表发生轻微的隆起，且隆起量会随着注浆压力的增大而略有增加。图11(b)所示掌子面推力F（图中F 以埋置深度z为单位，即分别为12z，14z和16z，kPa）的变化引起地表沉降δ 的变化情况。随着掌子面推力的增大，地表绝对沉降值随之减小，但减小的幅度较小。主要是由于掌子面推力在掘进过程中能够维持盾构前方土体的稳定性，本文隧道埋深较大，对地表沉降的影响并不明显。如图11(c)所示，随着土体损失率的增大，地表沉降δ 会随之增大，且变化较为明显。

图11 盾构掘进各阶段地表沉降随掘进参数的变化曲线Fig.11 Variation of the ground settlement with driving parameters for all tunneling stages

综合以上3种情况的分析，在本文所取参数变化较为合理的工况下，所分析的各个参数对地表沉降的影响按从强到弱的顺序依次为：土体损失率、注浆压力、掌子面推力。

7 结论

（1）通过对地表沉降监测点的空旷场地模拟，可以看出，HSS模型计算得到的沉降槽宽度与实测曲线一致，且要比HS模型的沉降槽宽度窄。

（2）通过空旷场地以及隧道下穿建筑物的模拟可知，考虑小应变本构模型的HSS模型计算得到的地表最大沉降值以及建筑物基础最大沉降值也与实测拟合良好，而不考虑土体小应变的硬化土HS模型最终沉降值较大。

（3）建筑物的不均匀沉降在盾构到达之前较为均匀，只有轻微的倾斜。刀盘切入时，建筑物向远离隧道的方向倾斜。盾尾脱出后，建筑物向隧道中心线方向倾斜，且倾斜斜率变化较快。

（4）HSS模型计算出来的建筑物不均匀沉降结果与实测的数值拟合良好，差值控制在0.1‰以内。

[1]于宁，朱合华.盾构施工仿真及其相邻影响的数值分析[J].岩土力学，2004，25(2):292－296.YU Ning，ZHU He-hua.The simulation of shield tunnel construction and analysis of its influence upon surrounding environments[J].Rock and Soil Mechanics，2004，25(2):292－296.

[2]许江，顾义磊，康骥鸣.隧道与地表构筑物相互影响的研究[J].岩土力学，2005，26(6):889－892.XU Jiang，GU Yi-lei，KANG Ji-ming.Study of interaction of tunnel and upper structure[J].Rock and Soil Mechanics，2005，26(6):889－892.

[3]MROUEH H，SHAHROUR I.A full 3-D finite element analysis of tunneling–adjacent structures interaction[J].Computers and Geotechnics，2003，30(3):245－253.

[4]丁祖德，彭立敏，施成华.地铁隧道穿越角度对地表建筑物的影响分析[J].岩土力学，2011，32(11):3387－3392.DING Zu-de，PENG Li-min，SHI Cheng-hua.Analysis of influence of metro tunnel crossing angles on ground buildings[J].Rock and Soil Mechanics，2011，32(11):3387－3392.

[5]彭立敏，丁祖德，黄娟，等.隧道穿越方式对地表建筑物变形影响的数值分析[J].中南大学学报(自然科学版)，2012，43(1):308－314.PENG Li-min，DING Zu-de，HUANG Juan，et al.Numerical analysis of deformation influence of tunnel crossing types on ground building[J].Journal of Central South University (Science and Technology)，2012，43(1):308－314.

[6]姜忻良，贾勇，赵保建.地铁隧道施工对邻近建筑物影响的研究[J].岩土力学，2008，29(11):3047－3052.JIANG Xin-liang，JIA Yong，ZHAO Bao-jian.Analysis of influence of metro tunnel construction on adjacent buildings[J].Rock and Soil Mechanics，2008，29(11):3047－3052.

[7]MILIZIANO S，SOCCODATO F M，BURGHIGNOLI A.Evaluation of damage in masonry buildings due to tunneling in clayey soils[C]//Geotechnical Aspects of Underground Construction in Soft Ground in 3rdInternational Symposium.[S.l.]:[s.n.]，2002:49－54.

[8]葛世平，廖少明，陈立生.地铁隧道建设与运营对地面房屋的沉降影响与对策[J].岩石力学与工程学报，2008，27(3):550－556.GE Shi-ping，LIAO Shao-ming，CHEN Li-sheng.Influence of construction and operation of metro tunnel on settlement of ground buildings and countermeasures[J].Chinese Journal of Rock Mechanics and Engineering，2008.27(3):550－556.

[9]徐礼华，艾心荧，余佳力.厦门机场路隧道施工对砌体结构建筑物的影响分析[J].岩石力学与工程学报，2010，03:583－592.XU Li-hua，AI Xin-ying，YU Jia-li.Analysis of impact of tunnel construction on masonry buildings in Xiamen airport road[J].Chinese Journal of Rock Mechanics and Engineering，2010，03:583－592.

[10]徐泽民，韩庆华，郑刚.地铁隧道下穿历史风貌建筑影响的实测与分析[J].岩土工程学报，2013，35(2):364－374.XU Ze-min，HAN Qing-hua，ZHENG Gang.Field monitoring and analysis of effects of metro tunnels under historical buildings[J].Chinese Journal of Geotechnical Engineering，2013，35(2):364－374.

[11]BRINKGREVE R B J，SWOLFS W M，BEUTH L，et al.Plaxis 3D foundation material models manual[M].2nd ed.Delft:PLAXIS bv，2007.

[12]VERMEER P A.Small-Strain stiffness of soils and its numerical consequences[M].Stuttgart:Thomas Benz，2007.

[13]中华人民共和国建设部，国家质量监督检验检疫总局.砌体结构设计规范GB 50003－2001[S].北京:中国建筑工业出版社，2002.

[14]杜永峰，闫力.砌体结构地震损伤的识别及试验研究[C]//第四届全国防震减灾工程学术研讨会.福州:[s.n.]，2008:661－666.

[15]郑刚，李志伟.基坑开挖对邻近任意角度建筑物影响的有限元分析[J].岩土工程学报，2012，34(4):615－624.ZHENG Gang，LI Zhi-wei.Finite element analysis of response of buildings with arbitrary angle adjacent to excavations[J].Chinese Journal of Geotechnical Engineering，2012，34(4):615－624.

[16]黄宏伟，徐凌，严佳梁.盾构隧道横向刚度有效率研究[J].岩土工程学报，2006，28(1):11－18.HUANG Hong-wei，XU Ling，YAN Jia-liang.Study on transverse effective rigidity ratio of shield tunnels[J].Chinese Journal of Geotechnical Engineering，2006，28(1):11－18.

[17]BRINKGREVE R B J，SWOLFS W M，ENGIN E.Plaxis 3D tutorial manual version 2013[M].Delft:PLAXIS bv，2013.

[18]MAIR R J.Developments in geotechnical engineering research:applications to tunnels and deep excavations[C]//Proceedings of the Institution of Civil Engineers.London，1993.

[19]ATKINSON J H.Non-linear soil stiffness in routine design[J].Geotechnique，2000，50(5):487－508.

[20]MITCHELL J K，SOGA K.Fundamentals of soil behavior[M].3rd ed.Hoboken:John Wiley and Sons，2005.

[21]LEE K M，ROWE R K.Effects of undrained strength anisotropy on surface subsidences induced by the construction of shallow tunnels[J].Canadian Geotechnical Journal，1989，26(2):279－291.

[22]LEE K M，ROWE R K.Deformations caused by surface loading and tunneling:The role of elastic anisotropy[J].Geotechnique，1989，39(1):125－140.

[23]MATHEW G V，LEHANE B M.Numerical back-analyses of greenfield settlement during tunnel boring[J].Canadian Geotechnical Journal，2013，50(2):145－152.

[24]PECK R B.Deep excavations and tunneling in soft ground[C]//Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering.Mexico City:State of the Art Volume，1969:225－290.

[25]康鹏，杜一鸣，周印堂.天津地铁盾构施工中古旧建筑物的保护[J].建筑科学，2012，增刊1:262－266.