白山抽水蓄能泵站地下厂房的岩体力学参数反演

田泽润，李守巨，于 申

（大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116204）

1 引言

在岩土工程中确定岩体力学参数的主要方法有室内试验法、现场原位测试法、经验估算类比法和位移反分析方法，其中位移反分析法在岩土工程中被广泛应用，并发展出了多种反分析方法，如逆反分析法、正反分析法等[1－2]。这类方法可以适用于各种线性和非线性问题，通过以工程现场测量的位移数据为基础反求出岩体力学参数、初始地应力场等。数值计算方法在位移反分析中不同的实现形式又可以分为逆解法、直接法和图谱法。直接法利用各种优化算法（拟梯度法、单纯形法等）将参数反演问题转化为求目标函数最优解的问题[3]。由于传统优化算法的局限性，智能优化方法如粒子群算法、遗传算法等被广泛应用在反问题的研究中。

Javadi等采用遗传算法进行了岩土工程的反分析研究[4－5]。Monmarche等[6]采用蚁群算法及粒子群算法展开岩土工程反演研究，提高了反演算法的效率。李宁等[7－8]在漫湾水电站边坡以及华盛顿地铁的位移反分析中首次提出了考虑施工过程，施工方法影响的仿真反分析的思路。叶飞等[9]根据最优化反演分析的开尔文模型进行隧道岩体力学参数的反演分析。朱合华等[10]在遗传算法的基础上，发展了遗传算法与阻尼最小二乘法的耦合算法——混合遗传算法，并应用与位移反分析。冯夏庭等[11]结合人工神经网络和遗传算法，提出了进化神经网络方法。高玮等[12]采用优化计算效率更高的粒子群优化算法进行反分析研究，提出了粒子群优化反分析。高玮等[13]结合免疫系统原理及进化规划机制提出了新型仿生算法。

地下工程开挖过的程数值分析一般采用有限元法进行模拟。Karakus等[14]采用有限元数值方法模拟了地下隧道开挖过程中的应力释放过程，建立了Drucker–Prager破坏准则和顺序开挖模拟模型。陈帅宇等[15]采用了三维快速拉格朗日法（FLAC3D），模拟施工开挖过程，研究了复杂地质条件下洞室群围岩的开挖变形形态与应力。赖跃强等[16]采用地质力学模型平面应变实验技术，模拟彭水枢纽地下厂房洞室的构造特点和力学性能，分析研究了主厂房开挖过程中围岩的应力及洞室围岩的破坏机制。Tezuka等[17]系统地分析了日本大跨度地下厂房围岩稳定性分析地最新进展，介绍了几个比较典型的抽水蓄能泵站工程地下厂房开挖过程中围岩剪应力分布，标准的支护模式和反演分析结果。徐平等[18]采用三维弹塑性有限元法模拟了开挖过程，分析了围岩塑性区分布以及地下洞室群围岩的稳定性。李宁等[19]利用数值分析软件FINAL对乌江思林水电站地下厂房进行数值模拟，研究了围岩力学参数及该水电站地下厂房的初始应力场。本文基于变形观测数据和响应面法，提出了估计地下厂房岩体力学参数的位移反分析方法，通过观测变形数据和预测变形数据的对比，验证了本文方法的有效性。

2 工程概况

白山抽水蓄能泵站建于1975-1983年，位于第二松花江上游左岸。该电站利用已建的红石水库做下库，白山水库做上库，是我国目前最大的抽水蓄能工程。地质情况：山体标高490～510 m，地形坡度为25°～35°，区内河谷不甚发育，切割不深，地形较完整。区内露出的地层主要为前震旦系混合岩，山顶分布有第四系玄武岩混合岩致密坚硬，抗风化能力强。白山泵站地下厂房宽24.5 m，高50 m，长69 m，分6层进行开挖，第1～6层高程为▽300.6～▽291.1～▽282.66～▽275.1～▽266～▽257～▽250 m。为了监测厂房开挖过程中围岩位移的变化分别在拱肩、拱顶和边墙安装了多点位移计，见图1。

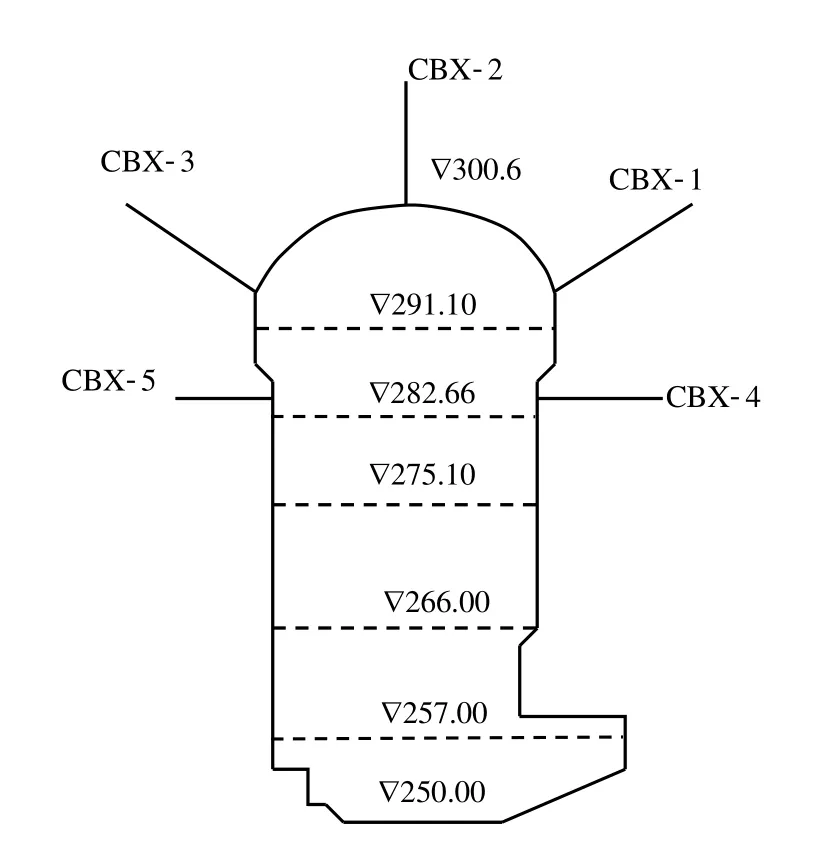
图1 地下厂房轮廓以及多点位移计的布置（单位：m）Fig.1 Cavern contour of powerhouse and arrangement of displacement meter(unit:m)

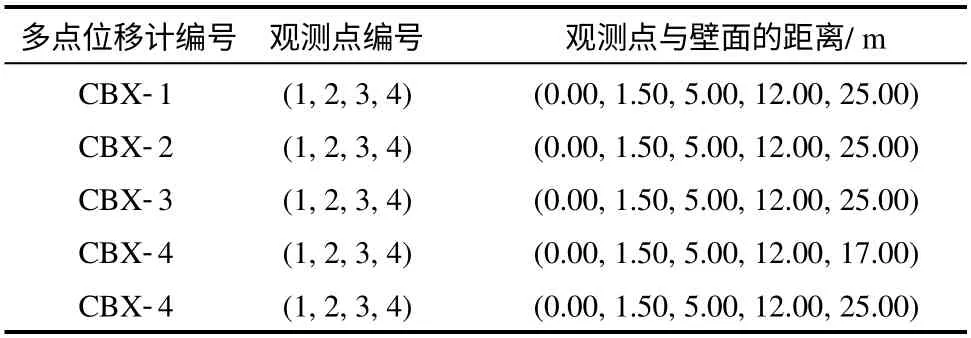
表1 多点位移计测点布置Table 1 Arrangement of measuring points

3 反演围岩力学参数的方法

3.1 参数反演问题的响应面

地下厂房的岩体力学参数同厂房开挖引起的变形之间存在一定的非线性关系，而多项式响应面方法作为设计优化中最为常用的一种代理模型近似方法可以建立这种非线性关系，响应面函数为

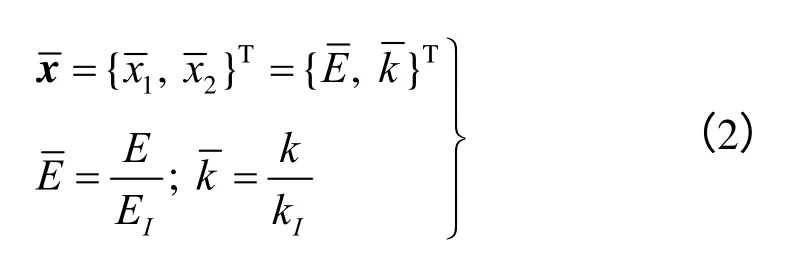
式中：EI、kI分别为弹性模量和侧压力系数的初始估计值，EI=40 MPa，kI=1.0。选取表2中的各种参数组合进行有限元正演分析，可以得到所有观测点位移数据，结合方程式（1）求解线性方程组，即可求出方程式（1）中未知的系数。

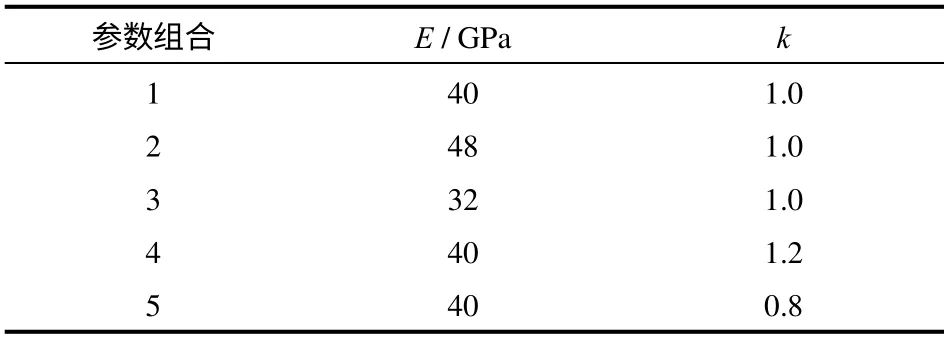
表2 弹性模量E 和测压力系数k 的不同参数组合Table 2 Parameter combinations of E and k

以第一个观测点（CBX-1-1）为例，以下方程的右边项可以采用有限元数值方法计算出：

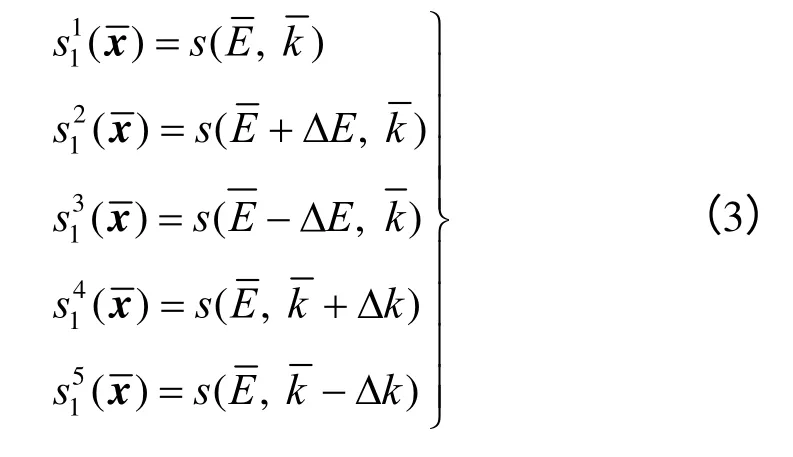
式中：ΔE为无量纲化的弹性模量，ΔE=0.2；Δk为应力比的增量，Δk=0.2；为观测点1在参数组合i 下的位移，通过有限元算出。5个方程中有5个未知系数，求解线性方程组，即可确定响应面函数的未知系数。

3.2 有限元数值模拟

为了模拟地下厂房的开挖过程，假设构造应力随深度线性分布，有限元模型左右边界施加水平荷载，如图2所示。

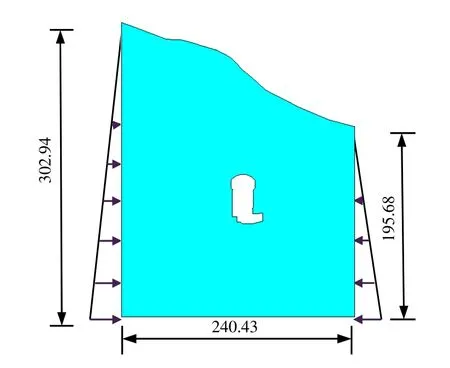
图2 地下厂房有限元模型（单位：m）Fig.2 Finite element model of underground powerhouse and rock mass(unit:m)

有限元模型的左右边界水平荷载：

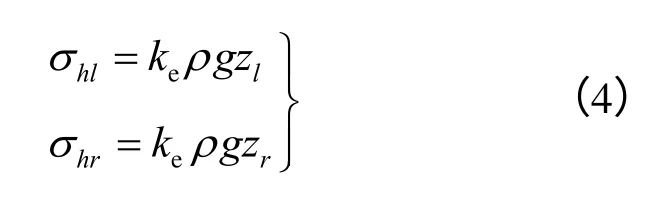
式中：ke为侧压力系数；zl、zr分别为左右边界高度；ρ为岩体密度；g为重力加速度。

选取表2中各参数组合，对地下厂房开挖过程进行数值模拟，可以得到各个观测点处的位移。仍然以观测点1为例，各组合参数对应的开挖变形见表3，表中M为观测次数。

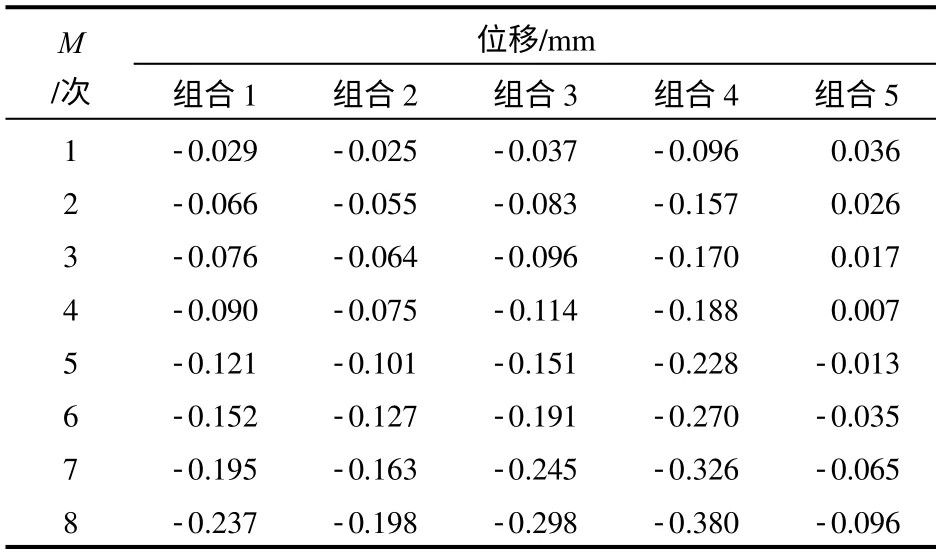
表3 观测点1在各参数组合下的开挖变形Table 3 Excavation deformation of observing point 1 in every parameter combination

观测点1有8个响应面函数，每个响应面函数有5个未知系数。根据表3和线性方程组式（3），可以求解出40个响应面函数的系数，见表4。

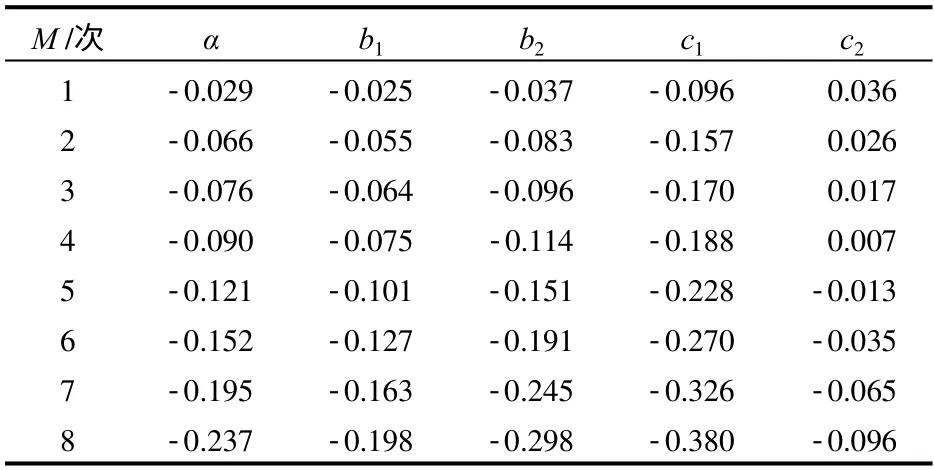
表4 观测点1的响应面系数Table 4 Response surface coefficients of observing point 1

利用Matlab软件画出观测点1在第一次观测时的响应面空间几何图形如图3所示。

用同样的方法可以计算出其他观测点共120个响应面函数系数。为了反演确定地应力场参数，在地下厂房布置3个观测点，每个观测点分别进行了8次变形观测，共有24个变形观测数据。分别采用了拟牛顿优化算法和遗传算法进行了地应力场参数反演，当24个用响应面函数预测位移与其观测值残差平方和达到极小值时，响应面函数中的自变量就是反演的地应力场参数。

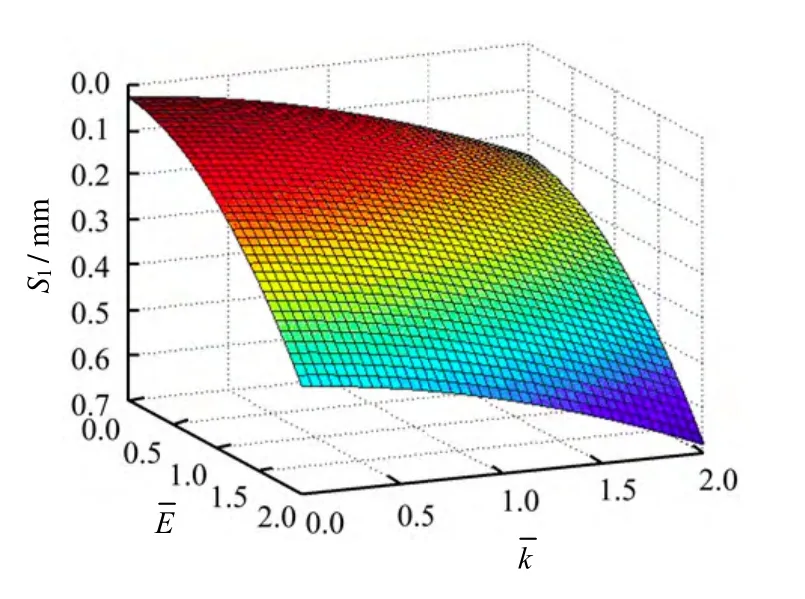
图3 观测点1的响应面空间分布Fig.3 Distribution of response surface function of observing point 1

3.3 参数反演的最优化求解

定义目标函数J，将参数反演问题转化为优化问题：

选取5组岩土力学参数的初始估计值，采用拟牛顿法进行目标函数最优化计算，参数反演结果见表5。

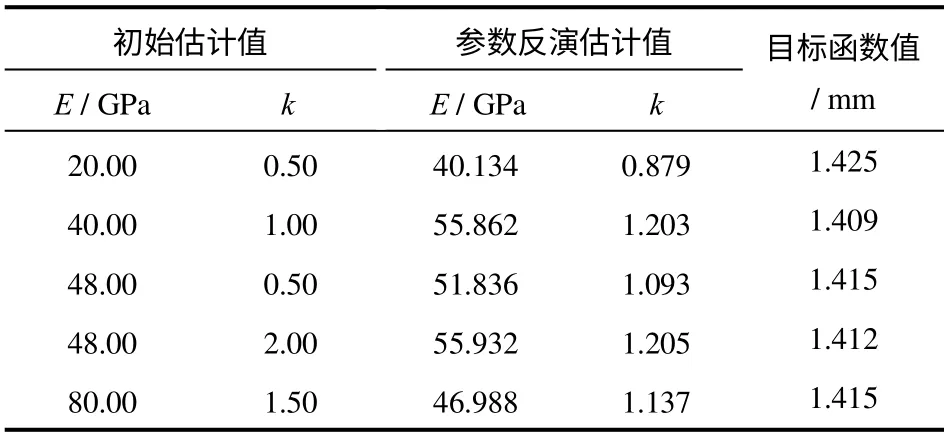
表5 不同初始估计值下的反演结果Table 5 Inversion results of different initial parameters

考虑到拟牛顿法可能取得局部极小值，利用遗传算法进行参数反演。初始种群数目为100，交叉概率设定为0.8，变异概率为0.05，进化51代后，得到全局近似最优解，见表6。

表6 遗传算法反演结果Table 6 Inversion results calculated by genetic algorithm

对比表5和表6可知，当岩土力学参数初始估计值E=40.00 GPa，k=1时，拟牛顿法的反演结果和遗传算法反演结果基本一致。

根据反演后的弹性模量和侧压力系数利用有限元数值方法模拟地下厂房的开挖过程。

4 地下厂房开挖施工的有限元模拟

地下厂房的开挖模拟在力学上是一个应力释放和回弹变形的过程。随着厂房的开挖，打破了原有的应力平衡，实现了应力的释放，目前应用最广的应力释放方法主要有“反转应力释放法”和“地应力自动释放法”[20]。反转应力释放法是把开挖边界上的初始应力反向后转换成等价的“释放载荷”施加在开挖边界上，并且在不考虑初始地应力的情况下进行有限元分析。具体的实现步骤如下。

根据前一开挖步的应力状态，从属于未开挖围岩边界节点上提取出节点力：

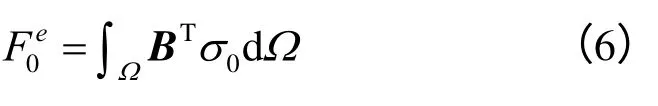
杀死开挖体的单元后在开挖边界处施加释放节点载荷：

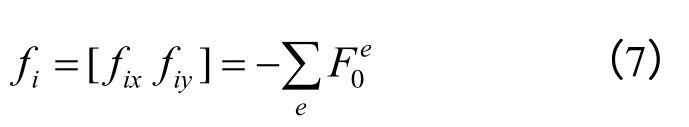
式中： fi为作用在开挖边界上第i 个节点的释放载荷； fix、 fiy分别为节点释放荷载的水平分量和垂直分量。

应力反转释放法所求得的位移场就是符合工程实际的位移场，所求得的应力场则需要叠加初始应力场。

地应力自动释放法通过应力的2次平衡实现应力的释放。岩体被开挖后，开挖边界上各点的应力平衡状态被打破，应力重分布并达到平衡，围岩产生变形。通过这种方法计算出开挖后围岩的应力场和位移场比较符合实际情况，并且操作简单，连续性好，计算结果和应力反转释放法非常接近，故而在地下工程的开挖模拟中被广泛的应用。本文就通过这种方法进行了地下厂房开挖过程的数值模拟，得到了各观测点处（CBX-1-3～CBX-5-4）的位移预测值，并与实际观测值进行对比，如图4所示。图4(a)表明，相对于围岩内12 m处，地下厂房右侧拱肩的变形方向指向洞室外。预测位移和观测位移结果一致，两者之间的相关系数为0.933；图4(b)表明，相对于围岩内25 m处，地下厂房右侧拱肩的变形方向与CBX-1-3一致。预测位移与观测位移曲线之间的相关系数为0.814；图4(c)表明，相对于围岩内12 m处，地下厂房左侧拱肩的变形方向指向洞室内。预测位移曲线和观测位移曲线之间的相关系数为0.786；图4(d)表明，相对于围岩内25 m处，地下厂房左侧拱肩的变形方向指向洞室内，预测位移曲线与观测位移曲线之间的相关系数0.847；图4(e)表明，相对于围岩内1.5 m，地下厂房左侧边墙的变形方向指向洞室内，预测位移曲线与观测位移曲线之间的相关系数为0.511；图4(f)表明，相对于围岩内5 m处，地下厂房左侧边墙的变形方向指向洞室内，预测位移曲线与观测位移曲线之间的相关系数为0.744；图4(g)表明，相对于围岩内12 m处，地下厂房左侧边墙的变形方向指向洞室内，预测位移曲线与观测位移曲线之间的相关系数为0.874。图4(h)表明，相对于围岩内25 m处，地下厂房左侧边墙的变形方向指向洞室内，预测位移曲线与观测位移曲线之间的相关系数为0.972。

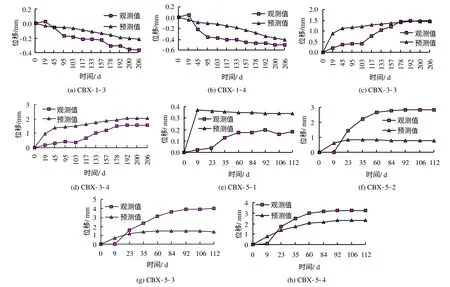
图4 开挖过程中不同位移计的观测值和预测值Fig.4 Comparison of observed and forecasted deformations in excavation process for CBX-1-4

由图4还可以看出，后续开挖步对于预测位移影响不大，预测位移曲线较平滑，与观测位移结果基本一致。这种参数反演的方法比较适用于构造应力随深度线性分布的地应力场。

5 结语

采用响应面分析方法，建立了未知的岩体力学参数同地下厂房开挖变形之间的关系。通过有限元正演分析确定了这种关系，并利用拟牛顿法进行了优化求解，反演出了未知的岩体力学参数。拟牛顿法对于初始估计值较敏感，相比遗传算法，反演结果可能是局部最优解，但是通过多组初始估计值下的反演可以得到全局近似最优解。

通过位移观测值和预测值的对比可以发现两者基本一致，验证了这种方法的有效性。

在参数反演过程中，假定有限元模型两侧侧压力系数相同，而地应力分布的实际情况比较复杂。把有限元模型两侧的侧压力系数假设为不同数值时可能更符合真实情况，该模型有待于在以后的进一步研究中予以考虑。

[1]邓建辉，李焯芬，葛修润.BP网络和遗传算法在岩石边坡位移反分析中的应用[J].岩石力学与工程学报，2001，20(1):1－5.DENG Jian-hui，LEE C F，GE Xiu-run.Application of BP network and genetic algorithm to displacement back analysis of rock slopes[J].Chinese Journal of Rock Mechanics and Engineering，2001，20(1):1－5.

[2]易达，徐明毅，陈胜宏.遗传算法在岩体初始应力场反演中的应用[J].岩石力学与工程学报，2001，20(增刊2):1618－1622.YI Da，XU Ming-yi，CHEN Sheng-hong.The application of genetic algorithm to the back analysis of initial stress field of rock masses[J].Chinese Journal of Rock Mechanics and Engineering，2001，20(Supp.2):1618－1622.

[3]王芝银，杨志法.岩石力学位移反演分析回顾及进展[J].力学进展，1998，28(4):488－498.WANG Zhi-yin，YANG Zhi-fa.A review on inverse analysis of displacements in rock mechanics[J].Advance in Mechanics，1998，28(4):488－498.

[4]JAVADI A A，FARMANI R，TOROPOV V V，et al.Identification of parameters for air permeability of shotcrete tunnel lining using a genetic algorithm[J].Computers and Geotechnics，1999，25(1):1－24.

[5]高玮，郑颖人.采用快速遗传算法进行岩土工程反分析[J].岩土工程学报，2001，23(1):120－122.GAO Wei，ZHENG Ying-ren.Back analysis in geotechnical engineering based on fast-convergent genetic algorithm[J].Chinese Journal of Geotechnical Engineering，2001，23(1):120－122.

[6]MONMARCHE N，VENTURINI G，SLIMANE M.On how Pachycondyla apicalis ants suggest a new search algorithm[J].Future Generation Computer Systems，2000，16(8):937－946.

[7]李宁，尹森菁.边坡安全监测的仿真反分析[J].岩石力学与工程学报，1996，15(1):9－18.LI Ning，YIN Sen-qing.Back analysis of the safety factor for slop[J].Chinese Journal of Rock Mechanics and Engineering，1996，15(1):9－18.

[8]李宁，辛有良.华盛顿地铁福特—图特站的仿真反分析[J].西安理工大学学报，1996，12(4):324－329.LI Ning，XIN You-liang.The simulation back analysis of Washington subway’s Fort-Totten station[J].Journal of Xi’an University of Technology，1996，12(4):324－329.

[9]叶飞，丁文其，朱合华，等.公路隧道现场监控量测及信息反馈[J].长安大学学报(自然科学版)，2007，27(5):79－83.YE Fei，DING Wen-qi，ZHU He-hua，et al.Site monitoring and information feedback of highway tunnel[J].Journal of Chang’an University(Natural Science Edition)，2007，27(5):79－83.

[10]朱合华，刘学增.基于遗传算法的混合优化反分析及比较研究[J].岩石力学与工程学报，2003，22(2):197－202.ZHU He-hua，LIU Xue-zeng.Comparison study of mixed optimal methods based on genetic algorithm in back analysis[J].Chinese Journal of Rock Mechanics and Engineering，2003，22(2):197－202.

[11]冯夏庭，张治强.位移反分析的进化神经网络方法研究[J].岩石力学与工程学报，1999，18(5):529－533.FENG Xia-ting，ZHANG Zhi-zhong.Study on genetic-neural network method of displacement back analysis[J].Chinese Journal of Rock Mechanics and Engineering，1999，18(5):529－533.

[12]高玮.基于粒子群优化的岩土工程反分析研究[J].岩土力学，2006，27(5):795－798.GAO Wei.Back analysis algorithm in geotechnical engineering based on particle swarm optimization[J].Rock and Soil Mechanics，2006，27(5):795－798.

[13]高玮，冯夏庭.地下工程围岩参数反演的仿生算法及其工程应用研究[J].岩石力学与工程学报，2002，21(增刊2):2521－2526.GAO Wei，FENG Xia-ting.Bionics algorithm for parameter inversion in underground engineering and engineering application[J].Chinese Journal of Rock Mechanics and Engineering，2002，21(Supp.2):2521－2526.

[14]KARAKUS M，FOWELL R J.Effects of different tunnel face advance excavation on the settlement by FEM[J].Tunnelling and Underground Space Technology，2003，18(5):513－523.

[15]陈帅宇，周维垣，杨强，等.三维快速拉格朗日法进行水布垭地下厂房的稳定分析[J].岩石力学与工程学报，2003，22(7):1047－1053.CHEN Shuai-yu，ZHOU Wei-yuan，YANG Qiang，et al.Analysis of stability of surrounding rocks of Shuibuya underground plant by three–dimensional fast Lagrangian method[J].Chinese Journal of Rock Mechanics and Engineering，2003，22(7):1047－1053.

[16]赖跃强，姜小兰.彭水枢纽地下洞室开挖应力及稳定试验研究[J].长江科学院院报，1998，15(1):23－25.LAI Yue-qiang，JIANG Xiao-lan.Experimental study on stress and stability of Pengshui Project’s underground grottos during excavation[J].Journal of Yangtze River Scientific Research Institute，1998，15(1):23－25.

[17]TEZUKA M，SEOKA T.Latest technology of underground rock cavern excavation in Japan[J].Tunneling and Underground Space Technology，2003，18(2－3):127－144.

[18]徐平，陈代华.水布垭枢纽地下厂房围岩稳定三维弹塑性分析[J].长江科学院院报，1999，16(1):48－51.XU Ping，CHEN Dai-hua.Three dimensional elastoplastic analysis of stability of surrounding rock of Shuibuya underground plant[J].Journal of Yangtze River Scientific Research Institute，1999，16(1):48－51.

[19]李宁，段庆伟.乌江思林水电站地下厂房洞群的数值仿真分析[J].水力发电学报，1996，17(1):43－50.LI Ning，DUAN Qing-wei.Numerical emulation analysis for a underground structure of the Silin hydropower station on the Wujiang river[J].Journal of Hydroelectric Engineering，1996，17(1):43－50.

[20]王文正，夏永旭，胡庆安.公路隧道施工过程的数值模拟及ANSYS实现[J].西部交通科技，2007，2(4):1－4.WANG Wen-zheng，XIA Yong-xu，HU Qing-an.Realization of numerical simulation and ANSYS during highway tunnel construction[J].Western China Communication Science&Technology，2007，2(4):1－4.