坐标转换中公共点粗差定位与降低粗差点影响方法研究*

吴祖海 罗伟钊 李 军

(中南大学土木工程学院，长沙 410004)

1 引言

GPS 定位使用的是WGS84 坐标系，我国工程领域常用的坐标系有北京54 坐标系、西安80 坐标系、CGCS2000 坐标系和地方独立坐标系。故使用GPS技术建立控制网将遇到坐标转换的问题。布尔莎七参数模型是三维空间直角坐标转换常用的方法。运用布尔莎模型求解七参数时，没有考虑公共点本身存在的误差。若起算公共点存在粗差，将造成模型扭曲，出现错误的转换结果［1］。因此坐标转换首先要剔除起算数据中的粗差或者降低粗差的影响。

GPS 定位技术具有精度高稳定性好的优点，如果外业操作按相关测量规范进行，可以认为整个网中WGS84 坐标的精度较高［2］。而公共点中的地方坐标，由于坐标点的建立年代不一，来源不一，或者标石移动，精度可能参差不齐。诸如以上情形，起算公共点中可能混有粗差点。对于含有粗差的数据处理一般分为两种方法:将粗差归入函数模型［3］或将粗差归入随机模型［4，5］。选择适当的权函数，消除或者削弱粗差对参数估计的影响。这一类方法的困难在于合理权函数的选择，抗差的严密精度有待进一步研究［6］。

上述方法主要通过经最小二乘计算得到的改正数V 来判定粗差。最小二乘法具有平均分配误差的能力，会导致粗差在平差改正数中的反映小于原始粗差量，并且第i 个观测值的粗差不仅仅作用于第i 个改正数V，还影响其他的改正数［3］。直观表现就是含有粗差的公共点的改正数不一定会大，此时会造成误判粗差的情况。本文提出一种新方法，利用最小二乘平差后的方差构建统计量，克服了常规粗差定位中使用改正数V 容易掩盖粗差的缺点，实现了在布尔莎七参数计算过程中的粗差定位和剔除。鉴于实际工程中用于坐标转换的起算公共点较少，在公共点不适宜直接剔除的情况下，结合假设检验与降权迭代计算两种方法，定位出粗差点并通过降权来削弱其影响，得到准确的坐标转换参数。

2 方差比值检验法

2.1 坐标转换数学模型

设A 为目标坐标系，B 为源坐标系。考虑到三个欧拉角都非常小，因此布尔莎模型可简化为［7］:

误差方程写成矩阵形式为:

将L 视作观测向量。则转换参数的估值为:

由于各点的坐标可以视作是同精度独立观测值，因此P=I。然后可求得单位权中误差为:

式中n 为公共点的个数。

2.2 方差比值检验法的原理

构建统计量Fi算法流程如下:

1)利用所有公共点，构建误差方程

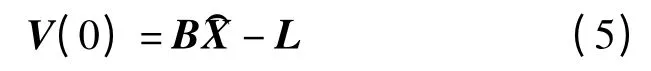
2)此时不知道哪个已知点中的坐标是含有粗差的，逐个删除公共点对进行检验。对第i 对点进行检验时，将第i 对公共点删除，即第i 对点不参与构成误差方程。得到不含第i 个点平差的中误差

3)逐个去掉公共点对完成一轮计算，得到剔除了第i 对公共点的。如果母体含有粗差，该粗差恰好在第i 对公共点上，则应有。进行如下统计检验:

针对每一对公共点，构建统计量［7］

Fi服从F 分布［8］，即有:

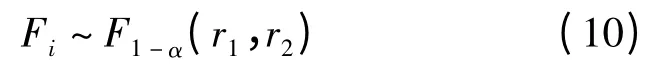
式中α 为显著性水平，r1、r2为自由度，若参与平差的公共点对数为n，则相应自由度为r=3n－7。

运用上述方法时，有两个值得注意的地方:

1)在多个粗差同时存在的情况下，为防止各个粗差相互干扰，特别是大粗差掩盖小粗差，每轮检验只剔除一个粗差点［9］，即只对最小的点进行检验。剔除一个粗差点后，再开始第二轮平差计算，剔除下一个粗差点，直至所有粗差被剔除。

2)显著性水平α 的选取问题。如果α 偏小，则发现粗差的能力偏低，会出现放过粗差的情况，犯统计假设的第二类错误。如果α 偏大，则容易把不是粗差的点识别为粗差，犯统计假设的第一类错误。对于该检验方法，设置的显著性水平应该偏大。一是如果公共点含有粗差时，则必然有会小于所有点参与平差的，因此会是单侧检验;二是当公共点不含有粗差时，删除某个点对方差的影响很小，此时的统计量应分布于较小的概率区间［9］。因此可以适当增大显著性水平α 以便发现所有粗差点。

3 降权迭代计算法

利用上述方法进行坐标转换粗差剔除时有时会带来一个问题，即实际工作中建立GPS 网时，公共点的对数往往是比较少的，而布尔莎模型七参数转换要求公共点个数至少为三个。如果将探测出来的粗差点全部剔除，可能造成无法转换的情形，或者出现公共点全部集中在网的一侧或一角，这对整个网形的精度是不利的［8］。此时考虑一种将粗差点降权处理的方法，该方法与稳健估计类似，重新构建权函数来减小粗差点在坐标转换中的影响，而不是将粗差点直接剔除。

这种方法的思路是先利用方差比值检验法探测出粗差，然后根据权与方差成反比的定义，给予这些观测值一个相应较小的权进行下步平差迭代计算，逐步减小粗差值的影响。为达到上述目的，设置两个显著性水平，α1较大，α2略小，α2设置为剔除粗差的限值，α1与α2之间则进行降权处理，α1以下则不作处理。根据多次试验，α2取为0.05，α1取为0.35。建立权函数如下:

式中上标v表示的是迭代次数。

转换参数的估值公式化为:

在降权处理法中，粗差探测相当于第一次迭代计算。第一次计算时，所有公共点对是等权计算，由于粗差的影响，得到的结果是有偏估计。然后在各次迭代过程中不断变化公共点的权值，含有粗差的公共点的权逐步减小，从而降低这些点在平差中的贡献度，使有偏估计逐步接近无偏估计。

为减少计算量，对第一次平差计算后得到的统计量进行筛选，取Fi大于1 所对应的坐标点进行检验。将这部分公共点看做疑似粗差点，迭代过程中仅对这部分点进行降权处理。

4 算例

4.1 用方差比值检验法剔除粗差

现取一GPS 网数据进行分析。该网共8 个公共点(表1)。起初，公共点的精度都比较高，求得的坐标转换七参数及单位权中误差见表3。然后在第三个点和第六个点的x，y，z 坐标上加入3 cm 的误差，第八个点x，y，z 坐标上上加入5 cm 的粗差，加入粗差后的坐标见表2。利用最小二乘普通坐标转换方法求得的七参数见表3。

表1 不含粗差的公共点坐标(单位:m)Tab.1 Common coordinates without gross errors(unit:m)

表2 加入粗差后公共点在54 坐标系中的坐标(单位:m)Tab.2 Coordinates with gross errors in BJZ54(unit:m)

利用方差比值检验法进行粗差探测，求得的统计量Fi如表4。

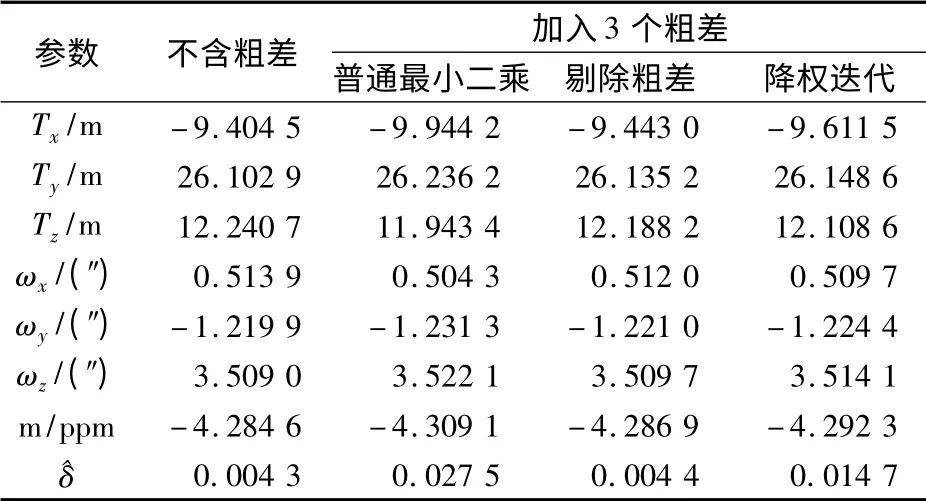
表3 坐标转换参数计算值Tab.3 Calculated coordinates transformation parameters

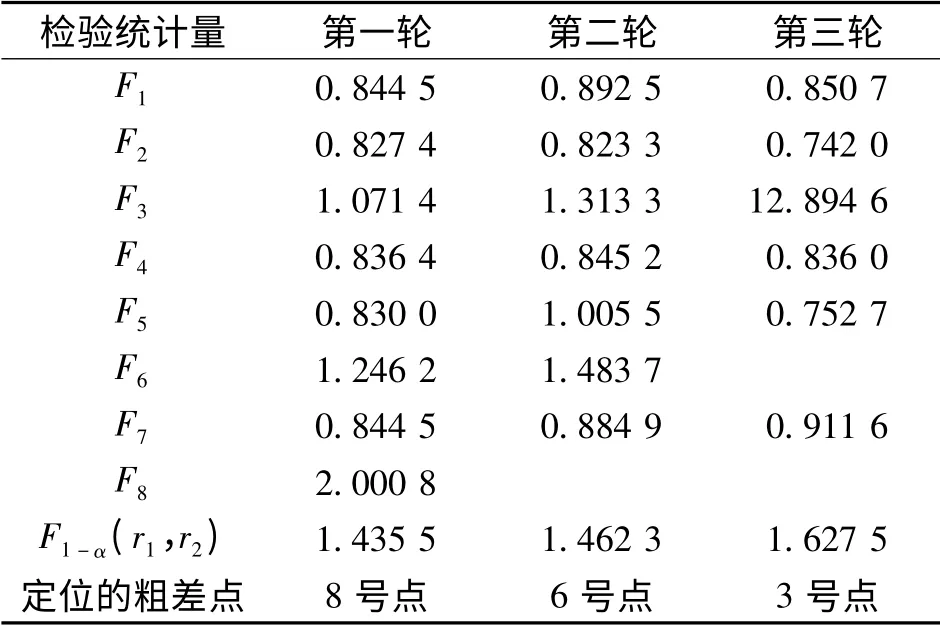
表4 方差比值检验法的统计量Tab.4 Stastics of variance-ratio method

例中，取显著性水平α 为0.25，通过三轮检验，第一轮探测时F0.75(17，14)=1.435 5，可以探测出8 号点为粗差点;第二轮探测时F0.75(14，11)=1.462 3，可以探测出6 号点为粗差点;第三轮探测时F0.75(11，8)=1.627 5，探测出3 号点为粗差。剔除这三个点后，重新计算坐标转换参数及单位权中误差见表3，此时计算出的坐标转换参数跟不含粗差时基本相同，中误差也很接近。可见运用该方法能识别公共点中的粗差，剔除粗差点后，坐标转换的精度得到显著提高。

4.2 降权迭代计算降低粗差影响

仍然用表1 和表2 中的数据。为便于发现粗差，设置显著性水平α2为0.05，α1为0.35，由方差比值定权并进行迭代计算。

首次平差计算得到的统计量Fi如表4 第一列所示。大于1 的统计量对应的点有3 号点，6 号点和8 号点，因此只对这3 个点进行检验并作降权处理。其中F0.65(17，14)=1.232 9，F0.95(17，14)=2.428 2 迭代7 次后，达到终止条件。各次迭代得到的权值如表5。

表5 迭代计算得到的权值Tab.5 Weights calculated by iteration

可见通过迭代，含有粗差的公共点的权值不断降低，其他点的权值仍为1，权值也指出了粗差点的位置。终止迭代时得到的转换参数和中误差见表3。

通过对比，降权迭代计算后得到的七参数与不含粗差时较为接近，中误差也有显著减小，七参数的精度有了提高，说明在不直接剔除粗差公共点的情况下，该方法明显优于普通最小二乘计算方法。

5 结论

1)本文提出的方差比值检验法，原理简单，公共点存在多维粗差时可以对粗差进行准确定位，用以提高坐标转换的精度;

2)在公共点对数较少的情况下，可以利用降权处理方法，将假设检验与降权迭代计算结合起来，降低粗差在坐标转换过程中的贡献度，使有偏估计逐步接近无偏估计，在保证坐标转换顺利进行的前提下，削弱粗差点的影响;

3)由于每次计算检验统计量都需要重新平差计算，计算工作量较大。但坐标转换的公共点数目往往不会很多，借助于计算机编程，该方法是完全可行的。在其他平差计算过程中，该方法的应用值得探讨。

1 陈义，陆珏.以三维坐标转换为例解算稳健总体最小二乘方法［J］.测绘学报，2012，(5):715－722.(ChenYi and Lu Jue.Performing 3D similarity transformation by robust total least squares［J］.Acta Geodaeticaet Cartographica Sinica，2012，(5):715－722)

2 郭英起，黄声享，曹先革.基于稳健估计的高精度坐标转换参数解算方法［J］.测绘工程，2008，(6):6－8.(Guo Yingqi，Huang Shengxiang and Cao Xiange.A method for calculating parameters with high accuracy in coordinate transformation based on robust estimation［J］.Engineering of Surveying And Mapping，2008，(6):6－8)

3 於宗俦，李明峰.多维粗差的同时定位与定值［J］.武汉测绘科技大学学报，1996，(4):17－23.(Yu Zongchou and Li Mingfeng.Simultaneous position and evaluation with multidimensional gross errors［J］.Journal of Wuhan Technical University of Surveing and Mapping，1996，(4):17－23)

4 周江文.经典误差理论与抗差估计［J］.测绘学报，1989，(02):115－120.(Zhou Jiangwen.Classical theory of errors and robust estimation［J］.Acta Geodaeticaet Cartographica Sinica，1989，(02):115－120)

5 郭英起，等.基于空间直角坐标系的高精度坐标转换方法研究［J］.大地测量与地球动力学，2012，(3):125－128.(Guo Yingqi，et al.Study on coordinate transformation method with high accuarcy based on space rectangular coordinates system［J］.Journal of Geodesy and Geodynamics，2012，(3):125－128)

6 李德仁，袁修孝.误差处理与可靠性理论［M］.武汉:武汉大学出版社，2002.(Li Deren and Yuan Xiuxiao.Error processing and reliability theory［M］.Wuhan:Wuhan University Press，2002)

7 武汉大学测绘学院测量平差科学组.误差理论与测量平差基础［M］.武汉:武汉大学出版社，2003.(Surwey Adjustment Discipline Unit of Surveying and Mapping College of Wuhan University.Basis of error theory and adjustment［M］.Wuhan:Wuhan University Press，2003)

8 李金生.GPS 网基线解算质量控制及基准点可靠性检验［D］.东北大学，2008.(Li Jinsheng.Quality control of baseline solution and reliableexamination of datum points in GPS network［M］.Northeastern University，2008)

9 高北晨，杨腾峰.多维粗差的逐步剔除［J］.铁路航测，1997，(1):6－8.(Gao Beichen and Yang Tengfeng.Gradually eliminating of multimensional gross errors［J］.Railway Investigation and Surveying，1997，(1):6－8)

附件

根据抗差等价加权原理［4］，坐标转换误差方程为:

最小二乘估计准则为:

但最小二乘估计的抗差能力很差，于是采用抗差稳健估计，估计准则如下:

令

式(4)可化为:

记

则式(6)可化为

写成矩阵形式，为:

常规方法中多使用改正数v 定位粗差，但最小二乘法具有平均分配粗差能力，改正数V 容易掩盖粗差。因此利用最小二乘平差后的方差构建统计量，实现粗差定位和剔除。鉴于实际工程中用于坐标转换的起算公共点较少，在公共点不适宜直接剔除的情况下，结合假设检验与降权迭代计算两种方法，定位出粗差点并通过降权来削弱其影响，得到准确的坐标转换参数。

当采用方差比值检验法求取坐标转换参数时，论文利用假设检验原理，直接剔除粗差点。

当采用降权迭代计算方法时，构建新的权函数如下:

利用迭代最终的权矩阵，通过式(9)求取坐标转换参数，削弱粗差点的影响。