利用无整周单历元算法进行连续变形监测的试验分析*
2014-02-13白征东蒋国辉
白征东 任 常 蒋国辉
1)清华大学土木工程系地球空间信息研究所,北京 100084
2)麦格集团,北京100043
1 引言
GPS 技术已经广泛应用于变形监测各个领域,并且提出了适用于小变形监测的无整周单历元算法[1-3],这种算法的优点在于不需要进行周跳的探测和修复,只需要一个历元的观测数据就可以进行变形信息的解算。本文在分析这种算法特点的基础上,提出利用高采样率接收机和无整周单历元算法进行连续变形监测,并通过试验验证了这种方法的可行性。
2 无整周单历元算法的数学模型
如图1 所示,A 为基准点,C 为变形监测点,i、j为卫星,在A 点和C 点建立载波观测方程为[4-7]:
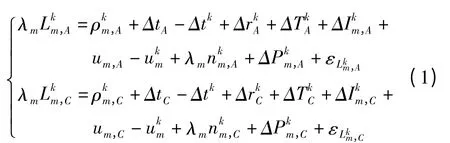
式中λm为波长,为载波观测值,为m 频率上卫星天线相位中心在信号发射时刻的位置与接收机天线相位中心在信号接收时刻的位置之间的几何距离,Δtk为接收机钟差,Δtk为卫星钟差,为相对论效应,为对流层延迟,为电离层延迟,um、为接收机和卫星未标定的相位延迟(UPD),为整周模糊度,为天线相位绕转,为观测噪声,k=i,j。

图1 原理示意图Fig.1 Diagram of principle
若A 点和C 点之间距离很短,组成双差观测方程后各项误差得到很好的消除,忽略观测噪声后有
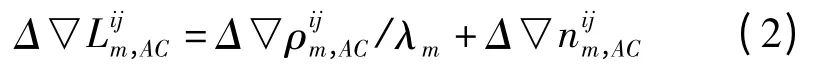
其中

A 点为基准点,利用首期观测可以得到其精确坐标,C 点变形点,其坐标会变化,只能利用首期观测得到其近似坐标点B,记B 点坐标为[xB,yB,zB],B 点和C 点间的位移即为待求变形量,记为

记A 点坐标为[xA,yA,zA],卫星i 坐标为[xi,yi,zi],卫星j 坐标为[xj,yj,zj],有

当δu 很小时,式(4)在[Δx,Δy,Δz]=[0,0,0]处进行泰勒展开,忽略高阶项后得

其中

当变形量δu 很小时,有
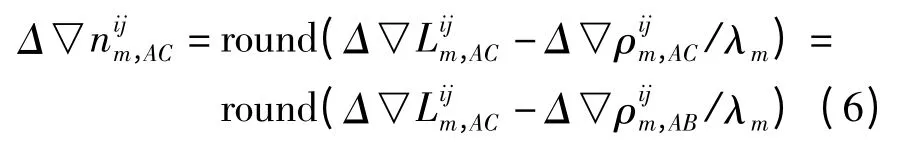
其中round()为四舍五入取整函数。
将式(5)、(6)代入式(2)后可得
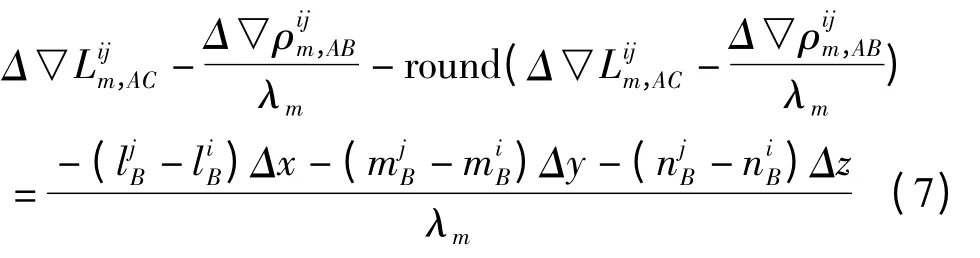
改成误差方程形式后有
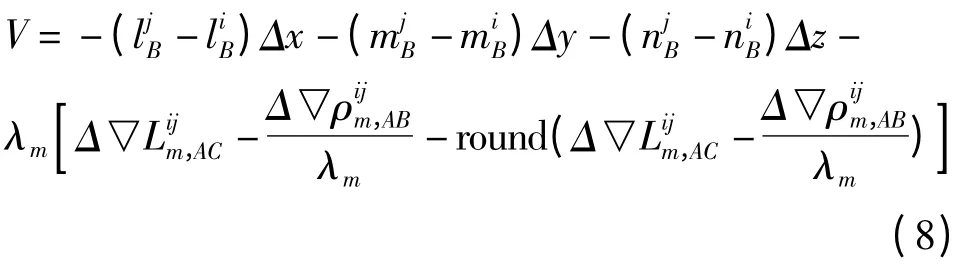
式(8)即为无整周单历元算法解算变形量的误差方程,待求参数为[Δx,Δy,Δz],由于采用了双差观测方程,因此当共视卫星数大于等于4 颗时便可以解算变形。
3 连续变形监测方法
由推导可以看出无整周单历元算法在解算过程中必须要知道监测点的近似坐标,笔者对监测点近似坐标的精度是否会影响变形信息的解算进行了验算。利用已有的短基线数据,其参考站与流动站的坐标精确已知,将流动站作为变形监测的监测站,利用无整周单历元算法计算某历元监测点相对于已知坐标的变形量为[2.7,0.2,1.9]mm(此变形量应为[0,0,0]),然后对监测点初始坐标增加半径为20 mm 的球面坐标改变量,计算根据不同初始坐标计算出的相对于已知坐标的变形量如图2 所示。
图2 中的颜色代表计算出的坐标相对于已知坐标的距离,可以看出,当初始坐标在小范围内变动时,根据不同初始坐标计算出的变形量与根据精确坐标计算出的变形量一致,均为

图2 不同初始坐标计算出的变形量Fig.2 Deformation calculated with different initial coordinates
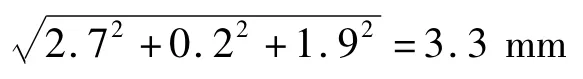
记初始坐标为U,初始坐标变动量为ε,ΔuU表示利用无整周单历元算法计算出的相对于坐标U的变形量,如果基线较短并且初始坐标变动量ε 较小时有ΔuU=ΔuU+ε+(U+ε)-U 即

在连续变形监测中,在历元1 可以计算出相对于坐标U 的变形量δu1,在历元2 由于监测点与坐标U 可能相差较大,无法将U 作为初始坐标进行变形解算,但由于位移具有连续性,历元2 与历元1 间的变形可能会相对小,因此可以在历元2 利用无整周单历元算法计算出相对于初始坐标U +δu1的变形量δu2,由式(9)可知历元2 相对于坐标U 的变形量为

并且历元1 变形的解算误差不会对历元2 的变形解算带来误差,因为初始坐标在准确坐标小范围内变化时并不影响变形解算。
利用式(10)进行连续变形解算时需要保证每个历元的变形较小,在实际中往往无法控制变形大小,但可以通过高采样率的接收机缩小相邻历元的时间间隔减小每个历元的位移,从而通过实时更新初始坐标就可以利用无整周单历元算法进行连续变形解算。
4 试验分析
试验于2013年4月在清华大学土木工程系地球空间信息研究所楼顶进行。在楼顶设置一基准点和一监测点,基线长度8 m。采用两台Trimble 双频接收机进行观测数据采集,接收机采样率设置为10 Hz。
试验1:将监测点接收机安置在一可做往复运动的平台上,首先静止观测5 分钟左右,然后让监测点接收机沿东西方向做振幅约10 cm 的往复运动,利用无整周单历元算法进行连续变形解算,结果如图3 ~5 所示。
从图3 ~5 可以看出,利用该方法准确地解算出了东西方向的往复运动,南北方向和高程方向的变形均比较稳定,单历元解算误差均在1 cm 以内。值得说明的是,如果不根据上一个历元更新初始坐标,在振幅较大处由于不满足相对于初始坐标的小变形要求,利用未改进的无整周单历元算法就不能解算正确的变形信息。
试验2:将监测点接收机仍安置在该平台上,开始静止观测6 分钟左右,然后将监测接收机沿东西方向移动,最大移动量约0.8 m,利用该方法解算出的东西方向变形如图6 所示。
从图6 可以看出,利用这种方法可以很好地解算出连续的大变形。
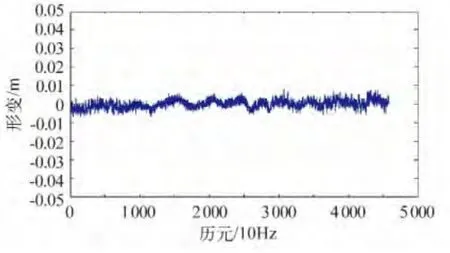
图3 N 方向变形Fig.3 Deformation of N direction
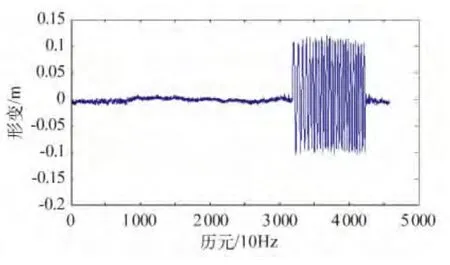
图4 E 方向变形Fig.4 Deformation of E direction
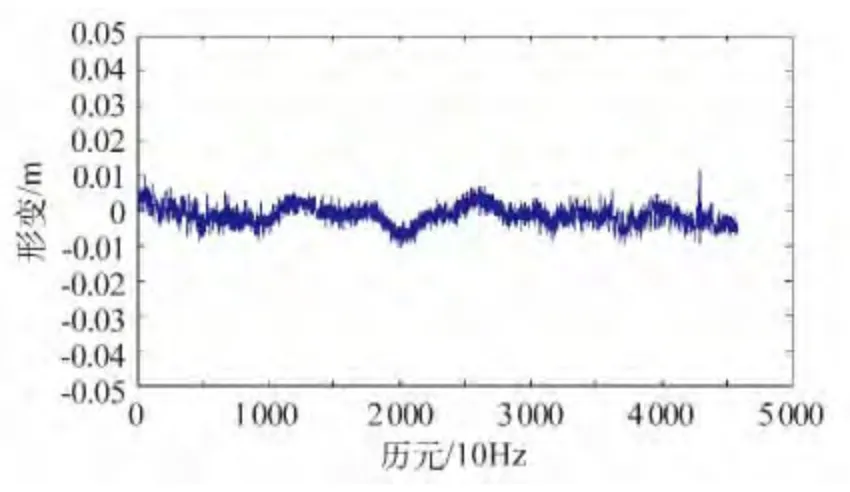
图5 U 方向变形Fig.5 Deformation of U direction
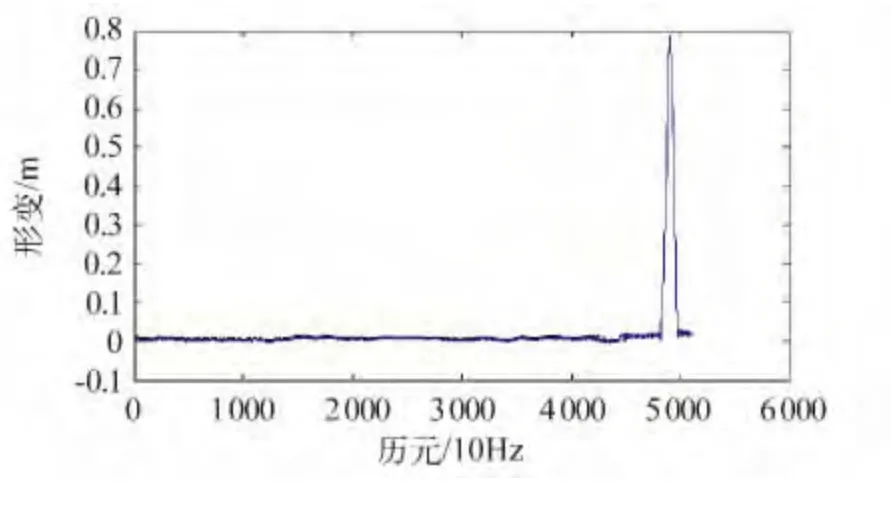
图6 E 方向连续大变形Fig.6 Continuous large deformation of E direction
5 总结
根据适用于小变形监测的无整周单历元算法在监测点初始坐标有小扰动时并不影响变形信息的解算这一特点,提出了可以利用高采样率接收机进行数据采集,实时利用前一个历元解算出的变形更新下一个历元的初始坐标,从而利用无整周单历元算法进行连续变形监测,试验验证了这种方法是可行的。
1 张小红,李征航,徐绍铨.高精度GPS 形变监测的新方法及模型研究[J].武汉大学学报(信息科学版),2001,(5):451-454.(Zhang Xiaohong,Li Zhenghang and Xu Shaoquan.Study on the method and the model for high accuracy deformation monitor with GPS[J].Geomatics and Information Science of Wuhan University,2001(05):451-454)
2 李征航,张小红,朱智勤.利用GPS 进行高精度变形监测的新模型[J].测绘学报,2002,31(3):206-210.(Li Zhenghang,Zhang Xiaohong and Zhu Zhiqin.A new model of high accuracy deformation monitoring with GPS[J].Acta Geodaetica et Cartographica Sinica,2002,31(3):206-210)
3 楼益栋,李征航,张小红.无模糊度和整周跳变问题的短基线解算方法研究[J].武汉大学学报(信息科学版),2005(11):995-997.(Lou Yidong,Li Zhenghang and Zhang Xiaohong.A method of short baseline solution without cycle slip detection and ambiguity resolution[J].Geomatics and Information Science of Wuhan University,2005,(11):995-997)
4 李厚芝.单基准线向量解算法在GPS 变形监测中的应用[J].测绘科学,2007(06):137-139.(Li Houzhi.Application of single baseline vector solution to GPS deformation monitoring[J].?Science of Surveying and Mapping,2007,(6):137-139)
5 李波,葛永慧.单历元GPS 变形监测数据处理与系统研制[J].河南理工大学学报(自然科学版),2007(02):169-170.(Li Bo and Ge Yonghui.Study on data processing method and system in GPS deformation monitoring[J].Journal of Henan Polytechnic University(Natural Science),2007,(2):169-170)
6 王新洲,花向红,邱蕾.GPS 变形监测中整周模糊度解算的新方法[J].武汉大学学报(信息科学版),2007,(1):24-26.(Wang Xinzhou,Hua Xianghong and Qiu Lei.A new method for integer ambiguity resolution in GPS deformation monitoring[J].Geomatics and Information Science of Wuhan University,2007,(1):24-26)
7 李征航,张小红.卫星导航定位新技术及高精度数据处理方法[M].武汉:武汉大学出版社,2009.(Li Zhenghang and Zhang Xiaohong.New techniques and precise data processing methods of satellite navgation and positioning[M].Wuhan:Wuhan University Press,2009)
