基于全球IGS数据分网确定GPS卫星轨道*

潭冰峰 袁运斌 刘 腾 王宁波

1)中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室，武汉 430077

2)中国科学院大学，北京100049

1 引言

GNSS 导航星座精密定轨技术是保证导航系统运行最关键的核心技术，GNSS 轨道精度直接影响影用户定位、测速及授时的精度［1－5］。目前，国际上进行导航星座精密定轨时大多采用动力学定轨方法，该方法受到卫星动力学模型误差以及数据处理策略等因素的综合影响。有效地综合考虑各类力学模型并且合理地选取定轨处理策略与流程是实现导航星座精密定轨的关键。另外，随着IGS 全球跟踪站的迅速增加，如何合理地对全球IGS 跟踪网进行分网，提高计算效率也是导航卫星精密定轨中需要考虑的重点问题［1，6，7］。

本文研制了一套GPS 导航星座精密定轨软件，并利用全球200 个IGS 跟踪站2012年年积日001—031 一个月的观测数据，实现了GPS 导航星座精密定轨。并选取IGS 最终轨道产品作为参考，评定了基于本软件的定轨精度［8－12］。

2 方法与处理流程

2.1 数据质量控制策略

完善的数据质量控制体系是保障高精度GPS导航星座定轨的重要前提。在进行定轨处理时，采用双差无电离层组合的相位观测数据，伪距观测数据仅用于接收机时间同步。相位数据预处理采用三差方式逐基线进行，一般情况下，周跳可以得到很好的修复。如果周跳没有被合理修复，相应的观测数据将被剔除，新的模糊度参数也将被设置。程序中也采用了通过加权验后残差分析的方法进行粗差检测与剔除，即:在进行迭代计算时，对双差无电离层组合的相位观测值，设定一定阈值(本文取为4 mm)，超限的观测值将会被剔除。

2.2 力学模型及处理策略

基于卫星轨道特点以及长时间数据处理经验，选取合理的力学模型及处理策略，是GPS 导航星座精密定轨的核心问题［13－15］。表1 给出了改进得到的适用于GPS 导航星座精密定轨的观测模型和力学模型。

2.3 双差模糊度固定策略

定轨处理过程中，先进行单天解算，单天解算分为两个步骤:模糊度浮点解和模糊度固定解。在进行双差模糊度固定时，根据基线长度选取了不同的策略:

1)对于2 000 千米以下的基线，采用QIF(Quasi-Ionosphere-Free approach)方法固定双差模糊度;

2)对于2 000 千米以上的基线，采用M-W(Melbourne-Wuebbena)线性组合与L3 线性组合结合的方式，固定双差模糊度。

2.4 分网定轨策略及流程

为了有效地提高计算效率，在单天模糊度浮点解和模糊度固定解进行参数估计之前，进行了分网处理，将全球200 个IGS 跟踪站划分为4 个子网，分别作参数估计形成法方程，然后通过法方程叠加的方式，生成单天模糊度浮点解和模糊度固定解。针对此，本文研究了一种优化的分网方法:根据测站的几何分布将全球IGS 观测网分为3 个子网(欧洲区域，美洲区域，亚洲、澳大利亚、非洲和大洋洲区域)，将3 个子网以外的观测站设为第4 个子网。4个子网的分布如图1 所示。其中，蓝色倒三角表示欧洲区域观测站(编号1)，绿色菱形表示美洲区域观测站(编号2)，紫色正方形表示亚洲、澳大利亚、非洲和大洋洲区域观测站(编号3)，红色圆圈表示前3 个子网以外的观测站(编号4)。

表1 观测模型和力学模型Tab.1 Observation models and dynamic models of GPS navigation constellation POD

编号1 ～3 为全球分布比较密集的三个大区域，三个网内作参数估计的时候，严格考虑网内基线的数学相关性。编号为4 的观测站，数量不多，大约只占10%，且形成基线时比较长，但是这些少量的站，可以起到连接其他三个子网以增强整网几何结构的作用。

基于Linux 的并行计算的处理方式，可调用多个CPU 同时对4 个子网进行参数估计形成法方程并存储，大大缩短了计算时间，最终通过4 个子网的法方程叠加，生成单天模糊度浮点解和模糊度固定解。

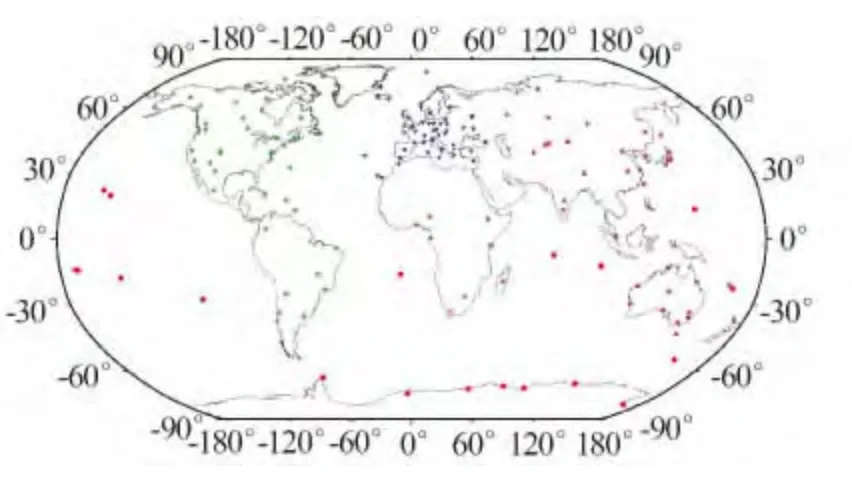
图1 全球IGS 跟踪站分网图Fig.1 Station clusters of global IGS stations

2.5 最终轨道生成流程

由于单天解受限于定轨弧段限制，观测数据有限，且相邻天轨道具有不连续性，软件中，基于单天模糊度固定解得到的法方程，将连续3 个单天的法方程进行叠加生成三天长弧段轨道，并在连接时段附加伪随机脉冲加速度，得到三天解。将连续7 个具有重叠弧段的三天解法方程进行叠加，生成周解结果(9天解，覆盖整个GPS 周，以及上一周最后一天和下一周开始第一天)，周解进行参数估计时，得到稳定的站坐标结果以及一周的地球自转参数ERP 结果。最终，将周解得到的站坐标和ERP 结果作为约束，重新进行最终三天解。

整个数据处理流程如图2 所示。当得到最终三天解之后，取中间一天轨道结果作为最终轨道，并与IGS 最终轨道产品进行比较，进行精度评定。

3 定轨结果分析

将基于本文中研究的定轨策略以及研制的GPS导航星座精密定轨软件，解算得到的GPS 导航星座2012年年积日001—031 一个月的最终轨道结果，与IGS 最终轨道产品互差，并统计径向、切向、法向及1D 向位置偏差的均方根(图3)。

由图3 可知，基于本文提出的定轨策略解算得到的GPS 导航星座精密定轨最终轨道，与IGS 最终轨道产品互差，在径向、切向、法向三个方向位置偏差的均方根分别为:0.70、1.60、1.04 cm，1D-均方根差为1.23 cm，而目前IGS 最终轨道产品标称精度为1D-均方根差2.5 cm，因此，计算结果与IGS 最终轨道产品精度基本相当。

通过对一个月的计算结果，与IGS 互差后进行统计，发现结果与IGS 最终轨道产品没有明显偏差，精度相当，一个月的计算结果稳定。径向位置偏差的均方根统计结果在1 cm 以内，切向在1 cm 左右，法向约1.5 cm，这也符合动力学定轨的一般特征，沿迹方向一些摄动力一般难以被很好地模型化。

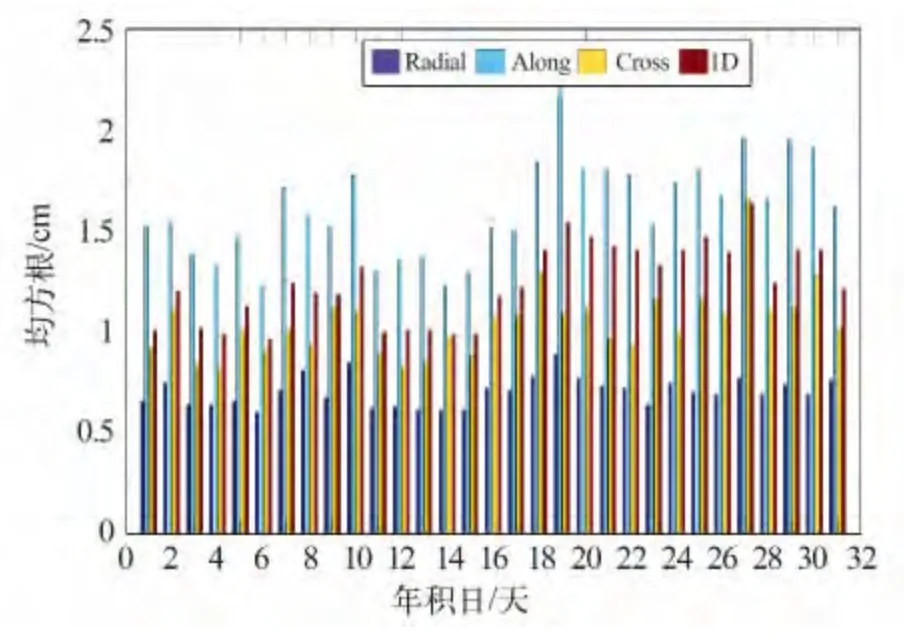
图3 定轨精度统计Fig.3 Flow chart of POD accuracy

另一方面，文中提出的定轨策略以及研制的GPS 导航星座精密定轨软件，通过对全球IGS 跟踪网进行分网定轨后，基于Linux 并行计算的技术，同时调用多个CPU 并行处理每个子网，然后通过法方程叠加实现基于全球IGS 跟踪网观测数据处理以实现GPS 导航星座精密定轨。图4 为30天分网与不分网的单天最终解计算时间统计图，计算平台同为Linux CentOS 64 位操作系统，CPU 单核主频为2.8GHz。由图4 可知，在硬件和操作系统完全相同的情况下，分网处理后大大提高了计算效率，使得原本需要8 小时的计算量，在2 小时内完成。

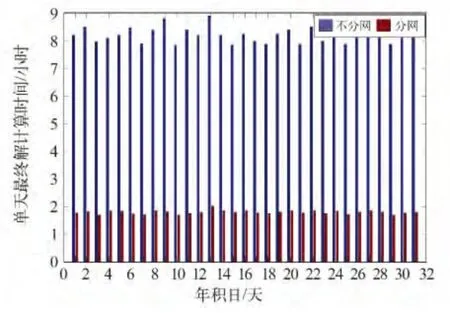
图4 单天最终解计算时间Fig.4 Computing time of final one-day resolution

4 结论

1)基于本文所提出的GPS 导航星座精密定轨策略以及研制的GPS 导航星座精密定轨软件，获得的GPS 导航星座精密轨道与IGS 最终轨道产品在径向、切向、法向、1D 方向位置偏差的均方根分别为:0.70、1.60、1.04、1.23 cm。计算结果稳定，不仅可满足相关领域的科研要求，而且对北斗卫星导航星座的精密定轨、星载GPS 低轨卫星精密定轨，也具有指导意义;

2)本文研制的定轨软件，合理地将全球IGS 跟踪站分为4 个子网，基于Linux 并行计算技术对各个子网进行定轨形成法方程，然后通过法方程叠加的方法实现基于全球IGS 站的GPS 导航星座精密定轨，大大提高了计算效率。

1 Hugentobler U and Beutler G I.Precise orbit determination and gravity field modelling:Strategies for precise orbit determination of low earth orbiters using the GPS［J］.Space Science Reviews，2003，108(1－2):17－26.

2 Lichten S M and Border J S.Strategies for high-precision global positioning system orbit determination［J］.Journal of Geophysical Research，1987，92(B12):12 712－12 751.

3 Steigenberger P，et al.Reprocessing of a global GPS network［J］.Journal of Geophysical Research.2006，111(B5):B5402.

4 楼益栋.导航卫星实时精密轨道与钟差确定［D］.武汉大学，2008.(Lou Yidong.Research on real-time precise GPS orbit and clock offset determination［D］.Wuhan University，2008)

5 赵齐乐.GPS 导航星座及低轨卫星的精密定轨理论和软件研究［D］.武汉大学，2004.(Zhao Qile.Research on precision orbit determination theory and software of both GPS naviagation constellation and LEO satellites［D］.Wuhan University，2004)

6 Boomkamp H and Dow J.High-performance algorithms for double difference data processing［A］.10 years IGS Workshop［C］.Berne:1－5 March，2004.

7 Herring T.Aspects of large station networks for GPS orbits and clocks［A］.10 years IGS Workshop［C］.Berne:1－5 March，2004.

8 Montenbruck O and Gill E.Satellite orbits:models，methods and applications［M］.Springer，2005.

9 Schutz B，Tapley B and Born G H.Statistical orbit determination［M］.Academic Press，2004.

10 彭碧波，夏炯煜，吴斌.利用LAGEOS 卫星激光测距资料解算海潮参数［A］.1990年中国地球物理学会第六届学术年会论文集［C］.1990.(Peng Bibo，Xia Jiongyu and Wu Bin.Calculating ocean loading parameters using SLR data of LAGEOS satellite［A］.Sixth Annual Conference Proceedings of Chinese Geophysical Society［C］.1990)

11 彭冬菊，吴斌.非差和单差LEO 星载GPS 精密定轨探讨［J］.科 学 通 报，2007，52(6):715－719.(Peng Dongju and Wu Bin.Study on precise orbit determination of low-earth satellites using satellite-borne non-difference and single-difference GPS data［J］.Chinese Science Bulletin，2007，52(6):715－719)

12 赵春梅，瞿锋.无准确初轨信息时星载GPS 低轨卫星定轨方法研究［J］.测绘科学，2006，31(3):23－24.(Zhao Chunmei and Qu Feng.Study on methods of lowearth satellites orbit determination based on GPS without accurate preliminary orbit position［J］.Science of Surveying and Mapping，2006，31(3):23－24)

13 杨旭海，等.GEO 卫星机动后的星历快速恢复方法［J］.中国科学:G 辑:物理学力学天文学，2008，38(12):1 759－1 765.(Yang Xuhai，et al.Methods of rapid recovering of GEO satellite ephemeris after maneuver［J］.Science China Physics，Mechanics ＆ Astronomy，2008，38(12):1 759－1 765)

14 欧吉坤，等.镜面投影法确定地球同步卫星精密轨道［J］.武汉大学学报(信息科学版)，2007，32(11):975－979.(Ou Jikun，et al.Determining precision orbit of a geostationary satellite GEO with mirror surface projection method［J］.Geomatics and Information Science of Wuhan University，2007，32(011):975－979)

15 袁运斌.基于GPS 的电离层监测及延迟改正理论与方法的研究［D］.中国科学院测量与地球物理研究所，2002.(Yuan Yunbin.Study on theories and methods of correcting ionospheric delay and monitoring ionosphere based on GPS［D］.Institute of Geodesy and Geophysics(IGG)，CAS，2002)