小尺度体反射系数近似公式研究

李胜军，高建虎，雍学善，王耀，魏新建

（1.中国石油勘探开发研究院西北分院，兰州730020；2.中国煤炭科工集团重庆研究院，重庆400039）

小尺度体反射系数近似公式研究

李胜军1，高建虎1，雍学善1，王耀2，魏新建1

（1.中国石油勘探开发研究院西北分院，兰州730020；2.中国煤炭科工集团重庆研究院，重庆400039）

AVO技术经过几十年的发展已成为石油勘探中的一种重要技术，针对非均质性油气藏的储层预测，AVO方法具有其他方法不可替代的作用。应用波动方程差分数值解方法，研究了横向变速小尺度体的AVO特征，讨论了横向小尺度体的宽度和速度变化对反射系数的影响，然后应用最小二乘法原理拟合出了反射系数变化量与小尺度体宽度和速度的数学表达式，并结合测试数据进行了误差分析。结果表明：拟合公式与测试数据之间的误差小于0.5%，较好地反映了小尺度体宽度及岩石弹性参数对反射系数的影响。该公式可为利用AVO异常来预测小尺度体的宽度和岩石弹性参数奠定基础，同时也为下一步横向小尺度变速情况下反射系数精确表达式的验证提供保障。

AVO；横向变速；小尺度体；反射系数；超定方程

0 引言

AVO技术是预测油气和估计地壳岩性参数的有效技术之一［1］。孙鹏远等［2］对基于Zeoppritz方程的各种近似公式的反射系数表达方法进行了归类和对比，发现目前大多数AVO研究是在均匀介质或各向同性介质前提下对Zeoppritz方程的近似研究［3-7］。但在已发现的油气田中，陆相碎屑岩油气藏占90%，其非均质性一般强于海相碎屑岩，我国海相碳酸盐岩缝洞型油气藏的非均质性较二者更强［8］，而且近年来倍受关注的火成岩油气藏也具有强非均质性。随着地质体非均质程度的增强，地球物理探测技术的难度逐渐增大，因此如何有效预测非均质储层是油气勘探开发中的一个关键环节［9-10］。现有的储层预测方法大多基于水平层状介质和均匀介质模型，不能满足非均质性储层预测的需求。因此，必须对非均质性储层的反射系数随介质弹性参数的变化情况进行深入的研究。

在横向均质或大尺度横向变速的情况下，Zeoppritz方程及其简化式可以很好地描述地层的反射系数。在小尺度横向变速的情况下，现有的反射系数表达式不能有效地描述地下介质的真实情况［11-12］。目前对小尺度横向变速情况下反射系数近似式的研究很少，而且主要是从各向异性的角度对Zeoppritz方程近似式进行修正，不能应用于实际的AVO分析和叠前反演中［13-15］。笔者采用全波场正演模拟算法对模型进行分析，探索了反射系数随小尺度体宽度变化的规律及其与岩石弹性参数的关系，初步确立了横向非均质储层中AVO特征与小尺度体宽度及岩石弹性参数的关系。

1 方法原理及模型分析

目前，一般使用厚层均质模型进行AVO分析，反射系数通过近似方程结合反射界面两侧的岩石弹性参数来求取。实际上地下介质在横向上的速度有可能变化，如果忽视它，就会影响到储层参数的预测精度。前人对于横向变速体反射系数的研究较少，尚未有横向小尺度变速情况下反射系数的近似公式，也未见成熟模型。笔者通过设计小尺度体内的岩石弹性参数模拟了地下介质的速度变化，并且改变小尺度体的宽度模拟了异常体的大小，实现了模型的简化，然后在均匀介质中加入1个尺度体（分别为λ，λ/2，λ/4和λ/8），应用波动方程数值模拟技术研究了横向变速小尺度体对反射系数的影响。

采用基于有限差分求解矢量波动方程的全波场数值模拟算法进行波场模拟，其中子波类型为Ricker子波，主频为30 Hz。为消除地震波传播的扩散影响，检波器放置在距离目标层50～100m处（图1），这样可以保证既记录入射波又记录反射波，从而估算每个波的慢度矢量方向，然后根据反射波与入射波的比值来绘制AVO曲线。图1（a）中上层介质参数为纵波速度2 192m/s、横波速度818m/s、密度2.160g/cm3，下层介质参数为纵波速度1543m/s、横波速度951.5m/s、密度1.973 g/cm3，小尺度体宽度为波长，小尺度体内纵波速度值依次从1 543m/s变化为1 550m/s，1 570m/s，1 580m/s和1 590m/s。对模型生成单炮记录［图1（b）］，并分别拾取入射纵波和反射纵波的振幅极大值，进一步可求取反射系数。通过改变小尺度体内的岩石弹性参数来研究其对小尺度体反射系数的影响，并通过改变小尺度体的宽度来研究其对反射系数变化规律的影响。

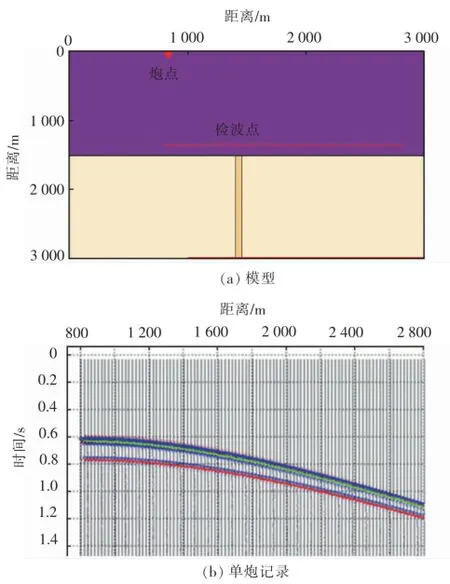
图1 小尺度体模型和单炮记录Fig.1 Small-scale bodym odeland shot recorder

图2 反射系数随入射角的变化Fig.2 Reflection coefficien t changew ith incidence angle

图2为小尺度体内速度变化时反射系数随入射角变化的关系曲线。可以看出，随着小尺度体内速度的增大，反射系数发生细微变化，而且绝对值减小。为进一步对比小尺度体内速度变化对反射系数的影响，根据变化前与变化后的速度残差做反射系数变化量与偏移距的关系图（图3）。

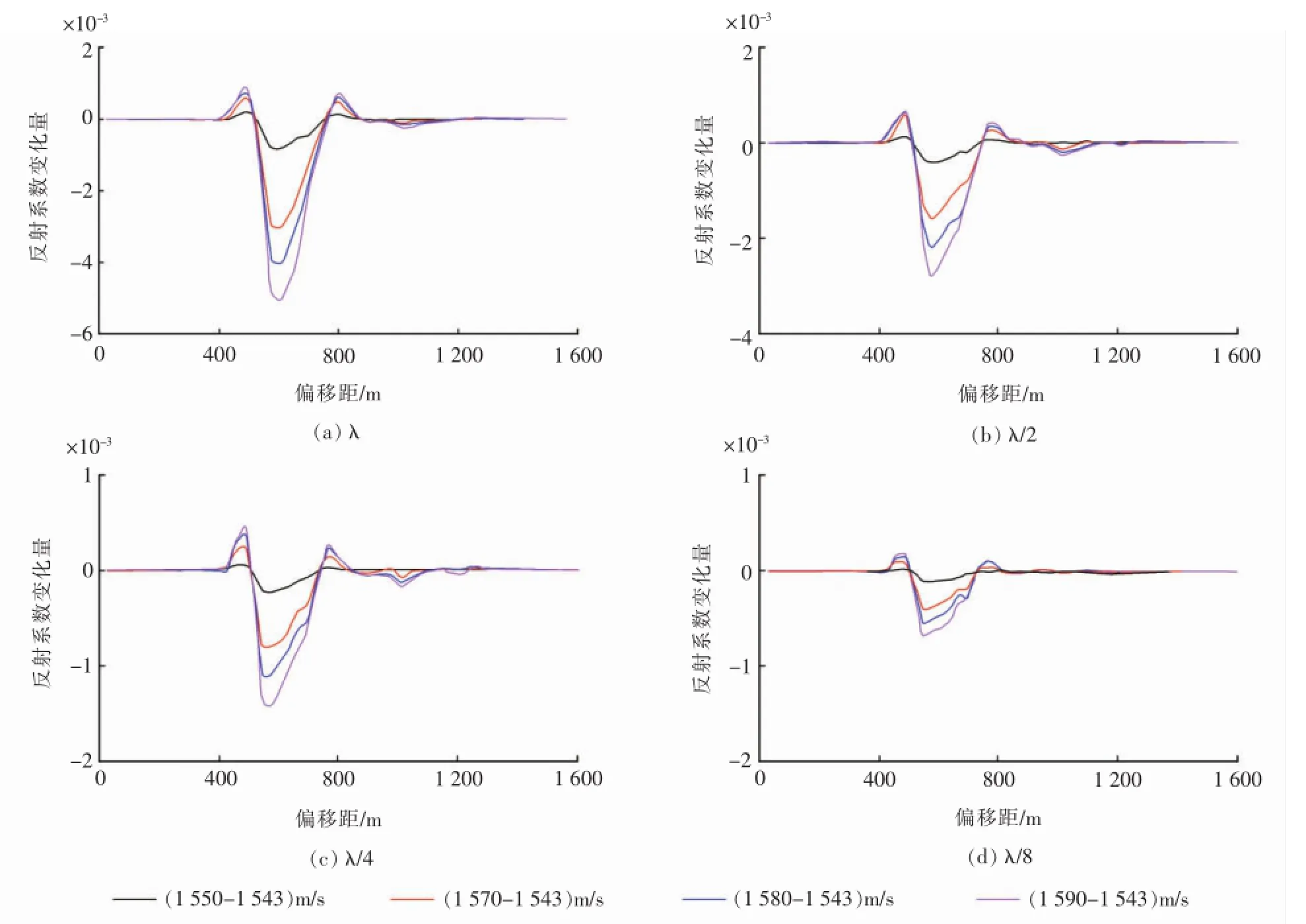
图3 反射系数变化量与偏移距的关系Fig.3 Relationship between reflection coefficientvariation and offset

从图3可以看出，随着速度残差的增加，反射系数变化量明显增大；小尺度体的宽度越小，相同速度残差下对反射系数的影响越小；当小尺度体宽度为λ/2时，反射系数变化量最大值约为0.003，当小尺度体宽度为λ时，反射系数变化量最大值约为0.005，前者比后者减小了40%，说明小尺度体的宽度对反射系数变化量的影响较为明显。

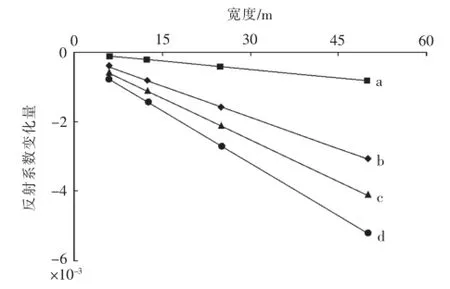
图4 小尺度体宽度与反射系数变化量的关系Fig.4 Relationship between the small-scalebodyw idth and reflection coefficient difference

2 近似公式

以不同尺度体宽度为横坐标，反射系数变化量为纵坐标，将上述模型对应的数值投影到直角坐标系中，并对不同阻抗差对应的值进行线性拟合（图4）。从图4的拟合公式可以看出，同一阻抗体对应的反射系数变化量与小尺度体宽度有很好的线性关系，反映拟合程度的确定系数的最小值也达到0.996，说明线性关系非常好。同样，对于相同宽度的小尺度体，其对应的阻抗差也与反射系数变化量呈线性关系。因此，由小尺度体引起的反射系数变化量是小尺度体对应的宽度及相应阻抗差的函数。通过大量模型数据的统计分析，得出公式：式中：ΔR为反射系数变化量，无因次；λ表示波长，m；xλ为小尺度体宽度，m；Δimp为小尺度体与围岩的阻抗差，g/cm3·m/s；a，b，c和d分别为待定系数。如果式（1）成立，那么就可根据反射系数的变化量进一步预测小尺度体的宽度及阻抗差。

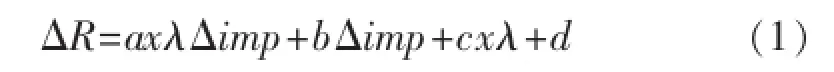
下面求解待定系数a，b，c和d。对于某一宽度的小尺度体，式（1）可变形为

对于上述4个不同宽度的尺度体，可形成关于axλ+b和cxλ+d的超定方程组。通过求解，可得出待定系数a，b，c和d，则式（1）可表示为

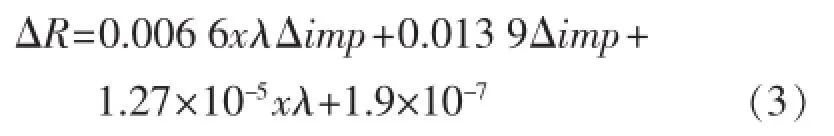
3 误差分析

由于参数是根据有误差的测试点计算出来的，它们之间不可避免地存在偏差，同时各个观测数据点不是完全准确地落在拟合线上，因此根据式（3）得到的计算值yi与实测值之间也就有偏差。利用式（3）对不同阻抗差及小尺度体宽度进行计算，反射系数变化量如图5所示（图中各条直线的含义与图3相同），图中直线表示由公式计算的不同阻抗差对应的反射系数变化量的趋势线，散点代表实测值。从图5可以看出，趋势线与实测点的分布之间存在不同程度的偏差。

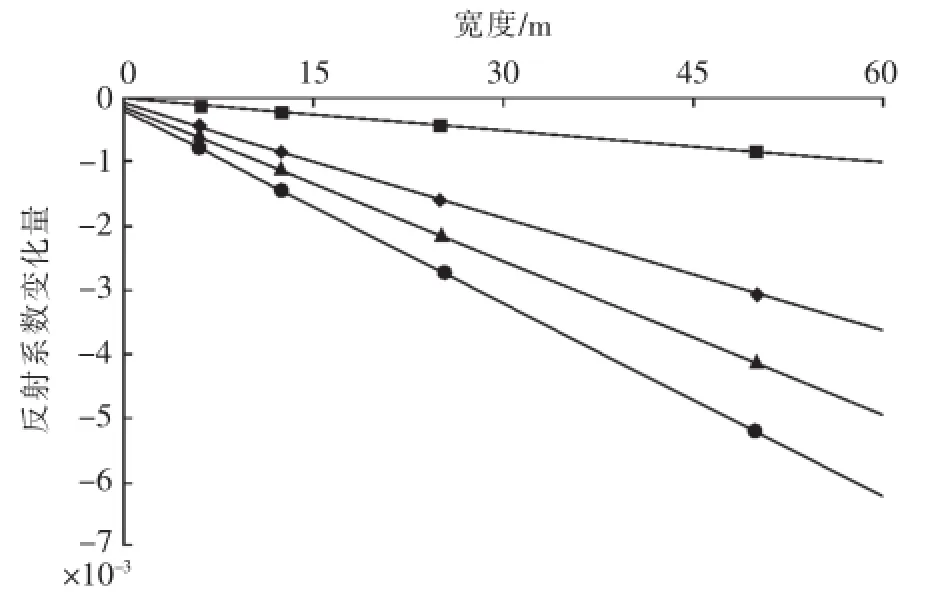
图5 拟合曲线图Fig.5 The fitting curves

趋势线与实测点的拟合程度通常用拟合优度来衡量，观测点越靠近回归直线则表示拟合程度越好。度量拟合优度的统计量是确定系数R2，计算公式为

其中

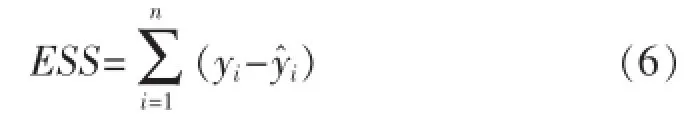
式（4）～（6）中：TSS表示总离差平方和；ESS表示残差平方和；yi表示实测值；y表示实测值的平均值；yi表示拟合计算值。

联立式（4）～（6），可计算出确定系数R2=0.99，说明拟合优度较高，证实上述拟合公式的拟合效果非常好。这也说明根据式（1）对不同小尺度体宽度及阻抗差引起的反射系数变化量计算的误差较小。

由于笔者设计的模型存在突变点以及模拟计算中采用的是差分模拟算法，这2个因素均会引起绕射波的存在，而在求解上述公式时，笔者利用小尺度体的中间值进行计算，最大限度地减小了因绕射引起的反射系数误差，因此反射系数的计算结果较为合理。

4 结论

（1）由横向小尺度变速引起的反射系数变化量与小尺度体的宽度和阻抗差均分别呈近似线性关系。

（2）通过超定方程求出了小尺度体的宽度和阻抗差分别与反射系数变化量的关系式，为小尺度体内岩石弹性参数的预测提供了理论依据。

（3）经过误差分析，得出线性拟合度为0.99，证实了预测公式的准确性。

［1］Marmalyevskyy N，Roganov Y，Kostyukevych A，et al.Frequency dependingAVO foragas-saturated periodical thin-layered stack［C］. NewOrleans：SocietyofExploration Geophysicists，2006：274-277.

［2］孙鹏远，孙建国，卢秀丽.P-P波AVO近似对比研究：定性分析［J］.石油地球物理勘探，2002，37（增刊1）：164-171.

［3］王建花.叠前弹性参数反演新方法［D］.青岛：中国海洋大学，2006.

［4］李胜军，高建虎，赵应成，等.横向变速小尺度体反射系数变化规律研究［J］.天然气地球科学，2011，22（5）：878-883.

［5］Ostrander W J.Plane-wave reflection coefficients for gas sands atnonormalanglesof incidence［J］.Geophysics，1984，49（10）：1637-1648.

［6］Andreas Ruger.P-wave reflection coefficients for transversely isotropicmodelswith verticaland horizontalaxisofsymmetry［J］.Geophysics，1997，62（3）：713-722.

［7］Vavrycuk V，Psencik I.PPwave reflection coefficients inweakly anisotropic elasticmedia［J］.Geophysics，1998，63（6）：2129-2141.

［8］羊屋三维处理、解释一体化方法研究组.VTI介质的AVO理论与应用研究［J］.石油地球物理勘探，2002，37（4）：363-371.

［9］阴可，杨慧珠.各向异性介质中的AVO［J］.地球物理学报，1998，41（3）：382-390.

［10］陆基孟.地震勘探原理（下）［M］.第2版.东营：石油大学出版社，2001：163-168.

［11］李胜军，孙成禹，高建虎，等.地震波数值模拟中的频散压制方法分析［J］.石油物探，2008，47（5）：444-448.

［12］李胜军，孙成禹，倪长宽，等.声波方程有限差分数值模拟的变网格步长算法［J］.工程地球物理学报，2007，4（3）：207-212.

［13］李胜军，高建虎，雍学善，等.球面波的反射P波AVO分析［J］.地球物理学报.2012，55（10）：3459-3466.

［14］李胜军，刘伟方，高建虎，等.正演模拟技术在碳酸盐岩溶洞响应特征研究中的应用［J］.岩性油气藏，2011，23（4）：106-109.

［15］李胜军，高建虎，张军舵，等.体纹理属性提取技术研究及应用［J］.地球物理学进展，2013，28（3）：1563-1569.

（本文编辑：涂晓燕）

Approximate formula of reflection coefficient for small-scalebody

LIShengjun1，GAO Jianhu1，YONG Xueshan1，WANG Yao2，WEIXinjian1
（1.PetroChina Research Institute ofPetroleum Exp loration&Development-Northwest，Lanzhou 730020，China；2.Chongqing Research Institute，China CoalTechnology&EngineeringGroup，Chongqing400039，China）

AVO technologyhasbecomean importantmeans for petroleum exploration after decadesofdevelopment.In theaspectof findingheterogeneous reservoir,AVO techniqueplaysan irreplaceable role compared with othermethods. This paper analyzed the AVO characteristics of the lateral variable small-scale body through wave equation finite differencenumericalsolutionmethod,and discussed the influencesofsize variation and speed changeof lateralsmallscalebodyon the reflection coefficients.The leastsquaremethodwasused to fit the relationsofthe reflection coefficient differencewith scalebodywidth and scale velocity.The resultoferroranalysis combined with testdata shows that the errorbetween fitted formulaand theexperimentdata is less than 0.5%,which indicates the influenceofsmall-scalebody width and elastic parameterson the reflection coefficient.The formula can beused topredict the sizeofsmall-scalebody and rock elastic parameters through AVO abnormalities,and provide protection for the validation of theexactexpression of reflection coefficientwith velocity changeof transverse small-scalebody.

AVO；lateralvelocityvariations；small-scalebody；reflection coefficient；overdetermined equation

P631.4 < class="emphasis_bold">文献标志码：A

A

1673-8926（2014）01-0096-04

2013-07-28；

2013-09-13

国家重大科技专项“天然气复杂储层预测与烃类检测地球物理技术研究及应用”（编号：2011ZX05007-06）和“海相碳酸盐岩储层地震描述与油气藏有效预测技术研究”（编号：2011ZX05004-003）联合资助

李胜军（1979-），男，硕士，工程师，主要从事地震波传播及正演模拟研究工作。地址：（730020）甘肃省兰州市城关区雁儿湾路535号。E-m ail：li_sj@petrochina.com.cn。