隧道开挖面空间效应特征研究及应用
2014-02-10姜彦彦姜建平
姜彦彦 姜建平 纪 宏
(济南市公路管理局 济南 250108)
随着我国经济的发展,地下空间开发利用的规模将逐步扩大,地下商场、地下综合交通枢纽、地下隧道、地下铁道等将在全国各地全面展开,地下空间开发将迎来高峰期[1]。在地下工程发展的同时,许多工程问题不断出现[2],而地下工程开挖面的时空效应问题就是这诸多问题之一。
在岩土体中开挖隧道,伴随着开挖面向前推进,荷载与约束实质上是处于一个在时间和空间上动态变化的过程,这势必对围岩产生影响。因此,可以说围岩的稳定不仅与最终状态有关,而且还与过程相关[3]。在这个过程中,围岩位移不断调整,尤其是围岩较好的硬岩隧道,隧道掘进时,开挖面空间效应更加显著。而对于小净距隧道,2个工作面之间在空间上产生的叠加效应,使位移分布形式更加多样,这不仅与施工的工序相关[5],而且与净距的大小密切相关。因此,在隧道开挖过程中,如何尽可能地减少对岩体初始状态的扰动使围岩处于相对稳定的状态[6],是非常复杂的问题,有必要对开挖面空间效应展开特别研究,这对于围岩稳定及对隧道的顺利施工起着至关重要的作用。
对开挖面空间效应进行研究的科技工作者很多,目前多采用粘弹性模型或粘弹塑性模型结合空间效应的流变属性进行分析,小净距隧道多将监控量测与数值模拟结合起来进行分析。
赵旭峰[7]计入围岩流变效应,考虑深部软岩隧道时空效应影响,得出在作业面影响范围内开挖面空间效应占主导因素;王军等[8]对不对称连拱隧道中墙的破坏机里进行了以监控量测为主的数据统计的方式来展开研究;李术才等[9]采用模型试验和数值模拟相结合的方法对分岔隧道进行了稳定性分析及施工优化方面的研究,得出不同中墙宽度及装药量大小时的优化方案;王者超[10]等对分岔隧道的变形监测展开研究得出针对小净距隧道的施工对策。
本文采用三维线弹性的有限元数值模拟,分别分析开挖面的空间效应,及小净距隧道开挖面的叠加效应,并结合现场监测数据,得出有实际意义的结论,见图1。
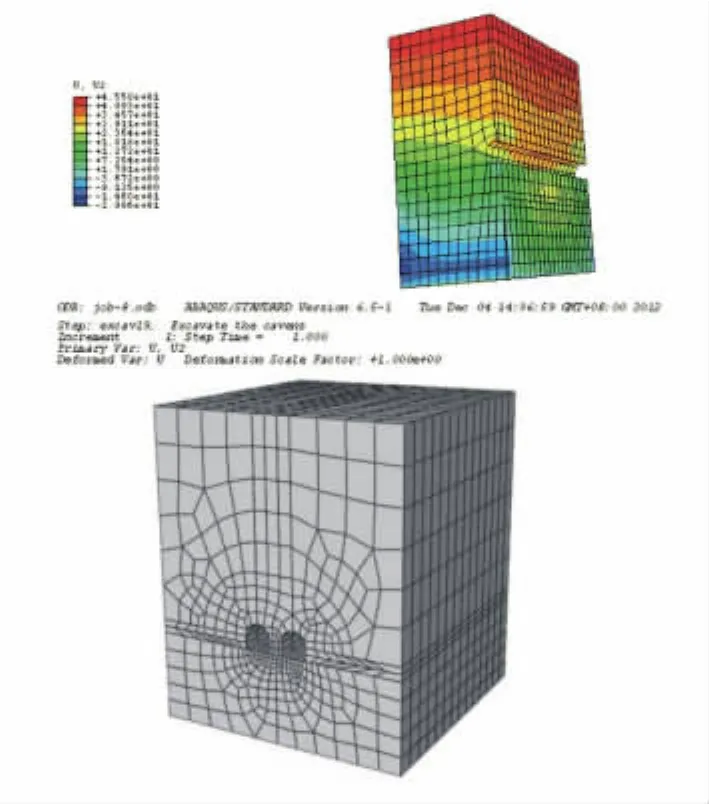
图1 单隧道和小净距双隧道三维有限元模型
1 研究方法
研究主要采用ABAQUS软件,选用20节点六面体单元即C3D20R单元类型对模型统一划分,假设岩体为线弹性,具体模型尺寸及相关物理参数见表1。物理参数的选取参考了相关实验数据和工程勘察资料。

表1 模型尺寸与相关物理参数
结合现场工程地质情况,所建模型初始地应力场为自重应力场。模型底部加竖向位移约束,两侧面加左右位移约束,前后面加前后向约束,共5处约束。隧道开挖前采用Geostress分析步进行地应力平衡。
2 隧道开挖面空间效应
2.1 单隧道拱顶沉降规律分析
为研究拱顶沉降全过程曲线,监控模型中间断面拱顶的沉降变化情况,得到随着开挖面向前掘进监测断面拱顶的沉降数据。图2为监测断面拱顶沉降变化曲线。由图2可见,隧道开挖时,在监测点处,即使岩体还未开挖,由于开挖面的向前掘进,监测点处已经产生了沉降,沉降量约为32.4%,而且在开挖面前后1倍洞径处沉降量较大,占到总沉降量的72.9%。
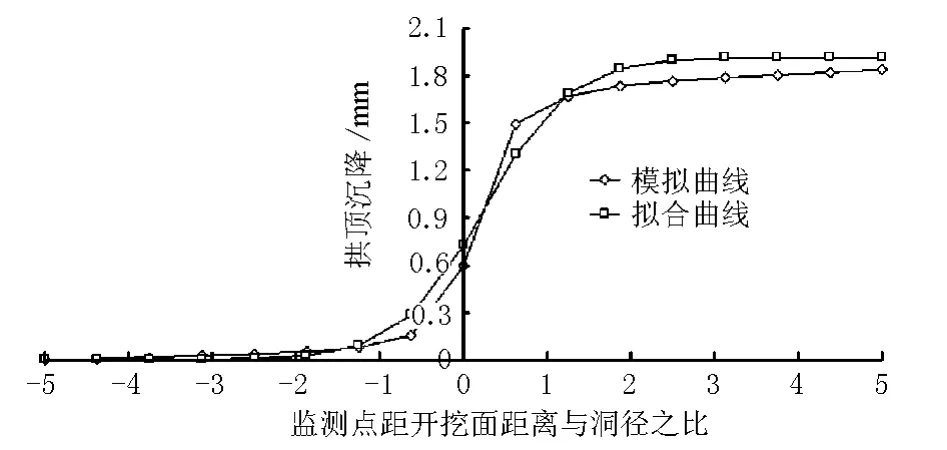
图2 拱顶沉降与其拟合曲线
所以监控量测只能根据工程现场条件得到部分变形曲线,而不能得到完整的变形曲线。
由于开挖面的空间约束效应,拱顶沉降是逐步释放的。开挖面的掘进导致隧道前方一定范围内围岩受到扰动,开始产生沉降。同时,由于开挖面空间约束作用,随着开挖面掘进,其后围岩应力逐渐释放,拱顶逐步下沉,当距开挖面一定距离时,洞室围岩变形不再受开挖面约束。
从模拟曲线中还可发现,曲线斜率在纵轴左侧大于右侧,说明开挖面对其前方岩体的约束效应大于其后方岩体。这一结果,也符合新奥法中的超前支护理论。
为了得到拱顶沉降与开挖面空间关系,采用式(1)拟合有限元模拟数据。

式中:S为沉降量;n=L/D为量纲~的量化开挖面与监测点距离,L为监测断面距开挖面距离;D为隧道洞泾。
其中:S0和c为参数。式(1)满足以下3个条件:
①当n→-∞时,S=0 (2)
②当n→+∞时,S=S0(3)
③当n=c时,S=S0/2 (4)
从上述式子不难看出,S0为隧道最终沉降量。
对式(1)分别求一次和二次导数,得
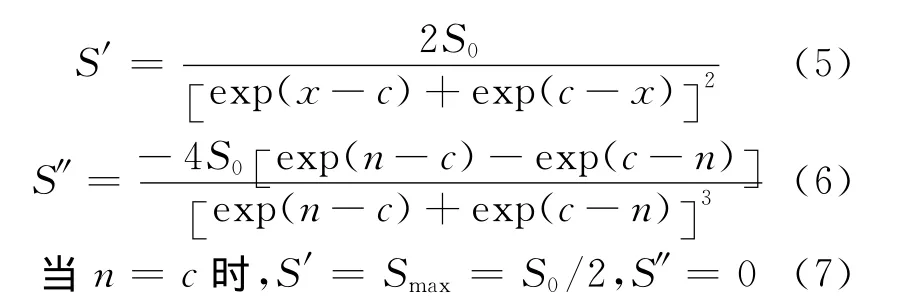
当n=c,曲线斜率最大。即开挖面开挖至此处时开挖单位长度隧道引起的拱顶沉降量最大。
将图2中数据与式(1)拟合,得S0=1.92 mm,c=0.25。
将c代入式(1),并令n=0得

即地下工程开挖面未开挖至监测断面时,发生的拱顶沉降量约占总沉降量的37.7%。
2.2 现场监控量测数据
图3为某巷道拱顶沉降典型监测曲线,监测采用水准仪进行。自巷道开挖至最终稳定巷道沉降值S观为2.76mm。而根据2.1研究结果,在巷道开挖至监测断面前,巷道拱顶已经发生了部分沉降。

图3 施工巷道后行侧0+180断面拱顶沉降曲线
假设c=0.25,则由式(8)得:Sn=0=0.377S0,因此S观=0.623S0。
图3曲线起始可视为n=0,则最终沉降量
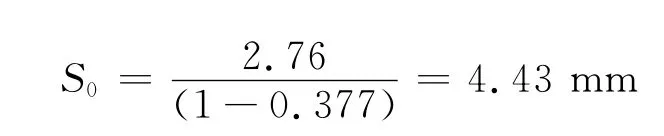
因此,围岩发生的总位移远大于监测所得位移。
图4为该断面拱顶沉降-开挖面距离全过程曲线与由公式(1)得到的当S0=4.43mm时的拟合曲线。从图4中可看出,在0~4倍洞径范围内,2条曲线出现较大差异。其原因有:
(1)拟合曲线假设,该取值是选用线弹性模型,未考虑时间效应情况下得到的,而实际情况下围岩本构关系较为复杂。
(2)模型未考虑现场施工条件,比如有爆破及其他人为操作所带来的振动荷载。

图4 拱顶沉降监测曲线与拟合曲线
目前,位移反分析是获取围岩参数的重要途径,在反分析中,一个重要的输入参数是围岩最终位移量。根据本研究结果,在本研究设定条件下,围岩发生的总沉降值约为监测值的1.6倍,即:S0=1.6S观。
3 小净距隧道工作面空间效应
随着高等级公路建设的迅猛发展,山区高速公路选线时上、下行隧道往往受地形限制,使得两相邻隧道的最小净距不能满足设计规范的要求。而连拱隧道的工程造价、施工难度、施工周期均比双线双洞隧道大得多,为此,在工程实践中衍生出小净距隧道。小净距隧道双洞的中夹岩墙宽度介于连拱隧道和双线隧道之间,一般小于1.5倍隧道开挖断面的宽度。由于间距较小,两侧隧道的相互影响作用是小净距隧道建设中需要特别关注的问题。
3.1 小净距隧道拱顶沉降规律分析
为研究小净距隧道拱顶沉降全过程曲线,分别监控两隧道中间断面拱顶沉降变化情况。图5为间距6m时,先行侧中间拱顶点竖向位移变化及后行侧中间拱顶点竖向位移变化的数值模拟曲线。
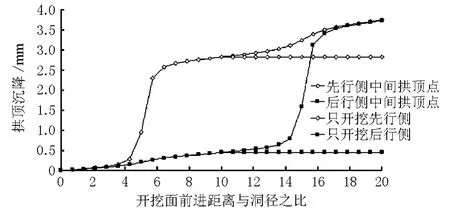
图5 双隧道先行侧、后行侧拱顶沉降模拟曲线
如图5所示(为便于表示,将先行侧0~120 m表示为0~10倍洞径,后行侧0~120m表示为10~20倍洞径 ),先行侧拱顶沉降曲线在0~10倍洞径范围与图2拱顶沉降曲线相似,10倍洞径之后为后行侧开挖对先行侧待测拱顶点沉降位移的影响。随开挖面在后行侧掘进,先行侧拱顶沉降进一步释放,位移曲线继续上升,在开挖面与待测点平行时,曲线斜率出现陡增,而后又渐渐趋于平缓。从后行侧拱顶沉降变化曲线中可看出,当开挖面在先行侧掘进时,后行侧就已经开始产生拱顶沉降。从图5中还可以看出2个开挖面空间约束效应叠加:在先行侧开挖完后,其变形已趋于稳定,但由于后行侧开挖面空间效应的影响,围岩应力状态经历了新的调整。表现为先行侧拱顶竖向位移曲线在开挖至15倍洞径处斜率上升,位移量加大。
图6为不同净距下,拱顶沉降分布曲线。从图6可看出,开挖面对相邻隧道竖向位移的空间约束效应随着两隧道净距的减小而增大。净距为8m时,后行开挖隧道开挖至12倍洞径时,先行侧拱顶位移曲线已趋于稳定。而随着净距的减小,后行隧道对先行隧道的影响增大,即后行隧道开挖面要掘进更远的距离,先行隧道拱顶点的竖向位移才会趋于稳定。所以小净距双隧道中,开挖面对相邻隧道竖向位移的影响非常大,当后行隧道开挖时,对于之前变形已监测稳定的先行隧道,仍要进行监控量测,以控制变形。且在施工作业时,两隧道进程应保持两倍洞径以上的距离,防止开挖面空间效应叠加,产生较大的位移变形。
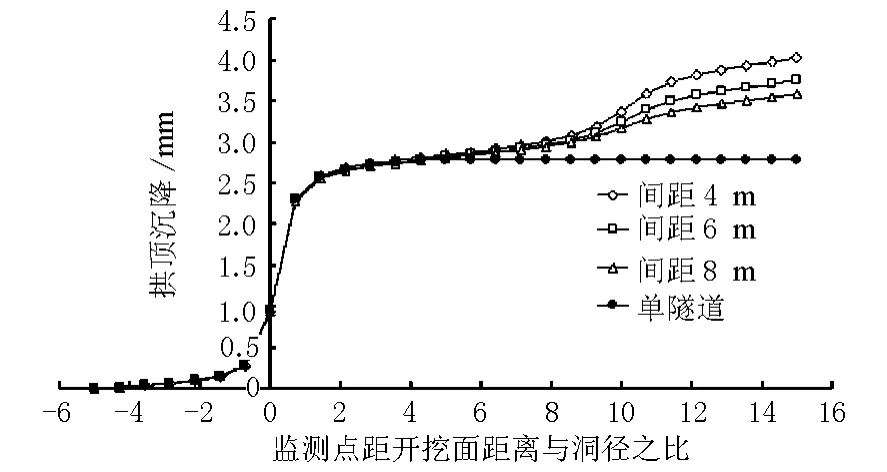
图6 小净距隧道先行侧中间拱顶点在不同净距下拱顶沉降曲线
3.2 现场试验数据分析
沪蓉国道主干线八字岭隧道小净距段某断面两侧隧道拱顶沉降监测数据如图7所示。该段隧道平均埋深约为100m,岩体以三叠系下统大冶组上段微晶灰岩为主。从图7中可以看出2个开挖面空间约束的叠加效应:开挖并支护完毕后,经过一段时间的应力调整,先行侧隧道在趋于稳定,但由于位于后行侧开挖面空间约束效应的影响范围,围岩应力状态经历了新的调整。表现为先行隧道拱顶下沉曲线在横坐标3~4倍洞径处出现一个陡增,下沉明显加大,但随着后行侧开挖面的掘进,影响逐渐减小,最后下沉曲线趋于稳定。现场监测结果显示小净距隧道两侧隧道相互影响,这与3.1节所获得的规律一致。
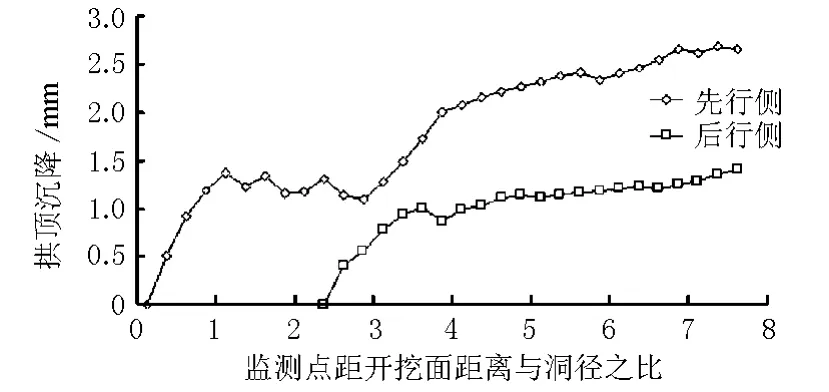
图7 双隧道中间拱顶点现场实测沉降变化曲线
4 结论
(1)单隧道拱顶沉降分布规律可采用式(1)进行简单描述。
(2)根据式(1)可推算地下工程围岩全部变形量与监测变形量的关系。
(3)在小净距隧道开挖的过程中,两侧隧道存在相互影响,且这种影响随间距减小而增大。
本研究成果可为地下工程位移反分析及稳定性评价提供一定依据。
[1] 姜彦彦.地下水封石油洞库风险分析与评价研究[D].济南:山东大学,2013.
[2] 王梦恕.中国铁路:隧道与地下空间发展概况[J].隧道建设,2010,30(4):352-354.
[3] 王梦恕.21世纪我国隧道及地下空间发展的探讨[J].铁道科学与工程学报,2004(1):8.
[4] 陈柚州,何文正,巩 雯.岩石隧道开挖面空间效应及其机理的研究[J].黑龙江科技信息,2010,26:302.
[5] 朱维申,李术才,白世伟,等.施工过程力学原理的若干发展和工程实例分析[J].岩石力学与工程学报,2003,22(10):1587-1588.
[6] 朱维申,王 平.岩体动态施工力学与动态规划原理在工程中的应用[J].水电站设计,1993 9(2):1-3.
[7] 赵旭峰,王春苗,孔祥利.深部软岩隧道施工性态时空效应分析[J].岩石力学与工程学报,2007,26(2):406-408.
[8] 王 军,夏才初,朱合华,等.不对称连拱隧道现场监测与分析研究[J].岩石力学与工程学报,2004,23(2):268-269.
[9] 李术才,王汉鹏,郑学芬.分岔隧道稳定性分析及施工优化研究[J].岩石力学与工程学报,2008,27(3):448.
[10] 王者超,李术才,陈卫忠.分岔隧道变形监测与施工对策研究[J].岩土力学,2007,28(4):788-789.
