非对称双线性对下的基于身份的加密方案*

2014-02-10许春根窦本年

通信技术 2014年8期

关键词：敌手私钥公钥

徐磊,许春根,窦本年

(南京理工大学理学院,江苏南京210094)

非对称双线性对下的基于身份的加密方案*

徐磊,许春根,窦本年

(南京理工大学理学院,江苏南京210094)

基于身份的加密是一种直接以用户的身份作为公钥的加密方案。自提出以来,利用双线性对实现基于身份的加密方案的案例已经有很多,但是这些方案大都是采用对称的双线性对,即要求作为映射输入的两个群相同。这无疑缩小了映射中所选取的椭圆曲线的范围,将在一种更一般的条件下,即在非对称双线性对下,基于判定性双线性Diffe-Hellman(BDHE)难解问题在标准模型下构造出一种新型的基于身份的加密方案,并证明其在标准模型下具有不可区分的选择身份的选择明文(IND-sID-CPA)安全性。

基于身份的加密方案非对称双线性对标准模型公钥加密

0 引言

基于身份的加密体制[1]提供了一种直接以接受者的家庭住址,电话号码等信息作为公钥的加密方法。这种体制自提出以来就受到了广泛的关注,因为与传统的公钥加密体制相比,基于身份的加密体制的公钥不需要认证中心认证,这大大减少了证书分发与管理的复杂性。在2002年,Dan Boneh[2]用双线性对构造出了第一个完整方案以后,大批学者利用双线性对中的困难问题相继构造出了一系列基于身份的加密[3-7],基于身份的分层加密[8-10]及签名[11-14]方案。但这些方案大部分都是在对称的双线性对下进行的,即要求G=,这种限制使得可以用来构造基于身份的加密方案的椭圆曲线种类受到了很大的限制,安全性也降低了很多。为了解决这个问题,Dan Boneh在2010年又提出了在非对称的双线性映射条件下,构造出标准模型下的一种新型的有效的基于身份的加密方案[15]。这种方案降低了双线性函数对椭圆曲线选择的限制,且有更好的安全性。本文将围绕这一思想给出一个安全的有效的加密方案。

1 基础知识

1.1 双线性对及其上的困难问题

为了构造我们所需的方案,这里先介绍双线性映射及双线性群。我们使用[4,15]中的定义:

设G,,Gt是3个阶为大素数p的乘法循环群。g∈G,∈分别是G,的生成元。e:G×→Gt是从(G,)到Gt的一个映射。称e:G×→Gt是一个双线性映射,如果:

1)映射e:G×→Gt可以被有效计算。

2)双线性:对所有的u∈G,v∈,a,b∈ZP,有e(ua,vb)=e(u,v)ab。

3)非退化性:e(g,)≠1。

上述是双线性对的基本定义,一般情况下,我们对G和没有太多的限制,即认定G=,且大部分的密码学方案也是在此前提下构造的,但是这限制了构造方案的广泛性,因此这里我们将在一个更加广泛的条件下构造出我们的加密方案,即不要求G=。这就使得我们可以利用的椭圆曲线的范围更加广泛,且方案会有更好的安全性。

现在我们给出非对称情况下的基于双线性的Decision-BDH问题DBDH的困难性假设。

(Decision-BDH)问题:给定(g,,ga,gc,a,b,Z)∈G3×3×Gt,其中g∈G,∈,Z∈Gt。对于未知的a,b,c∈ZP。判定e(g,)abc=Z是否成立。通常,对于多项式时间敌手A,和构造的算法B,将其针对群(G,,Gt)上的DBDH问题的优势定义为:

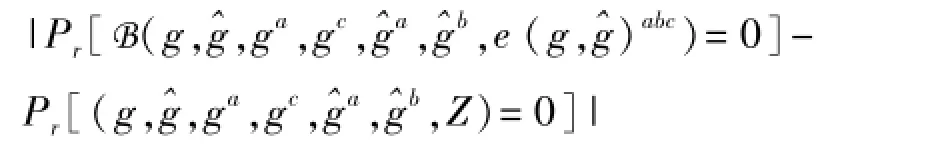
(DBDH)假设:若对于任意多项式时间t敌手A,和构造的算法B,其针对群(G,,Gt)上的DBDH问题的优势均小于ε,则称(G,,Gt)上的(t,ε)-DBDH假设成立。

1.2 基于身份的加密体制及其安全性描述

(基于身份的加密体制)一个基于身份的加密方案有下面4个随机算法组成:

Setup:挑战者输入安全参数k,返回系统参数params和系统主密钥msk。其中系统参数params作为系统参数公开,主密钥msk由PKG秘密保存。

KeyGeneration:将params,msk,以及用户的身份ID={0,1}*作为输入,返回一个私钥d。这里ID是一个任意长度的字符串,将被作为系统参数用来加密,d由用户自己保存,作为解密密钥。

Encryption:将params,ID,M∈M作为输入,返回密文C∈C。

Decryption:输入params,密文C,私钥d,输出明文M。

(攻击游戏)我们在选择身份攻击下使用敌手与挑战者游戏定义IBE的安全性,游戏规则如下:

Init:敌手A先给定一个他想挑战的身份ID*=。

Setup:挑战者运行Setup算法,将得到的系统参数params发送给敌手,私钥msk自己保存。

Phase1:敌手询问q1,q2,…qm,其中qi是下面描述:

-Extraction query＜IDi＞:挑战者通过运行Extract算法对敌手的询问返回对应于身份IDi的私钥di。然后把它发送给敌手。

Challenge:一旦敌手确定Phase1结束,立刻输出他想挑战的两个长度相等的明文M0,M1∈M。挑战者随机选取β∈{0,1},并且令挑战密文

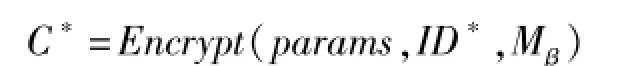
再将密文C*发送给敌手。

Phase2:敌手提出更多的询问qm+1,qm+2,…,qn,这里qi为下面情形:

-Extraction query＜IDi＞:这里IDi≠ID*,挑战者如Phase1做出回应。

Guess:最后,敌手输出猜测β′∈{0,1}。如果β′=β,敌手获胜。

2 基于身份的加密算法的构造

Setup:系统参数由下述方法生成,对生成元对为(g,)的双线性对(G,),随机选取α∈Zp,设g1=gα,1=α,随机选取∈及长度为n的向量W=(i),i∈。再随机选取β∈Zp,令0=αβ,并计算v=e(g,0)=e(g,)αβ。最后,公开系统参数params={G,,Gt,g,,g1,1,v,W},保留系统主密钥0。

KeyGeneration:设ID={I1,I2,…,In}是一个n比特的字符串代表身份,U⊆{1,2,…,n}是满足Ii=1的所有i的集合。则基于身份ID的密钥按如下路径生成:首先随机选取r∈Zp,用户ID私钥构造如下:

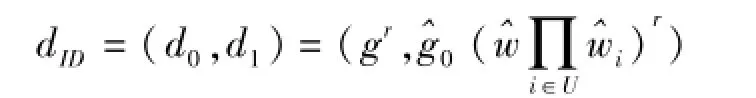
Encryption:设M∈Gt,则对于身份为ID的用户加密过程为:随机选取t∈Zp,然后利用公共参数构造密文如下:

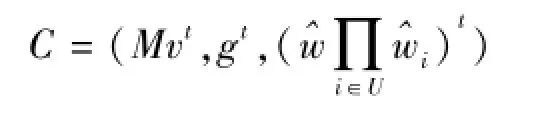
Decryption:设C=(C1,C2,C3)是消息M在身份为ID的用户下加密的密文。则C可以用dID解密,过程如下:

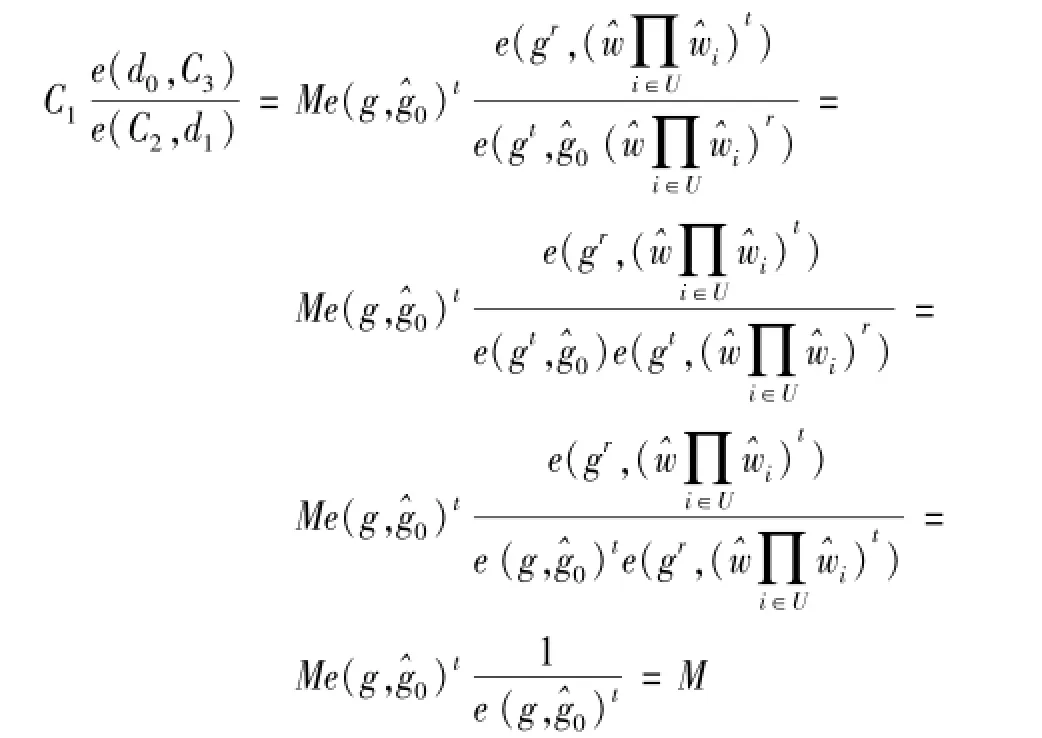
由此可知,该方案是可执行的。

3 安全性分析

我们在标准模型下,利用(G,,Gt)上的DBDH假设证明构造的IBE方案的安全性。先给出如下定理:

定理4.1:假设(G,,Gt)上的DBDH假设成立。则前面所定义的IBE方案对任意的qID次询问是具有(t′,qID,ε)-选择身份选择明文安全性(IND-sID-CPA)。

具体的说,如果针对上述方案,A是一个具有ε优势的(qID-IND-sID-CPA)敌手。那么存在一个(G,,Gt)上的DBDH敌手B使得其在游戏中与A有大致相同的优势ε。

证明:假设敌手A攻击IBE方案的优势为ε。我们构造一个算法B,它能够解决(G,)上的DBDH问题。算法B被给定一个随机的7元组(g,,ga,gc,a,b,Z)作为输入,7元组从PBDH(Z=e(g,)abc)或RBDH(Z在Gt中是独立同分布的)中选取。算法B的目标是:如果Z=e(g,)abc,输出β=1。否则,输出β=0。为了进行如下游戏,令g1=ga,1=a,g2=gc,2=b,则与敌手A互动的选择身份的游戏如下:

Initialization:此游戏从敌手A先选择一个他想攻击的身份ID*=开始。

Setup:为了生成系统参数,算法B设m=4qID,再随机选取k∈{0,1,…,n},以及长度为n的向量h=(hi)和h′,z′,其中h′以及向量h中的元素均取自于0到m-1,记H*=(h′,h)。再选取z=(zi),z′,向量z中的元素及z′均在Zp内取值。这些值都仅限算法B自己知道。

然后,对于身份ID={I1,I2,…,In},我们设U⊆{1,2,…,n}是满足Ii=1的所有i的集合。为了分析简便,我们定义下面3个函数:

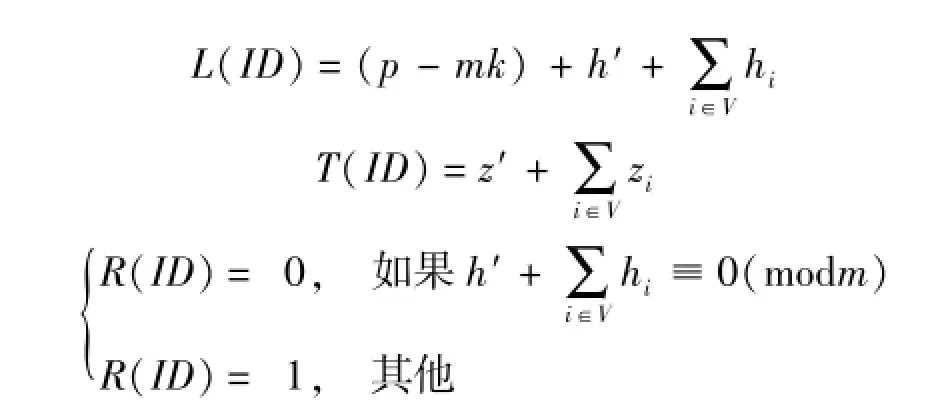
Phase1:敌手A询问私钥。假设敌手询问身份ID的私钥。如果R(ID)=0,则B中止游戏并随机输出β的猜测值β′。

否则,B随机选取r∈Zp,然后构造密钥:

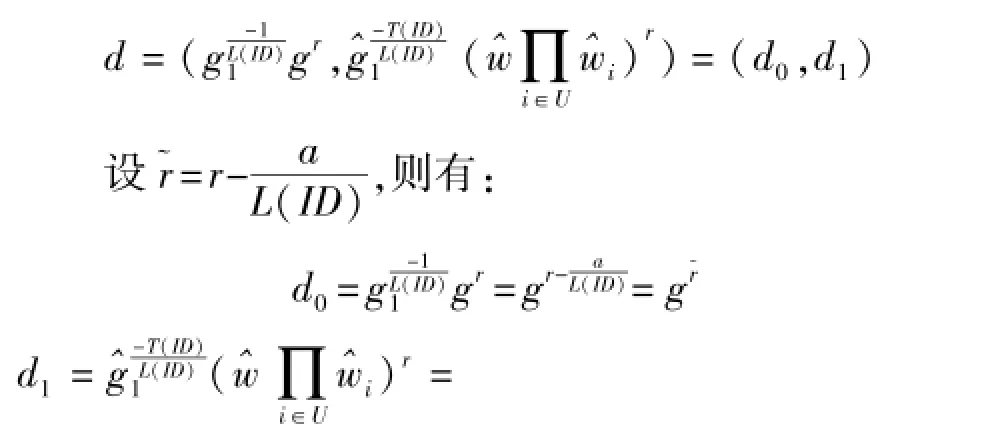
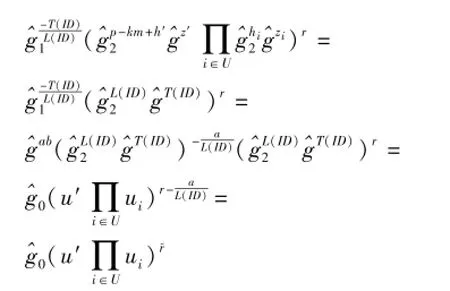
当且仅当L(ID)≠0(modp)时,算法B才进行如上计算,为了分析方便,我们设该游戏继续进行下去的充分条件为R(ID)≠0。

Challenge:当Phase1结束,敌手B立刻输出他想挑战的两个长度相等的明文M0,M1∈M。如果,则算法B随机选取一个猜测β。否则,随机选取γ∈{0,1},构造密文

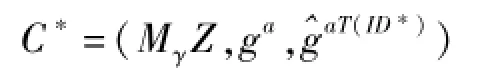
此时,C*是在敌手选择的公钥ID*=下对密文Mγ的一个有效加密。

另一方面,如果我们说Z是Gt中的任意一个元素。那么所得到的的密文将不会给出任何与γ相关的信息。

Phase2:敌手重复Phase1,提出更多的询问。算法B做出同前相应的返回输出。

Guess:最后,敌手A输出猜测γ′∈{0,1}。算法B输出如下游戏结果:

如果γ′=γ,敌手获胜。输出1,即意味着Z=e(g,)abc成立。否则输出0,谕示着Z≠e(g,)abc。

当B的7元组输入来自PBDH时,从A的角度上,这个算法B就等同于一次真实攻击,且A必须满足。

当B的7元组输入来自RBDH时,则敌手A的优势是可忽略的,即,因此a,b,c是均匀取自Zp中的,Z在Gt中也是随机选取的,这时候我们有:则定理4.1得证。

4 结语

文中介绍了利用非对称的双线性对在标准模型下构建一个IBE加密方案,并基于Decision-BDH难解问题,给出了其具有选择身份的选择明文安全性的证明。该方案不仅使得构建加密方案使用的椭圆曲线更加广泛,使得攻破的难度增加许多。而且具有很好的拓展性,比如可以将其演变成标准模型下基于身份的分层加密方案,还有随机预言模型下的一些加密方案等。后面我们还将着手分别在对称和非对称的双线性对模式下构造出更多的具有更多性质的加密方案[16-17],并给出与其相对应的签名,匿名签名[18],环签名[19]以及签密方案。

[1] SHAMIR Adi.Identity-Based Cryptosystems and Signature Schemes[C]//Advances in Cryptology-CRYPTO’84,LNCS(196).Berlin Heidelberg:Springer-Verlag, 1985:213-229.

[2] BONEH Dan,FRANKLIN Matt.Identity-Based Encryption from the Weil Pairing[C]//Advances in Cryptology Crypto 2001,LNCS(2139).Berlin Heidelberg:Springer-Verlag,2001:213-229.

[3] BONEH Dan,BOYEN Xavier.Efficient Selective Identity-Based Encryption without Random Oracles[C]//Advances in Cryptology-EUROCRYPT 2004,LNCS(3027).Berlin Heidelberg:Springer-Verlag,2004:223-238.

[4] WATERS Brent.Efficient Selective Identity-Based Encryption without Random Oracles[C]//Advances in Cryptology-EUROCRYPT 2005,LNCS(3494).Berlin Heidelberg:Springer-Verlag,2005:114-127.

[5] 周楝淞,杨洁,谭平嶂,等.基于身份的密码系统及其实现[J].通信技术,2010,43(06):68-70.

ZHOU Lian-song,YANG Jie,TAN Ping-zhang,et al.Implementation of Identity-based Cryptosystem[J].Communications Technology:2010,43(6):68-70.

[6] SAHAI Amit,WATERS Brent.Fuzzy Identity-Based Encryption[C]//Advances in Cryptology-EUROCRYPT 2005,LNCS(3494).Berlin Heidelberg:Springer-Verlag,2005:457-473.

[7] GALINDO David.Chosen-Ciphertext Secure Identity-Based Encryption from Computational Bilinear Diffie-Hellman Pairing[C]//Pairing-Based Cryptography-Pairing 2010,LNCS(6487).Berlin Heidelberg:Springer -Verlag,2010:367-376.

[8] HORWITZ Jeremy,LYNN Ben.Toward Hierarchical I-dentity Based Encryption[J].EUROCRYPT:2002, LNCS(2332):466-481.

[9] GENTRY Graig,HALEVI Shai.Hierarchical Identity Based Encryption with Polynomially Many Levels[C]// TCC 2009,LNCS(5444).Berlin Heidelberg:Springer-Verlag.2009:437-456.

[10] 张席,杨玲.一种高效的基于身份的分层加密方案[J].计算机工程与与应用,2012,48(24):101-105.

ZHANG Xi,YANG Ling.Efficient Hierarchical IDBased Encryption Scheme[J].Computer Engineering and Applications:2012,48(24):101-105.

[11] 刘振华,胡予濮,牟宁波,等.新的标准模型下基于身份的环签名方案[J].电子与信息学报,2009, 31(07):1727-1731.

LIU Zhen-hua,HU Yu-pu,MU Ling-bo,MA Hua. New Identity-Based Ring Signature in the Standard Model[J].Jounal of Electronics&Information Technology:2009,31(7):1727-1731.

[12] 徐国愚,陈性元,杜学绘.大规模延迟容忍网络中基于分级身份签名的认证方案研究[J].电子与信息学报,2013,35(11):2615-2622.

XU Guo-yu,CHEN Xing-yuan,DU Xue-hui.An Authentication Scheme Using Hierarchical Identity Based Signature in Large-scale Delay Tolerant Networks[J]. Jounal of Electronics&Information Technology:2013,35 (11):2615-2622.

[13] BONEH Dan,BOYEN Xavier.Short Signatures without Random Oracles[C]//Advances in Cryptology-EUROCRYPT 2004,LNCS(3027).BerlinHeidelberg: Springer-Verlag,2004:56-73.

[14] ZHOU Cai-xue,WAN Zhou,XI Wei-dong.Provable Certificateless Generalized Signcryption Scheme Designs [C]//Codes and Cryptography,71(2).Berlin Heidelberg:Springer-Verlag,2014:331-346.

[15] BONEH Dan.Efficient Selective Identity-Based Encryption without Random Oracles[C]//Journal of Cryptology 2011,LNCS(24).Berlin Heidelberg:Springer-Verlag,2011:659-693.

[16] SU Le,LIM Hoon-wei,LING San,WANG Huaxiong.Revocable IBE Systems with Almost Constant-Size Key Update[C]//Pairing-Based Cryptography Pairing 2013,LNCS(8365).BerlinHeidelberg: Springer-Verlag,2014:168-185.

[17] HOHENBERGER Susan,WATERS Brent.Online/Offline Attribute-Based Encryption[C]//Public-Key Cryptography-PKC 2014,LNCS(8383).Berlin Heidelberg:Springer-Verlag,2014:293-310.

[18] CHEN Jie,LIM Hoon-wei,SAN Ling,WANG Huaxiong,HOETECK Wee.Shorter IBE and Signatures via AsymmetricPairings[C]//Pairing2012,LNCS (7708).Berlin Heidelberg:Springer-Verlag,2013: 122-140.

[19] LIBERT Benoit,JOYE Marc.Group Signatures with Message-Dependent Opening in the Standard Model [C]//Cryptology CT-RSA 2014,LNCS(8366).Berlin Heidelberg:Springer-Verlag,2014:286-306.

XU Lei(1990-),male,M.Sci.,majoring in information security,modern cryptography and algorithmic analysis.

许春根(1969-),男,博士,教授,主要研究方向为信息安全与编码、密码技术应用研究;

XU Chun-gen(1969-),male,Ph.D.,professor,principally working at information security and codes,modern cryptography technology research.

窦本年(1976-),男,博士,讲师,主要研究方向为计算机应用技术、多用户环境下数字签名的构造。

DOU Ben-nian(1976-),male,Ph.D.,lecturer,mainly working at computer application technology,multi-users environment digital signature schemes.

Identity-Based Encryptionfrom the Asymmetric Bilinear Pairings

XU Lei,XU Chun-gen
(School of science,Nanjing university of science and technology,Nanjing Jiangsu 210094,China)

Identity-based encryption is a method which directly uses the user’s identity as its public key. Since it appears,there are a lot of identity-based encryption schemes from bilinear pairings,but most of these schemes uses symmetric bilinear pairings as their math tools,namely the groups as it put in the bilinear mapping should be the same one.This would greatly reduce the scope of the available elliptic curves in the encryption schemes.This paper proposes a new type of identity-based encryption scheme from the asymmetric bilinear pairings without using random oracles,in a more general bilinear pairings conditions, and proves that it has indistinguishable selective-ID CPA security by reducing it to decision-BDH problem under the standard model.

identity-based encryption;asymmetric bilinear pairings;standard model;public-key encryption

TP309

1002-0802(2014)08-0941-05

10.3969/j.issn.1002-0802.2014.08.020