支持向量机和BP网络在Mg/PTFE性能预测中的比较

赵田安, 欧阳的华, 刘 振

(武警工程大学 装备工程学院, 陕西 西安 710086)

0 引 言

随着火箭技术的不断发展，对固体推进剂的性能要求也越来越高。因此，对现有的推进剂的改进和各种新型推进剂的研制已成为广泛关注的焦点。烟火型贫氧推进剂是在烟火药的基础上发展起来的一种固体推进剂。作为一种非均质的贫氧推进剂，它与常规的贫氧复合推进剂(主要有碳氢燃料配方、含金属燃料配方和含硼配方三大类)相比，表现出许多优点：配方可调性大、燃温高，在较短的补燃室内和较低的压力下易于二次然烧，特别是用作固体火箭冲压发动机燃料不仅经济性好，而且能大大提高比冲[1]，镁/聚四氟乙烯(Mg/PTFE)贫氧推进剂就是其中的一种[2-6]。

目前，已有针对Mg/PTFE体系的Ladouceur和Kubota燃烧数值模型[1]以及相关理论的研究等[7]，但由于其燃烧反应过程十分复杂，此类研究仅限于局部参数在有限条件下的模拟运算，理论模型大都建立在各种假设和约束条件之上，涉及到的因素较少，不足以指导其性能的预测和配方的优化[8-10]。

为了探索不同的神经网络模型在Mg/PTFE贫氧推进剂性能预测中的作用，以便减少实验工作量和优化配方，本文分别采用BP网络和SVM网络不同配比、不同粒径、不同黏合剂含量的Mg/PTFE贫氧推进剂性能进行预测，以期通过预测结果的对比分析找出一种最合适的神经网络进行配方设计与性能预测的应用，为今后进一步的研究奠定基础。

1 神经网络用于性能预测的基本原理

1.1 BP神经网络

BP神经网络也称误差反向传播神经网络，为一种有导师的学习，是梯度下降法在多层前馈网络中的应用。它有一个输入层、一个输出层、一个或多个隐含层。每一层上包含若干个节点，每个节点代表一个神经元。同一层上的各节点之间无连接关系，相邻层采取全互连。上一层的输出作为下一层的输入，且每层节点仅能影响其下一层节点。典型的模型结构如图1所示。信息从输入层开始在各层之间单向传播，依次经过各隐含层，最后到达输出层。

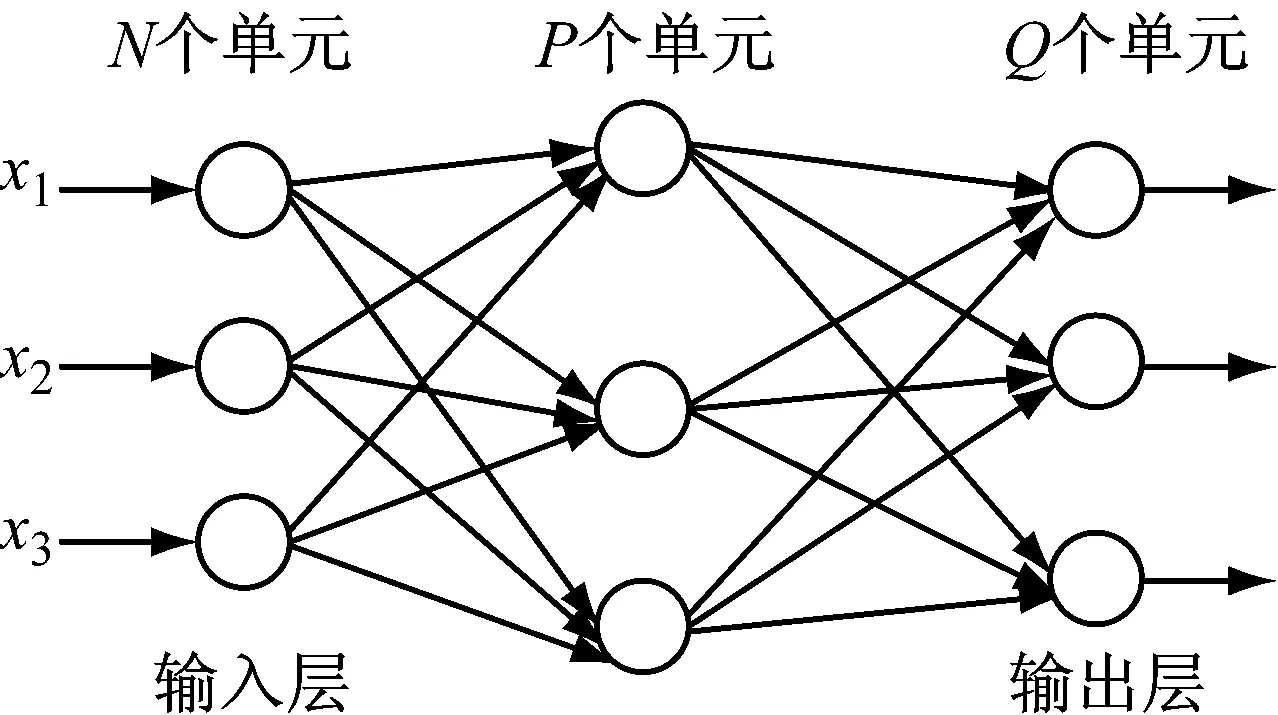
图1 BP网络结构示意图

BP网络的学习过程可分为信息的正向传播和误差的反向传播两部分。其算法的基本思想是根据网络输出层的误差，从输出层开始反过来调整网络的权值和阀值，最后使得输出的均方误差最小。以此为目标，对一定的样本进行“学习后”，网络所持的权值便是网络通过自适应学习得到的正确的内部表示。这时将待识别样本的特征数据输入训练好的网络，则网络就可以对样本的属性进行自动推理、识别[11]。

1.2 SVM网络

基于SVM网络的性能预测，就是利用SVM网络对试验数据(X，Y)进行学习，从而建立起由向量X到向量Y的非线性映射f，实现输入向量X即可预测与之对应的Y值的目的。SVM训练回归表达式为

(1)

通过核隐式映射，将输入空间X与输出空间Y联系起来，非线性函数则可以通过核特征空间中的线性学习器得到。实际上，这个算法又称为核岭回归，其解称为正则化网络，其正则算子通过核隐式选择，其中相应的SVM的训练网络如图2所示。

在使用SVM进行Mg/PTFE推进剂性能预测时，核的选择对于SVM训练回归具有重要意义，经过前期的实验，本文使用径向基函数(RBF)核进行回归训练，其表达式为

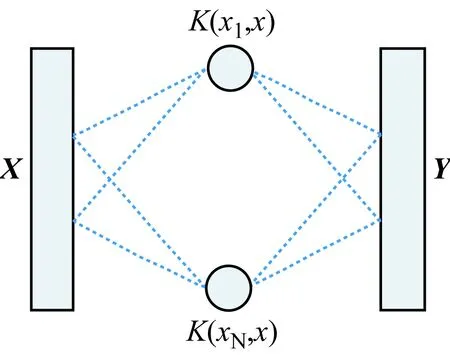
图2 SVM训练回归网络

(2)

σ2为核的方差，此时需要选择的参数有：不敏感系数ε、惩罚参数C及核参数γ。依据研究对象的特点，采用交叉验证的思想对SVM参数进行选择[12-15]，由于需要优化的参数不止一个，因此，同时采取了遗传算法来寻找这些参数的最优值。将ε、C和γ通过编码生成染色体种群，将训练样本集也划分为学习样本和检验样本，先用学习样本建立网络模型，再对检验进行预测，以预测相对误差作为目标函数进行最小化寻优，最后将寻优结果通过解码用于SVM网络对Mg/PTFE推进剂性能的预测。

2 基于神经网络的Mg/PTFE贫氧推进剂的性能预测

本文把Mg/PTFE贫氧推进剂配方的数学模型看作一个多输入多输出的映射关系f：

Y=f(X)

(3)

式中:Y为Mg/PTFE贫氧推进剂的3种主要性能参数——燃烧热、燃烧温度和燃烧速度,

Y=(Q,T,r)

(4)

X为影响Mg/PTFE贫氧推进剂性能的4种因素，即PTFE/Mg配比、黏合剂含量、镁粉粒径、PTFE粒径：

X=(α1,α2,d1,d2)

(5)

本文的主要研究内容就是利用BP神经网络和SVM对试验数据对(X,Y)进行学习，建立起由向量X到向量Y的非线性映射f，实现输入向量X即可预测与之对应的Y值的目的。

2.1 训练及预测结果验证用实验数据的获取

在设计试验时，考虑到网络模型的精度和泛化能力在很大程度上取决于训练样本的准确性和完备性，因此训练数据的合理性是建立良好网络模型的重要前提。为了得到较为合理的训练数据，试验时采用均匀设计的方法来获取试验点，以保证训练样本的完备性和均匀性。采用YX ZR/Q金鹰全自动量热仪，德国IMPAC公司生产的IGA-140型非接触式远红外测温仪和高速摄影法对Mg/PTFE贫氧推进剂(15 g )的燃烧热,燃烧温度和燃烧速度在常温、常压下进行了测试，具体结果见表1。

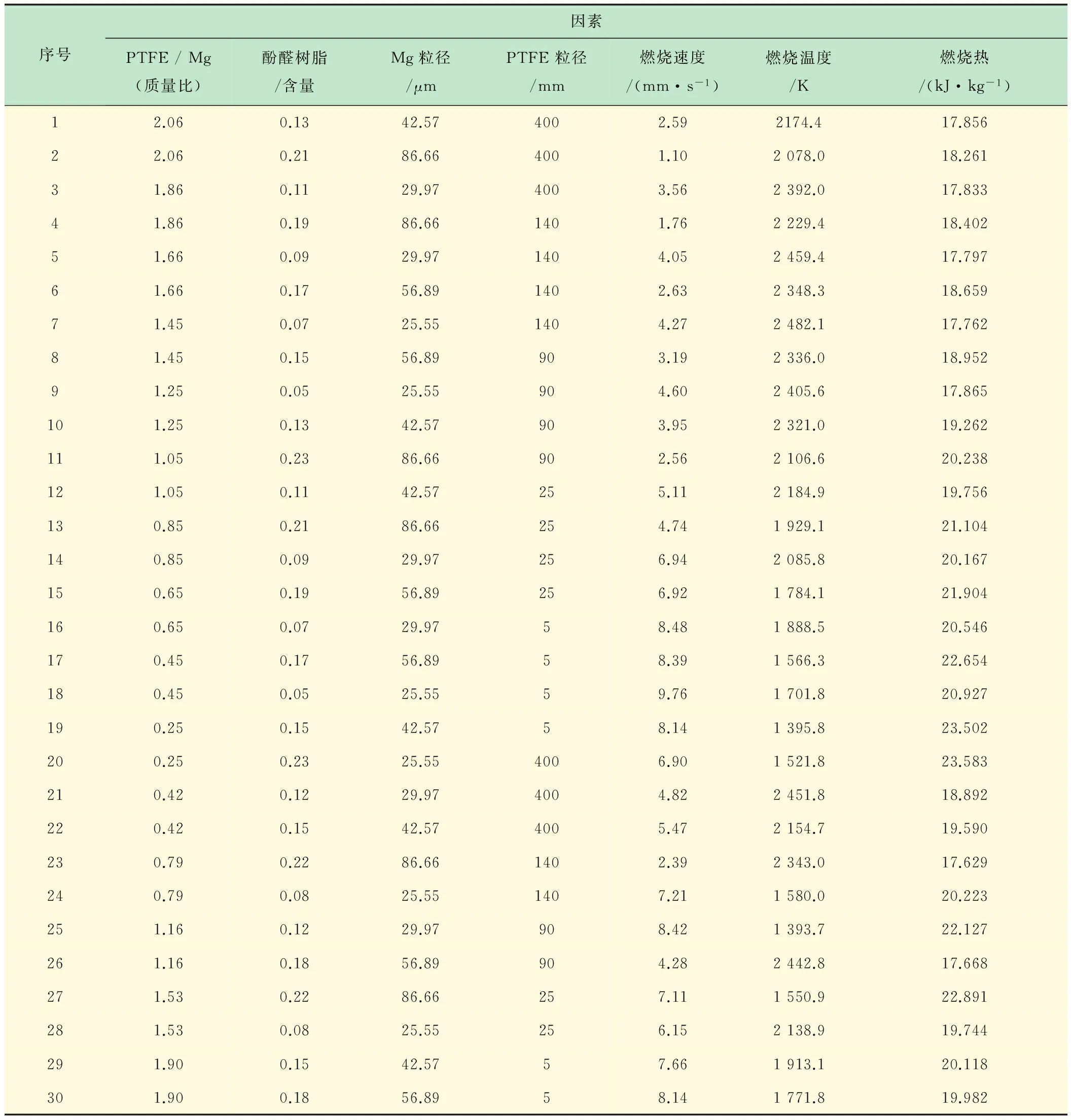
表1 Mg/PTFE烟火药配方

2.2 训练用数据的预处理

对于N个样本的集合{(Pk,Tk)|P∈Rm,T∈Rn,k=1,2,…,N}，在利用神经网络建立起P、T这两个离散序列之间的映射关系时，先要把总样本划分为两部分，即训练样本φ1和检测样本φ2：

φ1={(Pk,Tk)|P∈Rm,T∈Rn,

k=1,2,…,N1,N1≤N}

φ2={(Pk,Tk)|P∈Rm,T∈Rn,

k=N1+1,N1+2,…,N}

得到一个完善的映射关系需要两步：① 以训练样本φ1作为神经网络的学习数据并得到一个映射关系；② 以检测样本φ2为标准对得到的映射关系进行检测。若该网络对检查样本φ2中的输入数据能够得到较为准确的输出预测值，可认为此网络具有较好的泛化能力，具备实际应用价值；反之，则认为此网络不具备应用价值。

由于Mg/PTFE推进剂的配方因素和性能的数据之间存在很大差异(见表1)，最大数据与最小数据之间甚至相差上万倍，这种差异可能会对神经网络的训练造成不利影响。为了消除这种影响，在神经网络开始训练前，对网络的输入输出数据进行归一化处理。需要说明的是，表1中共有30组配方数据，选取前20组配方数据及其对应的燃速、燃烧温度和燃烧热数据作为训练样本，然后利用余下的10组数据进行预测试验，并将预测结果与其对应的试验结果进行比较验证。

3 预测结果分析与讨论

3.1 BP网络的预测结果

基于BP神经网络的基本原理，本文使用Matlab自带的神经网络工具箱函数建立了BP网络，采用表1中的前20组数据对网络进行学习，之后再对Mg/PTFE贫氧推进剂性能进行预测，并与后10组的实验值进行比较验证，预测结果如表2所示。

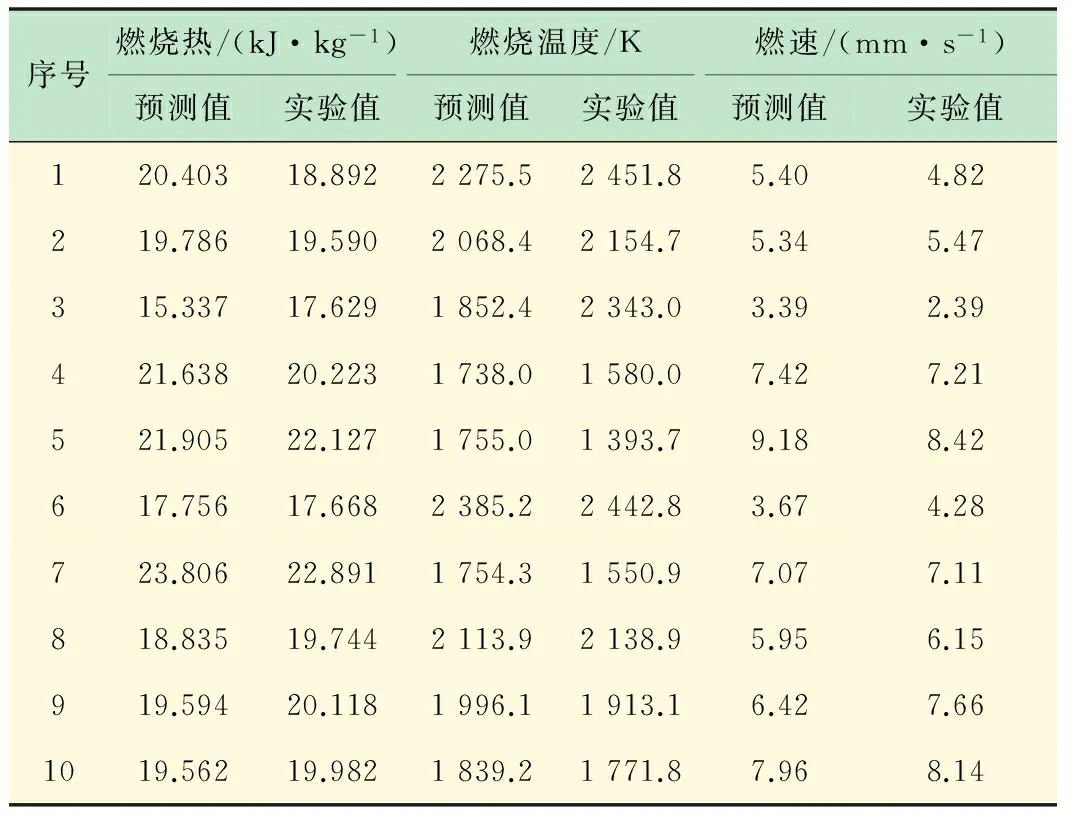
表2 BP网络预测值与实验值

3.2 SVM网络的预测结果

同理，采用SVM进行预测的相应结果见表3。

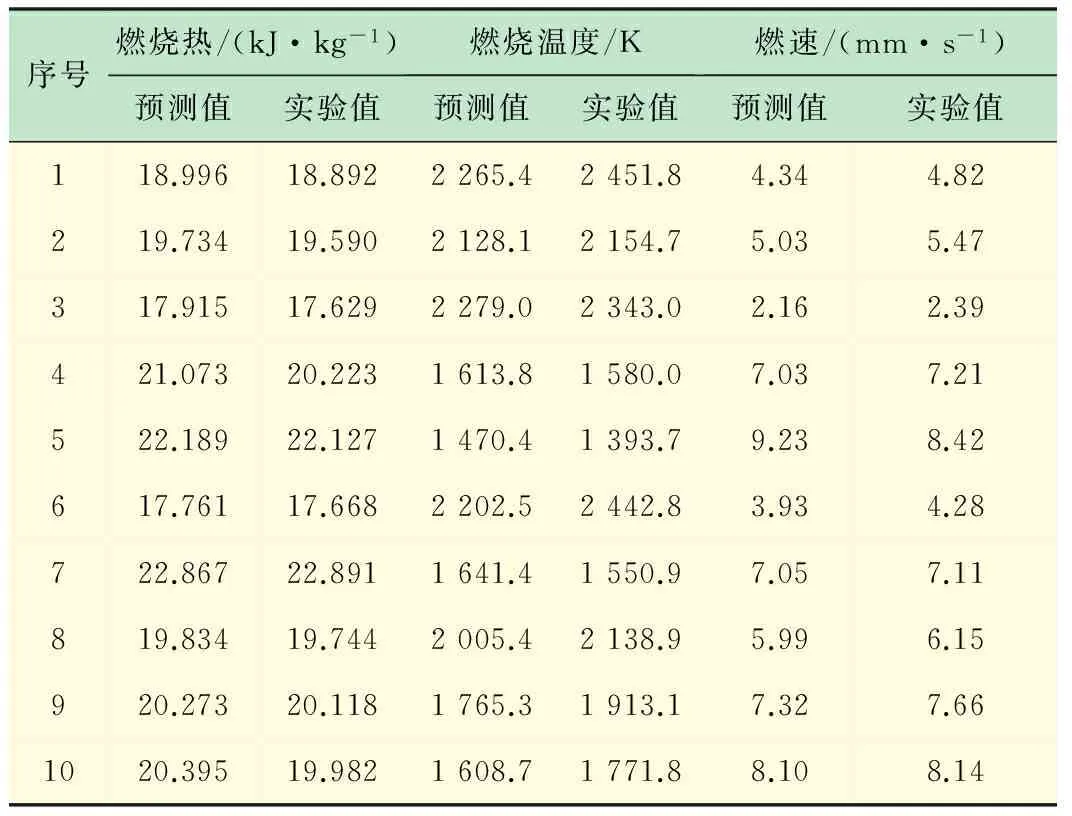
表3 SVM网络预测值与实验值

3.3 两种网络预测结果的比较

为了比较两种方法的预测性能的优劣，本文采用比较相对误差的方法来进行分析，其中燃烧热、燃烧温度和燃烧速度预测的相对误差分别如图3～5所示。

比较图3～5可知，对于燃烧热的预测而言，BP神经网络预测的最大相对误差为13.0%，而SVM预测的相对误差为4.2%；对于燃烧温度的预测而言，BP神经网络预测的最大相对误差为25.9%，而SVM预测的相对误差为9.8%；对于燃烧速度的预测而言，BP神经网络预测的最大相对误差高达41.8%，而SVM预测的相对误差为10.0%。因此可知，BP神经网络对Mg/PTFE贫氧推进剂性能预测的精度都较差，而且结果很不稳定，主要表现在图3～5中相对误差的起伏差距较大。分析其原因，主要由于BP网络对于训练样本量的要求较大。BP网络想要获得较好的泛化能力，其训练样本量要达到其连接权数量的10倍以上，以本文为例，输入层节点数为4，隐含层节点数为7，则样本量要达到7×4×10=280个，远远超过了本文的训练样本量(20组)，因此在本文中其预测的精度较差。

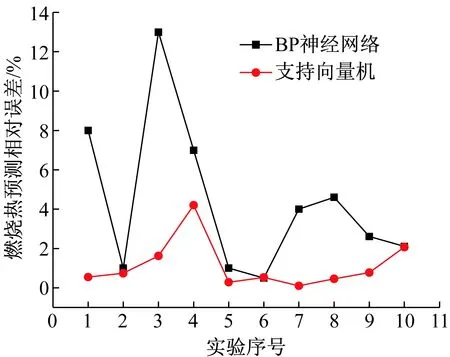
图3 SVM和BP网络对燃烧热预测的相对误差比较

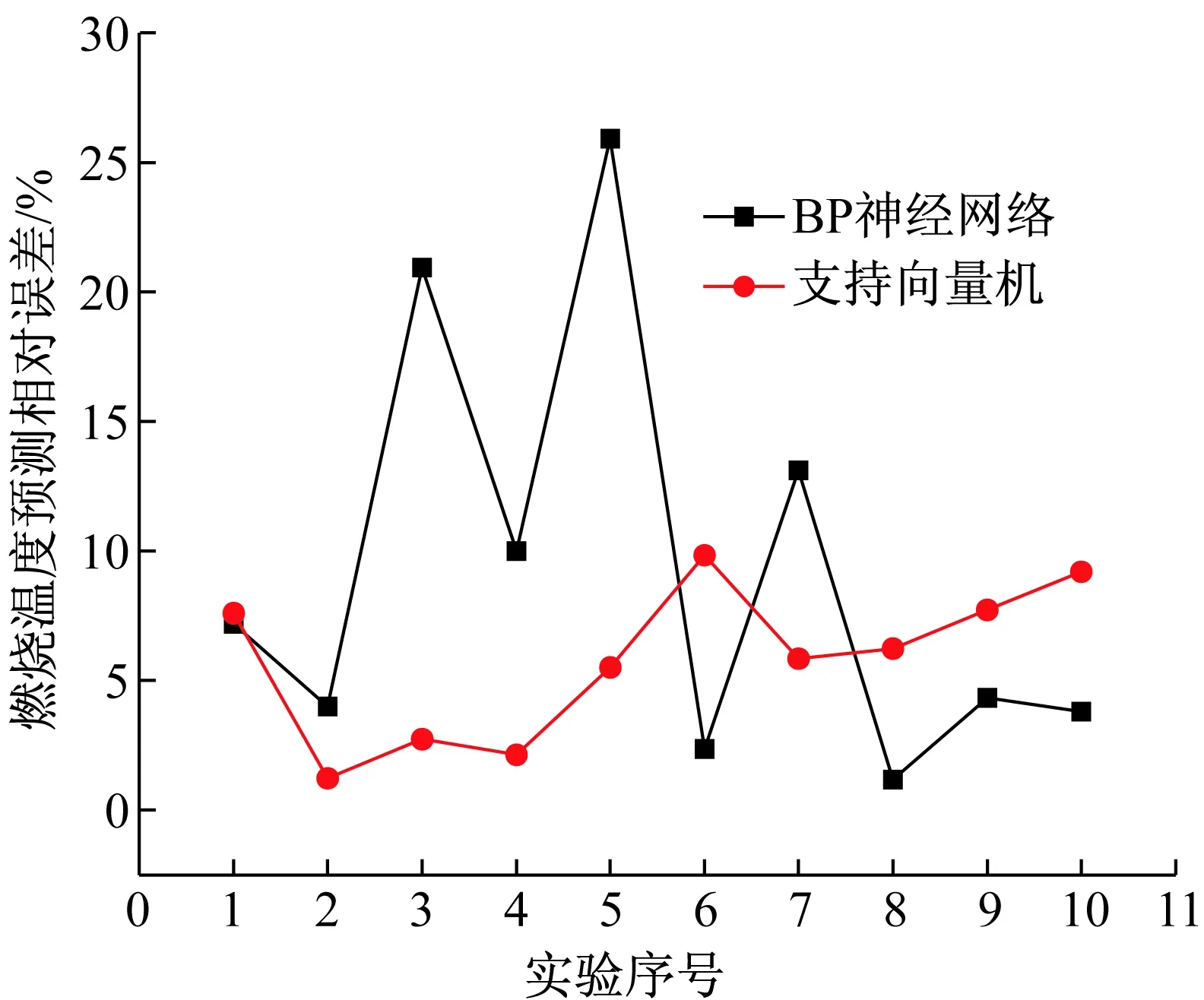
图4 SVM和BP神经网络对温度预测的相对误差比较

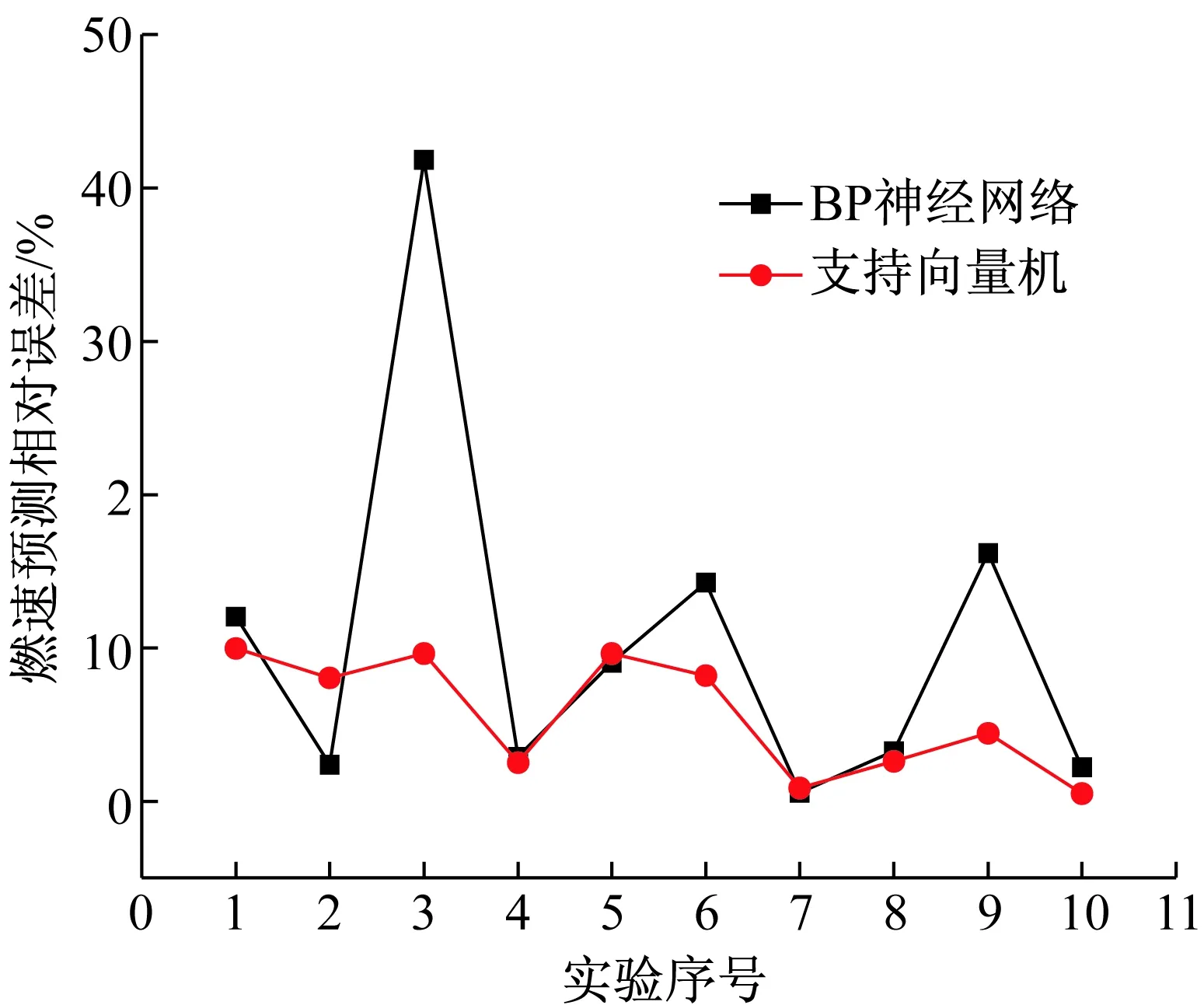
图5 SVM和BP神经网络对燃烧速度预测的相对误差比较

而SVM对Mg/PTFE贫氧推进剂性能的预测误差都较小，且保持在一个较好的水准。分析其原因主要是由于SVM不同于一般的采用经验风险最小化的神经网络(如BP神经网络)，它是采用结构风险最小化的原则，即将网络的训练误差作为优化问题的约束条件，以置信区间为优化目标，同时兼顾了其学习能力和泛化能力，而不像一般神经网络那样存在学习能力和泛化能力的矛盾，即出现所谓“过拟合”问题。因此相比较于其他神经网络，SVM具有更好的泛化能力。

4 结 语

本文分别使用BP和SVM对Mg/PTFE贫氧推进剂的性能数据进行了训练和预测，所得结论如下：① BP神经网络对训练样本量的要求比较高，需要大量的实验作支撑，用现有的20组数据训练时网络很不稳定且相对误差较大；② 比较发现，SVM网络在处理小样本量问题时具有其独特的优势，适合进行对Mg/PTFE贫氧推进剂性能预测的研究，相对误差较小。

[1] 潘功配, 杨 硕. 烟火学[M]. 北京：北京理工大学出版社, 2004.

[2] Ernst-Christian Koch. Metal-Fluorocarbon-Pyrolants: III. Develop-ment and application of magnesium/teflon/viton[J].Propellants,Explosives,Pyrotechnics,2002,27 (5):262-266.

[3] 郑 磊，潘功配，陈 昕，等．镁粉粒度对Mg/PTFE贫氧推进剂燃烧性能的影响[J]. 含能材料, 2010, 18(2): 180-183.

Zheng Lei, Pan Gong-pei, Chen Xin,etal. Effect of magnesium powder particle size on combustion properties of Mg/PTFE fuel-rich propellant[J]. Chinese Journal of Energetic Material, 2010, 18 (2): 180-183.

[4] Chen X, Zhao J, Pan G P,etal. Experimental study of PTFE powder size impact to Mg/PTFE pyrotechnic composition[J]. Advanced Materials Research, 2012, 463: 281-285.

[5] Williams M R, Dunne J L. Heat flux measurement from Bulk agnesium/Teflon/Viton (MTV) flare composition combustion[J]. Propellants, Explosives, Pyrotechnics, 2013, 38 (4): 563-568.

[6] Koch E C, Hahma A, Klapötke T M. Metal - Fluorocarbon pyrolants: XI. Radiometric performance of pyrolants based on magnesium, perfluorinated tetrazolates, and viton A[J]. Propellants, Explosives, Pyrotechnics, 2010, 35(3):248-253.

[7] Yong D E, Smit L V. A theoretical study of the combustion of magnesium/teflon/viton pyrotechnic compositions[R]. 1991, ADA243244.

[8] 许小平，张 唯．惩罚函数法计算燃烧产物的平衡组分[J]. 宇航学报, 1994, 6 (3): 90-95.

Xu Xiao-ping, Zhang Wei. Calculation of equilibrium composition of combustion products by penalty method[J]. Journal of Astronautics, 1994(3): 90-95.

[9] 王天放，李疏芬．最小自由能法求解 GAP在等压绝热条件下的燃烧产物[J].火炸药学报, 2003, 26 (4): 16-19.

Wang Tian-fang, Li Shu-fen. Free-energy minimization investigation on combustion of GAP under constant pressure and adiabatic condition[J]. Chinese Journal of Explosives & Propellants, 2003, 26(4): 16-19.

[10] 肖鹤鸣．高能化合物的结构和性质[M]. 北京：国防工业出版社, 2004.

[11] 徐丽娜. 神经网络控制[M]. 北京：人民交通出版社, 2000.

[12] Vladimir Cherkassky, Yunqian Ma. Practical selection of SVM parameteras and noise estimation for SVM regression[J]. Neural Networks, 2004, 17 (1): 113-126.

[13] 姚 潇, 余乐安. 模糊近似支持向量机模型及其在信用风险评估中的应用[J]. 系统工程理论与实践, 2012, 32 (3): 549-554.

YAO Xiao, YU Le-an. A fuzzy proximal support vector machine model and its application to credit risk analysis[J]. Systems Engineering—Theory & Practice, 2012, 32(3): 549-554.

[14] Jinbo Bi, Kristin P Bennett. A geomeetric approach to support vector regressin[J]. Neuro computing, 2003, 55 (1-2): 79-108.

[15] 刘国海, 张 懿, 魏海峰, 等. 多输入多输出非线性系统的最小二乘支持向量机广义逆控制[J]. 控制理论与应用, 2012, 29 (4): 492-496.

LIU Guo-hai, ZHANG Yi,WEI Hai-feng,etal. Least squares support vector machines generalized inverse control for a class of multi-input and multi-output nonlinear systems[J]. Control Theory & Applications, 2012, 29(4): 492-496.