关于初中数学“轻负担、高质量”的思考
2014-02-09王永斌
王永斌
(江苏省徐州市睢宁县凌城中学 徐州市 221233)
教育一直在呼唤为学生“减负”,即减轻负担,但在减负的同时又要求质量不能降低,这使很多教师陷入困惑,认为两者是不可能同时存在的。传统的教育理念使教师们达成了一种不成文的“共识”——要想质量高就必须要任务重,尤其是数学教学中,题海战术人们已经不再陌生并且也已经认可,但题海战术真的有效吗?“轻负担”与“高质量”两者真的是相互对立而无法相辅相成?在数学教学中两者真的无法达到平衡?新课改背景下认真思考“轻负担”与“高质量”在数学教学中的实际意义,是新时期赋予数学教育者最为重要的使命。笔者结合教学实例,对如何在数学教学中有效贯彻“轻负高质”理念进行了探究思考。
一、教给学生得当的方法,让他们“会学习”
数学教学过程存在两方面内容,一是教师应该怎样教,一是学生应该怎样学。随着新时期数学教师理念的不断更新,各种教育手段的不断优化与丰富,怎样教的问题已经初步解决,关键的就在于让学生怎样学,即如何让他们“学”的方法更得当,不但能够独立学习,更会独立学习。方法得当了,学生学生学习起来就会轻松很多,就会从心理上感觉负担轻了。如在教学生做题时,要让他们学会如何有选择性的进行练习,对于一看就会的可以先放放,确实不会的也不要空耗时间,可以先询问再做题,同时让学生养成建立“错题集”的习惯。做完题之后要及时引导学生对题型、结构、方法进行归纳与分析,通过变式训练让数学知识的外延与内涵得到充分彰显,甚至还可以让学生参与题目的改编。
如最为典型的“行程问题”:“A、B两站路程为480千米,慢车从A站出发,以60千米/小时的速度行驶,快车从B站以84千米/小时的速度行驶,两车相向行驶同时开车,几个小时后相遇?”这样的练习题稍加变化就可以形成多个不一样的问题:(1)如果快车先出发30分钟,慢车需要几个小时会与快车相遇?(2)两车相遇后慢车还需要几个小时才能够到达B站?(3)两车同向开出,快车在慢车之前,几个小时后两车之间的距离为600千米?这种变式练习,会让学生从机械化做题的“圈子”中跳出来,掌握到一种灵活的解题方法,会一题则会一“串”,如此举一反三,就会收到事半功倍的效果。
二、教会学生如何优化思路,让他们“学得快”
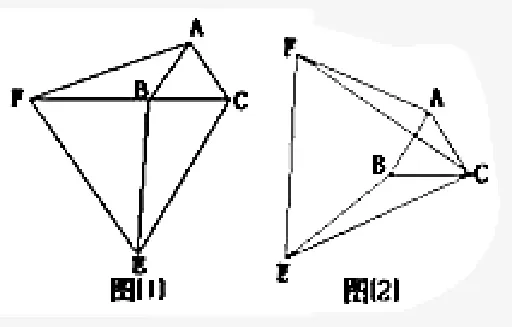
中学生在学会了如何学数学之后,怎样学得又快又扎实就成为了关键。在教师的帮助与指导下让学生们学会优化思路,不但能够提高学习效率,还对他们数学思维的良性发展有着十分积极的推进作用,这无疑是对“轻负高质”的有效落实。如对于相同的知识点可以对学生进行有效的归类训练,渐渐的他们就会对学习方法进行主动的归纳与积累,学会在知识的迁移中分析异同。如题:(1):图1中C点为两个大小不等的等边三角形ΔABC与ΔCEF的公共顶点,连接BF与AF,已知ΔAFC≌BEC,问BF与AF两者关系是怎样的?并证明结论。(2):如将图1中ΔCEF绕点C进行一定角度的旋转得到图2,题(1)中的结论是否成立?说明理由。(3)如将图1中ΔABC绕C点进行一定角度的旋转,会得以一个怎样的图形?(将图形画出)。你在题(1)中得到的结论是否仍旧成立?(4)通过以上三题的画图与求证过程,将你的结论进行归纳。上述一组题中主要是锻炼学生探究图形在运动变化中找到不变性质的能力,从题(1)中可以得出AF=CE;从题(2)中可心证明得结论仍旧成立;从题(3)的题意中可以画出多个符合条件的图形;从(4)中归纳结论:C点为不等大小的两个ΔABC和ΔCEF的唯一公共顶点,其中某个三角形绕C点进行任意角度旋转,都会得到“AF=BE”的结论。
三、平衡好“快节奏”与“大容量”两者关系
很多教师会将“轻负担、高质量”简单理解为为学生减少课下作业负担,但为了保证“高质量”却要“堤内损失堤外补”,在课堂上加大知识量,增加学习难度与密度,加快节奏,形成“快节奏、大容量”的教学现象。“快节奏”与“大容量”在教学中并非是不允许的,但容量的“大”表现在让学生的思维内容变得多起来,而不是一味增大知识量;而节奏的“快”是想办法让学生的思维活跃起来,但难度要保证与教材要求与学生实际认知水平保持一致。因此,教师可以借助教学辅助工具,如多媒体、演示实验等。
“轻负担、高质量”,并不是一味的削减学生的学习时间和学习内容,而是要教会学生同样的时间与内容如何用一种更简单而高效的方法去学习,从而让学习变得轻松而愉快。
[1]彭海泉.滴水可藏海,细节亦智慧——初中数学教学轻负高质的策略探微[J].科教文汇,2012,(33):113-114.
[2]刘亚萍.创建轻负高质的初中数学课堂[J].考试周刊,2014,(17):82-83.
