决策树在风险管理中的应用分析

2014-02-09张德江

重庆建筑 2014年5期

张德江

（重庆市建筑科学研究院，重庆 400020）

引言

一个企业在进行决策时，面对的风险纷繁复杂，若决策不当会给企业带来很大损失。因此，必须对面临的各种风险进行识别和分析，对各种方案进行比较和选择，正确决策，以最小风险的投入，获得可能的最大收益。当管理者面对的未来情况不止一种，而对未来最终可能会出现的结果又无法肯定，但却知道各种情况在各种自然状态下发生的概率时，就可采用决策树这一方法，进行对比分析，以作出最有利的决策。

1 决策树的原理

决策树(Decision Tree）又叫决策图，最早产生于上世纪60年代到70年代末，是直观运用概率分析的一种图解法，是一种在已知各种情况发生概率的基础上，利用风险收益分析，评价项目风险，判断其可行性的决策分析方法。其本质是通过一系列规则对数据进行分类的过程，是一种逼近离散函数值的方法，是数据挖掘分类算法中最直观的一种。

2 决策树的定义

决策树是一种通过图示罗列解题的有关步骤以及各步骤发生的条件与结果，从而作出决策的一种方法。该法将各种可行方案，可能出现的自然状态及其发生概率以及产生的后果（综合损益期望值）等诸多因素绘在同一张图上，然后对图中的各种方案在不同自然状态下的综合损益期望值进行计算，再比较各值的大小，最后选出较好方案，因其结构形如树枝，故称为决策树。

3 决策树的构成

决策树的构成有五个要素：决策点、方案枝、状态结点、概率分支和结果结点。

3.1 □——决策结点：是对几种可能方案分析选择后选择的最佳方案。用小方块□表示。

3.2 ○——状态结点：代表备选方案的经济效果（期望值），通过各状态节点的经济效果的对比，按照一定的决策标准就可以选出最佳方案。用小圆圈○表示。

3.3 方案枝：由决策结点引出到状态结点的若干条细支，每条细支代表一个方案，称为方案枝。用线段表示。

3.4 概率枝：由状态节点引出的分支称为概率枝，每条概率枝代表一种自然状态。在每条细枝上标明客观状态的内容和其出现概率。用线段表示。

3.5 △——结果节点：在概率枝的最末稍标明该方案在该自然状态下所达到的结果(收益值或损失值)。用小三角形△表示。

4 决策树的特点

4.1 优点

（1）生成的模式简单易于理解和实现。

（2）计算量相对来说不是很大。

（3）分类精度高。

（4）能够直接体现数据的特点，只要通过解释后都有能力去理解决策树所表达的意义。

（5）在相对短的时间内能够对大型数据源做出可行且效果良好的结果。

4.2 缺点

（1）对有时间顺序的数据，需要很多预处理的工作。

（2）当类别太多时，错误可能就会增加得比较快。

5 决策树的应用场合

决策树表达决策问题的方式形象生动，逻辑关系清晰明了，程序严谨，定量与定性分析相结合，能将问题各方面的逻辑关系条理化、简单化，便于研究、分析、修改、补充，方法简单，易于掌握。在企业管理实践中，经常会遇到这样的情景：若干个可行性方案制订出来了，企业内外部环境，大部分条件是已知的，但还存在一定的不确定因素。每个方案的执行都可能出现几种结果，各种结果的出现有一定的概率，存在着一定的胜算，也存在着一定的风险。这时，决策的标准只能是期望值。即，各种状态下的加权平均值。针对上述问题，用决策树法来解决则不失为一种好的选择。在企业的投资决策之中，它是随机决策模型中最常见、最普及的一种决策模式和方法，能有效地控制决策带来的风险，适用于在比较复杂的情况下进行决策。

决策树法属于风险型决策方法，不同于确定型决策方法，二者适用的条件也不同。应用决策树决策方法必须具备以下条件：

（1）具有期望达到的明确目标。

（2）存在可以选择的两个以上的可行备选方案。

（3）存在着决策者无法控制的两种以上的自然状态(如气候变化、市场行情、经济发展动向等)。

（4）不同行动方案在不同自然状态下的收益值或损失值(简称损益值)可以计算出来。

（5）决策者能估计出不同的自然状态发生概率。

6 决策树的应用步骤

6.1 绘制决策图

（1）首先绘出决策点，即决策树的始点，用符号□表示。

（2）由决策点开始，自左向右展开，用直线段引出若干方案枝，每条方案枝代表一个可行性方案，在其线段上方标明其方案内容。

（3）在各方案枝末端用符号○表示方案状态结点。

（4）从各方案状态结点用直线段引出若干概率分支，每条概率分枝代表一种自然状态，在其线段上方标明该自然状态发生的概率P。

（5）在各概率分枝末端标出结果结点，用符号△表示，将该状态下的损益值q标在△右侧。

6.2 分析-比较-决策

（1）由右向左逐步后退进行分析、计算各种状态下的综合损益期望值，将其结果标注在○上方。

某方案的综合损益期望值q=∑ （方案在某种自然状态下发生的概率×该自然状态下的损益值）。

（2）比较不同方案的综合损益期望值，选出合理的决策方案，两害相权取其轻，两利相权取其重，最后确定选定的方案，标注在□上方；未被选用的方案则用两平行短线截断，称为“剪枝”。

6.3 对方案的优劣及可靠性进行评价（一般用于两个方案的情况）

表1 经营安全状况比较

方法三：计算各方案在为低于转折概率p的某个概率Pd时（一般可取Pd=（0.8～0.9）p）,其综合损益期望值的变化率Kd，Kd大的方案可靠性较差。

7 案例

例题1：决策树法在施工管理决策中的应用之一

某建设工程需要特种水泥用于防水工程，又需特种钢材用于钢结构工程。但两种材料的供应都很紧张，受运输等条件限制，施工时只能保证一种材料得到供应。若水泥供应得到保证，则防水工程将投资30万元，否则将亏损10万元。若钢材供应得到保证，则钢结构工程投资为50万元，否则将亏损25万元。而水泥供应的保证率为0.4，钢材供应的保证率为0.6。问该优先保障水泥供应或保障钢材供应？

解：

第一步：绘制决策树如下。

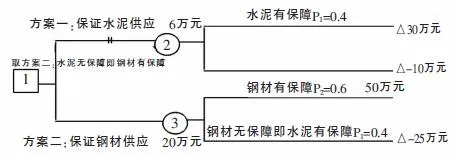
第二步：由右向左逐步后退进行分析、计算各方案的综合损益期望值q并将结果标在点②、③之上。

点②：q1=30×0.4+(-10)×(1-0.4)=6(万元)

点③：q2=50×0.6+(-25)×(1-0.6)=20(万元)

第三步：比较决策。

因为q2＞q1，所以决策点取q2=20万元，即采用保障钢材供应的方案，将结果标在□上。并用两平行短线将方案一切断。

第四步：进一步对方案的优劣及可靠性进行评价。

因为P2=0.6 即P2＞，所以保障钢材供应的方案较优。

方法二：计算决策安全率K

此K值较大，查表可知：选择保障钢材供应的决策方案，经营较安全。

方法三：比较各方案保证概率低于转折概率时，其综合损益期望值变化率Kd

计算各方案在钢材保证率下降为0.430434时的综合损益期望值变化率Kd

说明当钢材供应保证率低于转折概率时，其综合损益期望值的变化率比水泥的相应变化率小得多，即钢材供应保证率的变化对工程的影响不大，所以该方案的可靠性较高，这与前面的分析结果基本一致。

结论：应采用保障钢材供应的方案。

例题2：决策树法在施工管理决策中的应用之二

有一项工程，施工管理人员需要决定下月是否开工。如果开工后天气好，则可为国家创收8万元；若开工后天气坏，将给国家造成损失2万元；不开工则损失2000元。根据过去的统计资料，下月天气好的概率是0.3,天气坏的概率是0.7。请做出决策。

解：

第一步：绘制决策树如下。

第二步：由右向左逐步后退进行分析、计算各方案的综合损益期望值q并将结果标在点②、③之上。

点②：q1=8.0×0.3+(-0.2)×0.7=2.26(万元)

点③：q2=(-0.2 ×0.3+(-0.2)×0.7=-0.74(万元)

第三步：比较决策。

因为q1＞q2，所以决策点取q1=2.26万元，即采用开工的方案，将结果标在□上。并用两平行短线将方案二切断。

第四步：进一步对方案的优劣及可靠性进行评价。

因为P1=0.3 即P1＞，所以开工的方案较优。

方法二：计算决策安全率K

此K值较大，查表可知：选择开工的决策方案，经营安全。

方法三：比较各方案保证概率低于转折概率时，其综合损益期望值变化率Kd

计算各方案在天气好保证率下降为0.162时的综合损益期望值变化率Kd

说明当天气好保证率低于转折概率时，其综合损益期望值的变化率比天气坏的相应变化率小得多，即天气好保证率的变化对工程的影响不大，所以该方案的可靠性较高，这与前面的分析结果基本一致。

结论：应采用开工的方案。

例题3：决策树法在投标决策中的应用

某建筑公司打算参加甲、乙两项工程的投标。因受本单位资源条件限制，只能选择其中一项工程投标。根据过去类似工程投标的经验数据，甲工程投高标的中标概率为0.3,投低标的中标概率为0.8,编制该工程投标文件的费用为5万元；乙工程投高标的中标概率为0.5,投低标的中标概率为0.6，编制该工程投标文件的费用为3万元。各方案承包的效果、概率、损益值如表2所示。问如何确定投标方案？