基于排队理论的充电站最优配置

林 琳，高亚静

(华北电力大学 电气与电子工程学院，河北 保定 071003)

基于排队理论的充电站最优配置

林 琳，高亚静

(华北电力大学 电气与电子工程学院，河北 保定 071003)

在分析电动汽车充电行为的基础上，利用MATLAB建立了充电服务系统的排队模型，仿真的目的在于寻求顾客与充电站服务设置之间的平衡点，保证充电站具有最佳的服务效率和最合理的配置。根据统计规律得出相关参数，最后综合考虑充电站的投资费用、充电装置的闲置率及顾客的满意度等因素，进而得出充电站为满足一定的服务水平应该设置的充电装置个数。研究结果表明，通过合理配置充电设施数量，可以提高充电站的服务效率以及设备的综合利用率，从而进一步验证了模型的有效性。

电动汽车;排队论;充电装置;最优配置;MATLAB

0 引言

电动汽车是一种发展前景广阔的绿色交通工具，是解决能源以及环境问题［1］的重要手段。现如今，电动汽车的相关技术已经成为国内外众多学者研究的热点，作为电动汽车推广应用的前提和基础，充电装置的规划和建设也逐步引起了人们的关注［2］。电动汽车充电站是电动汽车能量补给的重要基础支撑系统，同时也是电动汽车商业化、产业化过程中的重要环节，随着充电设施的大规模建设，科学合理的配置电动汽车充电设施显然已成为当前急需解决的问题之一。目前，电动汽车充电设施的研究已经取得了显著的成果［3～6］，大部分已经发表的文献主要关注电动汽车充电站的规划建设问题，而本文基于对电动汽车充电行为的分析，在MATLAB上建立充电设施服务系统的排队模型，研究了充电设施服务系统在排队等候中的特征，目的是要寻找充电对象与充电服务设施之间的最佳配置，保证充电站系统具有最佳的服务效率与最合理的配置，从而提高充电站的综合利用率。

1 电动汽车充电站排队问题分析

1.1 充电站排队论的基本原理

排队论［7］的主要元素包括两个方面:一是需要接受服务的顾客;二是提供服务的服务台数量。在充电站排队系统中，顾客希望排队等待的时间越短越好，这就需要充电站设置较多的充电装置，从而减少排队的等待时间，但是这样会增加充电站的运营成本，对充电站投资者造成很大压力;若充电装置过少，排队等待的时间就会增加，服务质量则会降低。因此，如何权衡两者之间的关系，寻求最佳的充电装置数量就显得尤为重要。

充电站排队理论［8］通过对顾客到达时间和服务时间的统计分析，得出等待时间、排队长度、充电装置闲置率等统计量指标，根据得出的指标参数进而改进服务系统的结构，使得服务系统既可以满足顾客的需求，又能够使系统的某些指标得到优化。

1.2 电动汽车充电站服务排队模型

每辆电动汽车到达充电站接受充电服务都是相互独立的，其特点具有平稳性、无后效性及普通性。充电站服务是一个随机服务系统，该系统具有以下特征:被服务的对象是已经排好队准备接受充电服务的顾客，顾客源是无限的，顾客之间相互独立，顾客相继到达的时间间隔是随机的。系统有多个充电装置且对每个顾客充电的服务时间是相互独立的。其服务规则遵从先到先服务(FCFS)的原则，即某一电动汽车到达充电站时，如果充电装置有空闲，则可以接受充电服务，当服务结束以后就离开充电站;如果充电装置没有空闲，则电动汽车需要排队等待服务，直到充电站有空闲的充电装置时再按照一定的顺序接受充电服务。每个充电装置前都有排队队列，顾客按照意愿选择队列排队等候，这样形成多充电装置(M/M/C)的排队系统。充电站顾客排队系统结构见图1。

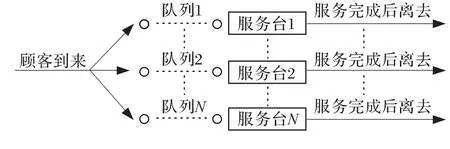
图1 多服务台排队系统图

1.3 排队问题的数学模型

1.3.1 随机变量数值序列

研究表明，电动汽车的充电行为具有较大的随机性和灵活性，通过对电动汽车所处情况的多样性以及电动汽车运行条件的各种不确定影响因素的分析，可知到达充电站的电动汽车数量随时间变化的规律［9］服从参数为λ的泊松分布，设随机变量X(单位时间内顾客到达数)，满足泊松分布X=P(λ)，概率分布为:

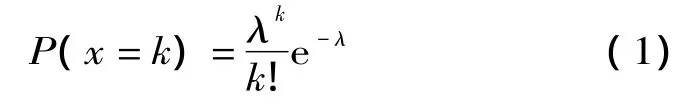
到达时间间隔和服务时间均服从负指数分布，设随机变量T(顾客相继到达间隔时间)满足负指数分布，即

随机变量V(顾客相继离开的间隔时间)，满足负指数分布，即

式中:u1，u2为 (0，1)区间上独立、均匀分布的随机变量。

1.3.2 充电站排队系统的运行指标

根据统计数据得到的单位时间内到达站内接受服务的顾客数量和每位顾客接受服务的时间，通过χ2拟合检验，得到单位时间内顾客到达充电站内的数量服从Poisson分布，设平均每小时到达λ辆;从前面介绍已知电动汽车快速充电时间服从负指数分布，设平均充电时间为u。根据已知条件，设电动汽车排队系统在时刻t有n辆电动汽车等候，此时系统的状态为n，同时，记系统在时刻t状态为n的概率为Pn(t)，它决定了系统运行的特征。其状态瞬时强度转移图如图2所示。

图2 状态转移图

由状态转移关系得到电动汽车充电装置服务系统的稳态方程:

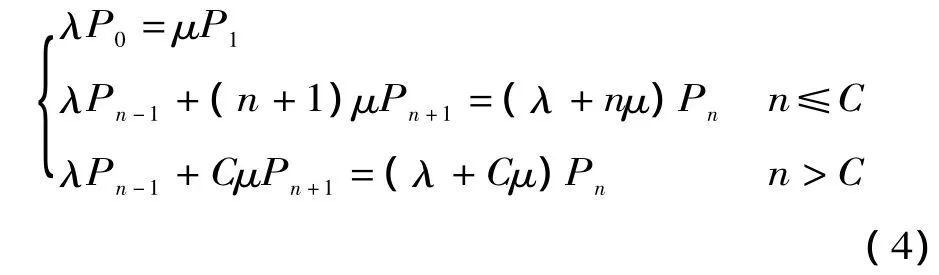
式中:Pn为n辆电动汽车能够接受充电服务的概率;C为充电站内能够提供充电服务的充电装置数量;n为接受充电服务的电动汽车的数量;当0≤n≤C时，表示充电站内有n辆电动汽车正在接受充电服务，其余C－nC－n个可充电装置处于空闲状态;当n＞C时，表示充电站内C个充电装置全部处在忙碌状态，其余n－C辆电动汽车排队等候充电。

采用递推法求解式 (4)的差分方程，得到充电站内车辆接受充电的概率为:

由此得到充电站内排队系统的运行指标如下:

(1)充电站设施利用率ρ为:

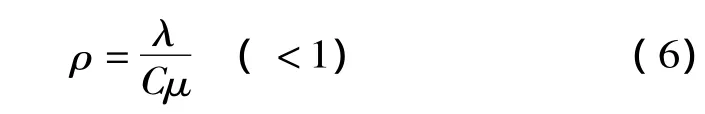
当ρ≤1时，不会排成无限队列，充电站内平均到达率等于离去率，达到平衡状态;当ρ＞1时，就会出现排队现象，即顾客排队等待。

(2)充电站内充电装置的闲置率:

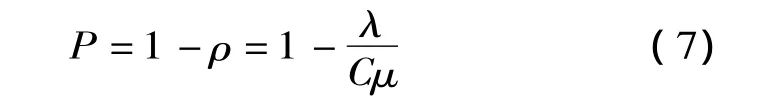
(3)充电站内平均排队等待队长lq为:

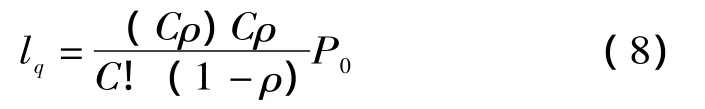
(4)充电站内平均队长l为:

(5)充电站内车辆的平均排队时间Wq为:

(6)充电站内车辆的逗留时间W为:

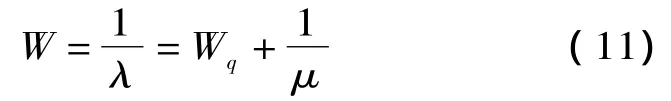
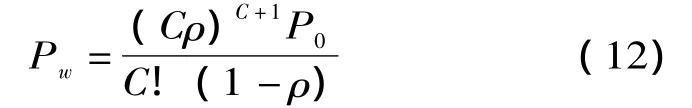
(8)对于需要接受充电服务的顾客来说，充电站内的平均队长越长，顾客需要等待的时间就越长，顾客必须等待的概率就越大，因此定义顾客满意度为:

(7)电动汽车进入充电站内需要等待的概率

(9)充电站内充电功率负荷限制

由电动汽车在充电站内接受充电的概率可假设，在一段指定时间内接受充电的电动汽车数量为n辆，n辆电动汽车的充电行为相互之间是独立的，从而n辆电动汽车之中需要进行充电的数量X服从参数n，p的二项分布，记作X～B(n，p)。本文将每个时间段内充电行为视为一个负荷需求点，需要进行充电的电动汽车数量的数学期望E(X)视为充电功率。则有

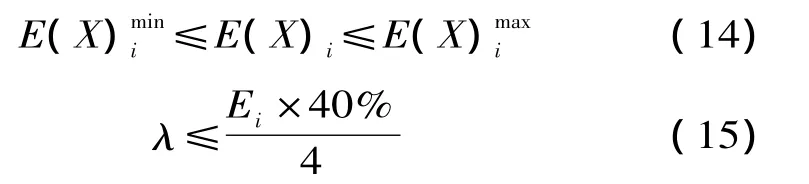
其中，i表示第i个时间段。

(10)充电站内充电装置台数最优配置模型

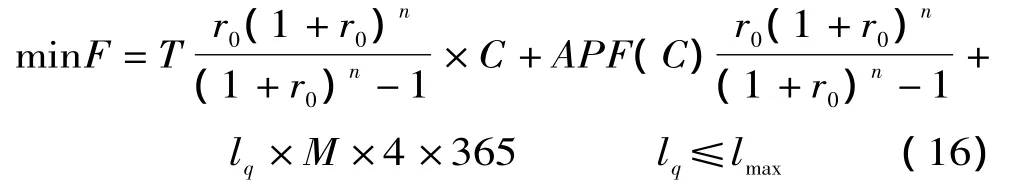
式中:F为充电站年消耗费用;T为单个充电装置费用;C为最优充电装置数目;M为顾客的出行时间价值;APF(C)为C台充电装置需要谐波等治理的投资费用;r0为折旧率;n为充电装置的折旧年限;lq为平均排队长;lmax为充电站内所能接受的最大充电排队队长。

因为C只能取整数，采用边际分析法，根据F是最小的特点，得到:

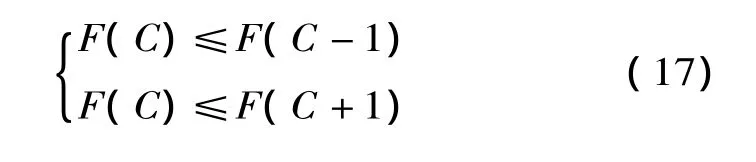
2 充电站内仿真系统模拟

2.1 仿真程序设计过程

假设顾客源是无限的，顾客的到达是相互独立的，顾客按照规定的到达模式到达充电站内，同时按照规定的服务方式产生服务时间。顾客进入充电站后，首先判断是否有空闲的充电装置，若有，则直接接受服务而不需要排队等待，否则，顾客将排队等待服务。仿真的过程以顾客到达为驱动，一个顾客到达站内后，按照仿真流程计算其服务时间及离开时间，前一个事件完成后开始驱动下一个事件进行。在仿真过程中，还要统计各服务台的利用率、队列长度、顾客的等待时间以达到仿真的目的。

电动汽车充电站与人们日常生活行为息息相关，其进站分布时间与加油站车辆相似，集中的加油或充电时间将导致拥挤排队现象，削减顾客的使用率，而过多充裕的充电装置则会使得投资成本增加，依据加油站统计资料［10］显示，约4成加油行为发生在16∶00～20∶00。电动汽车到达充电站后寻求空闲的充电装置为其服务，借鉴汽车加油站统计方法及充电行为规律，得出如下参数:假设运营时间为5∶00～23∶00，其日充电次数可达200～300次，各时段到达车辆如表1。

表1 各时段到达车辆

建立的模型以加油站16∶00～20∶00的充电行为为例，到达充电站的泊松流参数为24.46，设充电机的充电时间为30 min，则μ=2，即每台充电装置平均每小时可为2台电动汽车进行快充服务，顾客的出行价值为20元/h［11］，每台充电机的投资为3万元，电动汽车充电站APF装置依据装置选择表［12］选择容量为120 kVA的两台配置，折旧率为0.1，回收年限为20年。基于MATLAB程序［13］的模拟动态仿真流程图如图3。

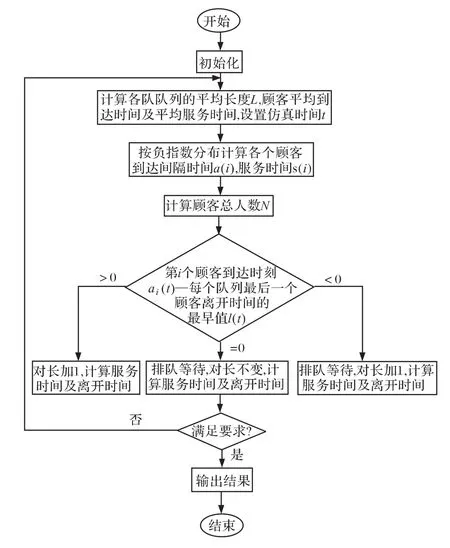
图3 MATLAB动态仿真流程图

2.2 仿真结果与分析

根据MATLAB仿真程序得到的动态仿真模拟结果如表2所示。

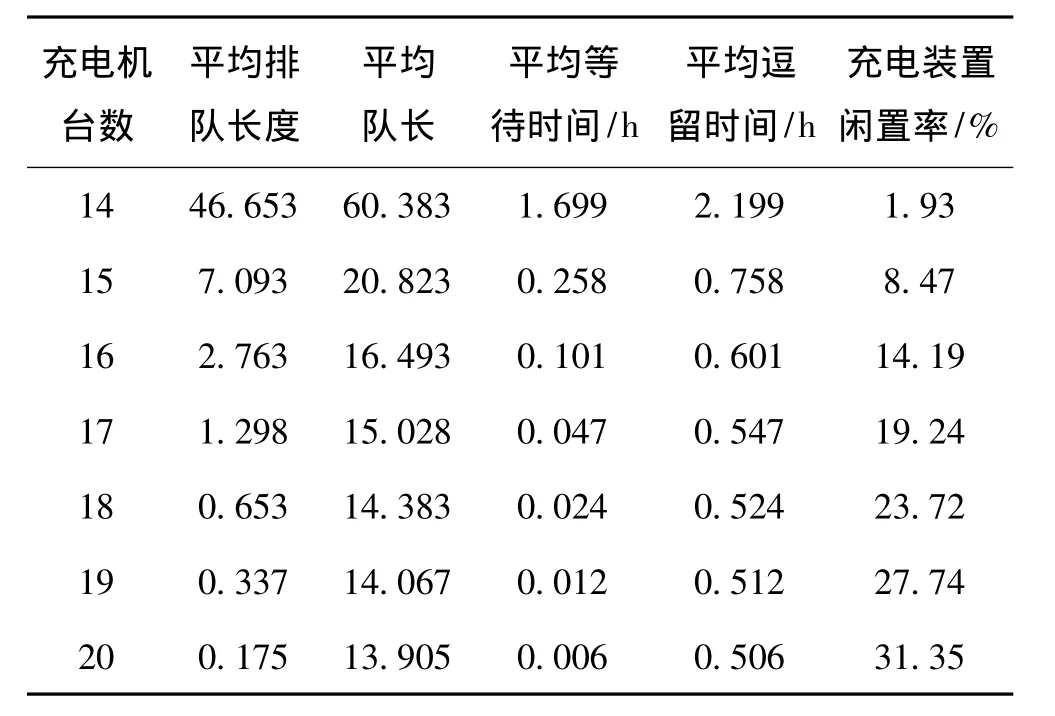
表2 动态仿真模拟结果

由表2中数据可以得出，在顾客到达为24.46人/h，服务强度2辆/h的情况下，充电站内配置14台充电装置时，充电装置几乎没有空闲，顾客的等待时间超过1 h;而配置20台充电装置时，顾客几乎不用等待，充电装置闲置率超过30%;综合考虑充电站年消耗费用、电源点负荷、顾客等待概率及顾客的满意度，根据公式 (13)～(17)得出充电站内充电装置最优配置台数为16台，此时充电装置服务强度为0.858，平均每个顾客需要等待的概率为0.427，等待时间为6 min，顾客满意度为0.14，这种情况下能够兼顾投资者和顾客的双方利益，使投资者和顾客都比较满意。本文在分析过程中只是假设在具体时间段寻求充电站内充电装置的最优配置台数，根据相类似的方法可以针对不同时间段充电的顾客数量和服务强度的变化进行动态仿真，得到不同情况下充电站内应该配置多少个充电装置才能最优，这样可以根据随时动态变化的客流，提高客流的服务量及顾客的满意度。

3 结论

本文基于排队理论分析了充电站内最优充电配置的问题，充电站内的充电装置的选择兼顾充电站与顾客双方的利益，以充电站的服务成本、充电装置的闲置率及顾客的满意度为综合考虑因素，基于排队论理论分析，通过编写MATLAB程序得出最后结果，验证了该模型的有效性。经过分析可以看出，充电站内充电装置的合理配置，不仅可以为顾客提供较为优质的服务，而且可以使得充电站的配置资源得到很好地利用。最优配置问题的解决，为今后充电站的定容选址和规划发展都提供了一定的理论依据，本文中对于与充电站相关联的电能质量影响相关因素没有充分考虑，这些都将在以后的工作中进行更加详细的分析和研究。

［1］张文亮，武斌，李武峰，等．我国纯电动汽车的发展方向及能源供给模式的探讨 ［J］．电网技术，2009，33(4):1-5．

［2］熊虎，向铁元，荣欣，等．电动汽车电池更换站布局的最优规划 ［J］．电力自动化设备，2012，32(9):1-6．

［3］杨永标，丁孝华，朱金大，等．物联网应用于电动汽车充电设施的设想 ［J］．电力系统自动化，2010，34(21):95-98．

［4］赵俊华，文福拴，薛禹胜，等．计及电动汽车和风电出力不确定性的随机经济调度 ［J］．电力系统自动化，2010，34(20):22-29．

［5］黄梅，黄少芳．电动汽车充电站谐波的工程计算方法［J］．电网技术，2008，32(20):20-23．

［6］滕乐天，何维国，杜成刚，等．电动汽车能源供给模式及其对电网运营的影响 ［J］．华东电力，2009，37(10):1675-1677．

［7］唐应辉．排队论［M］．北京:科学出版社，2006．

［8］吴飞．产生随机数的几种方法及应用 ［J］．数值计算与计算机应用，2006，27(1):48-51．

［9］韩中庚．实用运筹学模型、方法与计算 ［M］．北京:清华大学出版社，2007．

［10］沈丽娜．城市加油站空间布局优化研究 ［D］．青岛:中国海洋大学，2010．

［11］齐彤岩，刘冬梅，刘莹．北京市居民出行时间成本研究 ［J］．公路交通科技，2008，25(6):144-146．

［12］尹国龙．电动汽车充电设备电能质量分析及改善研究［D］．北京:华北电力大学，2011．

［13］黄永安，马路，刘慧敏．Matlab 7.0建模仿真开发与高级工程应用［M］．北京:清华大学出版社，2007．

Charging Stations Optimal Allocation Based on Queuing Theory

Lin Lin，Gao Yajing

(School of Electrical and Electronic Engineering，North China Electric Power University，Baoding 071003，China)

Based on the analysis of electric vehicle charging behavior，a system of charging infrastructure service queuing model is established using MATLAB software．The simulation purpose is to seek the best configuration settings between customer service and the charging station，to ensure optimum charging station service efficiency and the most reasonable configuration．The relevant parameters are obtained according to statistical rules．Finally，the number of the charging device in the charging station to meet a certain level of service is got by considering customer satisfaction and charging station investment costs．The results show that rational allocation of charging infrastructure in the charging station can improve service efficiency and equipment utilization rate，which further proves the validity of the presented model．

electric vehicles;queuing theory;charging device;optimal allocation;MATLAB

TM912

A

10.3969/j.issn.1672-0792.2014.04.008

2013－09－29。

林琳 (1988-)女，硕士研究生，研究方向为电力系统分析与控制，E-mail:844561731@qq．com。