基于PMU数据的输电线路参数跟踪估计

常鲜戎，崔赵俊，张海生

(华北电力大学 电气与电子工程学院，河北 保定 0 71003)

基于PMU数据的输电线路参数跟踪估计

常鲜戎，崔赵俊，张海生

(华北电力大学 电气与电子工程学院，河北 保定 0 71003)

输电线路参数的准确估计直接影响着电力系统建模、稳定计算及运行控制。同步相量技术的出现为输电线路参数在线辨识提供了有力条件。针对离线求取输电线路参数的局限性，借助PMU实测数据，对电力系统中的单条输电线路参数进行辨识，并采用可变遗忘因子的最小二乘法辨识线路参数，提出采用增量灵敏度分析系统运行工况变化对参数辨识结果影响的思路。某实际电网中的500 kV输电线路仿真结果验证了此方法的可行性。

输电线路;参数估计;最小二乘法;数据窗口;增量灵敏度

0 引言

随着电力系统互联规模的不断扩大、电力需求的迅猛增长和新型能源电源的接入，电力系统运行方式越来越复杂多变，使得大型互联电网的实时稳定监控及智能化建设变得愈发困难。准确的电网参数是建立精确系统模型，并对电网进行分析计算的基础。因此，提高电力系统参数的准确性和可靠性，尤其是输电线路参数的准确性，对大型互联电网的安全稳定运行具有重要意义［1～6］。

离线求取输电线路参数的计算方法主要有:理论计算法［7］、参数实测法［8］。传统离线辨识的参数由于精度不高逐渐不能满足要求，实时估计输电线路参数变得更加迫切。广域测量系统(WAMS)作为在线获取电网广域动态信息的重要途径，为在线估计输电线路模型参数提供了重要保障［9～11］。

本文借助PMU实测数据，对多机系统中输电线路进行建模，采用具有可变遗忘因子的改进最小二乘法 (regularized robust recursive least squares with variable forgetting factor，VFFR3LS)［12］在线辨识输电线路参数;提出采用增量灵敏度分析负荷变动对输电线路参数辨识的影响。

1 输电线路参数估计模型

电力系统建模和分析计算中，输电线路模型通常采用Π型等值电路［13］，如图1所示。

图1 输电线路等值模型

图1中，线路各参数均为相量，其中I1=I1∠θ1，I2=I2∠θ2，U1=U1∠δ1，U2=U2∠δ2，1/Z=g+jb，YB=jB，忽略电导。若线路两端均配有PMU测量装置，可得到实时测量的电压和电流相量，则k时刻线路两端的电压电流关系为

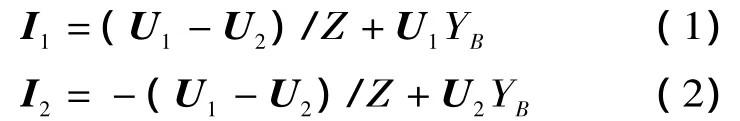
分离实部、虚部，推导得到k时刻输电线路参数求解方程如式 (3)所示。式 (3)为一个线性方程组，利用线性方程组的求解方法即可得出k时刻输电线路参数辨识结果。

为了提高辨识结果的精度，可假设在一个数据窗中，输电线路参数不变，通过合理设定数据窗的长度来改善参数辨识效果。

2 参数辨识方法

PMU测量数据不可避免的存在误差，而最小二乘法作为一种非统计学的参数估计方法，在随机环境中，并不需要知道测量数据的概率统计信息，但获得的估计结果却有较好的统计性质，因而具有较好的容差能力［14～15］。因此，本文采用可变遗忘因子的最小二乘方法来在线辨识输电线路参数。

假设向量θ是未知参数向量，为确定估计误差准则，构造一个线性模型如下:时刻k的估计误差定义为

具有一定的鲁棒性，一般情况下可定义为:

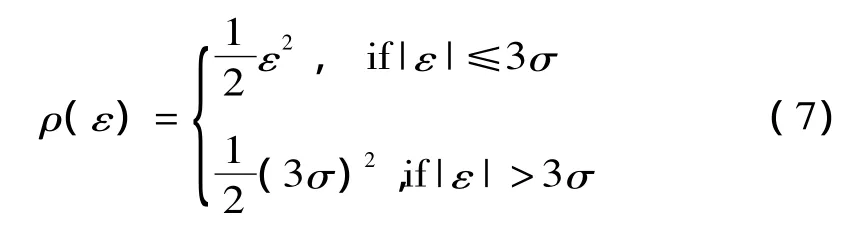
式中:σ为ε的标准偏差。

θ的具有遗忘因子的正规化最小二乘估计为:

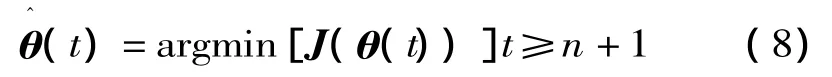
本文针对R3LS算法中遗忘因子始终不变的缺陷，采用可实时跟踪电网状态变化的可变遗忘因子，即:

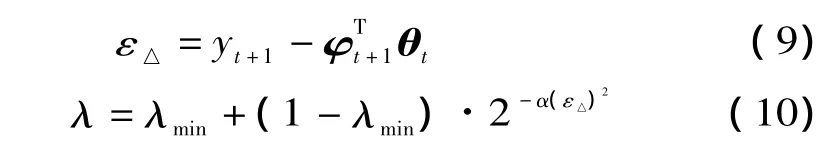
式中:α为敏感系数，反映了遗忘因子趋近于1的速率;估计误差ε△可实时跟踪电力系统的运行状况。

3 算例分析

本文以某地区电网中实际运行线路为例对所提方法进行验证。首先在PSASP中建立系统模型，模拟电网实际运行状况，同时设定全网负荷缓慢增长 (有功负荷的增长速率为初始有功负荷的10%/s，无功负荷的增长速率为初始无功负荷的3.19%/s)，使研究线路上流通功率缓慢增加，并在Visual C++6.0中编程实现输电线路参数实时辨识。系统中给定某500 kV线路参数设定值为R=0.025 2，X=0.197 8，B=0.114 7(注:线路参数均采用标幺值，系统基准功率为SB=1 000 MVA，电压基准为UB=525 kV)。

3.1 量测数据模拟

设定线路两侧均配备PMU装置，可同时监测线路两端节点的电压、电流相量。表1给出了6组线路两端电压、电流数据实时量测的真实值。

表1中，给出了0～100周波，线路两端的PMU量测数据，由于电力系统正常运行状态下处于各种小扰动中，加之PMU测量装置的采样间隔较小，因此，输电线路上的电流变化不会很大。从线路两端电压幅值来看，随着系统负荷不断增长，线路两端电压幅值逐渐下降，但下降的幅度相对不大;从线路两端电压相角来看，线路末端电压相角超前于始端电压，说明线路电流由末端流向始端。从线路电流幅值来看，随着时间推移，电流幅值逐渐增大，说明线路上流通功率逐渐增加。从线路电流相角来看，线路两端电流的相角差变化不大。

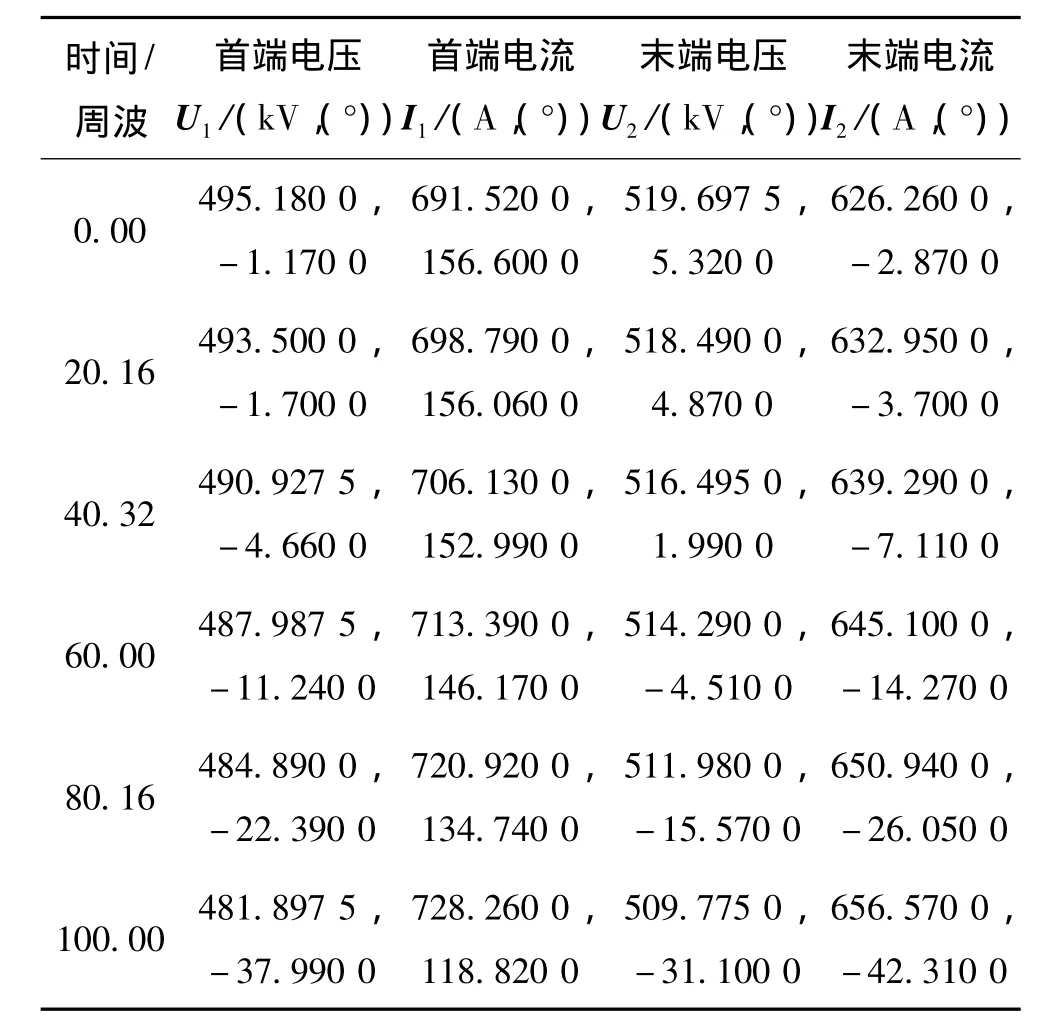
表1 线路两端PMU测量数据

在PMU量测数据的基础上，加入高斯白噪声。假设所有数据的测量误差均值为0;电压和电流的幅值标准差为0.6%，相角标准差为0.8%。采用编程的方法得到量测量的随机误差，叠加真值形成带误差的PMU测量数据。图2给出了节点电压和电流幅值测量误差。

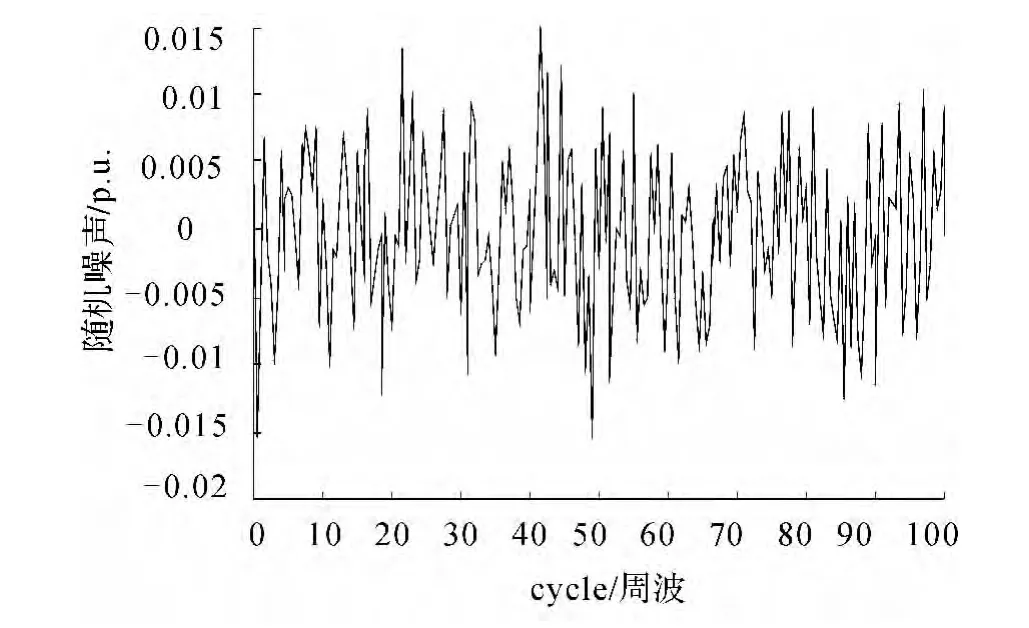
图2 节点电压和电流测量误差

3.2 输电线路参数计算

依据最小二乘法，采用式 (3)、(8)可计算得到单次测量数据计算的线路辨识参数，如图3所示。其中:曲线1代表传统RLS算法计算结果;曲线2代表R3LS算法计算结果。

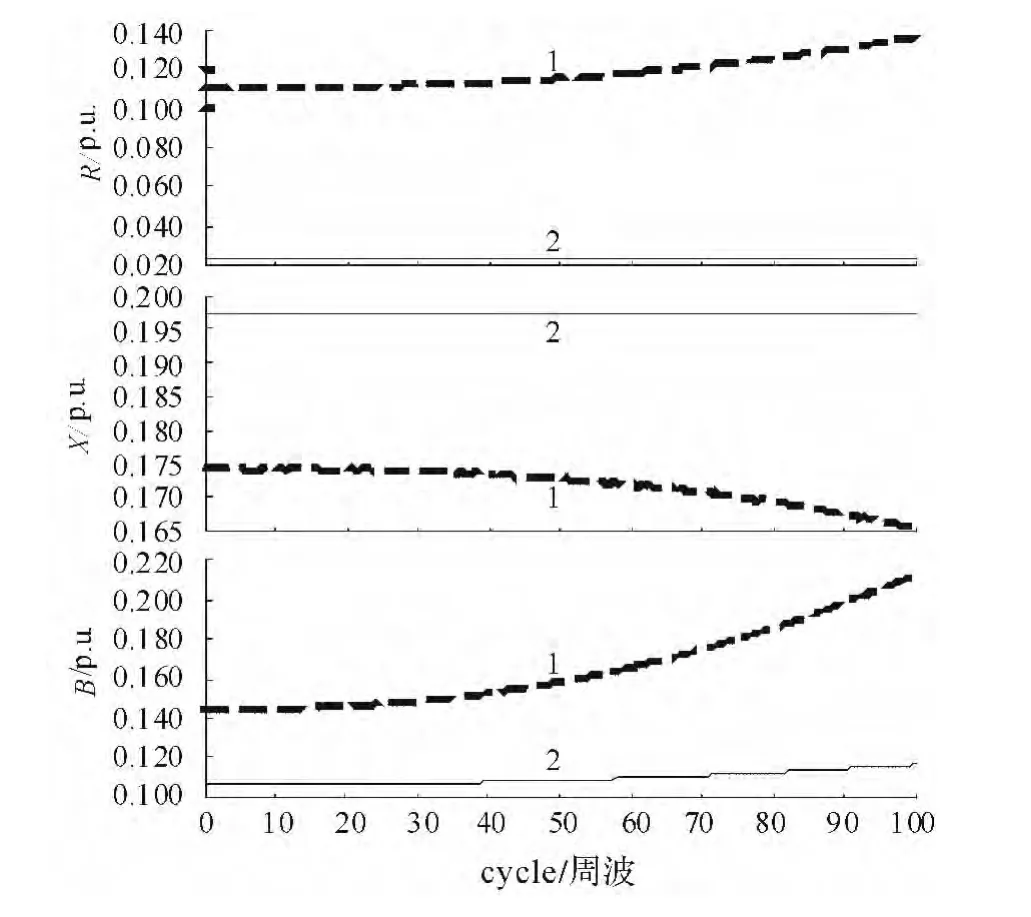
图3 采用当前测量数据线路参数辨识结果

由图3可知:随着线路上电流幅值逐渐增大，线路两端的量测数据也随之变化，进而影响线路参数辨识的精度，可见线路上潮流的大小会对线路参数辨识结果产生影响。

表2给出了利用当前测量数据辨识线路参数时两种算法 (RLS和R3LS)的计算误差对比。从表2中可以看出，R3LS算法的计算误差明显小于RLS算法，这是由于R3LS算法在目标函数中引入的正定矩阵，能够避免计算过程出现参数漂移问题，鲁棒性较强;但从线路各个参数的计算误差来看，线路电抗的计算误差最小，而线路电阻和电纳的辨识误差较大。

表2 采用当前时刻测量数据时参数计算误差

图4给出了采用多次测量数据时R3LS算法计算的输电线路参数计算结果误差图，其中曲线3表示数据窗长度为1时线路参数辨识误差图，曲线4表示数据窗长度为4时线路参数辨识误差图，设定λmin=0.95，α=5 000。经过多次仿真，可知当数据窗长度≥4时，能得到精度较高的线路辨识参数。

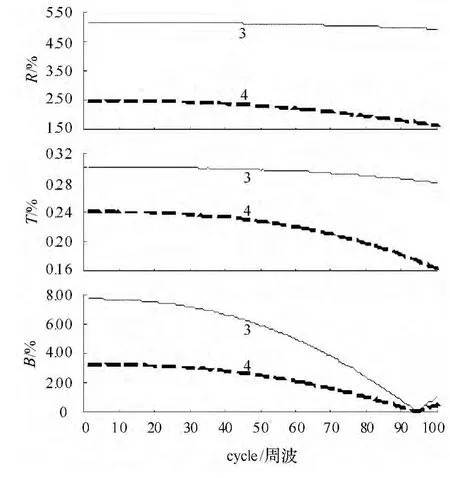
图4 输电线路参数辨识误差

从图4整体来看，增加数据窗长度计算输电线路参数能够显著减小线路的辨识误差。随着时间推移，线路上流通的电流逐渐增加，而线路辨识参数误差逐渐减小，可见线路上功率的变化对参数辨识会产生影响。

4 影响输电线路参数计算精度的因素

由式 (3)可知，输电线路参数辨识过程受到线路两端的电压相量和电流相量的影响。实际电力系统正常运行时，线路两端节点电压的幅值基本维持在额定运行点附近，变化幅度不会很大。而线路电流则会随着系统运行工况的改变而改变，因此，应重点分析输电线路上电流的变化对参数辨识结果的影响。

电网络分析中的灵敏度指网络中“网络函数”对“元件参数”的敏感程度。为了方便，本文采用增量灵敏度来分析电压、电流相量对输电线路参数辨识的影响。

假设参数x有一个微小增量Δx，引起广义网络函数T变化ΔT，那么增量灵敏度为。以输电线路电阻为例，给出电阻对节点电压和线路电流的增量灵敏度分别为:

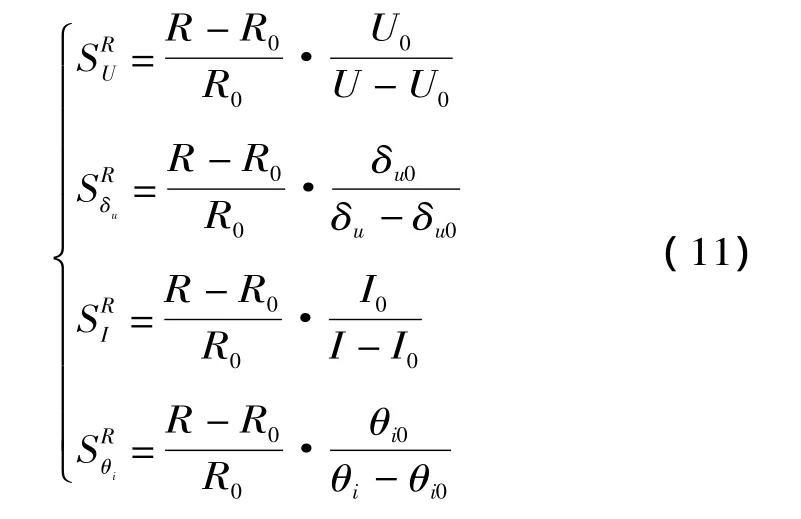
式中:，表示电阻R对节点电压和线路电流幅值的增量灵敏度;，表示电阻R对节点电压和线路电流相角的增量灵敏度。其他输电线路参数增量灵敏度表达式和电阻R类似。因此，可以通过求解输电线路参数对量测量的增量灵敏度来分析系统负荷变化对输电线路参数辨识精度的影响程度，具体如何影响有待进一步研究。

5 结论

本文依据PMU实时测量数据，借助最小二乘法对输电线路参数进行辨识，并进行了仿真验证。结果表明:(1)增加数据窗口的长度能够提高参数辨识的精度。(2)线路上流通功率的大小对线路参数辨识会产生影响，提出采用增量灵敏度的方法来分析负荷变动对输电线路参数辨识精度的影响。

［1］赵菲，焦彦军，王铁强，等.基于WAMS的输电线路参数在线辨识的研究 ［J］．电力科学与工程，2011，27(8):15-19.

［2］程冬玉，任腾军.基于最小二乘法的输电线路建设成本估算研究 ［J］．电力科学与工程，2010，26(11):24-28.

［3］杨国庆，张宇，张杨.220kV海中4634架空输电线路动态增容研究 ［J］．电力科学与工程，2012，28(1):24-29.

［4］李钦，项凤雏，颜伟，等.基于SCADA及PMU多时段量测信息的独立线路参数估计方法 ［J］.电网技术，2011，35(2):105-109.

［5］程冬玉，任腾军.基于最小二乘法的输电线路建设成本估算研究 ［J］．电力科学与工程，2010，26(11):24-28.

［6］索江镭，王尉.复合阻抗对同塔双回输电线路零序参数影响的研究 ［J］．电力科学与工程，2010，26(12):41-43.

［7］陈晓刚，易永辉，江全元，等.基于WAMS/SCADA混合量测的电网参数辨识与估计 ［J］．电力系统自动化，2008，32(5):1-5.

［8］陆进军，张力.基于PMU量测的线路参数辨识算法［J］．电网与清洁能源，2012，28(11):27-31.

［9］李大路，李蕊，孙元章，等.计及广域测量信息的状态估计错误参数识别与修正 ［J］．电力系统自动化，2009，32(14):11-15.

［10］宁辽逸，孙宏斌，吴文传，等.基于状态估计的电网支路参数估计方法 ［J］．中国电机工程学报，2009，29(1):7-13.

［11］刘焕强.输电线路参数测量方法的对比分析及现场应用 ［J］．电工技术，2006，9(9):15-17.

［12］ Flueck A J，Chiang H D，Shah K S.Investigating the installed real power transfer capability of a large scale power system under a proposed multiarea interchange schedule using CPFLOW ［J］．IEEE Trans on Power Systems，1996，11(2):883-889.

［13］王茂海，鲍捷，齐霞，等.基于PMU实测数据的输电线路参数在线估计方法 ［J］．电力系统自动化，2010，34(1):25-27.

［14］ Zhou N，Trudnowski D J，Pierre J W，et al.Electromechanical mode online estimation using regularized robust RLS methods［J］．IEEE Trans．on Power Systems，2008，23(4):1670-1681.

［15］于尔铿.电力系统状态估计 ［M］．北京:水利电力出版社，1985.

Transmission Line Parameters Estimation Based on PMU Data

Chang Xianrong，Cui Zhaojun，Zhang Haisheng
(School of Electrical and Electronic Engineering，North China Electric Power University，Baoding 071003，China)

Accurate estimation of transmission line parameters directly affects power system modeling，stability calculation and operation.Synchronous phasor technology provides a good condition for the on-line identification of transmission line parameters.In order to solve the limitation of off-line measurement，transmission line parameters identification can base on the synchronous phasor data produced by PMU.The least squares method with variable forgetting factor is introduced to on-line calculate line parameters.In this paper，an idea of using incremental sensitivity method is proposed to analyse the effect of system operation condition changes on the results of parameter identification.Simulation results of the 500 kV transmission line in a practical power system illustrate the feasibility of the present method.

transmission line;parameter estimation;recursive least squares;data window;incremental sensitivity

TM726

A

10.3969/j.issn.1672-0792.2014.04.007

2013－10－28。

常鲜戎 (1956-)，男，教授，主要研究方向为电力系统分析与控制，E-mail:changxr1@sina．com。