基于圆形天线阵的GPS抗干扰性能仿真与其干扰方法研究

王永州,夏 斌,马 辉

(63893部队,河南洛阳471000)

基于圆形天线阵的GPS抗干扰性能仿真与其干扰方法研究

王永州,夏 斌,马 辉

(63893部队,河南洛阳471000)

GPS抗干扰性能的分析有助于研究GPS干扰方法和手段。基于目前空域滤波的GPS抗干扰技术,采用LCMV算法对圆形天线阵的GPS抗干扰性能进行分析仿真,并提出了对其进行干扰的方法。在Matlab中对单个干扰源和多个干扰源在不同情况下的干扰效果进行仿真,仿真结果表明, LCMV算法能有效判定信号来波方位,并对干扰信号具有一定的赋零深度;针对分析结果提出多方位逼近干扰方法,能大幅降低LCMV获取的抗干扰增益。该方法对实战中采用空域滤波抗干扰技术的GPS干扰能提供一定的参考。

LCMV算法 抗干扰性能 多方位逼近干扰方法

0 引 言

GPS抗干扰性能的分析有助于研究GPS干扰方法和手段。目前空域滤波的GPS抗干扰技术提高了其抗干扰性能,利用天线对消技术来确定干扰的来波方向,降低干扰信号的功率和干扰效果,例如,基于干扰信号功率的功率反演算法[1-4](PI),多重信号分类算法[5](MUSIC),最小规范算法[6](Min -norm),线性约束最小方差算法(LCMV)等。基于目前空域滤波的GPS抗干扰技术,对采用LCMV算法的圆形天线阵GPS抗干扰性能进行分析仿真,在此基础上研究分析对其进行干扰的方法。

在Matlab平台上,对单个干扰源和多个干扰源在不同干扰方位下进行仿真,获取其采用LCMV算法后获取的抗干扰增益。通过分析其结果,寻找有效的GPS干扰方法。

在Matlab中对单个干扰源和多个干扰源在不同干扰方位下进行仿真,仿真结果表明,当干扰方位与信号来波方位相距较远时LCMV算法能有效判定干扰信号的来波方向,并对干扰信号具有一定的赋零深度;当干扰方向与信号来波方位相近时能降低LCMV获取的抗干扰增益。通过分析,采用多方位逼近的干扰方法,能大幅降低采用空域滤波抗干扰技术的GPS的抗干扰增益,为GPS干扰方法提供一定的参考。

1 GPS圆环阵列天线的结构模型

用于接收卫星无线电波的天线有各种各样的类型,对于阵列天线而言,有M元均匀分布的线性阵列天线,有M元均匀分布的圆环阵列天线,还有矩形阵列天线等。对于一维线性阵列天线而言,其最大缺点是对信号的来波方向判断不准(只能判断一维来波方向),而圆环阵列天线能够精确的判断信号的来波方向[3,4,7](能够判断二维来波方向),因此,这里采用圆环阵列天线作为GPS的抗干扰天线,其结构见图1。

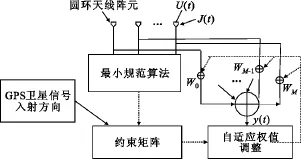
图1 GPS信号抗干扰模型结构示意Fig.1 Schematic model of GPS signal interference

由于GPS卫星距离地球表面的距离非常远,所以,在远场情况下,天线阵列总的电磁场辐射强度可表示为:

E总=E单×阵因子

假设,M个无穷小的偶极子均匀分布在圆环上,圆环半径为R,且R=λL1。如图2所示,αm是αr和αρ之间的夹角。

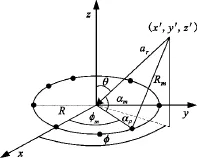
图2 圆环阵列天线结构Fig.2 Structure of ring-array antenna

对于远场辐射情况而言,幅度的变化Rm≅r。圆环阵列天线的电磁场辐射场强如下式所示:

式中,αm=Cmejgcm。Cm,gcm是第m个阵元的幅度和激励相位。因此可以得到下式:

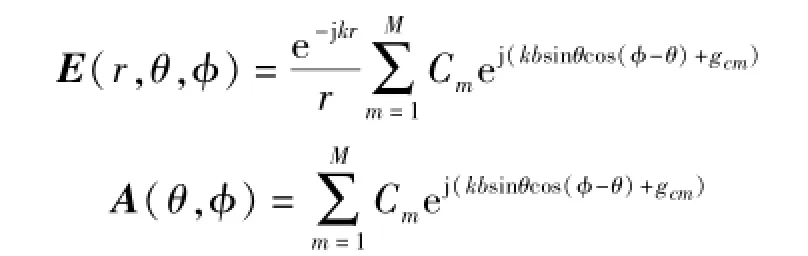
2 基于圆环阵列天线的LCMV算法

2.1 基于圆环阵列天线的最小范数算法

考虑到在均匀分布的由M个天线阵元组成的环形天线阵列上接收的信号是所有在远场情况下入射信号和噪声的线性组合,因此有:

式中,X(n)=(x1(n)x2(n)…xM(n))T是M×1的向量,表示天线阵列接收到的信号。

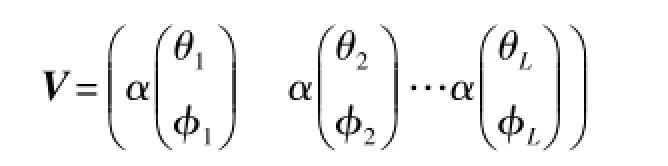
V是一个包含了与入射信号有关的控制向量矩阵。u=(u1(n)u2(n)…uL(n))T表示入射信号的幅度向量。ω=(ω0ω1…ωM-1)T是一个M×1的复数阵列权值向量。y是阵列天线的输出结果,是阵列天线的接收信号的加权和。N=(n1(n) n2(n)…nM(n))T是M×1向量,该向量由独立的高斯噪声方差σ2构成,包括信道噪声、接收机噪声和天线元噪声等。

由于天线阵元接收到的GPS信号功率低于噪声功率,接收机接收到的信号主要由噪声和干扰信号构成。假设干扰信号之间相互独立且与热噪声信号不相关。如果向量ω是由M-L维噪声子空间的特征向量的线性组合,有:

且多项式[6-7]:

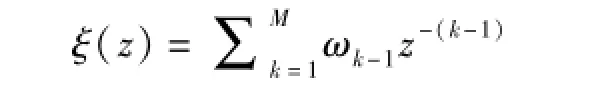
在exp(jψk)处有L个零值,k=1,2,…L。多项式ξ(z)的M-L个互不相关的零值均匀地分布在单位圆的扇区里面,在这些扇区里面,L个信号的零值是不存在的,如果式(4)中的G最小,则:

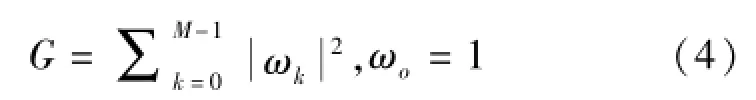
令:

要求让G最小也就是相当于令式(6)取得最小值:

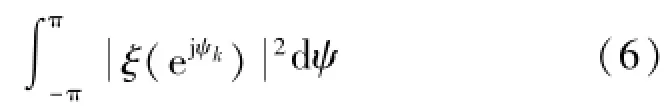
自相关矩阵用特征向量和特征值表示为:

式中:

式中,λi表示为R的第i特征值,qi是与第i的特征值有关的特征向量,i=1,2,…,M。

入射干扰信号的子空间由相应于L个最大特征值的特征向量构成。余下的[L+1:M]特征向量由噪声子空间构成。由此可得:

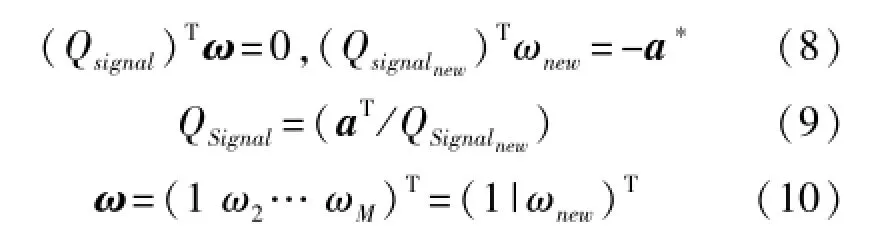
式中,aT=(q11q21…qL1)表示为每个干扰信号特征向量的第一个元素。向量ω可表示为:

2.2 基于圆环阵列天线的线性约束最小方差算法

即:

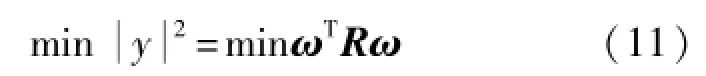
可解的:

如果不存在有用信号和干扰信号,而只存在不相关的噪声时,式(12)可变为:

式中,f=(f1f22…fK)T。

使用拉格朗日乘子法自适应计算权值向量,然后将约束方程(11)变为无约束的方程:

使输出功率最小,意味着将方程(14)关于ωT取微分,并且将结果等于零,即:

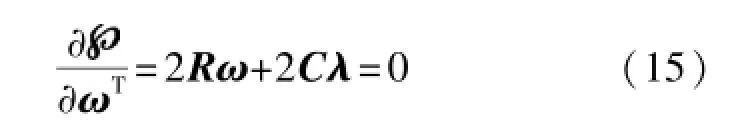
式中,λ是K×1维拉格朗日乘数向量。利用最速下降技术迭代更新权向量,可得:

由方程(15)和f=CTω(n+1)可解得λ:

式中,f是方程(11)在方程(16)中的约束部分。

将式(16)带入式(17)可得:

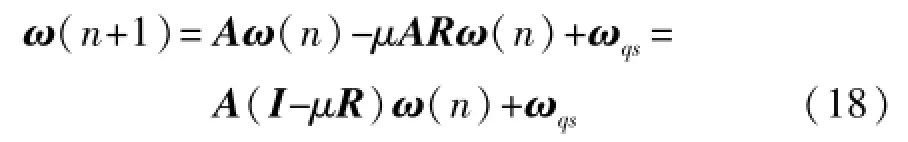
考虑到自相关矩阵R的瞬时值,R=XXT,因此,式(18)可表示为:

式中,y(n)=ωT(n)x(n)。

3 LCMV算法的Matlab仿真

Matlab对16元均匀分布的圆环阵列天线进行仿真,采用了6颗来自不同方向的有效GPS卫星,假设每颗GPS卫星信号的功率值与干扰信号功率值相等。假设N个干扰信号的来波方向与6颗GPS卫星信号的来波方向不同,并且功率电平值是固定的。该6颗有效GPS卫星信号的来波入射方向假设为:

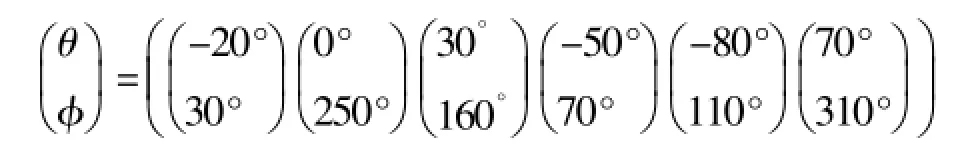
θ是入射信号方向与z轴的夹角。φ是入射信号方向与xoy平面的夹角(θ与φ如图2所示)。θ角和φ角的变化范围分别为[-90°,90°]和[0°,360°]。

如图3所示,16元均匀分布的圆环阵列天线阵在接收6颗来自不同方向的有效GPS卫星信号的波束形成图,在图3中0 dB对应于有效GPS信号功率值,其他值与此相参考。

图3 在无干扰信号下的LCMV准则下的波束形成Fig.3 Beamforming without interference signal under the guidelines of LCMV

3.1 干扰信号来波方位与GPS信号相距较远的情况

假设1个干扰信号的来波入射方向为:

约束响应形式为:

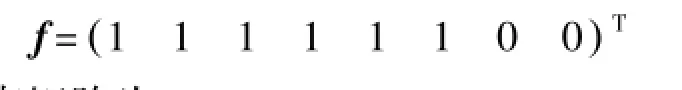
约束矩阵为:

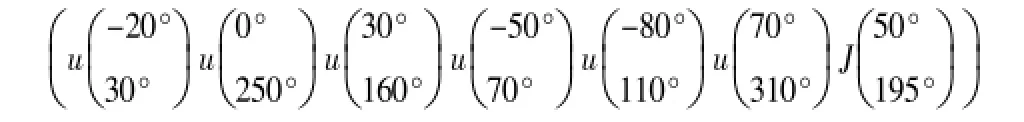
其仿真结果如图4所示,在6个来波方向上的增益为0 dB,干扰信号方向上的抑制增益为-12.7 dB。

图4 在1个干扰信号下的LCMV准则下的波束形成Fig.4 Beamforming with one interference signals under the criteria of LCMV

假设2个干扰信号的来波入射方向为:

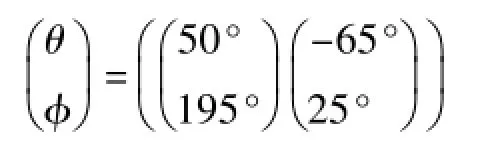
约束响应形式为:

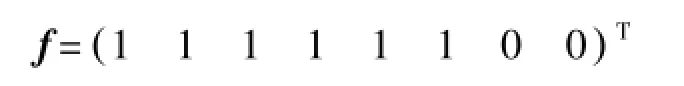
约束矩阵为:

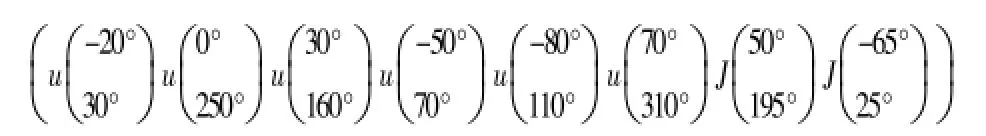
其仿真结果如图5所示,在6个来波方向上的增益为0 dB,两个干扰信号方位上的抑制增益分别为-11.4 dB和0.4 dB。

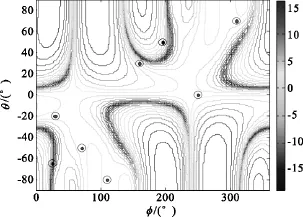
图5 在2个干扰信号下的LCMV准则下的波束形成Fig.5 Beamforming with two interference signal under the criteria of LCMV

干扰信号的干扰效果主要从干扰信号数量与天线阵元数量、干扰信号来波方位与GPS卫星信号来波方位等两方面的关系进行仿真,共分为四种情况。θ角和φ角的变化范围分别为[-90°,90°]和[0°,360°]。LCMV准则下GPS圆形天线阵抗干扰增益1见表1。

表1 LCMV准则下GPS圆形天线阵抗干扰增益1Table 1 Antijamming gain table of the cicular GPS antenna under the LCMV criteria

3.2 干扰信号来波方位与GPS信号相距较近的情况

假设干扰信号来波方位与GPS信号相距较近,其仿真结果如表2所示,当1个干扰信号时若在6个来波方向上的增益为0 dB,则干扰信号方向上的增益为-3 dB;当2个干扰信号时若在6个来波方向上的增益为0 dB,则两个干扰信号方位上的抑制增益分别为-3.2 dB和-1.4 dB。

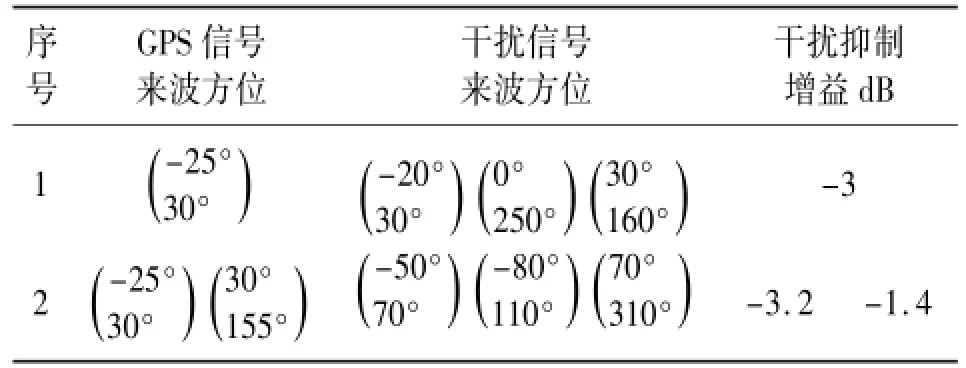
表2 LCMV准则下GPS圆形天线阵抗干扰增益2Table 2 Antijamming gain table of the circular GPS antenna under the LCMV criteria

3.3 GPS圆形天线阵LCMV算法的抗干扰性能分析

通过对GPS圆形天线阵LCMV算法的仿真结果:当没有干扰时,LCMV算法能够将兼顾不同方位上的增益;当干扰信号来波方位与有效GPS信号相距较远时,1个干扰信号的抑制增益为-12 dB,2个干扰信号的抑制增益分别为-11.4 dB和-0.4 dB;当干扰信号来波方位与有效GPS信号相距较近时, 1个干扰信号的抑制增益为-3 dB,2个干扰信号的抑制增益分别为-3.2dB和-1.4 dB。

从仿真结果看出,圆环阵列天线结合LCMV算法,能够很好的抑制1个来波方位较远的干扰信号,但无法同时抑制2个信号;当来波方位较近的干扰信号无法深度抑制。GPS圆形天线阵LCMV算法来抑制多干扰信号还存在一定的局限性。

4 多方位逼近干扰方法探讨

从仿真结论来看,多方位逼近干扰方法能够通过大幅降低LCMV获取的抗干扰增益,并降低对干扰信号的抑制增益,从而降低GPS圆形天线阵LCMV算法的抗干扰能力。根据在智能天线方面成果,该方法也能对别的算法产生一定效果,如不同来波方位的干扰信号与有效信号的总数超过阵元数量时,其抗干扰性能同样也会降低。多方位逼近干扰方法从理论上讲基本能够打破GPS采用智能天线提高抗干扰能力,但在实践中还需进一步探讨、论证和检验。

5 结 语

GPS利用圆环阵列天线并结合LCMV算法能够很好的抑制来波方位与有效信号相距较远的干扰信号,但当干扰信号数量与来波方位贴近有效信号时,其抑制能力受到一定限制。根据仿真结果和LCMV算法上的局限性,提出了采用多方位逼近干扰方法,降低GPS圆形天线阵LCMV算法的抗干扰能力。

[1]KAPLAN D E.Understanding GPS Principles and Applications[M].Norwood:Artech House Publishers,2006: 68-73.

[2]SCHWEGMAN R T,COMPTON J R.Power Inversion in a Two Elements Adaptive Array[R].Report 3433-3,E-lectro-Science Laboratory,Department Electrical Eng., Ohio State University,1972.

[3]ZAHM L C.Application of Adaptive Arrays to Suppress Strong Jammers in Presence of Weak Signals[J].IEEE Trans.Aerosp.Electron.Syst.,1973,AES-9(260): 1566-1588.

[4]COMPTON J R.The Power-inversion Adaptive Array: Concept and Performance[J].IEEE Transaction on Aerospace and Electronic Systems,1979,AES-15(06): 576-588.

[5]LU Yan-e,YANG Jun,DING Zi-ming,et al.The Orthogonal Weighted Algorithm for GPS Receiver Anti-jamming[C]//CIE International Conference on Radar Processings.Beijing,China:[s.n.],2001:15-18.

[6]KUMARESAN R,TUFTS W D.Estimating the Angles of Arrival of Multiple Plane Waves[J].IEEE Trans.Aerospace Electron.Syst.,1983(AES-19):134-139.

[7]KUMAREASAN R.On the Zeros of the Linear Prediction -erro Filter for Deterministic Signals[J].IEEE Trans. on Acoustics,Speech&Signal Processing,1983,ASSP-31(01):134-139.

王永州(1968—),男,工程硕士,高级工程师,主要研究方向为通信对抗;

WANG Yong-zhou(1968-),male,M. Eng.,senior engineer,majoring in communication countermeasure.

夏 斌(1978—),男,工程硕士,工程师,主要研究方向为通信对抗;

XIA Bin(1978-),male,M.Eng.,engineers,majoring in communication countermeasure.

马 辉(1977—),男,工程硕士,工程师,主要研究方向为通信对抗。

MA Hui(1977-),male,M.Eng.,engineers,majoring in communication countermeasure.

Simulation and Its Interference Method of Circular Antenna Array-based GPS Anti-jamming Performance

WANG Yong-zhou,XIA Bin,MA Hui
(Unit 63883 of PLA,Luoyang Henan 471000,China)

Analysis on anti-interference performance could contribute to the research of GPS interference method.Based on GPS anti-interference technique of spatial filtering,LCMV algorithm is used to analyze and simulate the GPS anti-interference performance of circular antenna array,while interference method is proposed.Simulation of interference effect with single source and multiple sources in different situations are carried out with Matlab and the simulation result shows that LCMV algorithm could be used to recognize the direction and range of signal,and to provide a certain effect of assigning null of interference signal.In accordance with the analysis,multiple direction approaching interference method is discussed,this method could reduce the gains of anti-interference with LCMV,and thus is helpful for GPS anti-interference technique of spatial filtering in actual combat condictions.

LCMV algorithm;anti-interference performance;multiple direction approaching interference method

TN929.5

A

1002-0802(2014)01-0076-05

10.3969/j.issn.1002-0802.2014.01.015