复杂网络拓扑结构的网络模型研究综述*

杨 珉,张家玥,张达敏

(贵州大学大数据与信息工程学院,贵州贵阳550025)

复杂网络拓扑结构的网络模型研究综述*

杨 珉,张家玥,张达敏

(贵州大学大数据与信息工程学院,贵州贵阳550025)

基于复杂网络拓扑结构建模能够有效地分析其结构特征和传播机理。文中从网络拓扑结构方面总结了现有的网络拓扑基本模型,以及目前的研究状况,具体介绍局域世界演化网络、自相似性网络、模块性网络、含权网络等典型模型的建立过程以及研究者们在其基础上的拓展研究。最后,在讨论目前复杂网络拓扑基本模型存在问题的同时,也提出复杂网络拓扑结构上的网络模型发展的新挑战。

复杂网络 演化 拓扑结构 动力学行为

0 引 言

复杂网络的相关研究进入中国已经有超过十年的时间了,其中的很多方向、分支都受到各个学科甚至很多交叉学科的广泛关注和研究,诸如Internet、WWW、社会关系网络、经济网络、全球交通网络、大型电力网络、科学家合作网络等[1],可以说研究这些网络的工具就是复杂网络。

复杂网络的研究一般认为是从瑞士著名的数学家Eular开创图论学科开始的,之后在相当长的一段时期没有得到发展,直到20世纪50年代末,两位著名的数学家Erdǒs和Rényi引出随机图理论,从此该发现在数学领域被公认为是开辟了复杂网络的系统性研究。1998年小世界网络[2]和1999年无标度网络[3]这两篇论文开创性地把现实世界中的网络数据抽象统计分析,研究更加符合实际网络特性的网络结构对传播过程产生了重要影响,复杂网络的

研究也发生了巨大的转变[4-6]。

钱学森先生曾给出复杂网络的一个定义:具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络称为复杂网络。当前对复杂网络的研究主要集中在三方面:①各类实际网络的拓扑结构实证研究,通过分析这些网络的拓扑性质,研究网络演化的特征与规律;②网络生成机制及演化模型的研究,确立网络演化模型,模仿真实网络行为;③复杂网络上的动力学行为研究。研究之间并不是孤立进行的,通常是复杂网络的结构决定了动力学过程,而动力学过程反过来影响网络结构的演化。

1 复杂网络模型

对于拓扑特性分析,研究者们根据建立的模型利用图论、动力学特性以及相关交叉学科的方法进行计算分析和仿真。基于现实网络存在的缺陷,更多符合实际需求的网络扩展模型被相应提出。例如,方锦清等提出随机性择优和确定性择优相结合模型[7],史定华等提出优胜劣汰模型[8]和对数增长模型[9],Saramaki等提出随机游走模型[10],Krapivsky等提出非线性择优模型[11],Dorogovtsev等提出幂律增长模型[12],郑蕾等提出的基于微博网络的信息传播模型[13]。

复杂网络的特征一般通过度分布、平均路径长度、簇系数、中心性、模体、社团分类、有效性、鲁棒性等属性进行度量。其中,基本特征有节点的度分布、聚类系数和平均路径长度。本文重点阐述典型的更加符合实际的网络拓扑结构模型,进一步探索真实网络的传播机制和拓扑结构,分析和总结基本模型及其性质,提出现有研究中存在的问题以及展望。

1.1 局域世界演化网络模型

李翔和陈关荣于2003年提出了局域世界演化网络模型[14]在BA无标度模型基础上做出了改进。局域世界网络模型不仅保持了无标度网络具有的鲁棒性,而且还改进了无标度网络面对恶意攻击所存在的脆弱性。局域世界网络模型中保留BA模型中的增长机制,也就是在每一个单位时间步长t内,加入一个新节点和m条边;而前者的全局优先连接机制被局部优先连接机制所替代,即新加入的节点从局域世界(LW)中按照择优连接概率选择M个 (M≥m)节点进行连接,而不是从整个网络中选择节点[15]。新加入的节点根据择优连接概率:

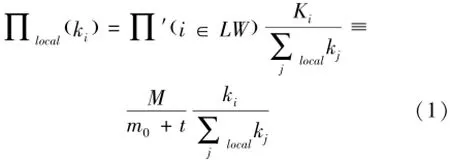
式中,m0为初始网络的节点数,M在局域世界中的个数要满足m≤M≤m0+t,即当M/m的值1≤M/m≤范围内增加时,网络中节点度的分布显示出由指数分布向幂律分布的过渡过程。局域世界网络中的节点往往比无标度网路中节点数目少,即局域世界网络中的度分布相较于随机网络、小世界网络、无标度网络中要更均匀[16]。

很多研究者在基于BA无标度网络的局域世界网络演化模型的基础上又进行改进。Xuan等首先通过节点之间度的相关性大小来判断局域世界范围的大小后,然后选取其中相关性最大的节点作为新的节点,并且通过建立局域世界网络模型和数值仿真模拟,得出度分布呈幂率分布等规律[17]。Gu等在局域世界中通过改变连接概率值和局域范围的大小构造出LWD网络模型,同时还研究得出模型度分布、聚类系数、平均路径长度等参数的变化[18]。还有田立新等构造出一个基于二分网络的类局域世界网络模型,

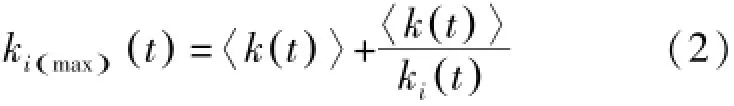
式中,ki(max)(t)为在t时刻节点i的饱和度,〈k(t)〉指的是在t时刻ki(max)节点平均度值,ki(t)指的是在t时刻节点i的度值。该网络模型根据节点的度和饱和度两项指标为标准决定该节点是否添加新节点,即是由旧节点本身的承载能力判断之后被动生成的,故称类局域世界模型[19]。

1.2 网络的自相似性

2005年Song等在分析各种实际网络后发现:很多实际网络系统,诸如社会网络、万维网、细胞网络和蛋白质交互网络等,在所有长度标度下具有自相似性结构[20]。所谓自相似性(self-similarity),即局部在某种意义上与整体相似,即就是是分形(fractal)的基本特征。复杂网络的小世界特征表明L∝ln(N)(L为网络平均路径长度,N为网络规模),其

等价表示N∝eL/L0(常数L0为特征长度),由此可发现网络规模是网络平均路径长度的指数函数,而自相似性则满足某种幂律关系[21]。

分数维这一概念随着自相似性原则的提出也引起了人们的注意。计算自相似分形维数的最常用方法之一就是盒记数法,采用该方法计算几何图形维数的思路:通过盒子(边长为lB)覆盖该图形,同时统计最少的盒子数NB(lB)直到完全覆盖该图形。这里的盒子一维是线段表示,二维是正方形表示,三维是立方体表示,盒子的尺寸即为lB。计算图形维数的近似公式:

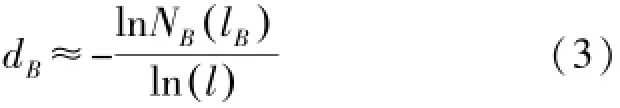
等价地有

然而复杂网络中节点间的距离表示的并非欧氏距离,而是节点间最短路径包含的边的数目。并且规定盒子尺寸lB:盒子中任意两个节点之间的距离都小于lB,一组不重叠的盒子即可重新构成一个完整的网络,即网络中所有的节点都有且仅有一个盒子覆盖。而大规模复杂网络中拥有许多不尽相同的分割方式,其中的分数维计算式(3)或式(4)中要求NB(lB)是覆盖网络的最少的盒子数,然而找到覆盖网络所需要的最少的盒子集合的问题与经典的图作色问题类似,相当于一个NP完全问题,也是复杂网络运用盒记数法的主要难点。

目前复杂网络分形大体上可分为两种研究方法:几何法和代数法。其中盒子覆盖法即为基本的几何法,比如:紧凑盒子燃烧算法、MEMB算法、贪心策略图着色算法等;代数法主要是基于网络结构与网络谱的特殊关系,研究不同网络结构导致的网络谱特征。姚灿中等创新地将计算机算法中的welch powell法应用到目前盒子覆盖算法中,有效地解决了目前盒子覆盖方法中的瓶颈问题,提高了算法效率改进了算法性能[22]。

1.3 模块性网络

一般而言,模块(module)是指一组物理上或功能上连接在一起的、共同完成一个相对独立功能的节点。模块存在于实际系统中,比如“物以类聚,人以群分”,社团在实际系统中表现为节点之间关系较为紧密、节点的特性相同或较为相近,即社团内部各节点之间表现关系相对紧密,而社团内部节点和外部节点之间关系相对疏远。网络的高聚类性表明在局部可能包含由高度连接的节点组构成的子图,模块度(modularity)的概念被Newman等首次引入,该函数是社团划分优劣程度的量化标准[23]。模块度Q的定义:

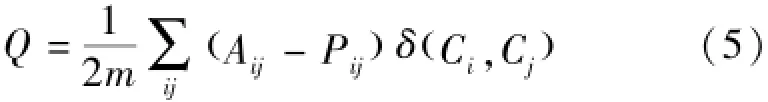
式中,A是图的邻接矩阵,m是图的边数目,Pij代表在随机图中的点i与点j之间期望的边数目,函数δ表示如果点i与点j在同一个社团中(Ci=Cj),那么函数值为1,否则为0。

基于模块度的社团发现的算法一时间也随着模块度定义的提出涌现出来,社团发现与分割问题很相似,尽管是NP难题,但研究者们也提出了许多行之有效的解决办法。其中最具代表性的算法是由Newman提出的凝聚算法,基本思想是:首先把所有节点都看作是单独的社团,然后每次迭代的时候选择两个Q值最大的社团合并,直到整个网络所有的节点都被凝聚至一个社团之内。采用凝聚算法后能够得到一个社团结构分解的树状图,最终社团结构就是从所有的社团里再选择一个局部最大的Q值社团[23]。随后,Newman和Girvan还提出了与凝聚算法思路完全相反的分裂算法,基本思想是:首先自顶向下不断地从网络中删除边的信息中心度(edge centrality)最大的边,直到又退化为每个节点单独存在的社团,然后在上一步的过程中找出对应Q值最大时的结果。通常边的信息中心度的值取为边的最短路径数[24]。还有Duch等提出的基于直接寻优算法思路的EO算法,基本思想是:首先引入一个新的局部变量,即每个节点所对应的模块度Q值贡献大小,通过初始的随机划分后,采用贪婪策略局部变量得以调整从而全局目标函数Q值也得以提高[25]。另外,还有Kernighan-Lin算法、模拟退火算法、极值优化算法的启发式搜索算法等。

很多情况下,划分网络的社团中,许多节点不仅属于一个社团而且是多个社团,该情形下的社团叫做重叠社团(Overlapping Community)。典型的重叠社区挖掘算法有:Palla等人提出的派系过滤算法(CPM,Clique Percolation Method)、Lancichinetti等人提出的基于局部扩展算法(LFM)、Lee等人提出的

贪婪团扩张算法(GCE,Greedy Clique Expansion)、刘大有等人在原始网络与相应的退火网络的结合成的集成网络上,提出重叠社区挖掘算法(UEOC,Unfold and ExtractOverlapping Communities)。

1.4 含权网络

在实际复杂系统中绝大多数网络的权值并不是0或1,节点权和连边权两个概念随着含权网络的提出也应运而生,节点权用于描绘节点的重要程度,而连边权用于描绘节点间的作用强度。边权所描绘的节点间的耦合关系多种多样,诸如,交通网络中的道路流量、Internet网络中两个路由器或两个域之间的带宽流量、社会网络中朋友的亲疏之分、科研合作网络中科学家合作的次数等,真实网络特性包括拓扑结构、动力学特征都能够从含权网络中反映出来。

Yook等提出的网络模型演化规则遵循BA无标度模型,另外在演化规则的基础上给每条新加入的边赋权,称为考虑权重的无标度网络演化模型(YJBT模型)[26]。Barrat等提出边点权值动态演化模型(BBV,Barrat-Barthelemy-Vespignani),该模型综合考虑点强度与边权值加强机制,BBV模型的动态演化利用权驱动方式得以实现,从而得出结论:节点强度、边权值和度都实现了幂率分布[27],其演化算法如下:网络初始节点m0,初始边随机连接,每一个时间步长内带有m条边的新节点j(按照节点强度择优方式)连接到初始网络中,且新边的权值为w0。新边lij的加入会造成边权(按照边权值择优方式)重新分配,权值变化如下:

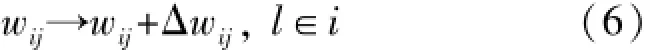
式中,Δwij=,式中si是节点强度,定义为:

式中,Ni是节点i的邻点集合。

我们可以把含权网络演化模型看作是网络拓扑结构与其承载的业务有着共生演化的耦合关系。不仅是BBV模型,还有TDE模型[28]把网络业务耦合进网络拓扑演化过程,得到网络的度、强度、权重的幂律分布以及非相称混合性和高聚集性等特征,描绘出更加符合真实工程网络的特征。

2 当前复杂网络模型存在的问题及展望

1)复杂网络的建模。基于高度动态的、过程的方法会逐渐取代基于固定结构的、静态的、线性的复杂网络研究。动态的演化过程尽管具体构造机理互不相同,但是它们基本上都遵循择优连接的机制。然而,已经有学者证实真实网络在演化过程中并不是完全遵守严格的择优机制,而是随机和择优两种机制共同作用的结果[29]。还有许多实际网络是由多个个体或子系统由于相互作用而融合为网络,这时就需要新的度量指标和特定的新型工具来描述和模拟网络间的相互作用和影响。复杂网络的理论模型以及网络的拓扑构造方法、网络特征参数度量还需要更加深入研究。

2)含权网络的权重与拓扑结构。节点与节点间的最短路径可由权重随机化直接影响,从而影响到点、边介数,因此网络的全局拓扑结构特征仅仅利用权重随机化就可以改变。方锦清等在对实际网络(包括恒河猴网络、经济物理科学家合作网络等)进行了多次划分,发现加权网络、无权网络和反权网络之间社团结构具有显著差别,认为权重与边的匹配方式对于社团结构划分具有重要的影响。然而现实网络中(比如交通流量)在网络负载足够的情况下,网络拓扑结构不一定会随着网络权重的变化而变化,因此关于含权网络权重与拓扑结构的研究还有很多实际问题值得探讨[30]。

3)复杂网络演化的复杂性。某些真实网络系统中出现的一些复杂现象,有的还没得到很合理的解释,其成因也缺乏研究,比如复杂网络的自组织临界性;网络的拓扑结构变化对网络动力学行为的影响也少有研究,因此带有反馈功能的自适应网络的动力学行为值得深入探索。许多研究成果单从物理学角度并没有考虑网络的实际功能和现实条件的限制,特别是针对网络工程。许多关于应用方面的文献叙述的都是在某个方面对某个特殊领域的网络化,并进行网络的结构分析与定性讨论,还需要一些深入的应用研究如何根据具体的应用场景有针对性地选择合适的方法。近年来众多的研究成果还停留在从真实网络到理论模型的建立和分析上,想要把科学研究的结果返回到网络工程去检验和实现,还有相当长的一段路要走。

4)复杂网络的规模。由于大数据时代的到来,复杂网络的规模也日益扩大,目前以单机资源为主的复杂网络研究迎来了巨大的挑战。不管是复杂网

络的数据存储还是大型运算,即使单机配置了更大容量的存储设备和更高处理能力的处理器,其结果也收效甚微。一个有效的解决办法就是采用由多台单机组成的集群进行分布式存储与处理;另一种解决办法是利用云计算技术,在云计算的环境下处理我们的任务既提升了研究的高度、提高了工作的效率,也增加了技术的灵活性。在云计算的环境下,例如Map Reduce、Erlang等编程框架也可以用于实现任务算法。

3 结 语

基于复杂网络理论的拓扑演化能够从网络拓扑的角度揭示复杂网络结构特征对复杂网络本身的影响。复杂网络是物理学、数学、计算机科学、生物学、社会学等学科之间的桥梁。如,医学家希望了解传染病是如何在人群中传播的并希望找到有效的预防和控制策略;社会学家关心谣言、舆论观点等信息是如何在社会上传播的;网络安全专家关心各种计算机病毒是如何在Internet上传播的。研究复杂网络模型可以有效地分析传播动力学行为及度量指标,从而提出相应有效的防御和控制策略,进而达到降低网络安全风险、提高网络运行效率、优化网络设计结构等现实目的。论文中错漏和不妥之处在所难免,敬请专家批评指正。

[1] 周涛,张子柯,陈关荣,等.复杂网络研究的机遇与挑战[J].电子科技大学学报,2014,43(01):1-5.

ZHOU Tao,ZHANG Zi-Ke,CHEN Guan-rong,et al.The Opportunities and Challenges of Complex Network Research[J].Journal of University of Electronic Science and Technology of China,2014,43(1):1-5.

[2] Watts D J,Strogatz S H.Collective Dynamics of Small-World Networks[J].Nature,1998,393(6684):440-442.

[3] Barabási A L,Albert R.Emergence of Scaling in Random Networks[J].Science,1999(286):509-512.

[4] 方锦清,汪小帆,郑志刚.非线性网络的动力学复杂性研究[J].物理学进展,2009,29(01):1-74.

FANG Jin-qing,WANG Xiao-fang,ZHENG Zhi-gang. Dynamical Complexity of Nonlinear Networks[J].Progress in Physics,2009,29(1):1-74.

[5] SHID H,LIU L,ZHU SX,et al.Degree distribution of evolving networks[J].Europhysics letter,2006,76 (04):10315-10316.

[6] SHID H,CHEN Q H,LIU L M.Markov chain-based Numerical Method for Degree Distribution of Growing Networks[J].Physical Review E,2005,(71):036140-036148.

[7] Saramaki J,Kaski K.Scale-free Networks Generated by Random Walkers[J].Physica A,2004,341(11):80-86.

[8] Krapivsky P L,Redner S,Leyvraz F.Connectivity of Growing Random Networks[J].Physics Review Letters, 2000,85(21):4629-4632.

[9] Dorogovtsev S N,Mendes J F F.Effect of the Accelerating Growth of Communication Networks on Their Structure[J]. Physical Review E,2001,63(06):025101-025104.

[10] 周涛,韩筱璞,闫小勇,等.人类行为时空特性的统计力学[J].电子科技大学学报,2013,42(07):481-540.

ZHOU Tao,HAN Xiao-pu,YAN Xiao-yong,et al.Statistical Mechanics of the Temporal Characteristics of Human Behavior[J].University of Electronic Science and Technology,2013,42(7):481-540.

[11] 陈关荣.复杂动态网络环境下控制理论遇到的问题与挑战[J].自动化学报,2013,39(04):312-321.

CHEN Guan-rong,Issues and Challenges of Control Theory based on a Complex Dynam ic Network Environment.Acta Automatica Sinica,2013,39(4):312-321.

[12] Nepusz T,Vicsek T.Controlling Edge Dynamics in Complex Networks[J].Nature Physics,2012,8(07):568-573.

[13] 郑蕾,李生红.基于微博网络的信息传播模型[J].通信技术,2012,45(02):39-41.

ZHENG Lei,LISheng-hong.A Novel Information Diffusion Model based on Microblog Network[J].Communications Technology,2012,45(2):39-41.

[14] LIX,CHENG R.A Local-world Evolving Network Model [J].Physics Letters A,2003,328(02):287-296.

[15] 许丹,李翔,陈关荣.局域世界复杂网络中的病毒传播及免疫控制[J].控制与决策,2006,21(07):817-820.

Xu D,Li X,Chen G R.Local World Complex Network of Transmission of the Virus and Immune Control[J]. Control and Decision,2006,21(7):817-820.

[16] 汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].北京:清华大学出版社,2006:4-5.

WANG Xiao-fang,LI Xiang,CHEN Guan-rong.Complex Network Theory and its Application[M].Beijing: Tsinghua University Press,2006:4-5.

[17] XUAN Q,LIY,WU T J.A Local-World Network Model based on Inter-node Correlation Degree[J].Physica A, 2007(378):561-572.

[18] GU Y Y,SUN JT.A Local-World node Deleting Evolving Network Model[J].Physics Letters A,2008,372 (25):4564-4568.

[19] 田立新,贺莹环,黄益.一种新型二分网络类局域世界演化模型[J].物理学报,2012,61(22):228903.

TIAN Li-xin,JIA Ying-huan,HUANG Yi.A New Class of LocalWorld Bipartite Network Evolution Model[J]. Physics,2012,61(22):228903.

[20] SONG C,Jalvin S,Makse H A.Self-similarity of Complex Networks[J].Nature,2005(433):392-395.

[21] 王江涛,杨建梅.复杂网络的分形研究方法研究[J].复杂系统与复杂性科学,2013,10(04):1-7.

WANG Jiang-tao,YANG Jian-mei.Fractal Study of Complex Networks Research Methods[J].Complex Systems and Complexity Science,2013,10(4):1-7.

[22] 姚灿中,杨建梅.复杂网络分形的盒维数改进算法[J].计算机工程与应用,2010,46(08):5-7.

YAO Can-zhong,YANG Jian-mei.Box Fractal Dimension of Complex Networks Improved Algorithm[J].Computer Engineering and Applications,2010,46(8):5-7.

[23] Newman M E J.Fast Algorithm for Detecting Community Structure in Networks[J].Physical Review E,2004, 69(06):066133.

[24] Newman M E J,Girvan M.Finding and Evaluating Community Structure in Networks[J].Physical Review E, 2004,69(02):026113-026128.

[25] Duch J,Arenas A.Community Detection in Complex Networks Using External Optimization[J].Physical Review E,2005,72(07):027104.

[26] Yook SH,Jeong H,Barabási A L.Weighted Evolving Networks[J].Physical Review Letters,2001,86(25): 5835-5838.

[27] Barabási A L,Barthelemy M,Vespignani A.Weighted Evolving Networks:Coupling Topology and Weight Dynamics[J].Physical Review Letters,2004,92(22): 228701.

[28] 汪秉宏,王文旭,周涛.交通流驱动的含权网络[J].物理,2006,35(04):304-310.

WANG Bing-hong,WANG Wen-xun,ZHOU Tao.A Weighted Complex Network Model Driven by Traffic Flow[J].Physics,2006,35(4):304-310.

[29] 蒋国平,宋玉蓉,巩永旺.基于复杂网络结构特征的病毒传播研究综述[J].南京邮电大学学报:自然科学版,2012,32(05):1-5.

JIANG Guo-ping,SONG Yu-rong,GONG Yong-wang. Summary based on Complex Structural Characteristics of the Network Transmission of the Virus[J].Nanjing University of Posts and Telecommunications:Natural Science,2012,32(5):1-5.

[30] 吕琳媛,陆君安,张子柯,等.复杂网络观察[J].复杂系统与复杂性科学,2010,7(2-3):173-187.

LV Lin-yuan,LU Jun-an,ZHANG Zi-ke,et al.Looking into Complex Networks[J].Complex Systems and Complexity Science,2010,7(2-3):173-187.

杨 珉(1989—),女,硕士研究生,主要研究方向为复杂网络;

YANG Min(1989-),female,graduate student,majoring in complex networks.

张家玥(1988—),女,硕士研究生,主要研究方向为复杂网络;

ZHANG Jia-yue(1989-),female,graduate student,majoring in complex networks.

张达敏(1967—),男,教授,主要研究方向为计算机应用技术、网络拥塞控制、病毒传播机制。

ZHANG Da-min(1967-),male,professor,majoring in computer application technology,network congestion control and virus propagationmechanisms.

Overview on Network Models of Complex Networks Topology Structure

YANGMin,ZHANG Jia-yue,ZHANG Da-min
(College of Big Data and Information Engineering,Guizhou University,Guiyang Guizhou 550025,China)

Modeling based on complex network topology structure could effectively analyze its structural characteristics and propagationmechanism.In terms of network topology structure,this paper summarizes the basic models of existing network topology and the research status.Then it introduces in detail the setup procedure and research extension of several typicalmodels,such as local-world evolving network,the self -similarity network,themodule network,the weighted network.Fianlly,the current issues of complex network topology basic model are discussed,and meanwhile,the new challenges in the development of network model on complex network topology structure are also pointed out in this paper.

complex network;evolution;topology;dynamic behavior

TP393

A

1002-0802(2014)12-1354-06

10.3969/j.issn.1002-0802.2014.12.002

2014-09-12;

2014-10-21 Received date：2014-09-12;Revised date：2014-10-21

贵州省省委组织部项目(No.TZJF-2011-37);贵州省合作计划项目([2012]7002号);贵州大学研究生创新基金项目(研理工2014005)

FoundationItem:Guizhou Provincial Party Committee Organization Department of the Project(TZJF-2011-37),Cooperation Projects of Guizhou Province([2012]No.7002),Guizhou University Graduate Innovation Fund(Research of Technology 2014005)