应用开关磁阻电机激励参数控制转矩脉动仿真
2014-02-08孙晓明
孙 晓 明
(江阴职业技术学院 电子信息工程系,江苏 江阴 214405)
0 引 言
开关磁阻电机(Switched Reluctance Motor,SRM)有结构简单坚固、效率高、调速性能优越等优点[1],成为目前调速驱动系统中的新成员。由SRM定转子双凸极结构和非线性电磁特性决定的转矩脉动是SRM的主要缺点[2-3],转矩脉动引起的振动和噪声限制了SRM的应用,譬如伺服驱动等低速要求平稳的场合。所以如何控制SRM转矩脉动是一项值得研究的课题。控制SRM转矩脉动主要有两种方向:一是电机结构参数优化设计[4];二是选择合适的电机控制方式[5-6]。这里采用开通角自调整、关断角模糊补偿的控制方式,以六相12/10电机为例构建系统仿真模型控制SRM转矩脉动。
1 SRM数学模型
六相12/10结构SRM一相主电路图见图1,给出了A相绕组及其供电电路[7],S1、S7是主开关管,VD1、VD7为续流二极管,U0为励磁电压。
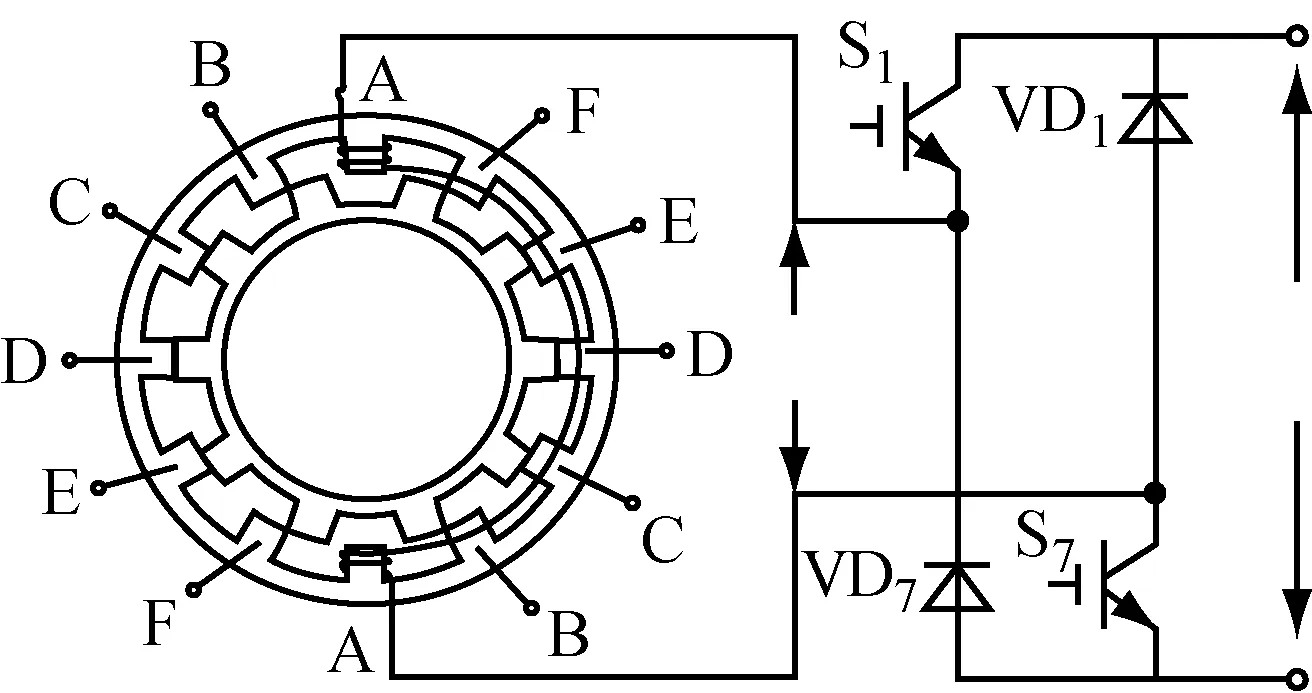
图1 六相12/10结构SRM一相主电路图
SRM运行时,随着转子位置和相电流的变化,磁链和相电感也是一直在变化,SRM非线性简化模型是相电流和转子位置的函数,相电感随着转子位置角周期性变化而周期性变化的,可以用一个关于转子位置角的傅立叶级数来表示[8-9]:
(1)
式中:L为相电感,Nr为SRM转子极数(这里Nr=10);i为相电流;θ为转子位置角。
SRM动态过程由电路方程、机械方程、机电方程三部分组成。SRM一相电动势平衡方程式:
(2)
式中:U0为相绕组端电压即励磁电压;R为相绕组电阻;Ψ为相绕组磁链,Ψ可以如下表达:
Ψ=L(θ,i)·i
(3)
SRM机械方程如下:
式中:Te为SRM转矩;TL为负载转矩;ω为角速度;J为转动惯量,f为摩擦系数。
SRM相转矩及六相总电磁转矩如下:
2 SRM转矩脉动控制策略
如果给定转速和相绕组电流,SRM就有一个使转矩脉动最小的关断角[10-11]。由此,对12/10型SRM,先定义关断角初始位置,采用模糊控制实现SRM的关断角补偿, 减小转矩脉动。
对于H桥功率变换器,SRM退磁阶段相电流用以下表达式表示:
式中:i0为退磁初始相电流;-U0为退磁电压;c为退磁时间常数;θoff为关断角;L(θoff)为关断角时相电感;Ri为相绕组阻抗。
相电流减小到零的时间ti表达式:
(11)
式(11)表明,对于给定角速度ωref和退磁初始相电流i0,可通过模糊补偿θoff进而调整ti,优化相电流,控制转矩及转矩脉动。
关断角模糊补偿控制选用二维模糊控制器[12],输入为给定角速度ωref与参考相电流Iref,输出量为关断角补偿量Δθoff。关断角模糊变量隶属函数如图2所示,Δθoff模糊规则如表1。关断角确定先定义关断角初始位置18°,再加补偿量,即:
θoff=18°+Δθoff
(12)
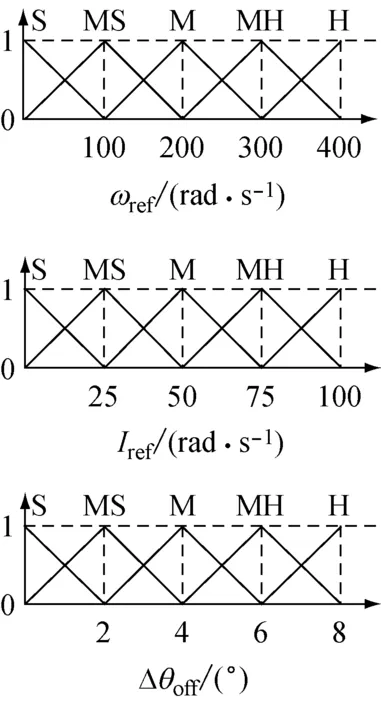
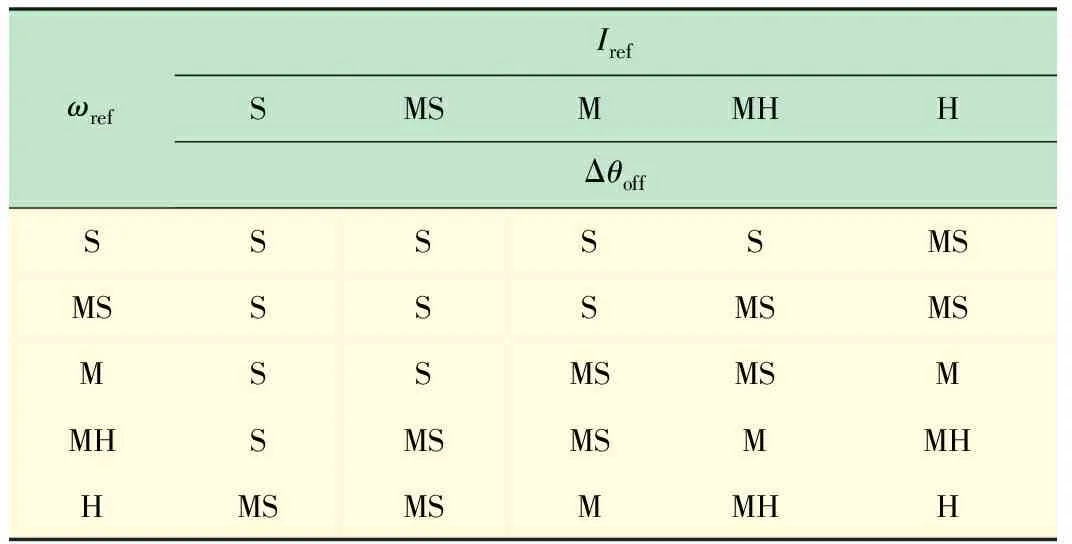
图2 关断角模糊变量隶属函数
转矩脉动控制采用关断角模糊补偿,由于滞后关断角,会使相电流延伸到电感下降段,可能产生反向转矩,电机出力减小。对于这样的问题,采用开通角自调整方式,优化相电流,平衡反向转矩,提高平均转矩。引用开通角分析表达式[13](13)确定开通角自调整公式(14)并设计开通角自调整控制器如图3所示。
式中:θon为开通角;θm为相电流峰值期望位置;Lmin为最小电感;U0为励磁电压;Δθon为开通角调整量。
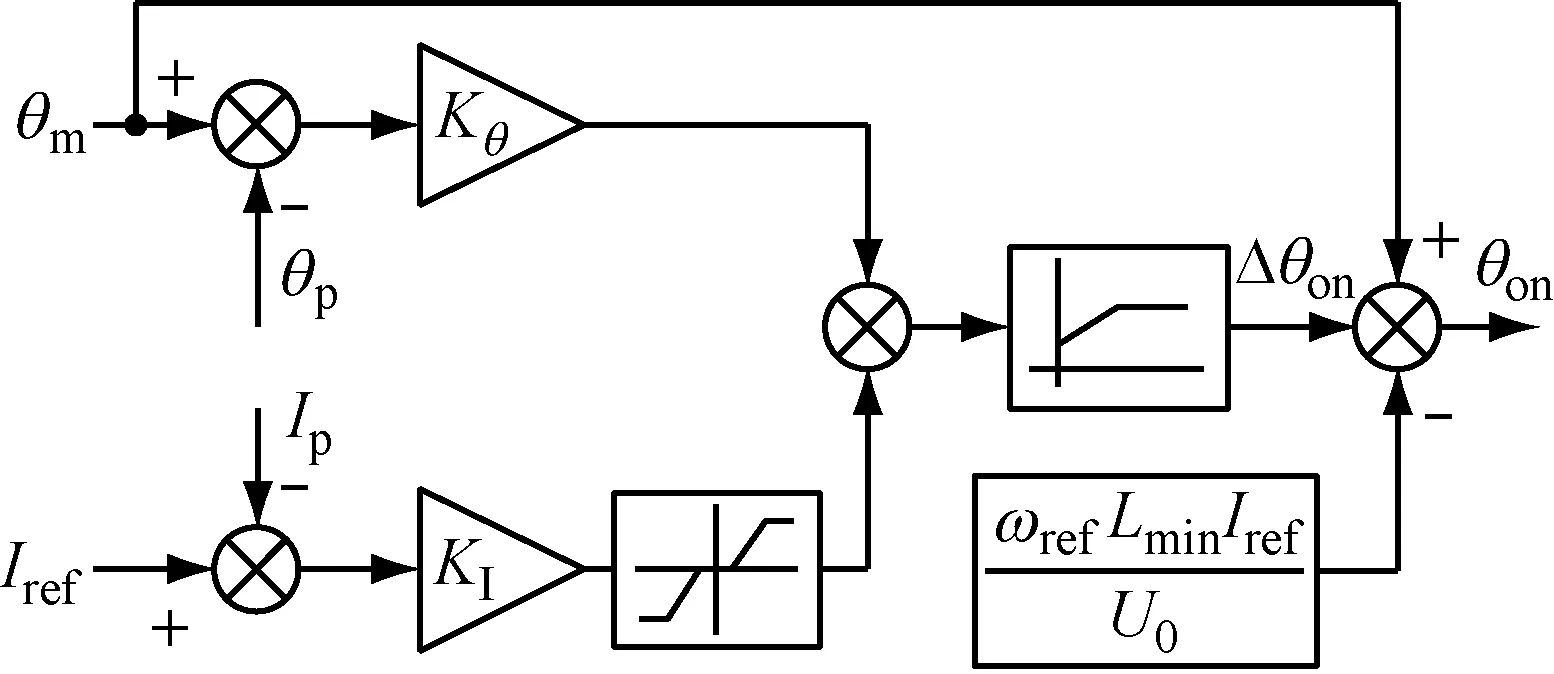
图3 开通角自调整控制器
开通角自调整控制器,持续监控相电流实际峰值Ip与实际位置θp。当SRM运行在低速时,采用电流斩波控制方式(Chopped Current Control,CCC),相电流以Iref为斩波限,Ip=Iref,KI不起作用,此时将θp与θm比较,根据差值提前或者滞后开通角,目标是将θp位置调整到θm。当SRM在中高速时,采用角度位置控制(Angle Position Control,APC)方式,相电流为单脉冲方式,θp=θm,Kθ不起作用,此时将Ip与Iref作比较,调整开通角。
3 SRM转矩脉动仿真
六相12/10开关磁阻电机参数:电机功率1.5 kW、最高转速4 000 r/min、定子极数12、转子极数10、定子极弧系数0.45、转子极弧系数0.35,励磁电压36 V,应用Matlab建立了仿真模型[15-16]。图4为CCC控制方式,转速500 r/min,参考相电流50 A,开通角自调整仿真。图5为APC控制方式转速2 000 r/min,开通角自调整仿真。图6为转速800 r/min,参考电流50 A,关断角模糊补偿仿真。从仿真可以看到通过采用开通角自调整,关断角补偿的方式,转矩脉动在减小,平均转矩在增大。
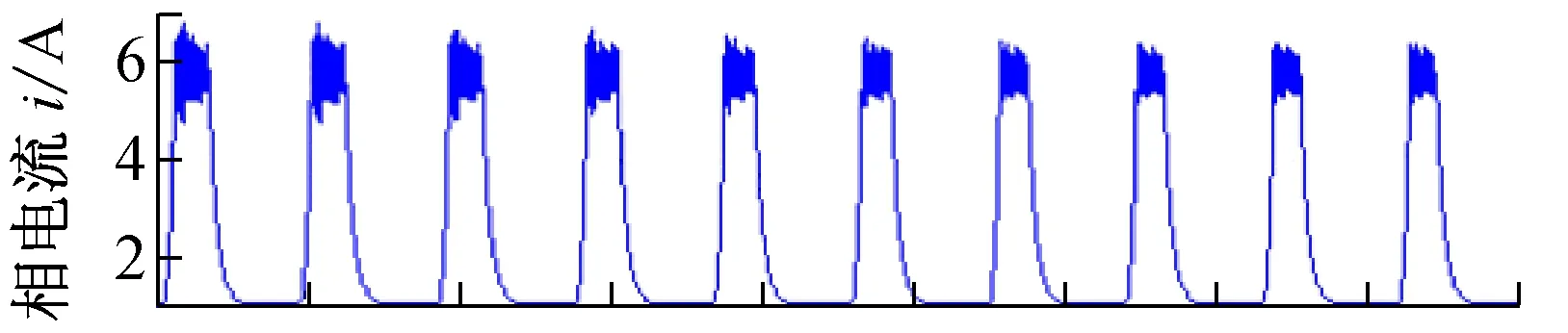
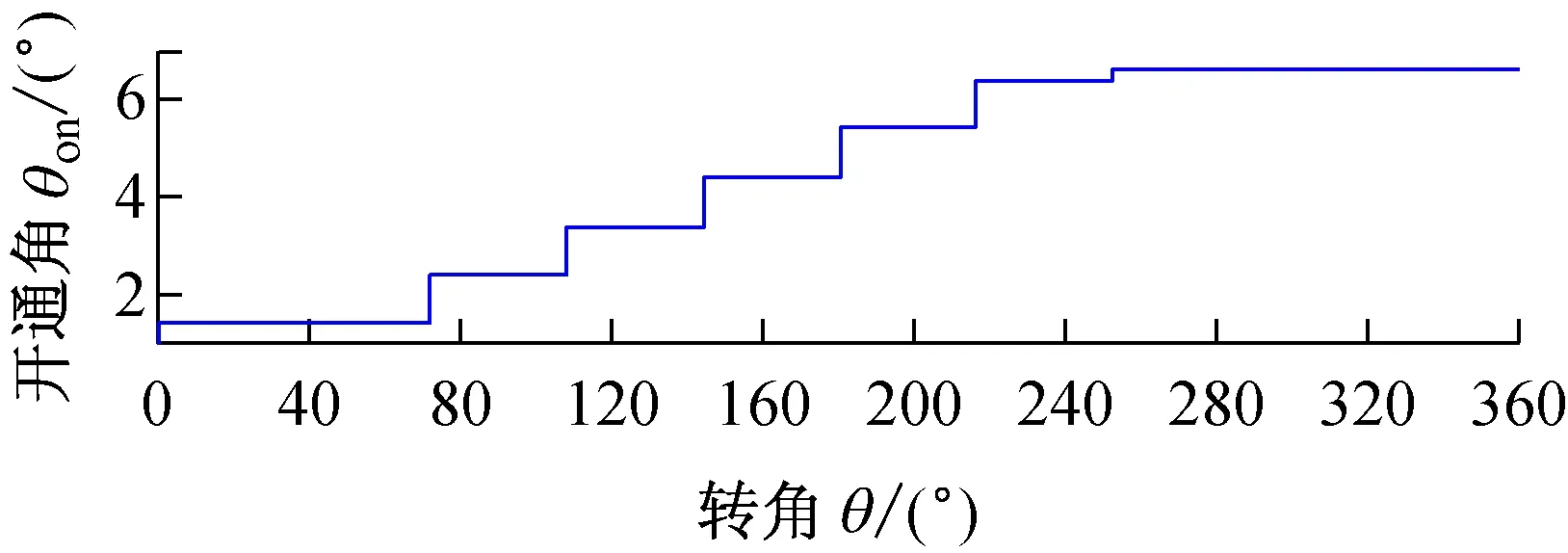
图4 CCC方式开通角自调整仿真
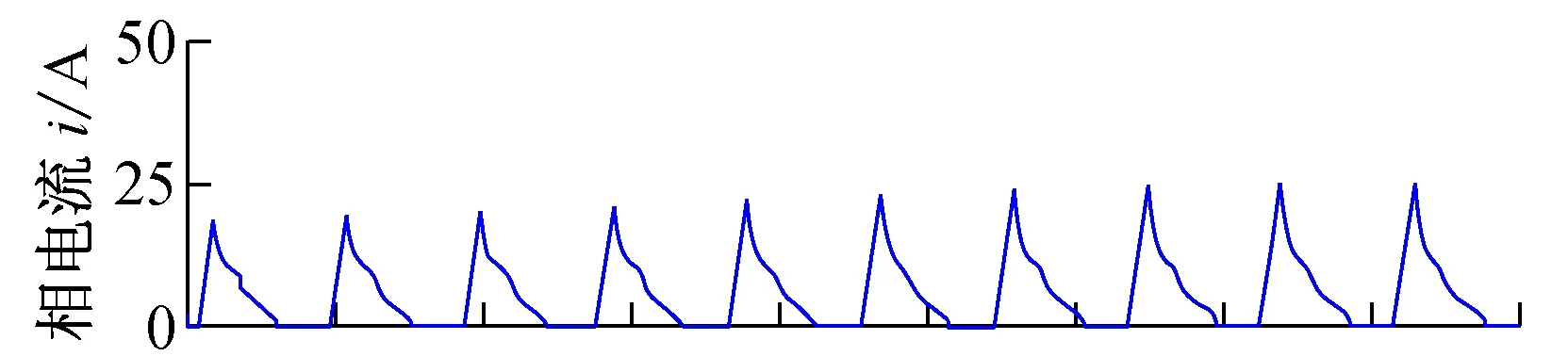
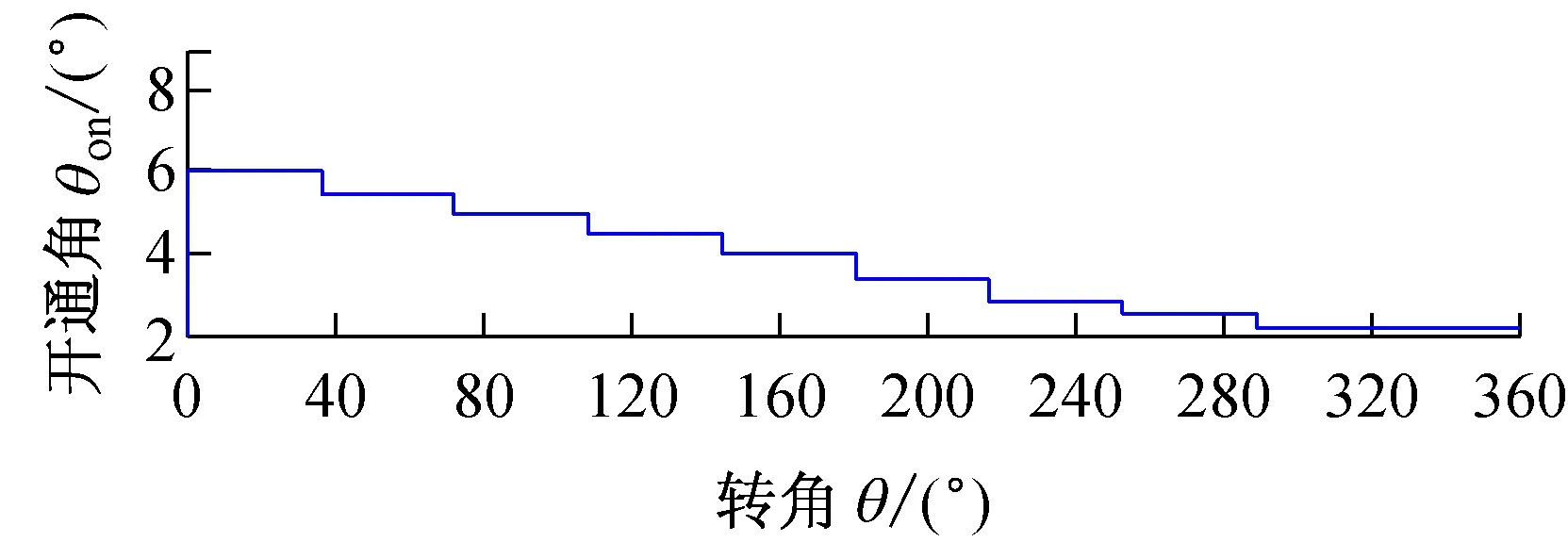
图5 APC方式开通角自调整仿真
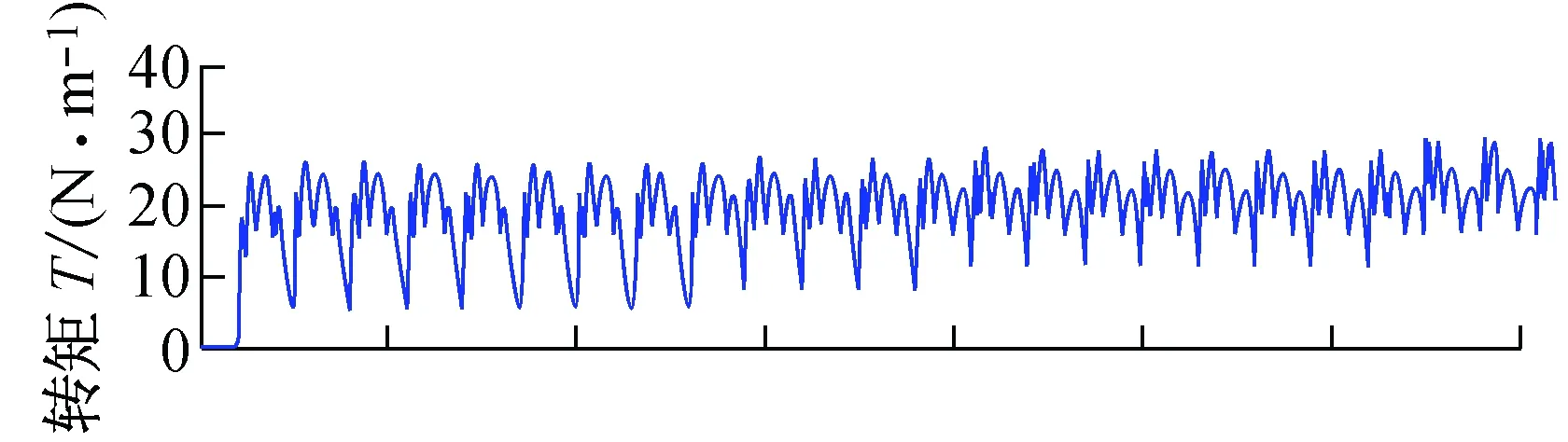
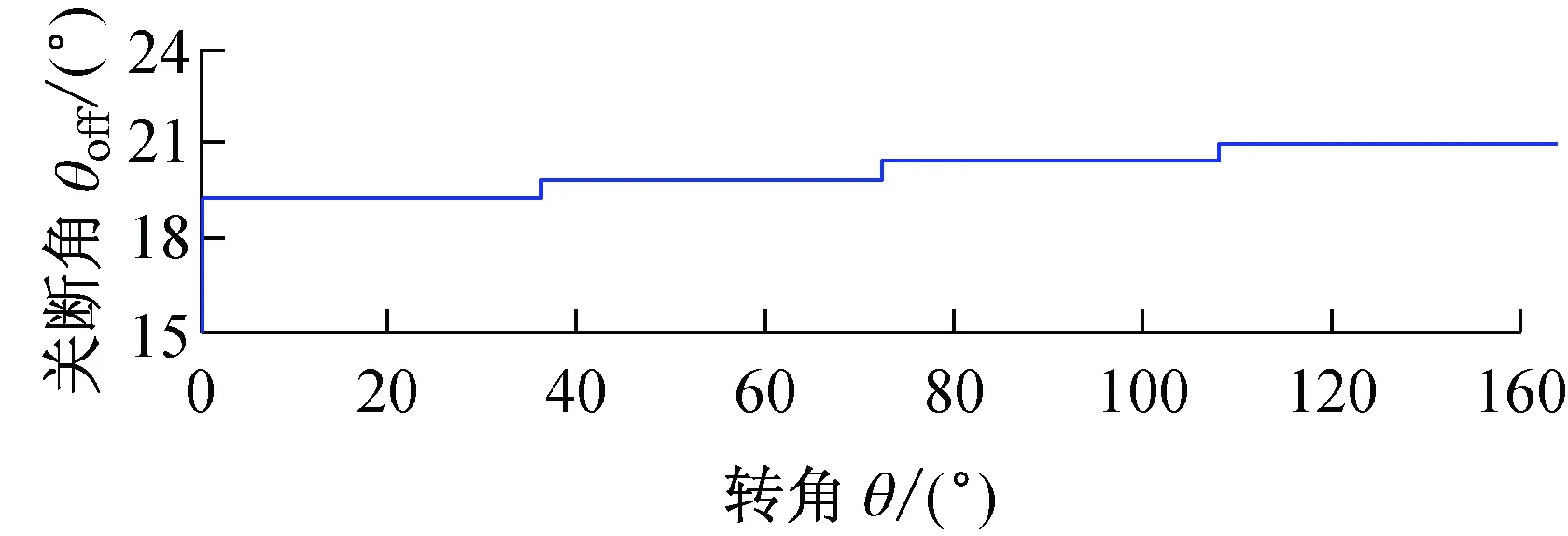
图6 关断角模糊补偿仿真
4 结 语
开关磁阻电机转矩脉动控制问题一直是热点,由此建立SRM非线性简化数学模型,采用关断角模糊补偿方式控制转矩脉动,模糊控制对电机时变性有较好的适应能力,由关断角补偿带来的反向转矩问题,通过开通角自调整,平衡反向转矩,提高平均转矩输出,仿真表明以上控制策略是可行的,同时该方法简单可靠、易于在实际系统实现、鲁棒性好。
[1] 王宏华.开关型磁阻电动机调速控制技术[M].北京:机械工业出版社,1999.
[2] 吴建华.开关磁阻电动机设计与应用[M].北京:机械工业出版社,2000.
[3] 雷 涛,林 辉. 开关磁阻电机调速中转矩脉动最小化的研究[J].电气传动,2006,36(4):3-7.
LEI Tao,LIN Hui. Study of Minimization of Torque Ripple in SRM Drives[J]. Electric Drive,2006,36(4):3-7.
[4] 张慧英, 汪旭东, 高彩霞. 开关磁阻电机转矩脉动最小化研究[J]. 微电机,2009,42(9):15-17.
ZHANG Hui-ying,WANG Xu-dong,GAO Cai-xia. Study of Minimum Torque Ripple for Switched Reluctance Motor[J]. Micromotors, 2009, 42(9):15-17.
[5] 周素莹,林 辉.减小开关磁阻电机转矩脉动的控制策略综述[J]. 电气传动,2008,38(3):11-17.
ZHOU Su-ying, LIN Hui. Overviews of Control Strategies to Minimize Torque Ripple of Switched Reluctance Motor[J]. Electric Drive, 2008,38(3): 11-17.
[6] 吴红星,赵 哲,稽 恒,等.抑制开关磁阻电动机转矩波动控制方法综述[J].微电机,2010, 43(1): 78-85.
WU Hong-xing,ZHAO Zhe,JI Heng,etal. Review of Control Strategies to Minimize Torque Ripple of Switched Reluctance Motor[J]. Micromotors, 2010,43(1):78-85.
[7] 席 艳,邵 达,贡 亮.开关磁阻电机功率电路的设计和保护[J]. 实验室研究与探索, 2013,32(8):249-252.
XI Yan,SHAO Da,GONG Liang. Design and Protection of the Power Circuit for SRD System[J]. Research and Exploration in Laboratory, 2013,32(8):249-252.
[8] 孙晓明,赵德安,李 瑶,等.基于MATLAB的开关磁阻电机非线性建模仿真[J].电力系统及其自动化学报,2006,18(1):67-70.
SUN Xiao-ming, ZHAO De-an, LI Yao,etal. Nonlinear Modeling and Simulation of Switched Reluctance Motor Using MATLAB[J]. Proceedings of the CSU-EPSA, 2006,18(1):67-70.
[9] 孙晓明.发动机怠速脉动开关磁阻电机主动阻尼控制[J].电力系统及其自动化学报,2009,21(3): 121-124.
SUN Xiao-ming.Switched Reluctance Motor Active Damping Control for Engine Idle Speed Oscillation[J].Proceedings of the CSU-EPSA,2009, 21(3): 121-124.
[10] Rodrigues M, Costa Branco P J,Suemitsu W, Fuzzy Logic Torque Ripple Reduction by Turn-off Angle Compensation for Switched Reluctance Motors[J]. IEEE Transactions on Industrial Electronics,2001, 48(3):711-715.
[11] 汤小君,易灵芝,朱建林,等. 非线性模型的开关磁阻电动机转矩脉动抑制[J].电机与控制学报, 2007,11(2):120-124.
TANG Xiao-jun, YI Ling-zhi,ZHU Jian-lin,etal. Torque ripple reduction in switched reluctance motor based on the nonlinearmodel[J].Electric Machines and Control, 2007,11(2):120-124.
[12] 刘金琨.先进PID控制及其MATLAB仿真[M]. 北京:电子工业出版社,2003.
[13] Yilmaz Sozer, David A Torrey, Erkan Mese. Automatic Control of Excitation Parameters for Switched-Reluctance Motor Drives[J]. IEEE Transactions on Power Electronics,2003,18(2): 594-603.
[14] 赵德安.车用开关磁阻电机ISAD系统的先进控制方法研究[D].南京:南京航空航天大学,2007.
[15] Soares F,Costa Branco P J. Simulation of a 6/4 switched reluctance motor based on Matlab/Simulink environment[J]. IEEE Transactions on Aerospace and Electronic Systems,2001,37(3): 989-1009.
[16] 石辛民.模糊控制及其MATLAB仿真[M]. 北京: 清华大学出版社,2008.
