地铁盾构隧道轴线测量及纠偏曲线设计

孙晓丽，李效超，王智

(青岛市勘察测绘研究院，山东青岛 266032)

1 引言

目前在地铁建设中，主要采用盾构挖掘法进行施工。盾构法是用来挖掘地铁隧道的较好选择，特别适于软土地质的施工。在盾构施工过程中，测量工作非常重要，是保证隧道顺利竣工的关键环节。盾构机向前推进一个管片环宽的距离，随后在尾部进行管片的拼装，使之形成衬砌，同时实施壁后注浆，以控制开挖面及围岩的稳定。各个管片中心的连线即是盾构机实际的开挖线，使之与设计轴线进行对比便可知开挖方向的偏差量［1，2］，因此测量已拼装管片轴线的三维坐标是检测隧道开挖质量的重要措施。

盾构推进时，需要及时获取盾构位置和姿态信息，并将盾构机的实际空间坐标与隧道设计轴线上的对应的坐标值进行比较，判断施工线路对设计轴线的拟合状况，在出现偏差时进行及时纠偏［3，4］。因此，纠偏判别是盾构施工的重要一环。当偏差量较小时，可以通过选择合适的管型和安装点位进行纠偏;当超过管片纠偏范围时，则需要设计纠偏曲线，通常情况下，采用设计线形中取用规范标准的最小限值或与限值接近的大曲率小半径曲线来连接盾构机现状位置和设计曲线［4］。

2 轴线测量

轴线测量的目的是检测盾构隧道实际轴线与设计轴线之间的偏差，中心轴线三维坐标测量方法如下:

2.1 轴线中心平面位置测量

平面位置测量采用全站仪进行，测量时特制一根长度略短于管片直径的精制铝合金标尺，在标尺的中间位置固定安置测距棱镜和水准长气泡，将标杆横在洞门的下侧，并用水准气泡将其精密调至水平位置，将仪器置于地下导线点上，瞄准测距棱镜中心位置进行测量，分别测得其距离和夹角算出平面坐标，如图1所示。

式中x、y为轴线中心的坐标，x0、y0为架站点坐标，S为观测平距，α为测距视线的坐标方位角。

图1 轴线中心平面位置测量示意图

2.2 轴线中心高程测量

洞门中心高程测量采用电子水准仪进行测量。测量时，仪器设置在洞门中心附近的适当位置，后视地下高程控制点，读数为h，前视洞门中心附近位置并且固定仪器视准线，用一根长度 5 m的铝合金塔尺，分别直立于洞门的上、下壁，塔尺的一边严密与水准仪的竖直中丝。塔尺立于下壁采用正尺形式，读数为a;塔尺立于上壁采用倒尺形式，读数为b。即可测得洞门中心的高程，如图2所示。

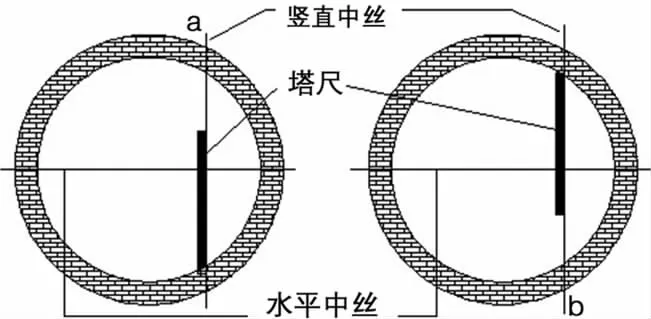
图2 轴线高程测量示意图

洞门中心的高程为:

HZX为洞门中心的高程，HO为地下高程控制的高程，h为后视标尺读数，a为前视正立标尺读数，b为前视倒挂标尺读数。

3 纠偏曲线设计及放样

3.1 纠偏曲线设计

盾构往前推进过程中会和设计路线差生偏差，当偏差量较小时，可以通过选择合适的管型和安装点位进行纠偏;当超过管片纠偏范围时，则需要设计纠偏曲线。纠偏曲线应尽可能的短，且纠偏起始方向和盾尾所在曲线相切，纠偏终点方向和设计路线相切。实际施工路线及设计轴线都是在三维坐标系统中，但是如果在三维情况下直接考虑曲线纠偏将加大纠偏难度，使问题复杂化。若对平面线形和纵面线形分别讨论，则数学模型将简化许多。

纠偏曲线起始于最近一环已拼装管环，经过盾构机，切向返回设计轴线。纠偏示意图如3图所示。

图3 纠偏示意图

传统的纠偏曲线通常三次抛物线，数学模型为:

式中，x，y为盾构机纠偏曲线上的点的坐标，a，b，c，d为待求参数。根据隧道的设计模型列出纠偏曲线曲率半径的方程，以曲率半径取最小值时为最优条件，根据纠偏曲线与当前开挖曲线满足的几何关系为约束条件求出纠偏曲线的待定参数，这种方法往往难以列出约束条件方程，且求解过程复杂［5］。

本文提出一种使用连续反向圆曲线来设计纠偏曲线，并分析推导该模型的纠偏曲线参数的解算方程，如图4所示，直线MN是设计路线，AB是盾构机的当前位置，弧BCD是纠偏曲线，纠偏起点B所在的纠偏曲线方向和当前盾构机前进方向相切，纠偏终点D所在的纠偏曲线切线方向和设计路线相切，弧BC和CD是半径相同的圆曲线。本文提出的纠偏曲线模型中的半径是盾构机所能挖掘曲线的最小半径R，这样可以使纠偏曲线最短，最小半径R不仅和盾构机参数有关，也受路线设计要求即管片参数影响。

假设此时盾构机AB与设计路线MN的夹角为θ，水平偏差为m，即点B到直线MN的垂直距离为m，令第一段纠偏圆曲线的圆心角为α1，第二段纠偏圆曲线的圆心角为α2，如图4所示，纠偏圆曲线的作用一方面要纠正盾构机的方向，另一方面要纠正水平偏差，根据这两个条件列方程求解纠偏曲线参数α1和α2，用求出来的圆心角乘以半径R即可得到纠偏曲线的长度l。

图4 纠偏曲线解算示意图

由图4和平面解析几何知，圆曲线CD在点C出的切线和MN的夹角为α2，其和圆曲线BC在点C处的切线和过点E的水平线的夹角相等，即:

由圆曲线CD的参数计算点C到直线MN的距离d为:

同理由圆曲线BC的参数和AB起始数据计算距离d为:联立式(4)和式(5)并整理得:

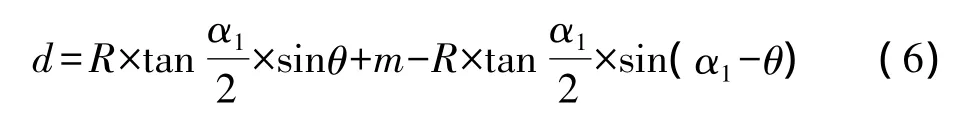
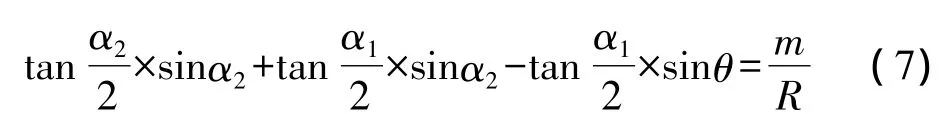
式(4)和式(7)可组成二元一次方程组，解该方程组即可求得纠偏曲线特征参数α1和α2，由下式即可求得纠偏曲线的长度l:

3.2 纠偏曲线放样

如图5所示，纠偏圆曲线相关曲线要素在图中已标明，其中ZY到JD的方位角用θ1表示，JD到YZ的方位角用θ2表示，且ZY点即为纠偏曲线的起点，根据纠偏曲线设计的结果可知半径R、弧长L及圆心角α等3个参数，依据盾构机当前姿态可知ZY点坐标及θ1的值。令纠偏曲线上待放样的点与ZY点距离为li。

图5 圆曲线示意图

(1)当0＜li≤L/2，以 ZY 点为原点 O，以 ZY 点至JD点的方向为x轴正向建立左手坐标系xoy(切线支距法)。如果待放样点至ZY点的弧长为li，那么其在xoy中的坐标可由以下公式求得:

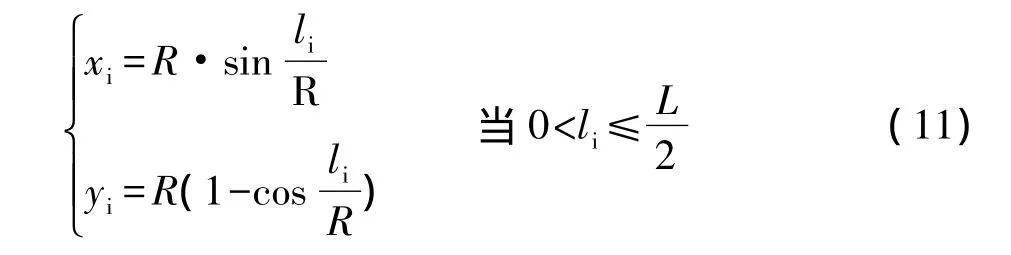
然后再代入下面的坐标转换公式中可求得放样点在工程坐标系中的坐标:

(2)当L/2＜li≤L时，以YZ点为原点，以YZ点至JD点的方向为x轴正向建立左手坐标系xoy。如果待放样点至ZY点的弧长为li，那么其在xoy中的坐标可由以下公式求得:

然后再代入下面的坐标转换公式:

4 结语

地铁隧道施工环境复杂，测量条件差，盾构轴线的控制主要通过提高仪器精度、增加测量频率、采用不同的测量方法以及改善施工工艺等途径来确保开挖方向的精度及可靠性。引起盾构轴线偏移的主要原因有:①盾构前进遇到的阻力不均衡。②盾构制作安装误差。③管片的拼装质量较差。④测量精度不高。

一旦出现偏差过大的情况，就得设计纠偏曲线，传统的纠偏曲线计算复杂，难以控制盾构机沿纠偏曲线推进，本文提出的连续反向圆曲线的方法可在一定程度较少计算工作量，易于控制盾构机前进。在盾构掘进过程中必须精心测量，对每一环都必须提交切口、盾尾高程及平面偏差实测结果，并由此计算出盾构姿态及成环隧道中心轴线与设计轴线的偏差，将测量的成果绘制成隧道施工轴线与设计轴线偏差图，发现有偏离轴线的趋势，应及时采取合理的纠偏方式来连续、缓慢的纠偏，使盾构掘进轴线与隧道设计轴线相一致，达到相应的施工技术要求。

［1］王智．地铁盾构姿态自动测量系统的研究与实现［D］．上海:同济大学，2011．

［2］ 高春香．盾构施工中管片拟合DTA问题研究［D］．武汉:华中科技大学，2004．

［3］金剑锋，王智．罗德里格矩阵在盾构引导系统中的应用研究［J］．城市轨道交通研究，2011，14(3):42～44．

［4］陈平．盾构推进轴线控制技术［J］．检测试验与测量，2006，6(1):107 ～110．

［5］张厚美，古力．盾构机姿态参数的测量及计算方法研究［J］．现代隧道技术，2004，41(2):14～20．