无人机光束法空三稀疏矩阵处理与实现
2014-02-08亓晨赵西安董友强陈柯
亓晨 ,赵西安,董友强,陈柯
(1.北京建筑大学测绘与城市空间信息学院,北京 100044;2.北京灵图软件技术有限公司,北京 100193)
1 引言
无人机航测具有高机动性、灵活性、使用成本低等特点,在航测领域得到越来越广泛的应用[1~3]。然而无人机航测与传统航测相比具有以下不足:无人机影像像幅小,数量多,信息采集量大,后期在光束法空三平差中需要处理大量的数据,致使误差方程系数矩阵规模庞大,可达几万阶或几十万阶;无人机飞行姿态不稳定,倾角过大,影像重叠部分不规则,畸变明显,严重影响数据质量,致使光束法空三平差中出现接近奇异的病态方阵,此类矩阵无法求逆或求逆结果非常不准确,影响平差结果的稳定性。因此,如何高效利用有限的计算机内存完成如此大规模稀疏矩阵的存储和运算以及对病态矩阵的避免,保证运算的稳定性,值得我们探讨和研究。对稀疏矩阵的压缩存储有多种方案,较常用的有对角线存储法,对称矩阵的变带宽存储法,CSR存储法,坐标存储法,Ellpack-Itpack存储法等[4~6]。经研究发现,上述技术虽然能够解决多数大规模稀疏矩阵的存储和解算问题,却不能针对光束法平差系数矩阵的独特结构直接使用。提高光束法空三平差稳定性的措施,多数集中在对病态方程的解算方面,如岭估计法、截断奇异值法和正则化方法等[7~8],却忽略了对平差前期对病态矩阵的避免。对于无人机光束法空三平差,内存管理、矩阵解算技术以及对病态矩阵的避免,对于实现其解的高效性和稳定性都极为重要。
2 无人机光束法空三平差
2.1 光束法空三平差模型
光束法空三平差的基本数学模型是共线方程:
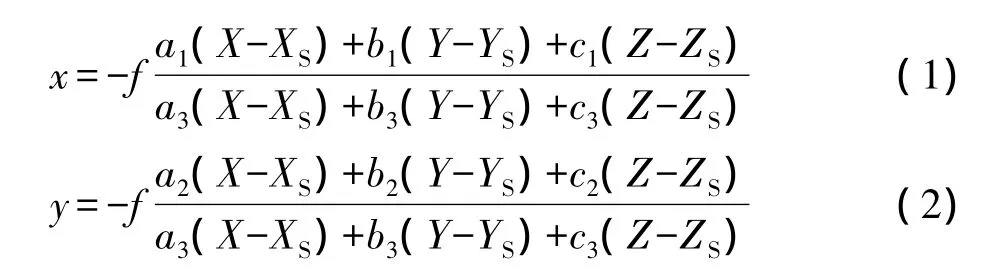
对上式进行线性化,可得到误差方程式,写成矩阵的形式为:

在式(3)这类误差方程式中含有两类未知数:外方位元素t和加密点的地面摄影测量坐标X。相应的法方程式为:

消去未知数X后,可得改化法方程式:
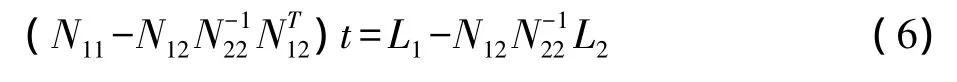
对改化法方程式(6)采用循环分块法求出全区每片的外方位元素,然后采用前方交会法求出加密点的地面坐标[9]。
2.2 光束法空三平差存在问题
光束法空三平差具有严密的理论基础,是目前空三解算最常用的方法。但无人机航测的大数据量会导致误差方程系数矩阵规模庞大,且矩阵规模随着测区大小和像点数量的增加而增加。如果一个区域网由7航带,每航带50张影像组成,每像对匹配得到300对同名像点,地面点数量为 40 000左右,那么误差方程式的数量至少为300×50×7×2=210 000,相应的误差方程系数矩阵则是一个数十万阶的大规模稀疏矩阵。对这样一个矩阵的存储,计算机内存显然是不够的,需要我们针对矩阵的特点,进行有序分块存储。
光束法空三平差需要通过参数消去法将法方程式(5)转换为改化法方程式(6),这个过程中需要对N22求逆,得到。而在无人机航测数据质量不好的情况下,方阵N22的行列式值几乎为零,接近奇异,呈现病态,无法求逆或求逆结果非常不准确[10],影响解算的精度和稳定性。因此需要对N22的结构深入剖析,从而采取措施避免病态。
3 大规模稀疏矩阵处理
3.1 大规模稀疏矩阵内存管理
本文根据无人机光束法空三平差中遇到的大规模稀疏矩阵的特点,设计了一种内存管理方法。下面用一个实例来详细介绍这种内存管理方法。
现在有一个由2条航带,每航带3张影像组成的区域,如图1所示。
首先,将所有像片进行编号,除第1航带,每航带接由上一航带像片编号依次增加,就本例而言,所有像片依次编号为 1,2,3,4,5,6。依次按照像片顺序,每像片所包含的像点顺序,列出误差方程式,该误差方程式系数矩阵结构如图2所示:

图1 区域网点位分布图

图2 误差方程系数矩阵结构
(1)对于系数矩阵A的存储:
将A定义为一个4维数组,首先以像片为单位将A 分为 A1,A2,A3,A4,A5,A6。假设第 i像片中有 n 个像点,则将Ai按像点点号大小依次分为Ai1,…,Ain,则Aik(1≤k≤m)表示第i像片上的第k个像点所列误差方程系数矩阵中的A矩阵。
对于A的转置AT的存储:


此外,对于AT的存储,还要考虑光束法空三平差的特点以及法方程式(5)中N12的求解。光束法空三平差中的未知参数分为像片的外方位元素与加密点坐标两类,但不包含控制点坐标,对控制点所列误差方程式系数矩阵中的B为零矩阵,致使N12=AT·B的求解过程中与控制点对应的N12全为零矩阵,所以可以认为与控制点对应的AT并未参与N12的解算。因此为了N12的解算方便,需对AT进行另外一种方式的存储,使得AT中不包含控制点对应的AT。将按该方式存储的AT记为(A_E)T,下面给出(A_E)T的存储方式:

(2)对于系数矩阵B的存储:
针对上文提到的光束法空三平差的特点,为了解算方便,对B进行分块存储时,也不再考虑控制点。将B定义为一个四维数组,首先以像片为单位将B分为B1,B2,B3,B4,B5,B6。假设第 i像片有 m 个像点(非控制点),则将Bi按像点点号大小依次分为Bi1,…,Bim,Bik(1≤k≤m)则代表第i像片中第k个像点(非控制点)所列误差方程系数矩阵中的B矩阵。
对于系数矩阵BT的存储:
将BT定义为一个四维数组,等同于对B的处理,假设第i像片有m个像点(非控制点),则将按像点点号大小依次分为(1≤k≤m)则代表第i像片中第k个像点所列误差方程系数矩阵中B矩阵的转置BT。
法方程式系数矩阵结构如图3所示:

图3 法方程式系数矩阵结构
(3)对于N11的存储:
由图可知,N11是由6个6×6的方阵沿对角线排列组成的对角方阵(图中左上角6个黑色方块)。将N11定义为一个三维数组,依次按像片顺序将N11分为N(11)1,N(11)2,N(11)3,N(11)4,N(11)5,N(11)6,分别对应6 个方阵。
(4)对于N12的存储:
由图可知,N12的基本单位是6×3的小矩阵。将N12定义为一个四维数组,按像片顺序将N12依次分为N(12)1,N(12)2,N(12)3,N(12)4,N(12)5,N(12)6。假设第 i像片有m个像点(非控制点),则按照该像片像点序号依次分为 N(12)i1,…,N(12)im,N(12)ik(1≤k≤m)表示第 i像片中第k个像点(非控制点)对应的6×3的矩阵ATB。
等同于对N12的处理,只是基本单位是转置关系,记为。
(6)对于N22的存储:
由图可知,N22是由若干3×3的方阵对角排列组成的对角方阵,每个小方阵与区域网中每个加密点是一一对应的关系。将N22定义为一个三维数组,数组中每个元素表示区域网中每个加密点对应的3×3方阵,假设某点是区域网所有待定点中第k个点,则该点对应的小方阵记为N(22)k。
由法方程式(5)可得改化法方程式(6),改化法方程式的系数矩阵规模有限,且通常情况下,非零元素较少,故不属于大规模稀疏矩阵,所以这里不需讨论。
3.2 大规模稀疏矩阵算法
对于大规模稀疏矩阵已经实现分块存储,对于方程式的解算,普通的矩阵运算方法已不适合,需要设计一套适用于上述矩阵分块存储方式的矩阵运算方法。这里重点讨论两个过程:由误差方程系数矩阵得到法方程系数矩阵的过程以及由法方程系数矩阵得到改化法方程式系数矩阵的过程。
首先给出由误差方程系数矩阵A和B得到法方程系数矩阵 N11,N12,,N22的矩阵运算方法。
(1)N11的解求方法:
由N11的存储方法可知,N11的基本单位是对应第i像片的6×6的方阵N(11)i,所以这里只需讨论对于N(11)i的解算方法。假设第i像片有n个像点,则:

(2)N12的解求方法:
由N12的存储方法可知,N12的基本单位是对应第i像片中第k个像点(非控制点)的6×3的矩阵N(12)ik,所以这里只需讨论对于N(12)ik的解算方法。假设第i像片中某点是第k个像点(非控制点),则:

在求得N12以后,将N12的基本单位转置便可得到。
(4)N22的解求方法:
由N22的存储方法可知,N22的基本单位是与区域网中第k个加密点(非控制点)对应的3×3的方阵N(22)k,所以这里只需讨论N(22)k的解算方法。首先,需要通过遍历像点数据得到包含该像点(非控制点)的像片数n以及每张像片中该像点对应的误差方程的系数矩阵B,依次记为B1,B2,…,Bn,则
在法方程系数矩阵全部解求完毕之后,需要由法方程系数矩阵解求改化法方程式的系数矩阵N11-N12,为表达简便,暂且将 N12简记为 NN,将 N11-N12简记为 N。
(5)NN的解求方法:
易知,NN是一个36×36的方阵,由36个6×6的方阵组成,将每个方阵看作一个元素,NN便简化为一个6×6的二维数组,解求NN的任务即简化为计算NN中的36个元素,记NN中第i行第j列的元素为NNij。首先,找到第i像片与第j像片的所有公共点,记作p1,p2,…,pn(假设有 n 个公共点),pk(1≤k≤n)在第 i像片所有非控制点中的序号记作pki,在第j像片所有非控制点中的序号记作pkj,则:
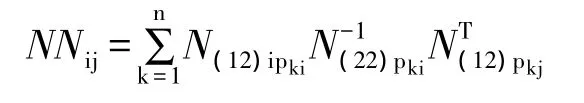
(6)N的解求方法:
将NN中对角线上6×6的方阵NN11,…,NN66依次作 NNii-N(11)i(i=1,2,…,6)的处理,再将此时的 NN取反,便得到改化法方程式系数矩阵N。
3.3 矩阵运算稳定性分析
对N22进行结构剖析,由图3可知,N22是由11个三阶方阵对角排列组成的稀疏矩阵,因而对其求逆等同于对各个三阶方阵求逆。在数据不好的情况下,个别三阶方阵的对应的行列式值几乎为零,接近奇异,导致无法求逆或求逆结果非常不准确[10],N22就会呈现病态,导致平差精度下降,结果不稳定。
由3.1中所提N22的存储方式可知,N22中每个三阶方阵与区域网中每个加密点是一一对应的关系。为了避免N22呈现病态,只需将其中病态的三阶方阵所对应的加密点剔除即可。采用的方法是,在列出误差方程式之前,求出每个加密点在N22中对应三阶方阵的行列式值,将行列式值的绝对值小于0.1的三阶方阵对应的待定点直接由原始像点数据中剔除。如此一来,避免了方阵N22会出现病态的情况,保证了平差解算的精度和稳定性。
4 无人机光束法空三平差实现
4.1 内存管理实现
内存管理的实现,主要体现在方程系数矩阵的VC++内存设置管理。3.1中所述各矩阵VC++内存管理方法相同,其实现程序如下。
稀疏矩阵内存管理实现程序:

4.2 矩阵运算稳定性实现
以下为矩阵运算稳定性实现方法:

说明:①PhotoN为所有航带像片的总数;②PointN是一维数组,PointN[i]表示第i张像片包含的像点数;③ExPointN是一维数组,ExPointN[i]表示第i张像片包含的非控制点像点数;④SPointN是整个区域网中加密点的个数。⑤ClmofB是一个二维数组,ClmofB[i][j]表示第i像片中第j个非控制点像点对应的加密点在区域网所有加密点中的序号。⑥Calculating()是一个用于求解N22的函数。⑦valueHLS()是一个用于求解N22行列式值的函数。⑧SickPoint是一个一维数组,存储需要剔除的加密点的序号。⑨PointData是一个vector数组,用于存储每个像点的像平面坐标x、y和对应的地面摄影测量坐标 X、Y、Z,如 PointData[i][j].x表示第i像片第j个像点的像平面坐标x。
5 实验与分析
本次无人机实验数据采集区域为新疆沙尔拜客水电站坝区,地形平坦,以农田为主,包含河流及少量民房。无人机所携带数码相机型号为JC4,焦距 24 mm,影像分辨率为 3888 xs×2592 xs,CCD尺寸 22.2 mm×14.8 mm。测区含有7个航带,每航带像片数在45~50之间,数据采集基本信息如表1所示:

数据采集基本信息 表1
本实验数据含有12个地面控制点,控制点在高斯坐标系下的高斯平面坐标如表2所示:

控制点的高斯平面坐标 表2
为了检查解算精度,将其中CP_03,CP_06,CP_09,CP_11这4个控制点作为检查点。光束法空三平差解算的数据及解算情况如表3所示:

光束法空三平差数据及解算 表3
由表3可知,实验数据量巨大,如果在光束法平差过程中不对稀疏矩阵进行处理,是不可能完成解算的。而采用本文所述算法,不仅使解算变为可能,还保证了较快的收敛速度及较高的稳定性,节省了计算机内存。
表4是本次光束法空三平差实验的控制点精度报告,表5是检查点的精度报告:

控制点精度 表4

检查点精度 表5
由以上两表明显可以看出,采用本文所述算法进行无人机光束法空三平差,精度远远高于 1∶2 000的测图要求。
6 结论与展望
本文提出了针对无人机光束法空三大规模稀疏矩阵的一种内存管理与解算方法并加以实现。通过对稀疏矩阵进行分块存储与运算以及部分加密点的剔除,达到了只对稀疏矩阵的非零元素进行存储的目的。有效降低了无人机光束法空三解算过程中对计算机内存的消耗,提高了运算效率,减少了运算时间,同时避免了病态矩阵的出现,保证了解算结果的稳定性。最后,通过对无人机实验数据进行测试,验证了该方法的可行性与高效性,平差的精度也符合要求。但由精度报告也可看到,高程精度总体要低于平面精度,同时稳定性也较差。今后将会就如何改善无人机光束法空三的高程精度及稳定性作相应研究并加以实现。
[1]鲁恒,李永树,何敬等.无人机低空遥感影像数据的获取与处理[J].测绘工程,2011(1):51~54.
[2]Laliberte A S,Rango A.Texture and Scale in Object-based Analysis of Subdecimeter Resolution Unmanned Aerial Vehicle(UAV)Imagery[J].Geoscience and Remote Sensing,2009,761 ~769.
[3]Laliberte A S,Herrick J E,Rango A,et al.Acquisition,or Thorectification,and Object- based Classification of Unmanned Aerial Vehicle(UAV)Imagery for Rangeland Monitoring[J].Photogrammetric Engineering & Remote Sensing,2010,661 ~672.
[4]Ichitaro Yamazaki,Richard,Scalettar.A High-Quality Preconditioning Technique for Multi-Length-Scale Symmetric Positive Definite Linear Systems[J].Numerical Mathematics:Theory,Methods and Applications,2009,469 ~484.
[5]A sparse matrix model-based optical proximity correction algorithm with model-based mapping between segments and control sites[J].Journal of Zhejiang University-Science C(Computers& Electronics),2011,436~442.
[6]Yi-zhou HE,Xi CHEN,Hao Wang.Modeling correlated samples via sparse matrix Gaussian graphical models[J].Journal of Zhejiang University-Science C(Computers& E-lectronics),2013,107 ~117.
[7]吴杰,李明峰,余腾.测量数据处理中病态矩阵和正则化方法[J].大地测量与地球动力学,2010(04):102~105.
[8]N.S.Mera,L.Elliott,D.B.Ingham.On the use of genetic algorithms for solving ill-posed problems[J].Inverse Problems in Engineering,2003,105 ~121.
[9] 李德仁,郑肇葆.解析摄影测量学[M].北京:测绘出版社,1992:161~166.
[10] 同济大学应用数学系.线性代数[M].北京:高等教育出版社,2003:43.
