基于匹配追踪的脑磁图体感诱发信号提取方法

2014-02-07严汉民

中国医学装备 2014年5期

郭洁严汉民*

郭洁①严汉民①*

目的：利用匹配追踪(MP)算法的良好参数化描述特性，研究癫痫脑磁图的时频分布特征。方法：提出应用MP算法提取体感诱发磁场(SEF)信号的详细的时频成分。结果：对多例正常受试者的体感诱发脑磁图信号进行时频分析，从中提出大部分信号中都存在的时频成分，表明系列稳定的SEF时频成分可使用MP分解算法识别。结论：体感诱发信号通过MP分解，能够产生稳定和微小的时频成分，并且这些成分在时频中具有特定的位置，从而为临床脑功能和脑部疾患发病机制的研究提供可靠的研究指标。

脑磁图；体感诱发磁场；短时傅里叶变换；匹配追踪

郭洁，女，(1984- )，硕士研究生。首都医科大学宣武医院医学工程科，研究方向：医学信号处理。

高频振荡信号的有效采集和提取是高频振荡研究的基本前提。大脑皮层的电活动信息主要通过头皮脑电图、皮层脑电图和脑磁图来采集。无创采集的脑磁图信号具有高时间分辨率，并能够提供全脑电活动的信息的优点，因此在大脑功能的研究中得到了越来越多的应用，通过分析脑磁图信号，能够提供更多的高频振荡信息。

体感诱发磁场(somatosensory evoked magnetic fields，SEF)是经脑磁图设备记录刺激后的大脑皮质电磁反应。由于SEF幅度极小，而且常和一些伪差混淆在一起，常规的信号处理方法往往会导致信号的变形和信息的丢失。虽然短时傅里叶变换(short time Fourier transform，STFT)被广泛应用于信号的时频分析中，但由于STFT的频率分辨率与分析窗函数h(t)的有限带宽成正比，在时间分辨率和频率分辨率之间需要折衷。由于Heisenberg测不准原理，两者不可能同时满足。

信号的稀疏表达是近年发展起来的信号处理方法，将其应用到高频成分的提取中是稀疏表达算法的重要研究方向。其基本思想是从非常大的冗余字典中分解出一系列信号的时频成分。通过自适应逼近，MP算法可以提供比小波分析等方法更高的时频分辨率。

1 实验数据与方法

本研究使用的脑磁图数据由首都医科大学宣武医院脑磁图室提供。

(1)数据采集设备：芬兰Elekta Neuromag 306导脑磁图仪。

(2)数据特性：采样频率1000 Hz，滤波带通0.1～330 Hz。

(3)试验对象：在校大学生志愿者，无神经系统疾病历史，无特殊医疗状态。

(4)数据预处理：使用Neuromag系统自带的MaxFilter软件，采用信号空间分割(signal space separation，SSP)算法对数据进行预处理，提高信号的空间分辨率和信噪比。

1.1 数据采集

数据采集前受试志愿者明确其任务。数据采集时志愿者平躺于磁屏蔽室内，双侧前臂腕部经皮肤正中神经分别给予相同电刺激；记录刺激后MEG数据100 ms，采集到的每段刺激信号包括X、Y方向的磁场计数据和N方向的梯度计数据，每个方向有102×100个数据。

1.2 数据分析

脑磁图的探测主机由204个磁场计和102个梯度计组成多信道探测阵列，所有信道可同时测量。磁场计线圈的优点是能够最大限度地保留信号强度，不引起信号失真；其弱点是对环境噪声无削减作用。梯度计测量的实际上是两个线圈对信号感应的差别，其优势是对环境噪声有一定的抑制作用。但同时梯度计也会削减信号。在本研究中为保留信号强度，主要分析磁场计信道采集到的数据。

由脑磁图信号可知，体感诱发后的异常信号主要出现在双侧颞叶区和顶叶区。因此，数据处理中主要分析颞叶和顶叶对应信道所采集到的数据，其数据处理采用如下步骤。

(1)STFT。由于脑磁图信号属于时变非平稳信号，其频率特性随时间的变化而变化，简单的傅里叶变换不能准确反映脑磁图信号随时间变化的频谱特性，因此，通过对信号进行STFT获得脑磁图信号的时频特性，其基本原理如公式1：

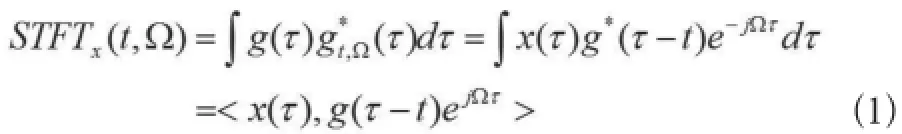
式中，x(τ)为待处理信号，g(τ)为窗函数，对窗函数截下来的局部信号做傅里叶变换，即得到t时刻该段信号的傅里叶变换。不断移动t，即不断地移动窗函数g(τ)的中间位置，可得到不同时刻的傅里叶变换。

(2)MP分解。给定一个离散时间信号X(n)，MP分解将信号X(n)为基本功能的一个线性组合{G0，G1，……Gn-1}，从一个非常大的冗余字典D中描述的定义参数如公式2：

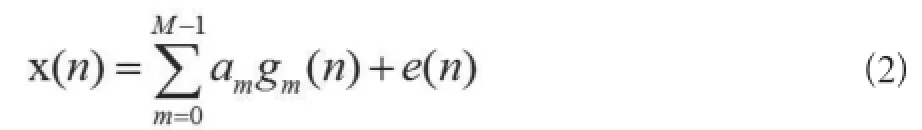
式中，m为分解时频分量的数目，am为系数，e(n)是m-时频组件，X(n)为分解的残留物。注意，在MP算法中信号的时频分量以在字典中定义的函数来表示。

尽管X(n)完全可以用正交函数如三角函数来估计，但仍对稀疏逼近感兴趣。因其目标是从冗余词典D中自适应地选择有限数量(m)的基本波形的功能，能够解释的信号时频特征残差矢量的范数(N)在公式(2)被最小化时得到最优稀疏逼近信号X(n)，通常是由一个迭代算法实现，如公式3、公式4：

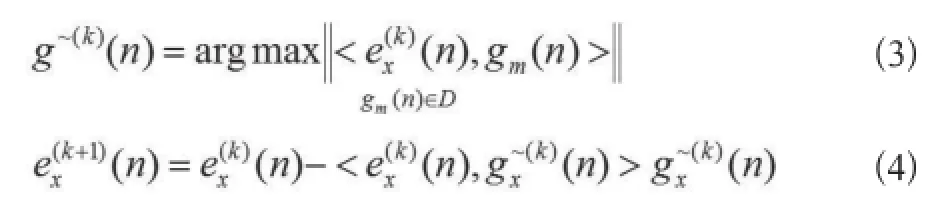
从过完备字典D中找出和信号X(n)具有最高内积的g～(0)(n)，这意味着它占的信号能量最大，形成主要的时频成分a(0)g～(0)=＜g～(0)(n)，e0(n)＞g～(0)(n)，然后残余成分由公式(4)得到，g～(1)(n)通过公式(3)得到。执行两个步骤迭代，直到达到一定的停止准则。

本实验采用Gabor字典，是因其具有很好的时频局部化特征。Gabor函数表示如公式5：

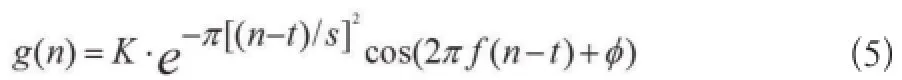
2 实验结果分析

由受试者的导联分布图反映出当给予左侧刺激时，右侧信道有明显的棘波信号。在信号分析中主要对比了左侧67号信道与右侧84号信道，左侧13号信道与右侧40号信道，左侧7号信道与右侧50号信道。

从所有脑磁图刺激数据中任取一组刺激，分析右侧50号信道的MEG信号数据。正常受试者的体感诱发MEG信号(如图1所示)；7点和15点汉明窗STFT的体感诱发MEG信号(如图2、图3所示)。图2显示，较小的汉明窗能够获得较高的时间分辨率，但要以降低频率分辨率为代价，反之亦然。

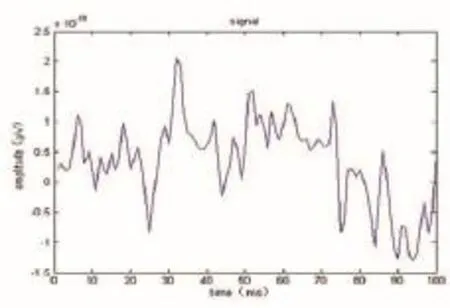
图1 受试者体感诱发MEG信号

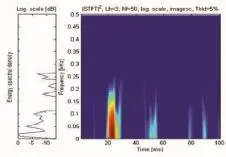
图2 7点汉明窗STFT

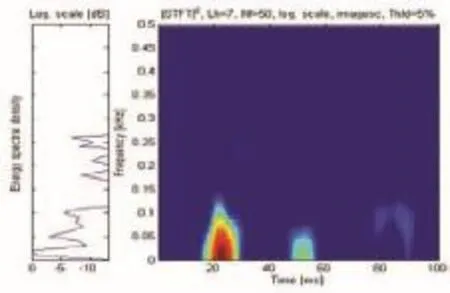
图3 15点汉明窗STFT

如图4(a)所示，采样点为100个，采样频率为1000 Hz，经过6次迭代，稀疏分解得到一个包含6个非零值的解向量和6个与非零值一一对应的原则，图4(b)是6个原子的重构脑磁图信号，虽然相对于长度为100的原信号解向量非常稀疏，但重构脑磁图信号在轮廓上依然非常接近于原信号，几乎囊括了脑磁图体感诱发后的所有高频震荡信息。继续进行MP分解，用更多的原子表示脑磁图信号能进一步减小误差。

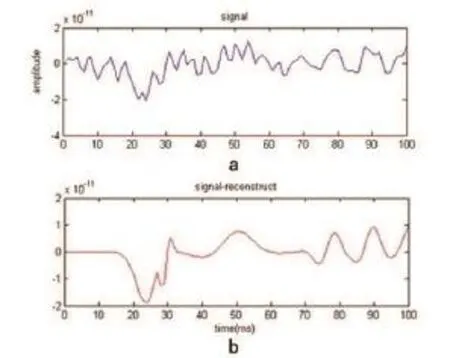
图4 脑磁图信号的MP分解

如图5所示，图5(b)为迭代45次得到的重构信号，与原信号图5(a)相比误差＜5%。

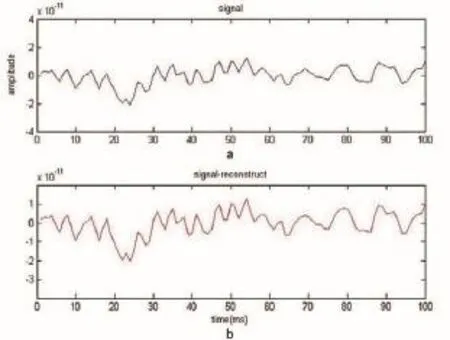
图5 脑磁图信号的MP分解及信号重构

为进一步提取脑磁图高频震荡信息，进一步通过MP方法从图1的信号中提取分解出来6组时频分量(如图6所示)。

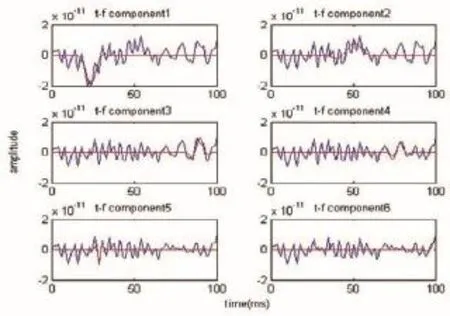
图6 MP分解图

如图7所示，6类最高能量时频分量及其参数，红色线表示Gabor组件，蓝色线表示上次迭代分解的残留物。

结果显示，SEF信号通过MP分解能够产生一套稳定和微小的时频成分(图7a-f)，各个时频成分出现的次序及时间约为：a(18～35 ms)、e(28～44 ms)、b(45～63 ms)、d(65～78 ms)、c(76～90 ms)、f(88～100 ms)。这一结果与STFT分析的结果相一致。

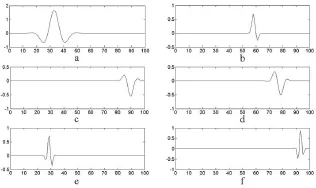
图7 6类SEF信号典型波形

本研究继续验证右侧84号信道和40号信道，结果验证了这一结论。试验共分析了同一被试者右侧60组实验数据，统计后各成分出现的次数及相关信息见表1。

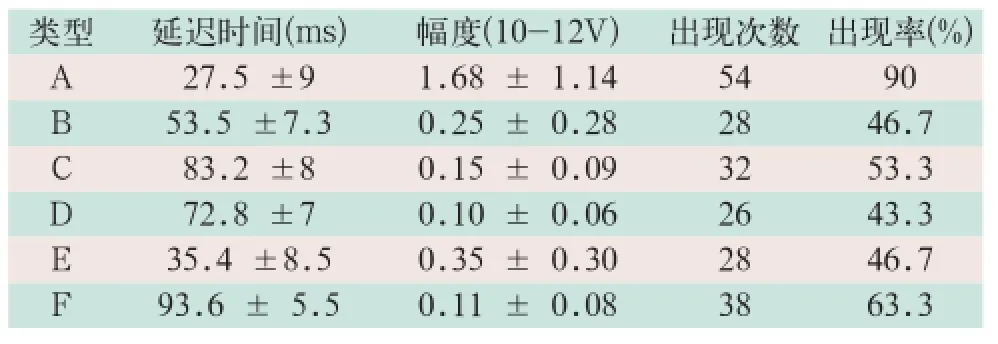
表1 传统屏片系统与数字化系统对比

继续取不同被试者进行样本分析，经验证同样存在稳定的时-频成分。

3 讨论

本研究采用了MP算法，在Gabor函数的形式，由5个参数定义，对脑磁图SEF信号分解成一系列时频成分。研究中发现6类稳定的SEF时频成分，如图7所示。经过对同一名受试志愿者的多次试验表明，SEF主要时频分量在个体中是明确而肯定的，其同时也被其他时频分析方法如STFT验证。

对于MP算法，本研究采用Gabor函数为基本成分，高斯函数经过伸缩、位移、频率调制组成的Gabor字典，包含许多特征的基，具有良好的时频特性，能够保证信号稀疏表达的准确性。然而，Gabor函数不能很好地描述与随时间频率变化或不对称的包迹的组件。其他复杂的词典，如Chirplet字典可被用在MP分解中，但需以增加计算负荷为代价。因此，构造更高精度更简运算的过完备字典，依然是今后信号处理的关键问题。

4 结论

本研究显示，电刺激腕部正中神经后脑的初级体感反应的峰值主要在20 ms、35 ms及60 ms出现。本研究确定了一系列稳定的SEF时频分量，传递了脑磁图SEF重要的瞬时高频信息。将刺激所得脑磁图信号通过MP方法分解为多个时频分量，所得到的时频分量可能有助于理解脑磁图复杂的反应模式和生理根源，从而为临床脑功能和脑部疾患发病机制的研究的病灶的定位提供一个可靠的研究指标。

[1]Vinje WE.Gallant JL.Sparse coding and decorrelation in primaryVisual cortex during naturalVision[J].Science，2000，287(5456)：1273-1276.

[2]Olshansen BA.Field DJ.Emergency of simplecell receptive field properties by learning a sparse coding for natural images[J].Nature，1996，381(6583)：607-609.

[3]Mallat SG，Zhang ZF.Matching pursuits with time frequency dictionaries[J].IEEE Transactions on Signal Processing，1993，41(12)：3397-3415.

[4]Davis GM，Mallat SG，Zhang ZF.Adaptive timefrequency decompositions[J].SPIE J Optical Engi neering，1994，33(7)：2183-2191.

[5]Chen SS，Donoho DL，Saunders MA.Atomic decomposition by basis pursuit[J].SIAM Journal ofScientific Computing，1999，200(1)：33-61.

[6]Gorodnitsky IF，Rao BD.Sparsesignal reconstruction from limimd data using FOCUSS：axe-weighted minimum norm algorithm[J].IEEE Transactions 012 sjgnal Processing，1997，45(3)：600-616.

[7]Figueiredo MAT，Nowak RD，Wright SJ.Gradient projection for sparse reconstruction：application to compressed sensing and other inverse problems[J].IEEE Journal of Selected Topics in Signal Processing，2007，1(4)：586-598.

[8]Mancera L，Portilla J.1_n-norm-based sparse representation through alternate projections[C]. USA：Proceedings of IEEE In-ternational Conference on Image Processing Washington DC，2006：2089-2092.

[9]Bergeau F，Malt S.Match pursuit of images. In：Proceedings of the 1995 International Conference on Image Processing[C].USA：Washington DC，IEEE，1995：53.

[10]Ventura RF，Vandergheyust P，Frossard P.Lowrate and flexible image coding with redundant representations[J].IEEE Transactions on Image Processing，2006，15(3)：726-739.

[11]Meyer Y.Osillating patterns in image processing and nonlinear evolution equation[C]. Boston：American Mathematical Society，2001：122.

[12]校午阳，郑旭媛.基于匹配追踪的癫痫脑电信号的时频分析[J].国际生物医学工程杂志，2012，35(1)：8-13，17.

[13]孙吉林，尹领，赵文清.脑磁图[M].北京：科学技术文献出版社，2002：10-13.

[14]柳渊，孙伟，严汉民，等.癫痫患者脑磁图的高频震荡量化算法研究[J].中国医学装备，2012，9(11)：1-3.

Extraction method of the magnetoencephalography somatosensory evoked signals based on the MP decomposition

GUO Jie, YAN Han-min// China Medical Equipment,2014,11(5):48-51.

Objective:Matching pursuit algorithm(MAP),for its good parametric characterization, is applied in Magnetoencephalography(MEG) to study time-frequency distribution. Methods: This paper proposes to apply a high-resolution time-frequency analysis algorithm, the matching pursuit (MP), to extract detailed time-frequency components of SEF signals.Results:Experimental results on cortical SEF signals of several normal subjects show that a series of stable SEF time components can be identified using the MP decomposition algorithm.Conclusion:This study shows that there is a set of stable and minute time-frequency componentsin SEF signals, which are revealed by the MP decomposition. These stable SEF components have specific localizations in the time domain and may provide a reliable index for clinical research of brain function and brain disease pathogenesis.

Magnetoencephalography; Somatosensory evoked fields; Short time fourier transform; Matching pursuit

1672-8270(2014)05-0048-04

R741

10.3969/J.ISSN.1672-8270.2014.05.018