基于CFD的水下拖曳体艉部流场仿真
2014-02-07曾东李朋飞
曾东,李朋飞
武汉船舶通信研究所,湖北武汉430205
0 引 言
水下拖曳体是进行水下资源探测和海洋资源开发的重要载体,在军事和民用领域有着广泛的应用,如无人海洋资源探测、海洋环境调查、水下考古扫雷等,为了提高水下拖曳体的适装性,满足各种拖曳航速和应用环境,对水下拖曳体的性能提出了越来越高的要求。
优化水下拖曳体的外形,对于减小其形状阻力,进而减小拖缆的张力,提高拖曳航速有着积极的意义。因此,外形是水下拖曳体设计的重要组成部分,其主要包括以下两个方面:
1)拖曳体的外形设计[1];
2)拖曳体的结构设计与其有效载荷的合理配置。
在潜艇的优化设计方面,吴方良等[2]采用雷诺平均纳维—斯托克斯(RANS)方法计算潜艇三维粘性流场,分析了潜艇指挥台围壳对潜艇水动力性能的影响。张楠等[3]采用求解RANS 方程的数值计算方法,结合k-ε,RNG k-ε 与k-ω 这3 种湍流模型,预报了美国国防高级研究计划局(DAR⁃PA)潜艇模型SUBOFF 和CSSRC 潜艇模型SM-x的阻力与艉流场。李新汶等[4]认为艉部附体与艇主体的不同交接形式对艉部流场有较大影响,通过设计3 种不同交接形式,用理论计算求得各个流场分布,分析不同的连接形式对螺旋桨盘面处流场的影响,得出了与试验结果相吻合的结论。赵峰等[5]采用复杂流场多块耦合对潜艇含指挥台附体区域的周围粘性流场进行了计算。对由于指挥台围壳而造成的潜艇后体不均匀流场做了较成功的数值模拟,为潜艇后体流场及艉流场的试验研究和理论计算打下了良好的基础。本文旨在将潜艇指挥台围壳处流场的分析方法应用于水下拖曳体艉部流场的精细化分析,以此降低水下拖曳体的阻力,并提出优化的方向。
1 计算模型
在满足有效载荷搭载的条件下,水下拖曳体模型的外形及坐标系如图1 所示,取水下拖曳体中心线与头部的交点为原点,O0-x0y0z0为固定坐标系,O1-x1y1z1为连体坐标系。该模型是一个回转体,长度L=1.5 m,平行中体处直径为0.3 m。稳定翼距艏部端点0.52 m,艉部为NACA0020 翼型的十字尾翼,弦长为0.1 m,展长为0.4 m,最大厚度为0.012 m。该拖曳体在布局上分为艏部、艉部和中间舱段3 部分,其中艏部和中间舱段根据搭载的有效载荷可以适当进行调整。

图1 水下拖曳体模型示意图Fig.1 The underwater towed body
拖曳体模型置于数值水洞中,如图2 所示,水洞长为1.8L,直径为0.6L,拖曳体模型艏端点距水洞入流面0.5L,艉端点距水洞出流面0.3L。整个计算流域采用分区多块网格技术划分。为了较精确地模拟拖曳体边界层流场,在近壁区域用精细的六面体网格包住拖曳体,且在边界层上布置10~20 层网格,如图3 所示。

图2 计算域网格划分Fig.2 The grid of the computational domain

图3 拖曳体艉部网格示意图Fig.3 The grid of tail for the towed body
2 数学模型
2.1 控制方程
在流场非定常条件下,对于水下拖曳体粘性流场的计算,不可压缩流动控制采用时间平均,应用雷诺时均计算法则,不计密度脉动的影响,但是考虑平均密度的变化和拖曳体的体积力,其连续性方程与RANS 方程的张量形式为[6]:

2.2 湍流模型
由于RANS 方程不能封闭,所以需要选择湍流模式来使之封闭,本文采用k-ε 湍流模型,湍流动能k 方程为[6]

湍流耗散率ε 方程为

式中:Gk表示由平均速度梯度引起的湍动能;Gb为由浮力影响引起的湍动能;YM为可压缩湍流脉动膨胀对总耗散率的影响;αk和αε分别为湍动能k 和耗散率ε的有效湍流普朗特数的倒数;C1ε=1.44,C2ε=1.92,C3ε= 0.09。湍流粘性系数计算公式为

2.3 边界条件
为了更好地模拟无限流场的环境,在整个流域中,除了出口,其余两个边界均为速度入口。其边界条件为:u=U0,v=w=0 。其中:u 为轴向速度;湍流湍动能k 和湍动能耗散率ε 的初始值按下面的经验公式取值:取初始速度U0=2.5,1 m/s,出口处设置为自由出流,出口处边界条件沿流线方向有如下关系:,以拖曳体长为特征长度[7]。
拖曳体表面设置为固壁条件,物面边界条件满足无滑移条件,近壁区采取标准壁面函数修正,设外场速度为未受扰动的主流区速度U0。
3 计算结果
经过计算,静压力系数Cp沿拖曳体长度方向的分布如图4 所示。为便于对照,图中同时给出了文献[8]所得的计算和试验结果。从图中可以看出,在x=0 和x=0.91 处,Cp出现了峰值。x=0处是艏部最前端,沿x 方向流动的流体从此处开始绕流,速度为0,压力最大,压力系数也最大。在x=0.91 处出现较强的跳跃是因为翼的存在。Cp的变化趋势与文献[8]所得结果基本吻合。拖曳体不同速度下的阻力如图5 所示,从图中可以看出,在低速时计算结果与试验结果基本吻合,在速度较高时二者存在一定的差别,但是试验结果基本上能够验证计算结果的可靠性。

图4 静压力系数Cp沿长度方向分布图Fig.4 The coefficient of static pressure Cp along the length

图5 速度—阻力曲线图Fig.5 Variation of resistance with respect to velocity of the towed body
为精确计算低雷诺数下十字尾翼层流绕流,本文截取了计算模型网格艉部0.5 m 以后的部分,对尾翼前端的计算网格进行了重新分块。计算雷诺数Re 分别为1×105和2.5×105,特征长度为十字尾翼交接处的弦长,图6 所示为在截面y=0 上的速度分布。图7 所示为主体与十字尾翼交接处上游区的流线图。图8 所示为主体与十字尾翼交接处下游区形成的尾涡。由图7 和图8 可以看出,在尾翼交接处的上游区和下游区都出现了涡流,需要对交接处的线型进行适当的过渡,以减小尾涡的出现。图9 示出了雷诺数Re=2.5×105时的马蹄涡。从图中可以看出,马蹄涡在水下航行体和十字尾翼交接处的上游形成,并逐渐向下游发展。图10~图13 所示分别为截面x/L=0.91,0.93,0.96,0.98 的流线图。

图6 十字尾翼上游区交接处的速度分布(y=0)Fig.6 The velocity on the upstream region of junction at y=0

图7 十字尾翼上游区交接处的流线分布(y=0)Fig.7 The streamlines on the upstream region of junction at y=0
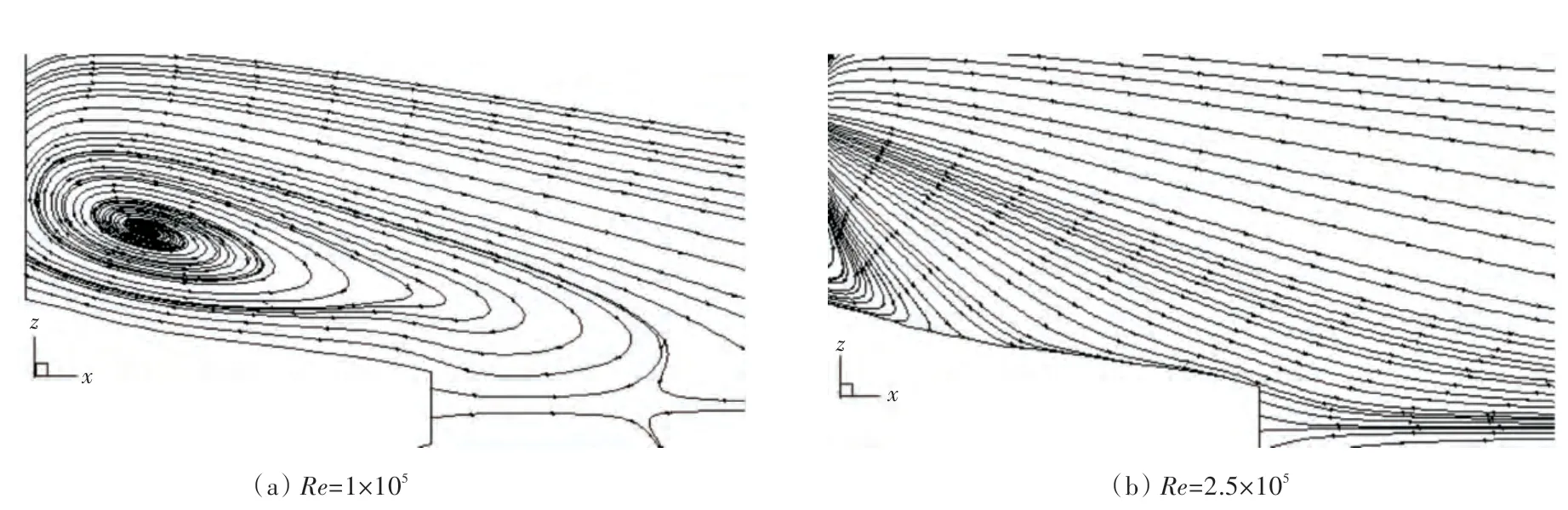
图8 十字尾翼下游角区的流线分布(y=0)Fig.8 The streamlines on the downstream region of junction at y=0

图9 马蹄涡形成和向下游发展(Re=2.5×105)Fig.9 The horseshoe vortex and the development to downstream(Re=2.5×105)
本文利用CFD 技术研究了水下拖曳体与尾翼交接处的流场速度分布。在计算雷诺数Re=1×105,2.5×105时可以看出,随着雷诺数的变大,在十字翼与水下拖曳体交接处上游区主流方向上形成了马蹄涡系,在下游区的涡流变化很大,随着雷诺数的变大,横向涡流也有明显的变化[9-10]。由图10~图13 可看出,在十字尾翼与拖曳体主体交接部位存在较大的涡流,需要在交接处进行过渡处理,以降低尾翼与主体的不平滑度,减小尾涡的出现。

图10 截面x/L=0.91 的流线图Fig.10 The streamlines on section x/L=0.91

图11 截面x/L=0.93 的流线图Fig.11 The streamlines on section x/L=0.93

图12 截面x/L=0.96 的流线图Fig.12 The streamlines on section x/L=0.96

图13 截面x/L=0.98 的流线图Fig.13 The streamlines on section x/L=0.98
4 结 语
本文以水下拖曳体为研究背景,对其艉部附体交界处的流场进行了分析,选取不同的雷诺数对流场进行了比较。通过流场分析,对水下拖曳体的艉部线型进行优化,对降低艉部流场的分离和减小阻力具有积极的意义,可为后续水下拖曳体的优化打下基础。同时,通过对艉部流场的分析,能够降低水下拖曳体的目标特征,提高其隐蔽性,为水下拖曳体外形设计提供优化的方向。
[1]周晗,谢海斌,徐海军,等.基于CFD 的水下机器人载体形体阻力优化设计[C]//2009 系统仿真技术及其应用学术会议论文集.安徽,合肥,2009:47-51.
[2]吴方良,吴晓光,马运义,等.潜艇指挥台围壳对阻力和伴流场影响数值研究[J].海洋工程,2009,27(3):91-99.WU Fangliang,WU Xiaoguang,MA yunyi,et al. The effect of submarine sail on the resistance and wake field[J]. The Ocean Engineering,2009,27(3):91-99.
[3]张楠,沈泓萃,姚惠之.潜艇阻力与流场的数值模拟与验证及艇型的数值优化研究[J]. 船舶力学,2005,9(1):1-13.ZHANG Nan,SHEN Hongcui,YAO huizhi. Valida⁃tion of numerical simulation on resistance and flow field of submarine and numerical optimization of sub⁃marine hull form[J].Journal of Ship Mechanics,2005,9(1):1-13.
[4]李新汶,陈源,王文琦.CFD 在潜艇艉附体与艇体连接形式研究中的应用[J].船舶力学,2003,7(5):28-32.LI Xinwen,CHEN Yuan,WANG Wenqi. Application of CFD to junction form of stern appendages[J]. Jour⁃nal of Ship Mechanics,2003,7(5):28-32.
[5]赵峰,周连第.潜艇含指挥台附体区域周围粘性流场的多块耦合计算[J].水动力学研究与进展(A 辑),1996,11(4):448-458.ZHAO Feng,ZHOU Liandi,Multiblock coupled com⁃putation of the viscous flow field around a submarine sail zone[J].Journal of hydrodynamics(Ser.A),1996,11(4):448-458.
[6]周俊杰,徐国权,张华俊.FLUENT 工程技术与实例分析[M].北京:中国水利水电出版社,2010.
[7]陈义良.湍流计算模型[M].合肥:中国科学技术大学出版社,1991.
[8]秦丽萍.水下航行器主体外形低阻低噪综合优化设计[D].西安:西北工业大学,2004.
[9]詹成胜,刘祖源,程细得.基于FLUENT 的潜艇水动力导数数值计算[C]//2007年船舶力学学术会议暨《船舶力学》创刊十周年纪念学术会议论文集.宁夏,银川,2007:119-127.
[10]王志博,姚惠之,张楠.指挥台围壳对潜艇尾流影响的计算研究[J].船舶力学,2009,13(2):196-202.WANG Zhibo,YAO Huizhi,ZHANG Nan. Calcula⁃tion and analysis of the effects of sail form on subma⁃rine wake[J]. Journal of Ship Mechanics,2009,13(2):196-202.
