一类混沌系统的电路设计及控制

雷腾飞，王清花

(1.西京学院 控制工程学院，西安 710123；2.新泰天宝一中，山东 新泰 271211)

自1963年 Lorenz 提出第一个混沌模型以来[1～3]，人们对混沌系统产生极大的兴趣.近几十年，混沌系统的构造一直被人们关注，不少学者提出以Lorenz系统为基础的若干变形的新混沌系统，如Chen系统[2]，Lü系统[3]，Liu系统[4]等[5～7].由于混沌理论在图像数据加密[8]、信号检测与处理[9]、机电控制系统[10]等方面的工程得到广泛应用.则构造新的简单混沌系统成为混沌应用研究的热点问题[4～7].

对初值的敏感性和长时间发展的不可预测性是混沌系统最显著的特点，混沌振荡产生危害在现实生活中随处可见，如何有效地抑制或消除混沌现象，已经引起全球众多学者的广泛关注. 1990 年 ， OttE等人提出了OGY方法;同年Pecora L M 提出了混沌同步思想.近年来 ，混沌同步的研究得到蓬勃发展，该研究方向迅速成为混沌控制领域的重要热点[7～11]．人们提出了多种混沌同步的思路和方法，比如状态反馈方法、变结构控制方法、自适应控制方法[11]、观测器方法[11]等 ，多数方法取得了良好的控制效果．但研究的系统大多数集中在以上几个系统及分数阶系统[10～11]，但对经典Lorenz系统稍微改变非线性项，即是一类复杂的混沌系统.

本文首先在Lorenz系统的基础上构造了一类新的混沌系统，对其通过数值仿真系统的吸引子图、分岔图以及Lyapunov指数研究了该系统的基本动力学特性；同时为了在实际中更好地应用此系统，设计系统的硬件电路并进行了仿真实验，进一步说明系统的客观存在性，最后利用 Lyapunov 函数设计了一个简单的自适应同步控制器，将两个初始值参数未知混沌系统行为同步，数值仿真证实了该方法的有效性与可实现性.

1 混沌系统的分析

根据Lorenz的混沌系统[1]，

(1)

在此基础上重新改写非线性项，则新的混沌系统如下:

(2)

其中x，y，z为系统变量，a，b，c，d为系统参数，当a=35，b=12，c=40，d=0．7，系统(2)存在一个混沌吸引子如图1所示，此时的Lyapunov指数稳态值分别为LE1=1．39、LE2=0．048、LE3=48．5，维数dL=2．03.

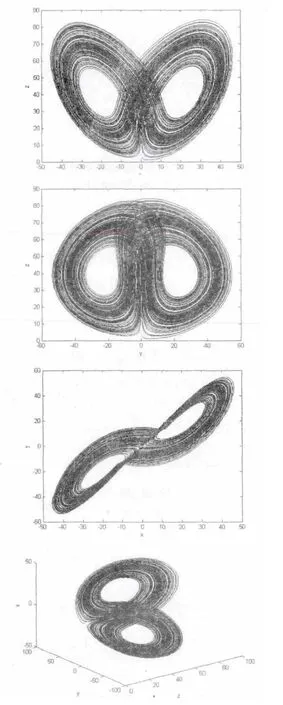
图1 三涡卷混沌吸收引子

1．1耗散性

新系统为耗散系统，由(2)式得：

这就意味着系统(2)具有耗散性，且以指数速率收敛，当t→∞时，包含系统轨线的每个体积元以指数速率收缩到0.因此，所有系统轨线最终会限制在一个体积为零的集合上，且渐近固定在一个吸引子上，即说明吸收引子存在性.

1．2平衡点及其稳定性

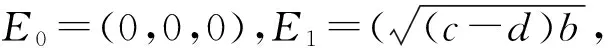
(3)

及多项式为

f(λ)=λ3+A2λ2+A1λ+A0.

(4)

令f(λ)=0， 将E0=(0，0，0) 代入 (4)， 选取参数a=35，b=12，c=40，d=0．7，求出λ1=23，λ2=-12，λ3=-59，其中λ1为正实根，λ2，λ3是负实根，根据Routh——Hurwitz判据，E0为不稳定鞍结点.

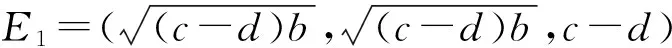
λ1=2．024 5+25．175 9i，

λ2=2．024 5-25．175 9i，

λ3=-51．748 9，

其中λ3为负实根，λ1，λ2是正实部的共轭复数.根据Routh——Hurwitz判据，E1为不稳定的焦结点，同样E2也为不稳定的焦结点.

由以上分析可知，三个平衡点都是不稳定的鞍或者焦结点，且是双涡卷混沌吸引子.

1．3 Lyapunov 指数及分岔图

参数的变化，从系统三个方向的Lyapunov指数和分岔图，可以直观看出系统运动状态的变化，下面就增加的两个参数下系统的Lyaunov指数与分岔图进行讨论研究.

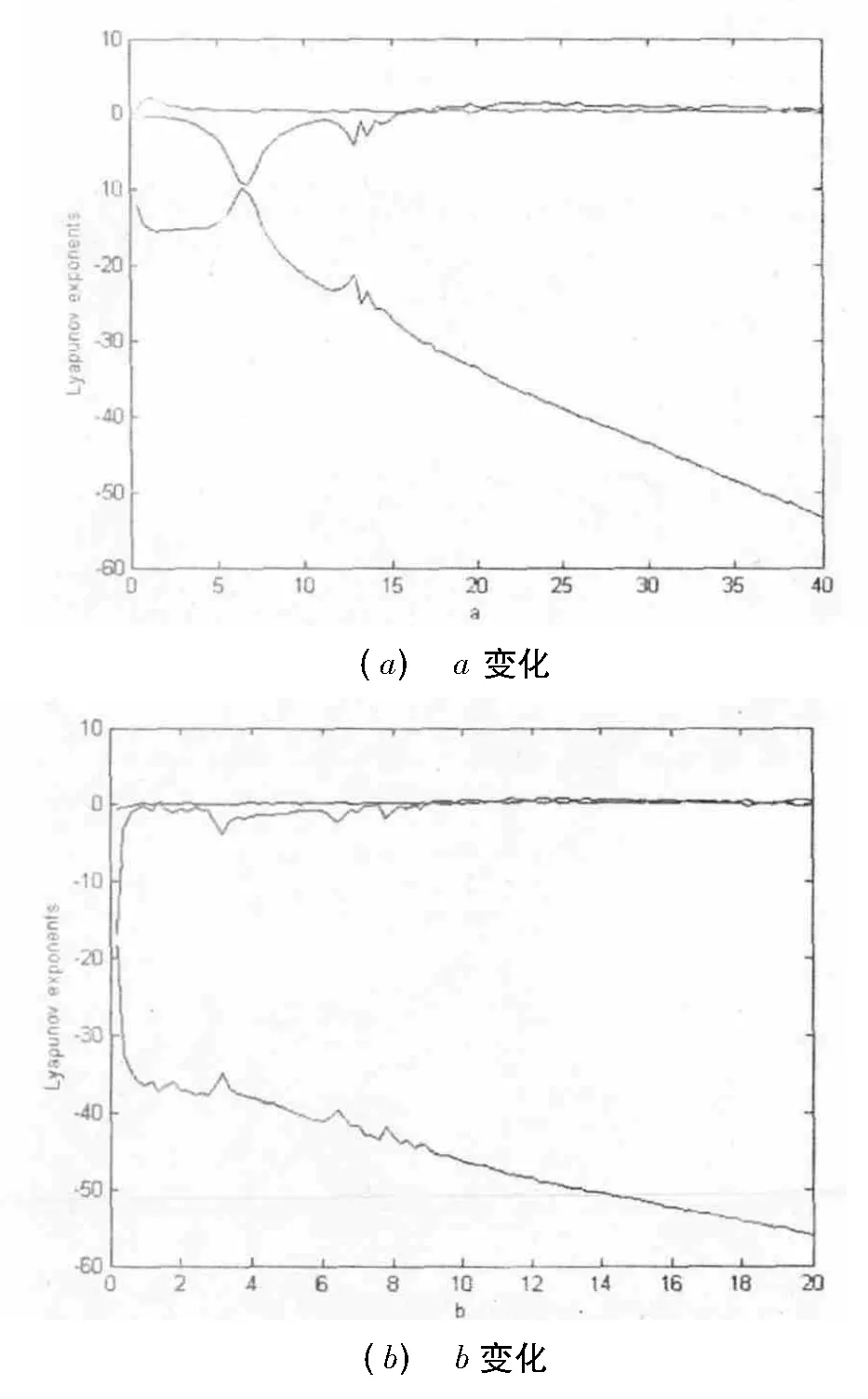
固定参数b=12，c=40，d=0．7，从图2(a)可以看出，当a∈[20，40]系统出现了一个正的Lyapunov指数，系统处于混沌状态.当a∈[0，20]，最大的Lyapunov指数为0，系统处于周期运动形式，如图2(a).同理可以分析其他参数.

固定参数a=35，c=40，d=0.7.从图2(a)可以看出，当a∈[10，40]U[1，2]系统出现了一个正的Lyapunov指数，系统处于混沌状态，如图2(b)与图3(a).对于参数c变化对系统影响如图2(c)所示，对于参数d对系统影响如图3(b)所示.

2 系统电路原理图及方程

对新的混沌系统(1)进行电路设计，根据系统(1)的状态表达式，设计电路图如图4.系统(2)是由线性电阻，电容，运算放大器LM741和模拟乘法器AD633来实现的.因为LM741与AD633允许工作电压的限制，故将输出电压线性缩小为原来的0．1倍.

图4 系统(2)的电路原理图

根据电路图 ，写出其相应的振荡电路方程为

运用Mutisim10对电路进行了仿真，将水平轴线进行了调整，显示在示波器上且为实时显示.从仿真波形看，波形轨迹不重合，因此电路实现了混沌现象.

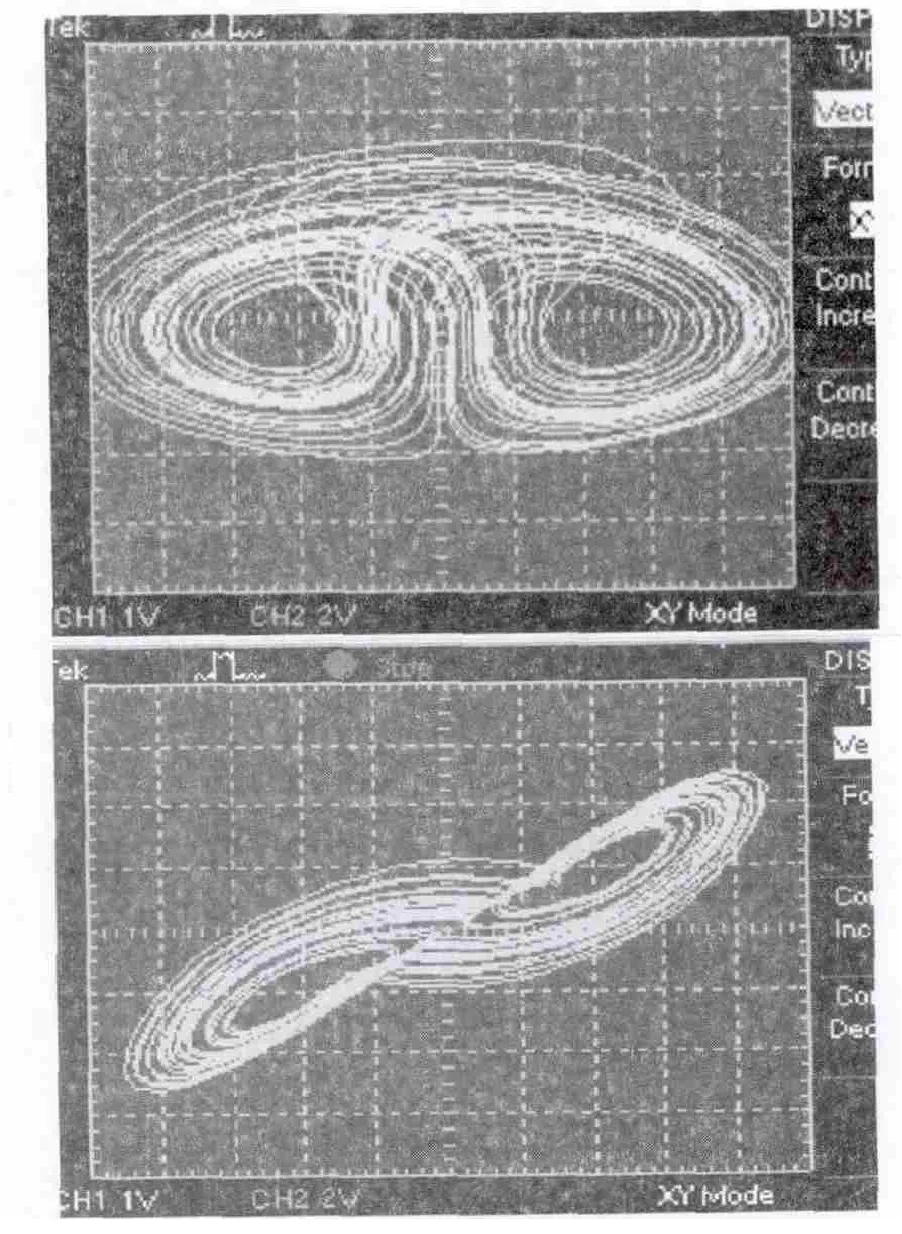
图5 系统(1)的仿真相图

混沌电路的搭建应该注意两个重要问题：1)对于电阻误差精度的选择，建议选择1%以下的电阻，对于非标的电阻可以通过串并实现.2)对于供电系统的选择，采用线性稳压电源，尽量避开开关电源的使用，因开关电源纹波较大，对于输出波形干扰较大.

上述的理论分析和数值仿真以及电路系统仿真均证明了新的一类混沌系统具有混沌系统共有的一切特征，因为其参数多和电路的可容易实现性，则该系统具有更多的潜在的应用价值如电路的抗干扰性，混沌通信和图像加密以及检测等.

3 自适应控制器的设计

为了更好地研究本系统，设计一种很简单的同步控制器，加以控制．

定义驱动系统为系统

(6)

响应系统为

(7)

式子(7)中u为控制输入，参数a，b，c，d是未知的.定义误差为定义误差

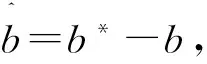
(8)

取Lyapunoy函数

(9)

函数V的导函数

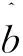
(10)

取控制率

(11)

自适应率

(12)

则

(13)

(14)

两边积分

(15)

同理可以证明ey，ez∈L2根据Barbalat引理，当t→∞，有ex，ey，ez→0，误差收敛零，则驱动系统(6)与响应系统(7)同步.

4 仿真结果

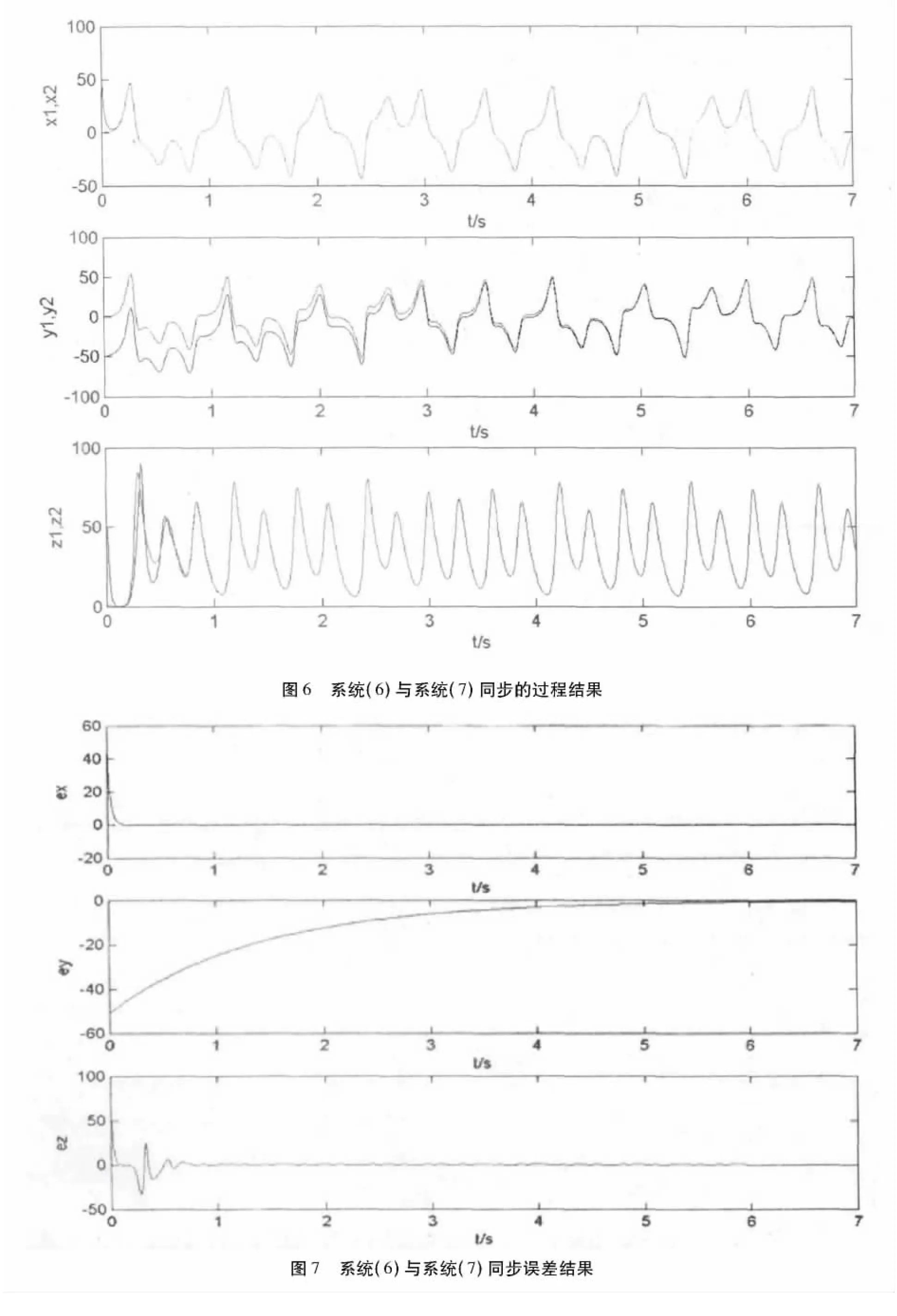
为了验证上述同步控制器的有效性，对该方法用matlab进行了仿真.取参数a=35，b=12，c=40，未知参数d=0．6，系统出现混沌现象.取两系统的初始条件分别是：x1(0)=-1，y1(0)=1，z1(0)=1，x2(0)=53，y2(0)=-56，z2(0)=56，d*(0)=1仿真的同步结果与误差结果如图6、图7.由图可见当t接近5 s左右时，驱动系统与响应系统三个状态量都达到了同步.

5 结论

本文对在Lorenz系统的基础上改进一类新的系统，进行数值仿真和电路仿真发现该系统的混沌吸引子形状有别于Lorenz 系统.通过计算了该系统的平衡点及其稳定性、数值仿真和电路仿真验证了该系统丰富的动力学特性.基于 Lyapunov稳定性原理，设计一种的自适应同步控制器，实现了新的混沌系统的同步．得出仿真结果， 从而证实了该方法的可行性及可实现性.本文研究的系统参数较多，并且可以用电子振荡器电路来实现，所以该系统可广泛应用于电图像加密等领域，当然也是作者下一步的研究方向．

[1] LORRNZ E N． Deterministic nonperiodic flow[J]．J Atmos．Science，1963，20(2):130-141．

[2] CHEN G,UETA T．Yet another chaotic attractor[J]．International Journal of Bifurcation and chaos，1999，9(7):1465-1466．

[3] Lü J H， CHEN G R． A new chaotic attractor coined[J]．International Journal of Bifurcation and chaos，2002，12(3): 659-661．

[4] LIU C X,LIU T，LIU L．A New Chaotic Attractor[J]．Chaos，Solitons and Fractals，2004，22(5):1031-1038.

[5] 王震，孙卫．T混沌系统的动力学分析与同步及电路仿真[J]．物理学报，2013， 62(2)：020511．

[6] 杜文举，俞建宁，安新磊，等．一个新的四翼混沌系统的动力学分析[J]． 云南民族大学学报:自然科学版 ，2013，22(4):275-279．

[7] 高智中．一个新的四维超混沌系统及其分析[J]．武汉大学学报:理学版，2011，57(3): 201-204．

[8] REN H P ，BAPTIST M ，GREBOGI C .Wireless communication with chaos[J]，Physics Review Letter，2013，110(18):184101.

[9] 任海鹏，刘丁.基于贝努力映射和CPLD的混沌A/D转换器[J]，仪器与仪表学报，2007，28(1):42-47．

[10] 雷腾飞，陈恒，王震，等．分数阶永磁同步风力发电机中混沌运动的自适应同步控制[J]．曲阜师范大学学报：自然科学版，2014，40(3)：63-68．

[11] 吴忠强，奥顿．线性连续系统混沌跟踪控制的T-S模型方法[J]．电机与控制学报， 2007， 11(2):201-206．