基于TI-DWT-MSSNF的谱光滑与评价

李 磊 庹先国 刘明哲 石 睿 王 俊

1（成都理工大学 地质灾害防治与地质环境保护国家重点实验室 成都 610059）

2（成都理工大学 地学核技术四川省重点实验室 成都 610059）

3（西南科技大学 核废物与环境安全国防重点学科实验室 绵阳 621010）

基于TI-DWT-MSSNF的谱光滑与评价

李 磊1,2庹先国1,3刘明哲1,2石 睿1,2王 俊1,2

1（成都理工大学 地质灾害防治与地质环境保护国家重点实验室 成都 610059）

2（成都理工大学 地学核技术四川省重点实验室 成都 610059）

3（西南科技大学 核废物与环境安全国防重点学科实验室 绵阳 621010）

提出了基于平移不变离散小波变换(Translation Invariant Discrete Wavelet Transform, TI-DWT)小波模极大值空间选择性滤波(Translation Invariant Discrete Wavelet Transform Wavelet Modulus Maxima Spatial Selectivity Filter, TI-DWT-MSSNF)的能谱平滑算法，并构建了光滑效果评价指标。分别使用α谱仪和γ谱仪获取了239Pu、241Am的α能谱和137Cs的γ能谱，将5点3次多项式最小二乘法、传统的小波模极大值法和TI-DWT-MSSNF分别用于α和γ谱平滑处理。结果表明：相比较5点3次多项式最小二乘法和传统的小波模极大值法，TI-DWT-MSSNF消除统计涨落更加彻底，特征信息保留更好，峰形畸变更小，是一种更优的方法。

平移不变离散小波变换，模极大值，光滑效果评价

核衰变和探测器计数的统计涨落及电子学系统噪声是固有存在的。在放射性测量时，实测谱的统计涨落也是固有存在的，通常表现为不光滑，固有的物理规律被统计涨落所掩盖。尤其在低水平放射性测量或者计数时间很短时，在峰区内道计数较少，计数最多的道不一定就是特征峰的期望值，甚至还有可能峰被淹没在统计涨落之中。为了可靠地识别特征峰的存在，并且准确地确定峰的位置及对应射线的能量，就有必要对实测谱进行光滑处理。传统的谱光滑方法[1]有：重心法、算术滑动平均法、多项式最小二乘法、离散函数褶积滑动变换法等，其基本思想是选取不同的平滑窗口逐点对实测谱进行处理，以待处理点为中心，用其左右m道的测量数据对该道的数据加以修正，从而不同程度地消除统计涨落的影响。实际运用时，可根据实际情况，选择相应方法进行数据处理。但它们在消除统计涨落的同时，往往也会造成能谱失真，如峰形畸变、丢失弱峰、衍生干扰峰等。

傅里叶变换(Fourier Transform, FT)法[2]改变了逐点处理的思想，而采取全局化处理，其基本思想是将时频域转换为与之对应的能频域，根据噪声谱的频率集中在高频段而信号谱的频率集中在低频段的基本特性，选取合适的滤波器，部分或全部除去高频的噪声谱，尽可能地保留信号谱，达到消除统计涨落的目的。

小波变换(Wavelet Transform, WT)是在FT的基础上发展起来的一种信号处理方法，具有良好的时频局部化特性和多分辨率分析能力，已被成功运用于多个领域[3-4]。近年来，离散小波变换(Discrete Wavelet Transform, DWT)在γ谱、X荧光谱、α谱等谱光滑方面有着较多的研究[5-7]。但是，DWT有一个明显的不足就是缺乏时移不变性。这意味着输入信号微小的变化就能导致不同尺度下DWT系数能量分布的大幅度变化。针对这一问题，Coifman等[8]提出了平移不变离散小波变换(Translation Invariant Discrete Wavelet Transform, TI-DWT)，已被用于信号和图像处理等多个领域[9-10]。

Mallat[11]和Meyer[12]都指出了小波模极大值与信号奇异性的关系，信号的小波模极大值随分解尺度的增加呈指数增加，噪声的小波模极大值随分解尺度的增加而减小。据此，Mallat等[11]提出了运用小波模极大值进行压缩去噪，并成功应用于图像处理。吴荔清[13]、袁华[14]等也各自提出了基于小波模极大值理论的消噪算法。Xu等[15]提出空间选择性滤波(Spatially selective noise filtration, SSNF)算法，将相邻尺度的小波系数进行相关比较，保留信号产生的模极大值及其邻域的小波系数，削弱噪声成分，减小了失真程度。然而，上述这些算法没有考虑小波模极大值会随分解尺度发生“漂移”这一事实，从而无法准确追踪模极大值[16]。TI-DWT的时移不变性已被证实能够解决模极大值随尺度“漂移”问题[8]。

本文提出一种基于TI-DWT的小波模极大值空间选择性滤波算法(Translation Invariant Discrete Wavelet Transform Wavelet Modulus Maxima Spatial Selectivity Filter, TI-DWT-MSSNF)。其基本过程是：首先对实测谱进行多尺度TI-DWT变换，其次从最大尺度开始，寻找每一尺度下小波系数极大值，利用模极大值理论分辨信号和噪声，然后进行空间选择性滤波处理，最后对处理后的数据进行重构，得到消噪后的谱线。本研究拟分别运用5点3次多项式最小二乘法、传统的小波模极大值法(Wavelet Transform Modulus Maxima, WTMM)和TI-DWT-MSSNF对实验测得的中高水平的γ谱和低水平的α谱进行光滑处理；对WTMM和TI-DWT-MSSNF的小波函数、分解尺度和小波阈值进行讨论；针对标准谱往往未知这一事实，构建一种新的光滑效果评价指标。

1 方法与原理

1.1 数据来源

1.1.1 α谱数据

实验使用ORTEC-8路α谱仪，239Pu和241Am的混合源（活度为13 Bq·2π-1），单次测量5min，取5次测量的平均值作为最终分析能谱数据。

1.1.2 γ谱数据

实验使用四川新先达公司提供的NaI(Tl)探测器（对137Cs源661keV的分辨率为7%），测量透过水介质后的射线，单次测量4min，取5次测量的平均值作为最终分析的能谱数据。

1.2 平移不变离散小波变换(TI-DWT)

TI-DWT是一种非正交小波变换，其基本思想是在每一尺度下引入反馈回路，移位补偿DWT过度扼杀的小波系数，从而克服模极大值的“漂移”现象，详见图1。这里x[n]表示离散的待处理数据，H1和H0是一对高、低通互补的小波滤波器，dj,k和aj,k分别是尺度j下第k个详细小波系数和近似小波系数。圆形箭头表示移位处理，其值为aj,kMod（N/2’）。设数据长度为N，分解尺度为J，TI-DWT变换后生成一包含所有可能平移量的NJ×矩阵。经移位补偿后构成新的小波系数，实现平移不变。

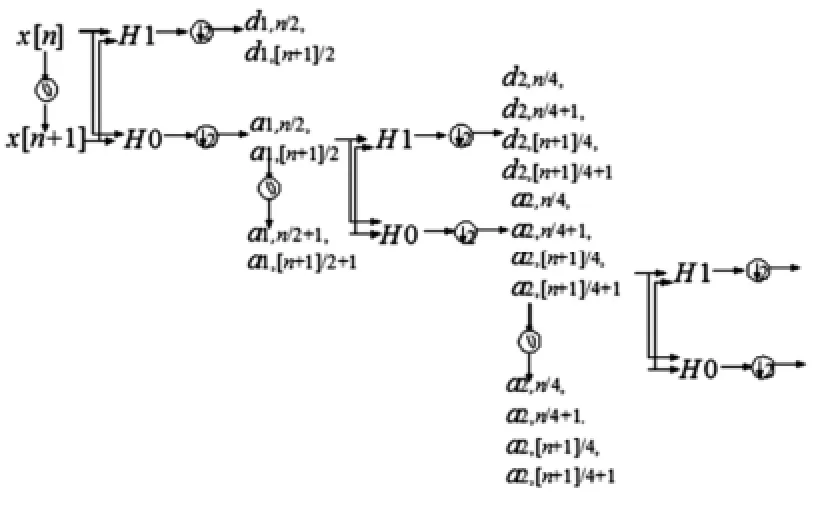
图1 三层TI-DWT分解滤波器组框图Fig.1 Filter bank for a 3-level TI-DWT decomposition.

1.3 小波变换的模极大值

对任意函数w(t)，引入记号ws(t)，若满足：

则ws(t)表示在尺度因子s下的伸缩。某一尺度a0下，若存在一点(a0, τ0)使得：

则称点(a0, τ0)是局部极值点，且在τ=τ0有一过零点。若τ0的某一领域内有任意一点，满足：

则称(a0, τ0)为小波变换的模极大值点。尺度空间(a, τ)中所有模极大值点的连线称为模极大值线。

1.4 信号的奇异性及Lipschitz α指数

信号的奇异点及不规则的突变点部分经常带有比较重要的信息。通常情况下，信号的奇异性有两种情况：一是信号在某个时刻内，幅值发生突变，引起信号的非连续。幅值的突变处是第一类间断点；二是信号外观上很光滑，幅值没有突变，但信号的一阶导不连续，称为第二类间断点。利用小波变换模极大值分析信号时，有用信号和噪声的小波系数有着明显差别。信号的局部奇异性通常用李普西兹(Lipschitz)指数α进行描述。Lipschitz α指数定义为：

则称s(t)为点t0的Lipschitz α指数。若所有且均满足式(4)，则称s( t)在(a, b)内是一致Lipschitz α。某一点的Lipschitz α表征了该点的奇异性大小。一般来说，α越大，该点的平滑度越高；α越小，该点的奇异性越大。

1.5 小波模极大值与Lipschitz α的关系

一般来说，随着分解尺度的增加，对Lipschitz α大于零的点（包括非奇异点，即1α≥的点），其小波变换系数的模极大值将呈幂增加趋势；而对于Lipschitz α小于零的奇异点，小波变换系数的模极大值将随着分解尺度的增加而减小。

因此，分解尺度、小波模极大值、Lipschitz α的关系可总结为：

(1) 常用信号的Lipschitz α大于零，其小波变换系数的模极大值随分解尺度而增大；

(2) 噪声服从处处奇异的随机分布，它具有负的Lipschitz α，其模极大值随尺度的增大而减小。

2 算法实现

如前所述，TI-DWT-MSSNF是TI-DWT、SSNF[15]和WTMM[17]结合体，其算法可归纳为：

(1) 选取合适的小波函数和分解尺度，对实测谱进行尺度M的TI-DWT小波变换。值得注意的是TI-DWT的小波函数分解尺度的选择仍没有最佳的准则。文献[17]选取了bior2.6小波。尺度选取要适当，若尺度太小，噪声的模极大值衰减不充分，提取有用信号比较困难。若尺度太大，则会造成信号失真。文献[10]给出的尺度确定由式(6)计算而来，对γ谱为3，对α谱为5。

式中，()E j为尺度j的系数总能量；(,)cD i j是尺度j下的第i个详细小波系数；N为信号长度。最佳尺度为小波系数最高能量对应的尺度。

(2) 对每层小波系数进行阈值修正。选取一个阈值，小于该阈值的小波系数作为噪声滤除，得到新的小波系数。综合比较硬阈值函数、软阈值函数和文献[18]提出的新阈值函数的效果后，采用文献[18]的阈值函数进行模极大值修正本。函数如下：

式中，thr为阈值，thr=max(xj)；k为经验系数，0≤k≤1，当k=0时，相当于硬阈值，当k=1时，相当于软阈值，取k=0.5；jtx和jtη分别为修正前后第j层第t个小波系数；sign为符号函数。

(3) 在新的小波系数基础上，寻找每个尺度上的局部极值点。若小波系数(,)W b a满足：

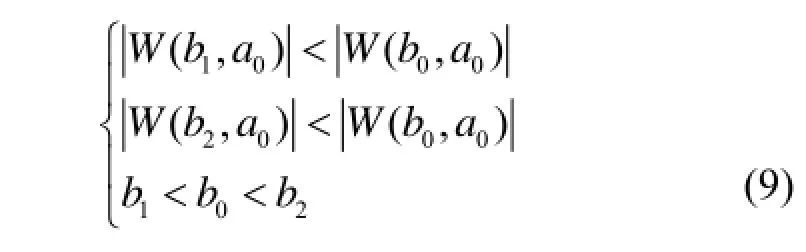
(4) 寻求模极大值点。

(5) 空间选择性滤波处理。对每个尺度上的小波系数进行空间相关运算：

式中，取l=2。然后，将Corrl(m, n)进行比例变换，使其与该尺度的小波系数能量相等，即：

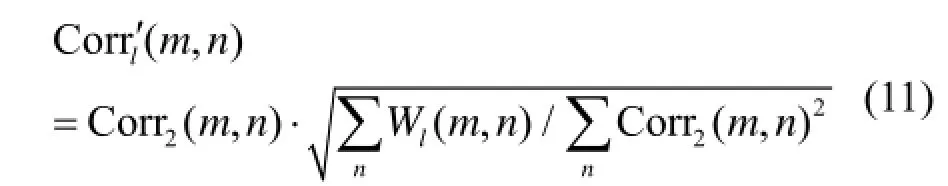
(6) 重复步骤(3)-(5)，直到所有尺度处理完毕。

(7) 对处理完的小波系数进行重构，即得消噪后的信号。

3 结果与评价

同一种光滑方法对不同信噪比的谱的光滑效果有所不同。因此，分别运用5点3次多项式最小二乘法、WTMM和TI-DWT-MSSNF对实验测得的中高水平、信噪比较小的γ谱和低水平、信噪比较大的α谱进行了光滑处理。为对光滑效果进行评价，采取视觉效果和数值判断两种方法评价光滑效果。

3.1 视觉效果及分析

图2(a)-(d)分别为实测：γ原始能谱、5点3次光滑谱（简化为5-3）、WTMM光滑谱、TI-DWT-MSSNF光滑谱。图3(a)-(d)分别为实测：低水平的α谱、5点3次光滑谱、WTMM光滑谱、TI-DWT-MSSNF光滑谱。

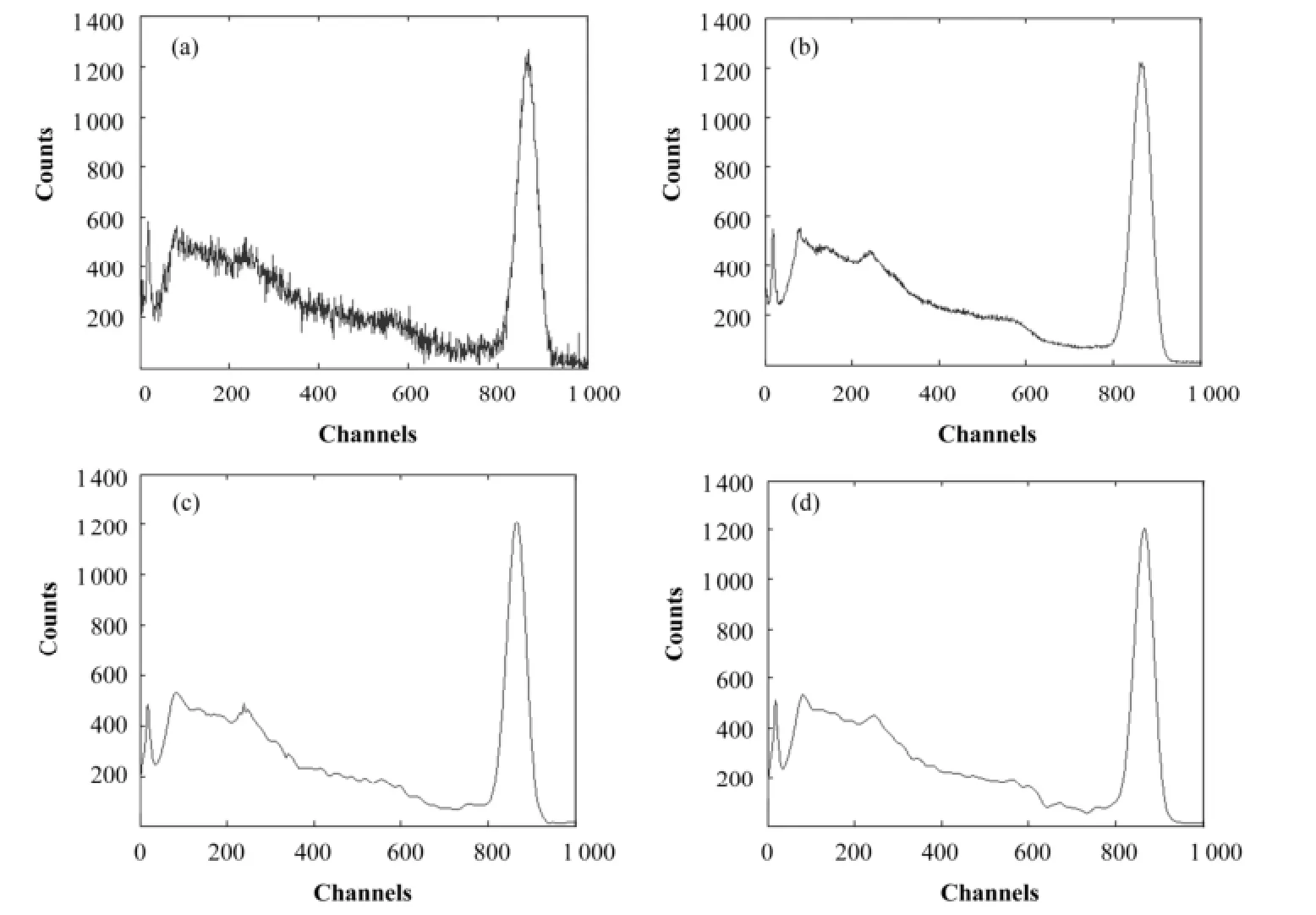
图2 γ谱5点3次、WTMM和TI-DWT-MSSNF光滑效果对比图(a) 实测的γ谱，(b) 5点3次光滑后的γ谱，(c) WTMM光滑后的γ谱，(d) TI-DWT-MSSNF光滑后的γ谱Fig.2 Results of γ spectrum using cubical smoothing algorithm with five-point approximation (5-3), WTMM, TI-DWT-MSSNF. (a) Measuring γ spectrum, (b) 5-3, (c) WTMM, (d) TI-DWT-MSSNF

图3 α谱5点3次、WTMM和TI-DWT-MSSNF光滑效果对比图(a) 实测的α谱，(b) 5点3次光滑后的α谱，(c) WTMM光滑后的α谱，(d) TI-DWT-MSSNF光滑后的α谱Fig.3 Results of α spectrum using cubical smoothing algorithm with five-point approximation (5-3), WTMM, TI-DWT-MSSNF. (a) Measuring α spectrum, (b) 5-3, (c) WTMM, (d) TI-DWT-MSSNF

由图2可知：在γ特征峰位高能端，5点3次、WTMM和TI-DWT-MSSNF光滑效果相当，因为高能端噪声较小；在低能端，WTMM和TI-DWTMSSNF光滑效果相当，均优于5点3次光滑，5点3次光滑后的γ谱有轻微的统计涨落。因为低能端噪声严重，5点3次光滑的能力有限，只有增加次数可以使光滑效果有所改善，但同时也压低了谱峰，这也说明WTMM和TI-DWT-MSSNF对高噪声有较好的抑制作用；在特征峰识别方面，三种方法都能识别γ谱的特征峰，该谱线的特征峰是单峰且计数高，所以这条谱线无法证明三者的特征峰识别能力。

由图3可知：在高能端，因为噪声相对较小，5点3次光滑、WTMM和TI-DWT-MSSNF的光滑效果相当；在低能端，因为噪声非常严重，5点3次光滑后的α谱噪声仍比较严重，其原因和图2分析一致，WTMM和TI-DWT-MSSNF的光滑效果相当，都有轻微的噪声；在特征峰识别方面，从局部放大图，5点3次光滑仅只是降低了信噪比水平，看不见239Pu的5.1429MeV特征峰和241Am的5.443MeV的特征峰，WTMM能看见239Pu的5.1429MeV特征峰，但仍具有一定的噪声，TI-DWT-MSSNF能清晰地看见239Pu的5.1429MeV特征峰，但对于241Am 5.443MeV的峰，WTMM和TI-DWT-MSSNF都存在假峰干扰。

3.2 数值方法

能谱光滑的基本原则是尽可能完整地保留特征信息，同时又尽可能多地去除噪声。因此，外观上的评价是很片面，必须对光滑谱进行定量的评价。常用的数值评价指标有信噪比(Signal to Noise Ratio, SNR)、峰信噪比(Peak Signal to Noise Ratio, PSNR)、均方根误差(Mean Squared Error, MSE)等[16,19]，但这些指标都只反映了光滑程度，而事实上，过度光滑会造成能谱畸变。因此，建立了新的评价指标：标准差(D(r))和卡方值(χ2)。

根据文献[20]，设实测的数据与光滑后的数据之间的偏差为r：

式中，ir为实测数据与光滑后的数据的每个对应点之间的加权偏差；if是第i道光滑后的数据；iy是第i道实测的数据。由贝塞尔公式[21]得到加权偏差的标准差D(r)为：

显然，D(r)表征了消噪程度。D(r)=0，表示光滑无效果；D(r)越大，表示剔除的噪声越多，光滑效果越好。但光滑过度会导致信号失真，峰形畸变，因此有必要建立另一个能反映能谱畸变情况的指标。

χ2在数理统计中用于非线性回归分析拟合效果评价[22]，是反映畸变的一个重要指标，其值越接近1，畸变越小。

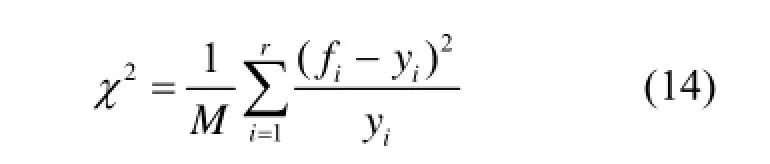
式中，M为自由度，M=r-l；l和r分别为被光滑谱段的左右道址。

综上可知，D(r)越大，χ2越接近于1，则光滑效果越好。分别计算了对γ谱、α谱进行5点3次光滑、WTMM光滑和TI-DWT-MSSNF光滑谱的D(r)值和χ2，详见表1。由表1可知，三种方法对峰高(H)都有不同程度的压缩，对信噪比较高的γ谱，TI-DWT-MSSNF光滑后的峰高略大于5点3次光滑和WTMM光滑后的峰高，对于信噪比较低、低水平的α谱，5点3次光滑法在数值上没有比较的意义，TI-DWT-MSSNF两峰高值都要大于WTMM，表明TI-DWT-MSSNF优于WTMM。

表1 γ谱和α谱5点3次光滑、WTMM光滑和TI-DWT-MSSNF光滑结果对比Table 1 Smoothing results of γ and α spectra using cubical smoothing algorithm with five-point approximation (5-3), WTMM, TI-DWT-MSSNF.

4 结语

谱光滑的主要目的是降低放射性测量中能谱的统计涨落，为后续更精确地解谱分析作预处理。根据小波模极大值理论，结合TI-DWT和SSNF的优点，提出了基于TI-DWT的小波模极大值空间选择性滤波算法，并分别运用于中高水平的γ谱和低水平的α谱消噪中，选用了新的数值评价指标，分别从效果图和数值方法对光滑结果进行了评价。综合研究表明，相比较5点3次多项式最小二乘法和传统的小波模极大值法，TI-DWT-MSSNF消除统计涨落更加彻底，能更好地保留特征信息，峰形畸变更小，是一种更优的方法。

1 庞巨丰. γ能谱分析[M]. 陕西: 陕西科学技术出版社, 1990: 542-566 PANG Jufeng. Gamma spectra data analysis[M]. Shanxi: Shanxi Science and Technology Press, 1990: 542-566

2 Rao K R, Kim D N, Hwang J J. Fast Fourier transform: algorithms and applications[M]. New York: Spring-Verlag, 2008: 4-70

3 Arivazhagan S, Ganesan L. Texture classification using wavelet transform[J]. Pattern Recognition Letters, 2003, 24(9-10): 1513-1521

4 Du P, Kibbe W A, Lin S M. Improved peak detection in mass spectrum by incorporating continuous wavelet transform based pattern matching[J]. Bioinformatics, 2006, 22(17): 2059-2065

5 Xiao G, Deng L, Zhang B N, et al. A nonlinear wavelet method for data smoothing of low-level gamma-ray spectra[J]. Journal of Nuclear Science and Technology, 2004, 41(1): 73-76

6 Bury P, Ennode N, Petit J M, et al. Wavelet analysis of X-ray spectroscopic data, Part 1, the method[J]. Nuclear Instruments and Methods in Physics Research Section A, 1996, 383(2): 572-588

7 石睿, 庹先国, 张金钊, 等. 基于离散小波变换的低水平α能谱光滑与评价[J]. 核技术, 2013, 36(12): 120201 SHI Rui, TUO Xianguo, ZHANG Jinzhao, et al. Smoothing and evaluation of low level alpha spectra based on DWT method[J]. Nuclear Techniques, 2013, 36(12): 120201

8 Coifman R R, Donoho D L. Translation-invariant de-noising[M]. Wavelets and Statistics Lecture Notes in Statistics, 1995, 103: 125-150

9 Berkner K, Wells R O. Smoothness estimates for soft-threshold de-noising via translation-invariant transform[J]. Applied and Computational Harmonic Analysis, 2002, 12(1): 1-24

10 Oliveira M H, Rocha L C D, Salles T C M, et al. Partial discharge signal de-noising with spatially adaptive wavelet thresholding and support vector machines[J]. Electric Power Systems Research, 2011, 81: 644-659

11 Mallat S, Zhong S. Characterization of signals from multi-scale edges[J]. IEEE Transactions Pattern Analysis Machine Intelligence, 1992, 14(7): 710-732

12 Meyer Y. Wavelets and applications[C]. Proceedings of the International Congress of Mathematicians, Kyoto, Japan, 1990: 1619-1626

13 吴荔清, 李波, 刘润华. 小波去噪和奇异性分析方法在输油管道泄漏检测中的应用[J]. 科学技术与工程, 2008, 8(9): 2450-2454 WU Liqing, LI Bo, LIU Runhua. Application of the de-noising and singularity analysis based on wavelet transform in the oil pipeline leakage detection[J]. Science Technology and Engineering, 2008, 8(9): 2450-2454

14 袁华, 张卫宁, 路俊, 等. 一种改进的小波去噪中模极大值处理的方法[J]. 系统仿真学报, 2005, 17(4): 838-843 YUAN Hua, ZHANG Weining, LU Jun, et al. An improved method of wavelet de-noising from its wavelet transform modulus maxima[J]. Journal of Sustem Simulation, 2005, 17(4): 838-843

15 Xu Y S, Weaver J B, Dennis M, et al. Wavelet transform domain filter: a spatially selective noise filtration technique[J]. IEEE Transactions on Image Processing, 1994, 3(6): 747-758

16 陶维亮, 王先培, 刘艳, 等. 基于小波模极大值移位相关的光谱去噪方法[J]. 光谱学与光谱分析, 2009, 29(5): 1241-1245 TAO Weiliang, WANG Xianpei, LIU Yan, et al. A denoising algorithm for absorption spectra by wavelet transform modulus maxima shift-related filter[J]. Spectroscopy and Spectral Analysis, 2009, 29(5): 1241-1245

17 于国梁. 用小波分析方法检测γ谱弱峰的可行性研究[D].四川大学, 2005: 35-38 YU Guoliang. The study of feasibility to detect low signal in gamma-ray spectra using wavelet analysis[D]. Sichuan University, 2005: 35-38

18 张新军, 刘鸿福, 张和生. 应用小波新阈值函数对地方蛇形活性炭测氡γ能谱的消噪[J]. 原子能科学技术, 2010, 44(8): 897-901 ZHANG Xinjun, LIU Hongfu, ZHANG Hesheng. Denoising low activity γ-ray spectra of radon absorbed in activated charcoal by using wavelet thresholding function[J]. Atomic Energy Science and Technology, 2010, 44(8): 897-901

19 万智萍. 一种高效的小波contourlet变换阈值去噪算法[J]. 激光与红外, 2013, 43(7): 831-836 WAN Zhiping. Efficient image denoising method based on wavelet-contourlet transform and threshold[J]. Laser and Infrared, 2013, 43(7): 831-836

20 雷卫国, 王铁山, 冯天成, 等. 一种γ能谱光滑效果评价方法[J]. 核电子学与探测技术, 2012, 32(3): 308-310 LEI Weiguo, WANG Tieshan, FENG Tiancheng, et al. A smoothing effect evaluation method of γ spectrum[J]. Nuclear Electronics and Detection Technology, 2012, 32(3): 308-310

21 费业泰. 误差理论与数据处理[M]. 北京: 机械工业出版社, 2004: 15-17 FEI Yetai. Error theory and data processing[M]. Beijing: Mechanical Industry Press, 2004: 15-17

22 Li Z, Tuo X G, Yang J B, et al. Statistical distribution based detector response function of a Si (PIN) detector for Kαand KβX-ray[J]. Chinese Physics C, 2013, 37(1): 018202

CLCTL9

Smoothing and evaluation of spectrum based on TI-DWT-MSSNF

LI Lei1,2TUO Xianguo1,3LIU Mingzhe1,2SHI Rui1,2WANG Jun1,2
1(State Key Laboratory of Geohazard Prevention & Geoenvironment Protection, Chengdu University of Technology, Chengdu 610059, China)2(Provincial Key Laboratory of Applied Nuclear Techniques in Geosciences, Chengdu University of Technology, Chengdu 610059, China)3(Laboratory of National Defense for Radioactive Waste and Environmental Security, Southwest University of Science and Technology, Mianyang 621010, China)

Background: Nuclear decay, electronic noise, statistic fluctuations, etc., exist inherently. Therefore, the measured spectrum always has statistic fluctuation. Purpose: In order to reduce the statistical fluctuation and electronics noise in detector, translation invariant discrete wavelet transform (TI-DWT) wavelet modulus maxima spatial selectivity filter (TI-DWT-MSSNF) smoothing algorithm was put forward to preprocess data for the de-convolution of spectrum. Methods: The α-spectrum was acquired by using ORTEC-8 channel α spectrometer to measure the source numbered AMPU1103 (239Pu and241Am) under vacuum conditions of -0.03MPa. The γ-spectrum was obtained by using γ spectrometer and137Cs source. Cubical smoothing algorithm with five-point approximation (“5-3”), the traditional method of wavelet modulus maxima (WTMM) and TI-DWT-MSSNF were applied to smooth α and γ spectra. Results: The study showed that TI-DWT-MSSNF method could eliminate statistical fluctuation more thoroughly, retain feature information better compared with “5-3” and WTMM. The D(r)values of TI-DWT-MSSNF were greater and χ2values of TI-DWT-MSSNF were more close to 1 compared with those of “5-3” and WTMM. Conclusion: Comprehensive research indicates that it is feasible to reduce the statistical fluctuations of spectrum using TI-DWT-MSSNF. And TI-DWT-MSSNF outperforms both the “5-3” and WTMM.

Translation invariant discrete wavelet transform (TI-DWT), Modulus maxima, Smoothing evaluation

TL9

10.11889/j.0253-3219.2014.hjs.37.120203

国家杰出青年科学基金项目(No.41025015)、国家自然科学基金项目(No.41274130)、四川省青年科技创新研究团队项目(No.2011JTD0013)、四川省科技支撑计划(No.2013FZ0022)资助

李磊，男，1989年出生，2012年毕业于成都理工大学，现为硕士研究生，核能与核技术工程

庹先国，E-mail: 13982021384@163.com

2014-01-26，

2014-09-05