一种基于条件信度参数证据网络的态势感知方法

郭 强，关 欣，周 勋，张 杨，孙贵东

(1.海军航空工程学院 信息融合研究所,山东烟台 264001；2.海军航空工程学院 电子信息工程系,山东烟台 264001；3.海军装备部,西安 710054；4.海军航空工程学院 训练部,山东烟台 264001)

0 引 言

态势感知将处于复杂战场环境下的多平台多传感器所观测到的所有目标的不确定异类状态信息，通过与情报信息、环境因素及专家先验知识等条件有机地联系起来，获得战场兵力、电子战武器部署情况、军事活动意图及敌我双方平台的分布、航向和速度等变化趋势的统一的态势信息，来支持上层做出快速正确的战场决策。态势感知和估计处于JDL信息融合模型中的第二级，位于位置估计、目标识别之上，不仅需要综合多平台异类传感器不确定信息，而且还需要基于客观条件和先验知识进行有效的不确定性知识推理，得到更抽象、更直观、更有利于决策的隐含知识。态势感知的核心就是多源异类传感器信息融合，以及不确定性知识的推理问题。

为了解决多源异类知识框架下的不确定性信息融合、推理问题，基于网络模型的知识表示和不确定推理方法得到了广泛的研究[1,2]。贝叶斯网络(BN)[3]作为贝叶斯理论与图论相结合的不确定性知识处理方法，将不确定性先验知识以先验概率和条件概率的形式进行表示并形成有向无环图的网络知识结构，对证据信息进行不确定性推理，该方法在故障诊断、专家系统、评估预测和军事系统等领域都得到了广泛的应用[4～10]。但是贝叶斯网络只能处理符合贝叶斯信度的精确证据，且无法区分不知道和不确定的知识，对不确定性推理带来了一定的局限。价值网络(VN)[11]作为一种综合多种不确定知识表示方法的理论框架，提出了将证据理论与图论相结合处理不确定性知识的方法。该方法通过边缘化和组合两种手段，对不同知识框架下的信息进行转换和融合，取得了很好的效果[12]。但是该方法的价值评价以不同框架的笛卡尔乘积的联合信度函数为基础，对于复杂的网络模型，需要很大的存储空间和运算量，推理效率较低。Xu Hong 和 Smets[13]最早提出了证据网络的概念，首次将知识网络结构中变量之间的关系用条件信度函数取代联合信度函数进行表示，相比价值网络推理，简化了不确定性推理的复杂度。

基于对条件信度参数的证据网络推理方法的研究，提出了一种基于条件信度参数证据网络的态势感知方法，首次将基于条件信度参数的证据网络应用于态势感知领域中，通过对比已有的基于联合信度参数证据网络的态势感知方法[14]，证明了本方法的优越性。

1 理论基础

1.1 乘积空间下的信度理论

对乘积空间的信度理论研究，需要定义两个基本的运算：扩展和边际化。

定义1 设X定义在识别框架ΘX上，Y定义在识别框架ΘY上，那么从ΘX到ΘX×ΘY的空扩展是一个定义在ΘX×ΘY上信度函数，其基本信度分配为

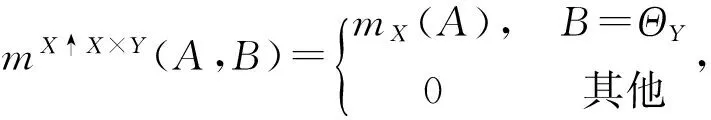
(1)

定义2 设X定义在识别框架ΘX上，Y定义在识别框架ΘY上，belX(x|y)是在给定y⊆ΘY时，ΘX上的条件信度函数，那么belX(x|y)在ΘX×ΘY上B扩展的得到的信度函数belX×Y定义为

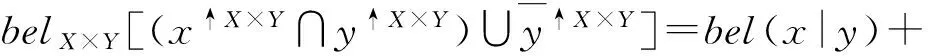
mX(φ|y)

(2)

B扩展得到的基本信度分配函数定义为

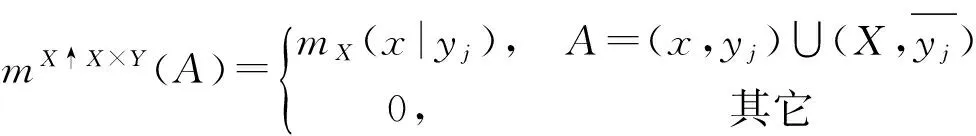
(3)

定义3 设X定义在识别框架ΘX上，Y定义在识别框架ΘY上，X的证据mX和Y的证据mY的合取定义在ΘX×ΘY上，

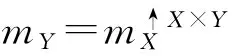
(4)

定义4 设m是X上的基本信度分配，Y⊆X,Y≠φ，m对Y的边际化表示为m↓Y

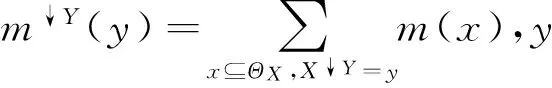
(5)

定理1 从联合信度函数表示的信息中，如求得条件信度函数，其中用到上述扩展和边际化等运算。设mXY是定义在识别框架ΘX×ΘY上的基本信度分配，那么条件基本信度分配mY(y|x):x⊆ΘX可以通过式(6)得到，

(6)

1.2 基于条件信度参数的证据网络理论

证据网络是一种有向无环图模型，由代表变量的结点和连接这些结点的有向边，以及相应的关系参数构成，是图论与证据理论的结合。形式化表示为EN={(N,A)，B}，N为结点的集合，A为结点间有向连接弧的集合，(N,A)即为一个具有N个结点的有向无环图G；B为结点之间的信度函数关系集合，其编码了一组变量之间的相互关系。基于条件信度函数的证据网络模型，就是网络参数即结点之间的关系B以条件信度函数表示的证据网络模型，如图1所示。结点集中的每个结点代表一个变量，变量一般是研究问题的抽象。有向边表示结点之间的因果关系或影响关系，箭头代表因果关系影响的方向性(由父结点指向子结点)，结点若无连接表示结点所对应的变量之间是无关的。

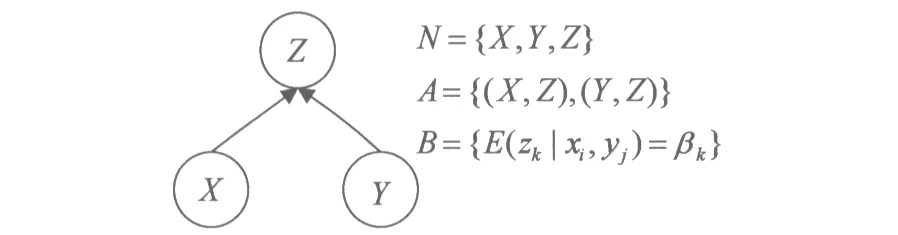
图1 基于条件信度参数的证据网络模型

1.3 基于条件信度参数的证据网络推理方法

基于条件信度函数的证据网络精确推理方法，实质上就是通过扩展和边缘化、条件信度转换，以及信度合成公式，在给定的证据网络结构和已知的证据下，计算网络结构中任意其他结点事件发生的信度。证据网络结构蕴含的独立性关系使得推理算法具有可操作性，独立性好的证据网络可以指数级的提高推理算法的效率。

1.3.1 条件信度参数的证据网络推理工具

Smets[15]提出的GBT理论(the generalized Bayesian theorem)和DRC准则(the disjunctive rule of combination)是证据网络推理的重要理论工具。

GBT理论作为贝叶斯理论的一般化方法，将所有的条件概率转化为信度函数。

定理1 对于任意xi∈ΘX和yi∈ΘY，基于GBT理论，条件信度函数belX(x)|y为

belX(x)|y=bX(x)|y-bX(φ)|y

(7)

(8)

由定义在乘积空间XY下的条件信度函数在y⊆ΘY条件下得到的信度函数，即在X上的边缘化结果，就是Smets提出的DRC准则。

定理2 对于任意xi∈ΘX和yi∈ΘY，基于DRC准则，条件信度函数belY(y)|x为

belY(y)|x=bY(y)|x-bY(φ)|x

(9)

(10)

对于网络中的每一个结点，边缘信度的更新需要计算相邻所有结点的传来的信息和自己的先验信息融合。假设结点Y向结点X传递信息，即证据网络推理的反向推理问题，结点X更新信度为

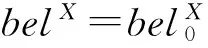
(11)

式中，belY→X代表子结点Y传来的信息，即

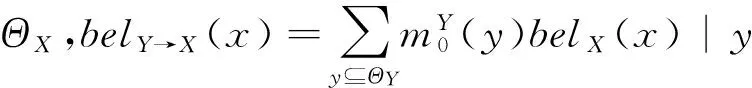
(12)

其中belX(x)|y是由GBT理论式(7)，(8)计算得到的。

同理，如果结点X向结点Y传递信息，即证据网络推理的正向推理问题，结点Y更新信度为

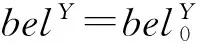
(13)

式中，belX→Y代表父结点X传来的信息，即

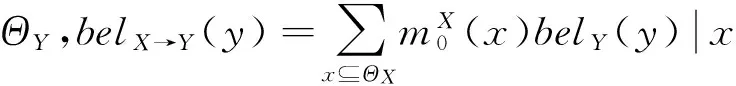
(14)

其中belY(y)|x是由DRC准则式(9)，(10)计算得到的。

2.2.2 基于条件参数证据网络的推理方法流程

设U为证据网络模型中一个有限个结点的集合，对于每一个结点X∈U，其父结点用Pa(X)表示，子结点用Ch(X)表示。在每一个结点X存储一个先验信度Bel0，同时存储它与父节点之间的条件信度函数{BelXY:Y∈Pa(X)}，当有一个结点得到一个观测证据时，该结点的信度就会被更新，并向其父结点传递消息(用λ值表示)，向其子结点传递消息(用π值表示)。证据网络图结构如图2所示。

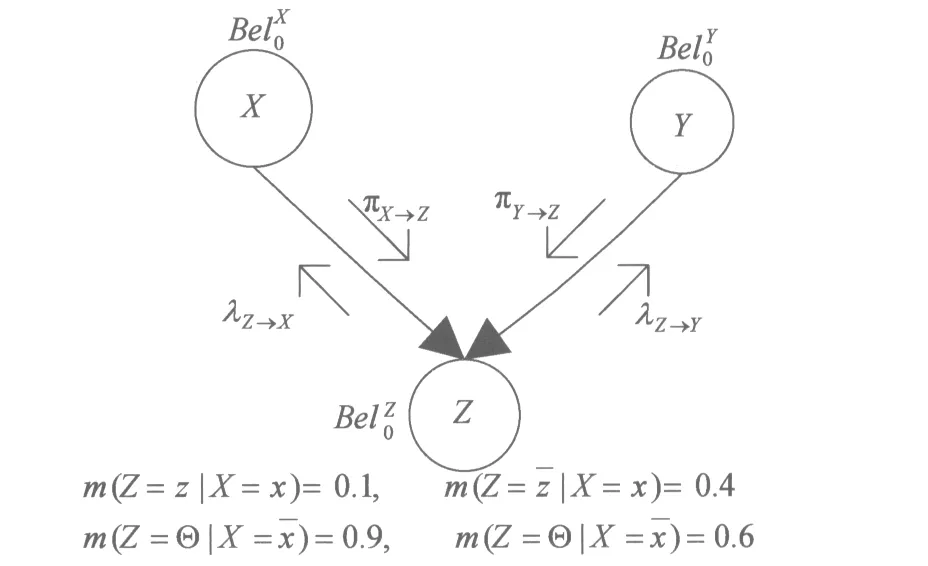
图2 证据网络图结构

基于条件参数证据网络的精确推理方法，应用基于PolyTree的消息传递算法。该方法的主要思想是在网络结点间进行消息传递：结点发送消息给其父结点和子结点，并接收其父结点和子结点传来的消息，每个结点具有一个λ值和一个π值，λ值由其子结点传递过来的消息计算得到，π值由其父结点传递过来的消息计算得到。结点的更新信度根据λ和π值求得。更新后再向自己相邻的结点传递λ和π值，直到证据网络所有的结点都得到了更新为止。这种算法基于每个结点上局部出现的信息进行计算，也成为局部算法。该方法的步骤如下。

a)信度初始化

(1)对于每一个结点X：

πX=belX

λX=空信度(Θx=1)

(2)对于每一个根结点X：

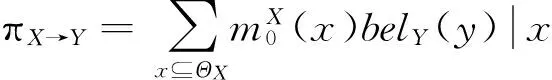
(3)当结点Y接收完所有父节点的信息后，得到

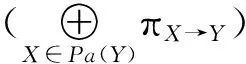
(15)

belY=πY⊕λY

(16)

同理，计算Y向所有子结点传播的信息。

b)更新过程

当在某个结点上有观测数据产生时，更新算法就要被激活，在该结点上计算所有传来的信息，然后计算该结点的λ值、π值及新的信度值和传出给相邻结点的信息。

(1)计算结点的观测信息、先验信息及相邻结点传来的信息融合后的更新的信度值

belX=πX⊕λX，

(17)

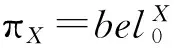
(2)计算结点传给相邻结点的信息

πX→Y代表父结点X向子结点Y传递的信息

(18)

λY→X代表子节点Y向父结点X传递的信息

(19)

c)更新算法直到网络中的每个结点都进行了更新后才停止。

3 基于条件信度参数证据网络的态势感知模型

基于专家先验知识综合空中战场环境，对空中目标态势感知首先进行基于网络结构的建模，如图3所示。图中，敌机平台与敌我特征存在因果关系，攻击意图与敌我平台、火控雷达状态、飞行姿态有关，攻击能力与攻击范围、攻击准备有关，态势威胁等级与攻击意图、攻击能力有关。基于态势感知的网络结构，分别构建基于条件信度参数和联合信度参数的网络结构如图4所示，比较图3和图4，网络结点的信息是一致的，不同的是结点之间的关系参数分为条件信度和联合信度两种方式，并且基于条件信度参数的证据网络模型的条件信度参数处，不需要将不同框架下的信息进行更高维度的转换，用矩形框代表；而基于联合信度参数的证据网络模型的联合信度参数处，需要将连接的因果联系的不同框架下的信息扩展到更高维度的空间，然后再利用证据理论在该空间进行融合，再通过边缘化到需要推理的变量空间上，因为结点处需要进行运算，用椭圆表示。

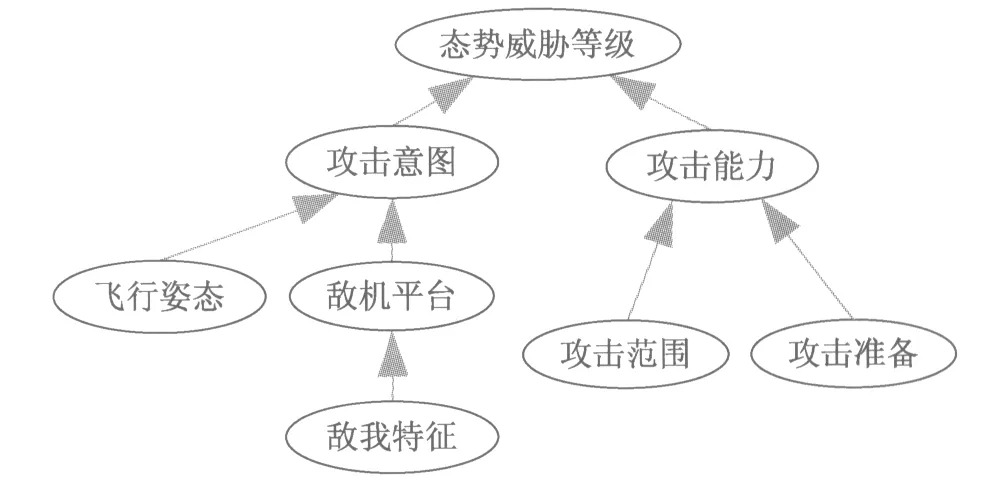
图3 空中目标态势感知网络结构模型

两种证据网络推理结构关系结点的参数表，见表1和表2，表中结点对应图4中的标注的四个结点。条件信度参数和联合信度参数可以通过扩展和边缘化进行相互转化，这里不再赘述，读者可以参照表1和表2。从表中可知，表示相同的先验知识，条件信度参数需要的存储量要远小于联合信度参数的存储量，联合信度参数随着焦元数量和取值范围的增多成指数倍增大。为了表述方便，这里定义态势威胁等级为TL，其框架为{H,M,L}，攻击意图为HI，其框架为{H,L}，攻击能力为C，其框架为{G,B}，飞行姿态为M，其框架为{T,F}，敌机平台为NF，其框架为{T,F}，敌我特征为IFF，其框架为{Y,N}，攻击范围为WE，其框架为{L,S}，攻击准备为I，其框架为{H,L}。

表1 条件信度参数表

表2 联合信度参数表

3 实例对比分析

假设某一时刻，战场态势感知系统接收到的第一级信息融合系统传来的信息为m(M=Y)=1,m(M=N)=0,m(IFF=Y)=1,m(IFF=N)=0,m(WE=L)=1,m(WE=S)=0,m(I=H)=1,m(I=L)=0.

3.1 基于条件信度参数的证据网络推理

(1)首先处理IFF结点传来的信息m(IFF=Y)=1,m(IFF=N)=0,经过结点4，运用正向推理方法得到NF结点的信息，

Bel(NF=T)=m(IFF=Y)·m(NF=T|IFF=Y)=0.05,

Bel(NF=F)=m(IFF=Y)·m(NF=F|IFF=Y)=0.95.

(2)NF结点与M结点的信息经过扩展后，经过结点2进行正向推理得到结点HI的信息，

Bel(HI=H)=m(M=Y,NF=T)·m(HI=H|M=Y,NF=T)+m(M=Y,NF=F)·m(HI=H|M=Y,NF=F)=0.05·0.7+0.95·0.3=0.32,

Bel(HI=L)=m(M=Y,NF=T)·m(HI=L|M=Y,NF=T)+m(M=Y,NF=F)·m(HI=L|M=Y,NF=F)=0.05·0.3+0.95·0.7=0.68.

(3)WE结点和I结点经过扩展后，经过结点3，进行正向推理得到结点C的信息，

Bel(C=G)=m(WE=L,I=H)·m(C=G|WE=L,I=H)=1,

Bel(C=B)=m(WE=L,I=H)·m(C=B|WE=L,I=H)=0.

(4)HI和C结点的信息经过结点1进行正向推理得到TL的信息，

Bel(TL=H)=m(C=G,HI=H)·m(TL=H|C=G,HI=H)+m(C=G,HI=L)·m(TL=H|C=G,HI=L)=0.32·1+0.68·0=0.32,

Bel(TL=M)=m(C=G,HI=H)·m(TL=M|C=G,HI=H)+m(C=G,HI=L)·m(TL=M|C=G,HI=L)=0.32·0+0.68·0.8=0.544,

Bel(TL=L)=m(C=G,HI=H)·m(TL=L|C=G,HI=H)+m(C=G,HI=L)·m(TL=L|C=G,HI=L)=0.32·0+0.68·0.2=0.136

由此可得，态势威胁等级分别为高、中、低的信度为0.32，0.544，0.136。

3.2 基于联合信度参数的证据网络推理

(1)首先处理IFF结点传来的信息m(IFF=Y)=1,m(IFF=N)=0,将IFF的信息空扩展到IFF和NF的乘积空间上，再在结点4与联合信度参数进行融合，最后再边缘化到NF结点，计算步骤如下。

m(IFF=Y,NF=Θ)⊗m({NF=T,IFF=Y},{NF=T,IFF=N},)=m(IFF=Y,NF=T)=0.035,

m(IFF=Y,NF=Θ)⊗m({NF=T,IFF=Y},{NF=F,IFF=N})=m(IFF=Y,NF=T)=0.015,

m(IFF=Y,NF=Θ)⊗m({NF=F,IFF=Y},{NF=T,IFF=N})=m(IFF=Y,NF=F)=0.665,

m(IFF=Y,NF=Θ)⊗m({NF=F,IFF=Y},{NF=F,IFF=N})=m(IFF=Y,NF=F)=0.285

相同项加和得，

m(IFF=Y,NF=T)=0.035+0.015=0.05,

m(IFF=Y,NF=F)=0.665+0.285=0.95，

边缘化得，m(NF=T)=0.05,m(NF=F)=0.95。 共进行8次乘法运算，8次加法运算。

(2)NF结点与M结点的信息经过扩展后，在结点2处与联合信度参数融合，再经过边缘化得到HI的信息，此时2结点输入信息为m(NF=T,M=Y,HI=Θ)=0.05,m(NF=F,M=Y,HI=Θ)=0.95，同1)的步骤，分别计算得，m(HI=H,M=Y,NF=T)=0.035,m(HI=L,M=Y,NF=T)=0.015,m(HI=H,M=Y,NF=F)=0.285,m(HI=L,M=Y,NF=F)=0.665，边缘化得，m(HI=H)=0.32,m(HI=L)=0.68。共进行了32次乘法运算，30次加法运算。

(3)WE结点和I结点经过扩展后，在结点3处与联合信度参数融合，再经过边缘化得到C的信息，此时结点3输入信息为m(WE=L,I=H,C=Θ)=1,m(WE=L,I=H,C=Θ)=0，m(C=G)=1,m(C=B)=0。共进行16次乘法运算，16次加法运算。

(4)HI和C结点的信息经过扩展后，在结点3处与联合信度参数融合，再经过边缘化得到TL的信息，结点3的输入信息为m(HI=H,C=G,TL=Θ)=0.32,m(HI=L,C=G,TL=Θ)=0.68，m(TL=H)=0.32,m(TL=M)=0.544,m(TL=L)=0.136。共进行了8次乘法运算，和8次加法运算。

3.3 对比分析

由以上计算过程可知基于条件信度参数与基于联合信度参数的态势感知方法，在相同的先验知识的前提下，同样的信息输入得到的结果是相同的。但是先验知识存储量和计算量上存在着非常大的差别，先验知识存储量以存储向量的个数为计算参照，见表3。

表3 两种态势感知方法的对比

由表3可知，基于联合信度参数的态势感知方法随着先验知识中变量的增多，存储量呈指数增长，这样计算量也呈指数增长。而所提出的基于条件信度参数的态势感知方法在得到相同的结果的前提下，在计算量及先验知识存储量上远远优于基于联合信度参数的态势感知方法。

4 结 语

将基于条件信度参数的证据网络推理理论引入态势感知方法中，提出了一种基于条件信度参数的态势感知方法，解决了态势感知由于信息存储量大，计算步骤复杂而引起的问题，有一定的理论研究和工程应用价值，接下来将对基于条件信度参数的证据网络自动建模方法进行深入的研究。

[1] SHAFER G,SHENOY P P,MELLOULI K.Propagating Belief Functions in Qualitative Markov trees[J].International Journal of Approximate Reasoning,1987(1):349-400.

[2] MELLOULI K,SHENOY P.Qualitative Markov Networks[C]//Bouchon B,Yager R R(eds.).Uncertainty in Knowledge-Based Systems.Springer-Verlag Berl in Heidelberg,1987:69-74.

[3] PEARL J.Probabilistic Reasoning in Intelligent Systems:Network of Plausible Inference[M].San Mateo,CA:Morgan Kaufmann,Inc.,1988.

[4] WEBER P,MEDINA-OLIVA G,et al.Overview on Bayesian Networks Applications for Dependability,risk Analysis and Maintenance Areas[Z].Engineering Application of Artificial Intelligence,2010.

[5] 王双成.贝叶斯网络学习、推理与应用[M].上海:立信会计出版社,2010.

[6] 张连文,郭海鹏.贝叶斯网引论[M].北京:科学出版社,2006.

[7] 黄友平.贝叶斯网络研究[D].北京:中国科学院计算技术研究所,2005.

[8] 孙兆林.基于贝叶斯网络的态势估计方法研究[D].长沙:国防科学技术大学,2005.

[9] 郭百钢.基于Bayes网络的项目投资风险评估与决策方法研究[D].南京:南京理工大学,2004.

[10] 李海军,等.贝叶斯网络理论在装备故障诊断中的应用[M].北京:国防工业出版社,2009.

[11] SHENOY P P.Valuation-Based Systems:A Framework for Managing Uncertainty in Expert Systems[C]//Zadeh L A,Kacprzyk J(eds.).Fuzzy Logic for the Management of Uncertainty.John Wiley & Sons,NewYork,1992:83-104.

[12] SHENOY P P.Binary Join Trees for Computing Marginals in the Shenoy-Shafer Architecture[J].International Journal of Approximate Reasoning,1997,17:239-263.

[13] XU H,Smets P.Reasoning in Evidential Networks with Conditional Belief Functions[J].International Journal of Approximate Reasoning,1996(14):155-185.

[14] 李大鹏,雷肖剑,马国欣,等.基于证据网络的舰艇编队超视距反导态势评估[J].战术导弹技术,2014(1):50-54,85.

[15] PH.Smets.Belief Fuctions：the Disjuctive rule of Combination and the Generalized Bayesian theorem[J].International Journal of Approximate Reasoning，1993(9)：1-35.