基于脑磁信号的头部三维能量分布模型研究*

李 东 柳 渊 孙 伟 白 玫*

基于脑磁信号的头部三维能量分布模型研究*

李 东①柳 渊①孙 伟②白 玫①*

目的：通过分析处理脑磁数据，显示全脑三维能量分布，以期准确的反映脑部的神经活动情况。方法：选择小波函数对脑磁信号进行分析得到频域数据，将能量信息映射到与之对应的传感器位置，在传感器之间进行适当的插值，创建三维坐标下的补片，显示全脑三维能量分布。为验证方法的有效性，采集手指运动试验的脑磁数据，选取特定频率段，分析讨论不同时间下的地形图。结果：能量分布图反映的信息与运动事件相关同步研究的描述一致，即对侧初级运动区(M1)和双侧辅助运动区(SMA)会出现高能量信号，神经活动活跃。结论：该方法可以全面准确地反映大脑的神经活动情况，为分析大脑神经活动、确定神经活动源发位置提供了有价值的参考方法。

脑磁图；小波变换；地形图

[First-author’s address] Department of Medical Engineering, Xuanwu Hospital, Capital Medical University, Beijing 100053, China.

人体大脑产生的磁场包括两种，恒定磁场和交变磁场。恒定磁场由大脑内磁性物质产生，交变磁场则由神经细胞活动产生[1]。脑磁图测量大脑神经细胞内电流产生的相关磁场，由脑内神经椎体细胞的电生理活动所产生。磁信号穿透脑组织和颅骨有很少的衰减或没有衰减，与测量浅层细胞外电流靠容积传导的脑电图相比，脑磁图具有较高的空间分辨率[2]。脑磁信号比脑电信号对于大脑皮层表面的活动更加敏感[3]。在脑神经活动磁源定位的空间分辨率上，脑磁图优于脑电图[4-5]。脑磁图与脑电图相比有着噪声干扰小、信号采集优质及时间分辨率高等特点。近年来，脑磁数据被应用于神经外科术前定位和脑功能损伤评价等方面[6]。因此，对较为精准的脑磁信号进行分析，希望可以得到更加理想的处理结果。

1 脑磁信号处理方案

脑磁信号是非平稳信号，适合使用同时表达信号时域和频域特性的时频分析方法来处理。小波变换是典型的时频分析方法，其用小波函数移位和缩放得到一系列小波表示的信号。在信号分解过程中，小波函数不断平移、伸缩，使信号在各个频率层面上得到分解。频率从低到高，小波函数窗口会逐渐缩小。其分析结果在低频段拥有高频率分辨率和低时间分辨率，而在高频段有低频率分辨率和高时间分辨率。然而，小波函数在相当程度上影响变换的精准度和有效性。基于若干次先行试验，选取Morlet小波，其在时频分析处理脑电图(electroencephalogram，EEG)信号时经常被使用[7]。

采取的处理方案步骤：①采集原始脑磁数据；②信号的预处理，为去除接触噪声、基线漂移和工频干扰，对原始脑磁信号进行小波阈值法滤除噪声；③选取合适的小波函数及窗函数参数，对脑磁各导数据进行小波分析；④数据插值，计算功率分布；⑤生成能量分布的三维伪彩色图。而后还将引用1例手指运动试验数据对该方法有效性进行验证[8]。

2 三维头模型的建立

2.1 脑磁图系统传感器位置排布

所用数据是由颅外102信道探测阵列所采集。每组传感器测量三种数据，磁场强度、轴向梯度和曲面梯度。对于脑神经活动的浅表层图像绘制，曲面梯度数据要优于轴向梯度数据。而对于定位大脑深部的场源，场强数据优于梯度数据[9-10]。故使用磁场强度信号(如图1所示)。

图1 颅外102组传感器三维分布侧面图

2.2 数据插值方法

通过小波变换分析得到102组频率域数据。以其显示全脑能量分布略显单薄，因此进行适当的插值。基于大数据量，将三维表示化简为类似二维图像插值的处理方法。传感器在垂直轴方向分为7层排列，在相邻两层中各取相邻两点，4点上下相邻，组成一个栅格。如图2所示，A、B、C、D四点是相邻的4组传感器，其坐标分别为(xα，yα，zα)，α=A，B，C，D。X轴和Y轴方向插值数分别是n和m。

图2 数据插值图

位于4边上的插值点可直接根据4点坐标计算得出。而后，线性插值计算出AB间n个插值点Sj，同理可得图中的Tj，Pi，Qi，j=1，2，…n；i=1，2，…m。由此在栅格中形成一m*n的矩阵点集。计算出Pi与Qi之间第j个插值点Eij(公式1，公式2)。

式中j=1，2，…n。

式中i=1，2，…m，j=1，2，…n。

参数m和n的选择需适当。过小则插值不会发挥其填充数据缺失的作用，若过大则会导致程序运行缓慢。考虑插值点数与运行代价的关系，最终选择m=n=10[10]。插值后分布如图3所示。

图3 插值点俯视图

在空间位置上越邻近的点越有可能具有相似的特征值，这是空间插值技术中最基本的理论假设[11]。各种插值方法其共性是插值点幅值相当于对邻近的原始数据加权求和。据此建立第m个插值点能量幅值计算模型(公式3)。

式中fi是原始数据点幅值；d表示插值点与原始数据点之间的距离；c(d)是与距离相关的权重函数；计算邻近n个原始数据点的影响。

某点的能量强度对周边幅值的影响呈多种形态分布，这里取高斯分布，原始数据的能量幅值A可作(公式4)：

式中x为插值点与数据点间的距离。则插值点能量和相距d的数据点间的关系为(公式5)：

然而，某一插值点的能量值是原始数据点对其影响的总和。远距离的数据点对插值点的能量贡献甚微，可忽略，故取最临近的4个原始数据点计算。

使用MATLAB编写程序。创建补片，一个补片对象是由其顶点确定的多边形。如果坐标数据是不能定义封闭的多边形，将自动使多边形封闭。然而，如果单个补片面的边缘相互交叉，得到的面可能不会完全填充。此时，应将面分解为更小的多边形；补片色谱自动取伪彩色。

3 临床实验数据的处理

3.1 手指运动实验

手指活动激活对侧中央区和顶区皮层，皮层活动的10～25 Hz频率成分首先在-0.5～0.3 s时间段表现为功率抑制，接着有强烈的功率增强活动显示，最显著的功率增强集中在0.4～0.7 s区间[12]。事件相关功能磁共振成像显示初级运动区(M1)为运动执行区，手指运动对侧M1区明显激活，同侧则无明显激活区；辅助运动区(supplementary motor areas，SMA)、运动前区(premotor areas，PMA)、基底节及小脑皮质均为双侧激活[13]。基于上述研究，对三维能量分布的头模型进行实验验证。本研究实验数据来自首都医科大学宣武医院脑磁图室，为手指运动实验数据。被试手指为右利手，无手部骨关节疾病，无金属义肢、义齿，精神状态良好。实验中要求受试者保持安静，闭眼，尽量避免眼动、咬牙及皱眉等动作；左、右手食指分别平放在两个响应按键上；给予单耳纯音刺激，随机给予左、右耳刺激；根据听到的刺激，同侧食指做出按压键反应，其余手指不动。所用为右手运动数据。

3.2 结果分析

脑磁信号呈现特征节律波，可在枕部和感觉运动区记录到α节律和β节律，其节律表现出事件相关变化，若对脑磁信号进行频率域分析，可进一步了解大脑特定的活动机制[14]。试验数据采样频率1000 Hz，对刺激前0.1 s到发出指令后2.4 s给予关注。

α节律取10 Hz为代表频率，时间取第0.05 s、0.1 s、0.2 s、0.3 s、0.4 s、0.5 s、0.6 s、0.7 s、0.8 s、0.9 s和1.0 s。即指令发出前0.05 s到发出后0.9 s的数据。两图呈现能量的变化如图4、图5所示。

在0.05 s高能量信号分布在左侧中央沟、中央前回和中央后回区域，可理解是M1对应的部分。第0.1～0.6 s扣带回前部出现高能量分布，能量最高值出现在0.4～0.5 s，可理解其对应为双侧SMA。第0.7～1.0 s双侧SMA能量降低。指令发出之后，即0.1 s开始，能量开始逐渐增加，在0.4～0.5 s之间有显著的增加，0.5 s开始能量下降，持续至第0.6 s。第0.6 s开始显著下降。到第0.8 s，能量状态恢复至0.1 s之前。整个过程10 Hz节律活动最为强烈的时间是在指令发出后的第0.4 s。图5 f给出了10 Hz能量最值随时间变化的情况。大致可将其分为三个阶段：0～0.4 s，能量稍有升高；0.4～0.6 s，能量显著升高；0.6 s以后逐渐恢复[15]。

图4 10 Hz信号0.05～0.5 s时间点能量三维分布图

图5 10 Hz信号0.6～1.0 s时间点能量三维分布图

β节律取25 Hz，时间取第0.05 s、0.1 s、0.2 s、0.3 s、0.4 s和0.5 s。即指令发出前0.1 s到发出后0.4 s的数据。图6呈现β节律段25 Hz成分信号能量的全脑三维分布随时间变化的情况。同样开始时，高能量集中在对侧M1。之后的0.3 s内，高能量信号出现在双侧SMA，且能量值逐渐增大。到指令发出后的0.4 s，双侧SMA高能量信号减弱消失。0.1 s开始能量逐渐升高，这一趋势直至第0.5 s结束。

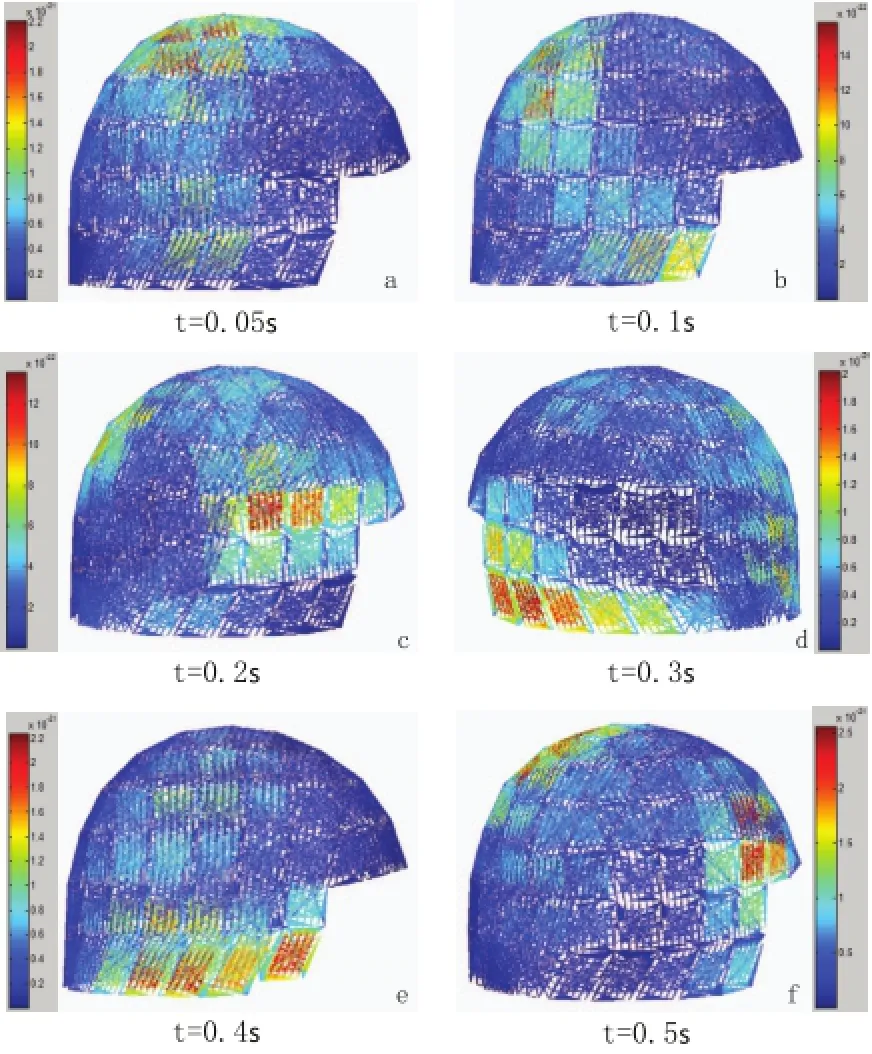
图6 25 Hz信号0.05～0.5s时间点能量三维分布图

文献研究显示，对于利手的运动事件相关变化，主要体现在对侧M1，双侧SMA及小脑的部分[15]。这与前述的分析讨论比较一致。

4 结论

皮层神经活动在时频域的能量分布情况可体现事件相关的皮层神经活动特征。本实验结果与有关文献对于手指运动的事件相关同步的若干研究情况相吻合[13-15]。采用三维考察脑部神经活动的方法，可观察三维空间中脑磁信号不同时间、不同频率下的能量分布地形图，以分析大脑的神经活动情况[16]。为分析大脑神经活动源发位置提供了较为有价值的观察方法。由于条件所限，本研究仍然存在某些问题，如能量分布图有明显的插值痕迹，插值方法有待改进。今后还需细化插值方式，提高程序运行速度，以设计出可视化的界面，提供更加细致的显示形式。

[1]韩建坤，康文巧.脑磁图简介[J].医疗装备，2004，17(8)：15-17.

[2]Ballief S，Mosher J C，Leahy R M.Electromagnetic brain mapping[J].IEEE Signal Processing Magazine，2001，18(6)：14-30.

[3]王建军.脑图和脑电图在癫痫中的应用[J].临床神经电生理学杂志，2005，14(3)：180-183.

[4]Cuffin BN.Effects of local variations in skull and scalp thickness on EEG's and MEG's[J].IEEE Transactions on Biomedical Engineering，1993，40(1)：42-48.

[5]Nicol'as VE，Carlos HM，Michael W，et al.Effect of head shape variations among individuals on the EEG/MEG forward and inverse problems[J].IEEE Transactions on Biomedical Engineering，2009，56(3)：578-596.

[6]吴婷，刘宏毅.脑磁图在神经外科术前定位的研究进展[J].现代电生理学杂志，2011，18(2)：102-105.

[7]张萍，黄庆.脑磁图表现对脑卒中患者脑功能损伤程度和区域的评估价值[J].中国临床康复，2004，8(34)：7650-7651.

[8]吴国材，李梅，吴南，等.脑磁图、视频脑电图在癫痫术前评估中的应用[J].第三军医大学学报，2009，31(11)：1080-1083.

[9]崔骊，李向东，云庆辉.心脑电图机测量结果的不确定度分析评定[J].中国医学装备，2013，10(6)：26-27.

[10]柳渊，孙伟，严汉民，等.癫痫患者脑磁图的高频振荡量化算法研究[J].中国医学装备，2012，9(11)：1-3.

[11]Zygierewicz J，Sieluzycki C，Konig R，et al.Eventrelated desynchronization and synchronization in MEG：Framework for analysis and illustrative datasets related to discrimination of frequency-modulated tones[J].J Neurosci Methods，2008，168(1)：239-247.

[12]邬伦，刘瑜，张晶.地理信息系统原理方法和应用[M].北京：科学出版社，2005：178-192.

[13]侯文生，李卫娜.Jiang Yingtao，等.手指活动相关脑磁图的时-频域特征分析[J].仪器仪表学报，2009，30(10)：2093-2098.

[14]李恩中，韩璎，翁旭初，等.事件相关功能MRI在随意运动脑功能活动区协同作用研究中的应用[J].中国放射学杂志，2002，36(5)：397-401.

[15]Pollok B，Gross J，Schnitzler A.How the brain controls repetitive finger movements[J].Journal of Physiology-Paris，2006，99(1)：8-13.

[16]于薇，林冲宇，臧玉峰，等.利手和非利手随意运动的全脑功能磁共振成像[J].中国放射学杂志，2003，37(5)：402-405.

Research on head three-dimensional energy distribution model based on brain magnetoencephalography signal processing

/
LI Dong, LIU Yuan, SUN-Wei, et al// China Medical Equipment,2014,11(10):8-11.

Objective: A three-dimensional energy distribution over the whole brain will be displayed by analyzing the brain magnetic data, so as to reflect the neurological activity of the brain accurately. Methods: The brain magnetic signal was processed with wavelet function to get frequency domain data. The energy information is mapped to the corresponding sensors’position. In order to show the energy distribution, the author interpolated between sensors, created three-dimensional patches. For the purpose of validating, MEG data from a finger exercise testing subject was analyzed. Moreover, data of particular frequency was discussed also. Results: What it shows is consistent with description on event related synchronization. Actually the movements activated contralateral primary motor cortex (MI), bilateral supplementary motor area (SMA). Conclusion: Because of reflecting neurological activity accurately, it is said this method provides a valuable reference to analyze brain activity and locate neural activity.

Magnetoencephalography; Wavelet transform; Topographic map

1672-8270(2014)10-008-04

R831

A

10.3969/J.ISSN.1672-8270.2014.10.003

2014-06-26

国家自然科学基金(81171229)“应用脑电磁信号频段分解对癫痫病人脑皮层中央区振荡规律的研究”

①首都医科大学宣武医院医学工程处 北京 100053

②首都医科大学宣武医院神经内科 北京 100053

*通讯作者：jswei65@163.com

李东，女，(1987- )，硕士，助理工程师。首都医科大学宣武医院医学工程处，研究方向：医学信息分析与处理。