基于参数平面的自适应调和纹理映射算法

王 莹,王延杰,周渝人.2,李静宇,姚志军

(1. 中国科学院 长春光学精密机械与物理研究所， 吉林 长春130033；2. 中国科学院大学，北京100049)

1 引 言

纹理映射是一门广泛应用于计算机图形学中的技术，尤其是在大型虚拟仿真系统增加虚拟模型真实性方面。最简单的纹理映射为定义纹理图片的4个顶点坐标(u,v)与模型相应的4个顶点坐标绑定，将纹理图片直接覆盖到模型的表面。对于简单模型可以起到增加虚拟模型真实性的目的，对于复杂度较高的模型我们常用的方法是调和纹理映射[1-9]。即借助一个参数化平面，通过指定模型与纹理相对应的特征点将纹理图片调和映射到模型的指定位置。

国内外对于调和纹理映射具有代表性的工作有：文献[2]能够处理任意特征的多边形纹理映射，将形变作为目的函数，该算法仅在特征点较少时可以保持纹理的有效性。文献[3]为ABF(Angle-Based Flattening)基本算法，在模型映射到二维平面过程中保持角度的变形性最小，该算法可能导致长度形变或者面积形变的增大。文献[5]是基于ABF算法旨在减少由ABF算法引起的长度形变。文献[6]预先对模型进行参数化，可保持纹理的有效性，算法复杂度高效率较低。

本文针对经典算法在保持纹理有效性的情况下算法复杂度高效率低的问题，提出了一种自适应选取目标函数的调和纹理映射方法。通过将三维模型映射到二维参数平面，在纹理图片及参数平面上设定相对应的特征点，并分别三角化。对于模型三角化后的每一个三角块分别计算其内部所有顶点的评估值，并将评估值的平均值与阈值σ1、σ2相比较。根据比较结果的不同选择不同的目标函数来计算非特征约束点的纹理坐标值。

实验表明本文算法可以保持纹理的有效性，且算法的复杂程度低计算时间短。

2 参数化处理

首先给出自定义参数：

fii=1,2.....n表示三角形面片序列。其中n为网格模型中三角形的总个数。

Nkk=1,2....m为节点序列。m为网格模型内部节点个数。

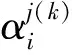
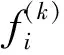
S2DArear(fi)，S3DArear(fi)为面片fi分别在参数平面和三维网格模型上的面积。

如图1所示分别为人脸模型的三维网格模型和相应的参数平面。

图1 三维网格模型Fig.1 3D mesh model

我们利用Sheffer[4]介绍的4个约束条件来快速判断平面化三角形的有效性。即：

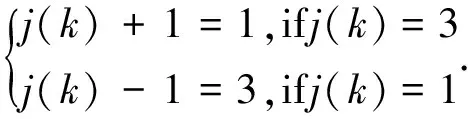
约束条件(1)保证了三角形的朝向，即防止三角形翻转的发生，(2)保证了每个三角形面片的有效性。约束条件(3)保证在一个顶点周围所有的三角形必须处以同一个平面，并且和条件(4)一起保证了参数平面在拓扑结构的合理性。

三维网格模型映射平面过程中，处于深度z不同的边极易发生交叉。对于这样的边，考虑算法的复杂度将不再计算与这条边所关联的三角形的变形程度。

对参数平面和纹理图片分别指定相对应的特征点，特征点的个数视模型细节程度而定。根据特征点的位置分别进行Delaunay三角化，将三角化后的块分别记为Mi，Pj。其中i,j分别表示参数平面和纹理图片三角化后块的序列。如图2所示为三维模型及平面参数后的效果图。图3所示为已标定特征点[10]纹理图像及特征点三角化后的图片。

图2 参数平面特征点Fig.2 Feature points on parameter plane

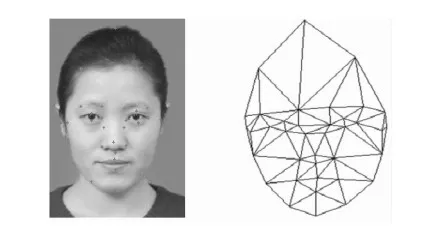
图3 纹理图片特征点及三角化Fig.3 Feature points on texture image and triangulation

设函数

i=1...x.

(1)

为评估函数。其中：x表示顶点NK处的三角形的个数。ρ1，ρ2(ρ1,ρ2>0)为权重值。第一部分表示顶点NK相关的所有三角形面片在参数平面上的面积和与在原始网格上面积和之比；第二部分表示顶点NK相关的所有角在参数平面上角度与原始网格上角度差的平方和与在原始网格模型上角度平方和之比。对于不同的模型可以改变ρ1,ρ2的值以使角度和三角形面积对映射产生不同的影响。本文算法实验中ρ1,ρ2均取值为0.5。

对于三角化后的参数平面计算Mi的所有内部顶点的评估值Ei,i=1...mi(mi为三角块Mi内部顶点的个数)，给定一个阈值[11]σ1，σ2(0<σ1<σ2)。当表达式E(Mi)=∑Ei/mi<σ1时我们将这种情况记作：A(轻微变形区域)；当E(Mi)=∑Ei/m>σ2，记作：C(剧烈变形区域)；当E(Mi)=∑Ei/m处于(σ1，σ2)之间时记作：B(适度变形区域)。

3 调和映射

对于非特征点纹理坐标的计算，在过去的研究中主要有保持角度形变最小和保持边形变最小两种映射算法。

3.1 保角映射

Sheffer[3]提出一种保角的参数化方法ABF，通过保持三维网格模型和参数化后网格上对应网格点所依附边角度分布的一致，求解一个关于角度的目标函数。

(2)

其中:λ,μ,v为权重值。

我们只需将模型和纹理图片上的指定的特征点代入公式(2)，通过最小化该目标函数得到一个角度矩阵。根据已知的特征点坐标和相应的角度三角函数值计算其余点的纹理坐标值。

由于该算法在变形比率比较大的网格曲面上可能引起长度形变或者面积形变，但是其适用范围广泛不必预先定义边界，因此在本文算法中对于情况A我们采用保角映射算法计算非约束点的纹理坐标值。

3.2 边变形最小

对于剧烈变形区域即C类情况我们采用边变形最小来计算非特征约束点的纹理坐标。目标函数如式(3)所示：

(3)

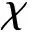
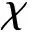
将已知设定特征点的坐标代入公式(3)，其余的非特征点的坐标值通过解公式(3)的最小值得到。

公式(3)中第一部分表示纹理映射坐标与原始顶点坐标的偏离程度。第二部分主要影响映射区域的光滑程度。在本文算法中ε取0.45映射效果最好。

(3)对于情况B我们将三角形块继续分块，对每个小三角形面片同样计算其内部所有顶点的评估函数值[12]。用评估函数和的均值跟阈值ρ1,ρ2相比较判断每一个小块采用哪种目标函数。即迭代思想，通常只需迭代一到两次即可。

4 实验结果分析

实验环境为 Pentium(R) dual-Core CPU E5300 2.6G，内存为2G，操作系统Microsoft Windows XP，Inter(R) G33/G31显卡，编程环境为VC++2010调用OpenGL。在实验结果比较中以MinE代表边变形最小算法。

由于我们采用分块映射的方法在不同三角块之间的边界顶点极易出现计算得到的纹理坐标不一致的纹理，对于这种情况我们采取取平均值的方法确定边界的纹理坐标值。

如图4所示为本文算法将人脸照片映射到脸部模型上的映射效果图。

图4 人脸模型映射效果Fig.4 Mapping results of Face model

可以看出人脸照片五官都正确地映射到脸部模型的五官位置上，说明本文算法将纹理图片正确的映射到了三维模型上。但是不难发现鼻子处纹理映射位置不够精确。局部映射效果如图5所示。对于局部特征点周围的纹理坐标映射不精确的问题，我们采用文献[7]的自适应局部邻域调整方法。只调整顶点vi以及距离vi较近的一阶或者二阶顶点的纹理坐标值,原则为移动局部顶点的位置但不影响整体的拓扑结构。考虑算法复杂度这里我们只计算到顶点vi的二阶领域的顶点的纹理坐标值。

图5 局部纹理Fig.5 Local texture

如图6(a)所示，当调整鼻子周围4个特征点的纹理坐标值时，依次计算4个特征点的一阶领域顶点的变化量Δt(t阶领域顶点纹理坐标调整前后的变化量)。若小于提前定义的阈值Δθ则停止计算，否则计算其二阶顶点的纹理坐标的变化量。图6(b)所示为调整4个特征点纹理坐标值后的效果图，图6(c)为从不同观察角度看到的效果图。算法中只计算了4个特征顶点的一阶领域点的位置。

(a)局部顶点(a) local vertex

(b)调整后侧视图 (c)局部调整后正视图(b) side view after the adjustment (c) front view after the adjustment图6 局部顶点位置调整后效果图Fig.6 After adjust the local vertex position

对于映射完毕的三维模型我们采用拉普拉斯光滑算子来平滑映射效果。

(a)猫头面具 (b)老虎纹理 (c)映射效果图(a) owl mask (b)tiger texture (c)After mapping图7 猫头面具映射效果图Fig.7 Mapping results of owl mask

(a)鱼模型 (b) 纹理图片 (a)Fish model (b) Texture map

(c)右视图 (d)左视图(c)Right side (d) Left side

(e)正视图 (f)棋盘格图片映射效果 (e) Front view (f)Checkerboard mapping

(g)ABF映射效果 (h)边变形最小映射效果 (g) ABF mapping (h) MinE图8 鱼模型映射效果图Fig.8 Mapping results of fish model

如图7所示为猫头面具模型映射老虎图片的效果图。图7a、b所示分别为猫头面具的三维网格模型，相应的纹理图片，图7c为本文算法处理后的映射效果图。由图可以看到老虎的鼻子精确映射到了猫头面具的鼻子上。因为本身模型的特征点较多算法计算时间较长，所以对于猫头面具的胡须和尖牙我们采用默认纹理映射。

如图8(a)、(b)分别为鱼的三维网格模型和相应的纹理图片。图8(c)、(d)、(e)为本文算法将纹理图片映射到三维模型上在不同观察位置的效果图。图8(f)为本文算法以相同的纹理坐标将黑白相间的图片映射到模型上的效果图，图8(g)为保角映射算法映射效果图，图8(h)为边变形最小算法映射效果图。由图中可以明显看到保角映射算法和变形最小算法在鱼脊处纹理明显失真，且保角映射算法失真度更大，而本文算法没有使纹理图片失真，由此可知本文算法优于经典算法。

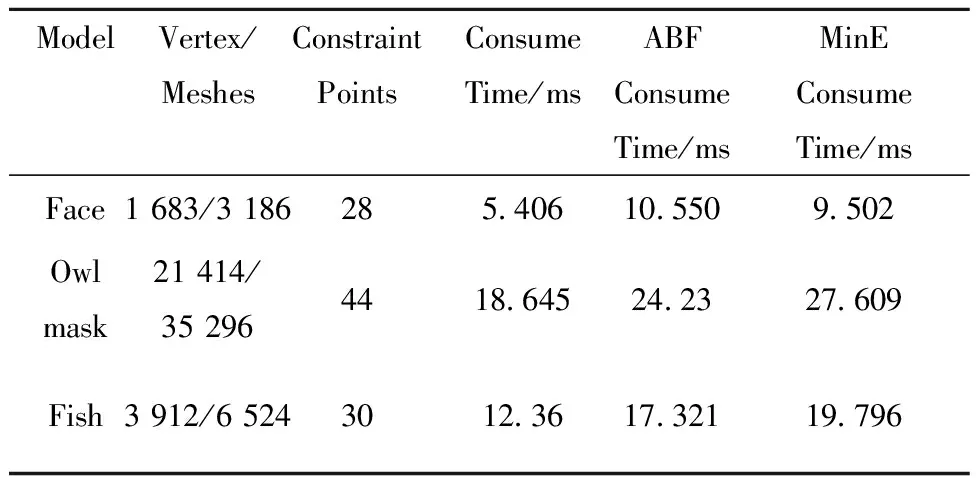
表1 实验数据

表1分别为脸部模型、猫头面具模型和鱼模型顶点/面片个数、约束点个数和算法运行时间的具体信息。由表1可知本文算法在计算时间上较经典算法有明显提高，平均提高75%以上，并且本文对多个模型进行多次实验并将纹理映射后的模型加载到帧频高于100帧/s的实时渲染系统中，发现本文算法可以很好地保持纹理的有效性。

5 结论与展望

提出了一种根据分块三角形内部顶点的评估函数平均值选择目标函数的纹理映射方法。分析了映射过程中出现的问题并给出了有效的解决方法。在保持整体拓扑结构不变的同时调整局部顶点的坐标来解决局部映射不精确的问题。实验证明本文方法具有以下优点：

(1)鲁棒性好。因为通过将本文算法映射后的模型加载到高帧频实时渲染系统中，发现本文算法能够保持纹理的有效性。

(2)交互性简单，整体性强。本文算法只需指定模型与纹理图片上相对应的特征顶点即可，不需要额外的人工交互；并且算法是针对整个网格模型进行操作，避免了单独分块处理产生的边界变形问题。

(3)算法速度快、效率高。只需要计算内部顶点的评估值，通过评估值与阈值的比较自适应的选取目标函数即可，相较于经典映射算法时间复杂度平均提高75%以上，所以即使是对大型网格模型也具有很高的计算效率。

调和纹理映射目前都需要交互选取特征顶点并分块映射到网格模型中，对于复杂度高的模型特征点相对多，算法复杂度也就会提高，因此如何根据细节特征自动检测选取特征点，从而提高算法的易操作性是下一步要攻克的主要难题。

[1] Bruno L,Jean L M.Non distorted texture mapping for sheared triangulated meshes [J].Proc.ofSgigarph98，1998,6(3):343-352.

[2] Bruno L.Constrained texture mapping for polygonal meshes [J].EngineeringwithComputers,2001, 11(5):679-689.

[3] Sheffer A,de Sturler E.Parameterization of faceted surfaces for meshing using angle-based flattening [J].Enginee-ringwithComputers,2001,17(1): 326-337.

[4] Alla S T, de Eric T. Smoothing an overlay grid to minimize linear distortion in texture mapping [J].ACMTransactionsonGraphics,2002, 21(4): 874-890.

[5] Kraevoy V, Sheffer A, Gotsman C. Matchmaker: constructing constrained texture maps [J].ACMTrans.Graphics,2003,22(3): 326-333.

[6] Guo Y W, Pan Y J,Cui X F,etal.Harmonic maps based constrained texture mapping method [J].JournalofComputerAidedDesign&ComputerGraphics,2005,7(17): 1358-1370.

[7] Lee T Y, Yen S W, Yeh I C. Texture mapping with hard constraints using warping scheme [J].TransactionsonVisualizationandComputerGraphics,2008,14(2): 382-395.

[8] Se′bastien H, Anatole L, Tony R,etal.Design and application of real-time visual attention model for the exploration of 3D virtual environments [J].TransactionsonVisualizationandComputerGraphics,2012,18(3): 356-368.

[9] Yu H C, Lee T Y, Cheng Y,etal.RBF-based reparameterization method for constrained texture mapping [J].TransactionsonJournalName,2012,8(2): 785-796.

[10] 丁南南, 刘艳滢, 朱明.尺度相互作用墨西哥帽小波提取图像特征点[J].液晶与显示,2012,27(1):125-129.

Ding N N, Liu Y Y, Zhu M. Extracting image feature points using scale-interaction of mexican-hat wavelets [J].ChineseJournalofLiquidCrystalsandDisplays,2012,27(1): 125-129.(in Chinese)

[11] 吴一全，孟天亮，王凯.基于斜分倒数交叉熵和蜂群优化的火焰图像阈值选取[J].光学精密工程,2014,2(1):235-243.

Wu Y Q, Meng T L, Wang K. Threshold selection of flame image based on reciprocal cross entropy and bee colony optimization [J].Opt.PrecisionEng.,2014,2(1):235-243. (in Chinese)

[12] 杨利红，赵变红，张星祥,等.点扩散函数高斯拟合估计与遥感图像恢复[J].中国光学,2012,5(2):181-188.

Yang L H, Zhao B H, Zhang X H,etal.Gaussian fitted estimation of point spread function and remote sensing image restoration [J].ChinesOptics,2012,5(2):181-188.(in Chinese)