砂土中边坡附近单桩水平抗力的模型试验研究
2014-02-04高博雷张陈蓉张照旭
高博雷 ,张陈蓉 ,张照旭
(1.同济大学 地下建筑与工程系,上海 200092;2.同济大学 岩土及地下工程教育部重点实验室,上海 200092;3.中国石油西气东输管道公司,上海 200122)
1 引 言
目前水平受荷桩的研究主要针对地表水平的情况,然而实际工程中,由于堤岸、冲刷等因素存在会出现水平受荷单桩基础布置在边坡附近。与平地不同,边坡存在对桩基水平变形受力有明显的削弱作用。在设计中如何评估边坡对水平受荷桩的承载影响,是非常值得探讨的问题。
p-y 曲线是研究水平受荷桩桩土非线性相互作用最常见的方法,并被美国石油协会API 规范[1]采用。Kim 等[2]建议,采用双曲线形式来模拟桩侧p-y 曲线表达式。Reese 等[3]由大型现场原位测试分别提出了砂土中浅层和深层单桩p-y 曲线,采用应变楔模型得到浅层土体极限抗力 pu值。朱斌等[4]开展了干砂和饱和砂土中大直径单桩静载和循环荷载离心模型试验,在修正初始刚度的基础上获得相应静载双曲线p-y 曲线表达式。Zhang 等[5]研究了砂土中桩侧极限抗力的产生机制,认为极限抗力由桩前土抗力和桩-土界面摩擦力两部分构成。针对边坡对水平受荷单桩的影响,Mezazigh 等[6]开展了砂土中边坡附近单桩p-y 曲线变化的离心试验,揭示了边坡对浅层地基的影响规律。Georgiadis 等[7]采用三维有限元数值模拟得到黏土不排水条件下边坡附近单桩p-y 曲线,并导入商业地基反力程序分析了边坡中单桩水平承载特性。由此可知,众多研究都集中在平地条件下的桩侧静载p-y 曲线,针对存在边坡的情况研究成果非常有限,并且主要还是黏土地基。
本文通过物理模型试验,开展了边坡存在对水平受荷单桩桩侧抗力影响的试验研究,探讨了边坡坡角和边坡到桩的距离对单桩弯矩分布和桩侧p-y曲线的影响。在试验基础上,修正桩侧极限土抗力和初始刚度,提出了砂土中边坡附近浅层区域单桩双曲线p-y 曲线修正公式,并与离心模型试验结果进行了对比验证。本文工作为边坡附近的桩基设计提供依据。
2 试验方案
2.1 地基土的制备
将河沙晾晒后过筛,去除粒径1 mm 以上颗粒杂物,进行颗粒筛分试验得到砂土的级配曲线如图1 所示。Oversen[8]提出,模型试验中桩径与d50(小于该粒径的土粒质量占土的总质量的50%的粒径)的比值大于40 时可以忽略模型土的尺寸效应,从级配曲线看,试验用砂 d50大约为0.15 mm,试验用桩桩径D=25 mm,D/d50大约为160,远大于40。采用落雨法制备土样,试验完成后取土样进行基本参数测定,结果见表1,为中密砂。
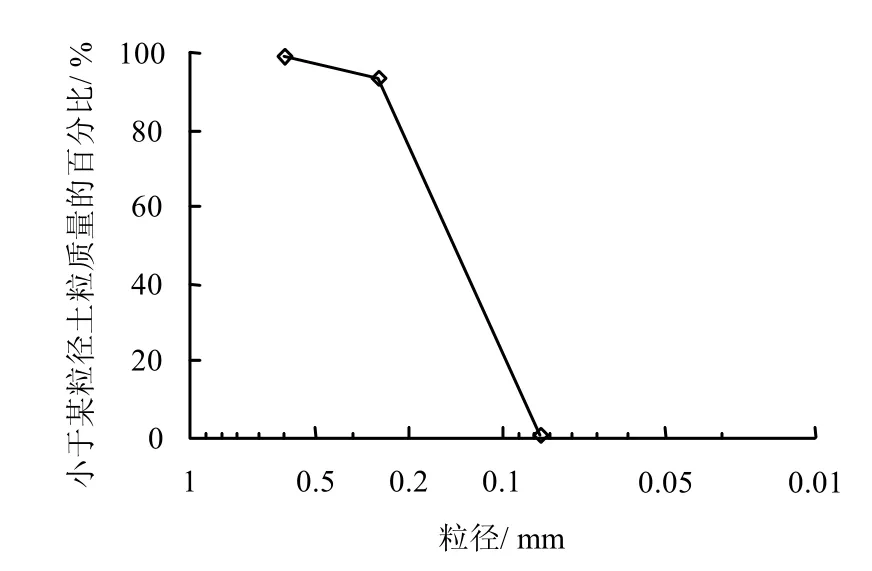
图1 试验用砂颗分曲线Fig.1 Calibration curve of relative density for test sand

表1 模型试验用砂基本参数Table 1 Parameters of sand in tests
2.2 模型桩的制作
模型桩由ABS 空心塑料管加工而成,弹性模量为2.51 GPa,泊松比为0.39。桩顶和桩端用铝合金块封闭。桩身上布置一金属圆环,用于施加水平荷载。模型桩与原型桩的长度相似比关系为1:80,依据桩的柔度系数确定单桩壁厚。模型桩与原型桩的尺寸对应参数见表2。
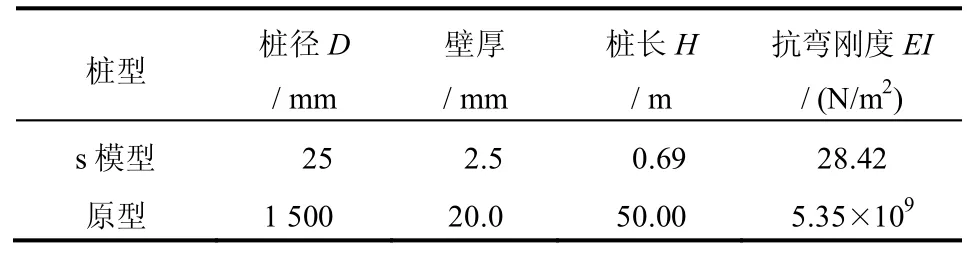
表2 模型桩与原型桩参数Table 2 Parameters of model and prototype piles
将模型桩对半剖开,在桩的内壁入土部分沿桩长均匀布置10 对测量弯矩的应变片(见图2)。在桩顶下方3 cm 处设2 个直径10 mm 的圆孔,引出应变片连接线。采用悬臂梁法标定加工完成模型桩的弹性模量以及应变片系数,标定结果见图3,材料弹性模量取4 组数据平均值为2.51 GPa。
2.3 试验布置与加载
试验区域(长×宽×高)为1 m×1 m×1 m,试验采用的水平荷载加载方式以及边坡和单桩的相对位置关系示意图如图4 所示。为消除边界效应,桩与箱壁距离大于8D,桩端与箱底距离大于4D。

图2 模型桩身应变片布置(单位:mm)Fig.2 Instrumented model pile(unit:mm)
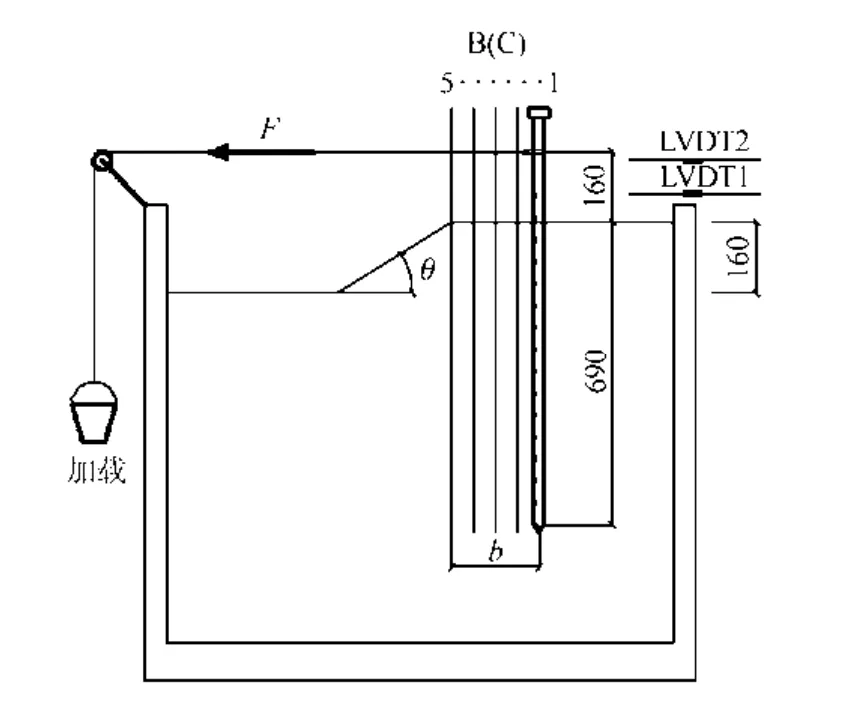
图4 加载示意图(单位:mm)Fig.4 Loading diagram(unit:mm)
用固定于模型箱框架上的定滑轮施加桩顶水平荷载,加载高度控制在泥面以上160 mm。每级加载用电子天平称量400 g 砂缓慢倒入桶中,最后一级荷载下出现位移明显增大,停止加载。桩顶布置2 个LVDT 位移传感器,用以监测桩顶的位移和转角边界条件。使用YE2539 应变采集仪采集桩身应变。
2.4 试验方案
为研究边坡存在对水平受荷单桩变形受力的影响,共进行了11 次试验,分为3 组。分组依据为边坡坡角θ 的大小以及桩到边坡坡顶距离的远近b。A组为基准试验,对应平地无边坡的情况。B 组(B1~B5)试验边坡坡角为32°,与试验砂土的内摩擦角相等;C 组(C1~C5)试验边坡坡角为20°。试验中埋深和加载高度均相同,B和C 组边坡高度为160 mm,分组明细见表3,图4 中B(C)、1~5 表示各组别模型桩位置。

表3 试验分组表Table 3 Grouping of test
3 试验结果分析
3.1 数据处理方法
为获得水平受荷单桩沿着深度的响应,试验研究多采用高次多项式[9-10]对实测应变值进行沿桩长的拟合,得到分布函数 ε(z)。对应变拟合值分别进行2 次积分和求导获得桩身位移y(z)和桩侧土压力 p(z)[6],表达式为

式中:ε为应变;r为曲率半径;z为深度M(z)为对应深度z 处的弯矩;EpIp为桩的抗弯刚度;E、F为积分常数,由桩顶边界条件确定。实践发现,高次多项式的拟合易引起求导积分过程中的奇异拐点,数据无法用于分析。为解决该问题,本次试验采用了分段3 次多项式对实测应变数据进行拟合,改善了数据的光滑程度,效果见章节3.2。
3.2 A 组试验承载变形特性分析
图5~7为A 组基准试验中水平受荷单桩在各级荷载下的桩身弯矩、位移以及桩侧土反力分布。为验证分段3 次多项式数据拟合的合理性,对图7的桩侧土抗力进行积分得到桩顶水平荷载,发现与实际加载误差在10%以内,并且桩身位移曲线和桩侧土反力曲线的第一零点位置在荷载等级较小时都比较吻合。由于积分深层累积误差较大,导致荷载较大时0 点位置有偏差。由图7 可知,桩身最大弯矩作用点随着荷载的增大而出现下移趋势(如图5中虚线所示),从4D 逐渐发展到6D,说明浅层土体逐渐达到了极限抗力。
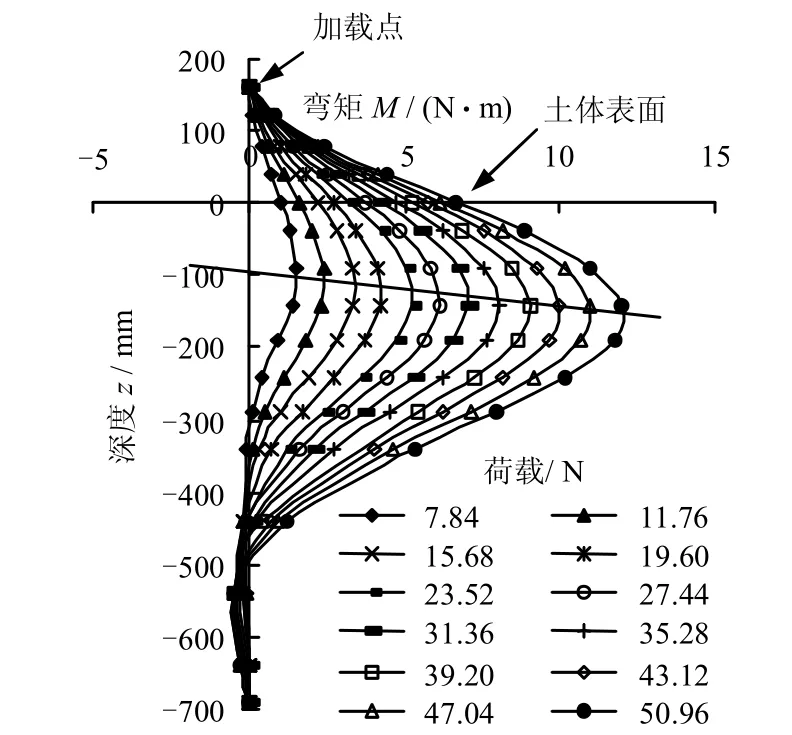
图5 桩身弯矩分布曲线(A 组)Fig.5 Bending moment curves(group A)
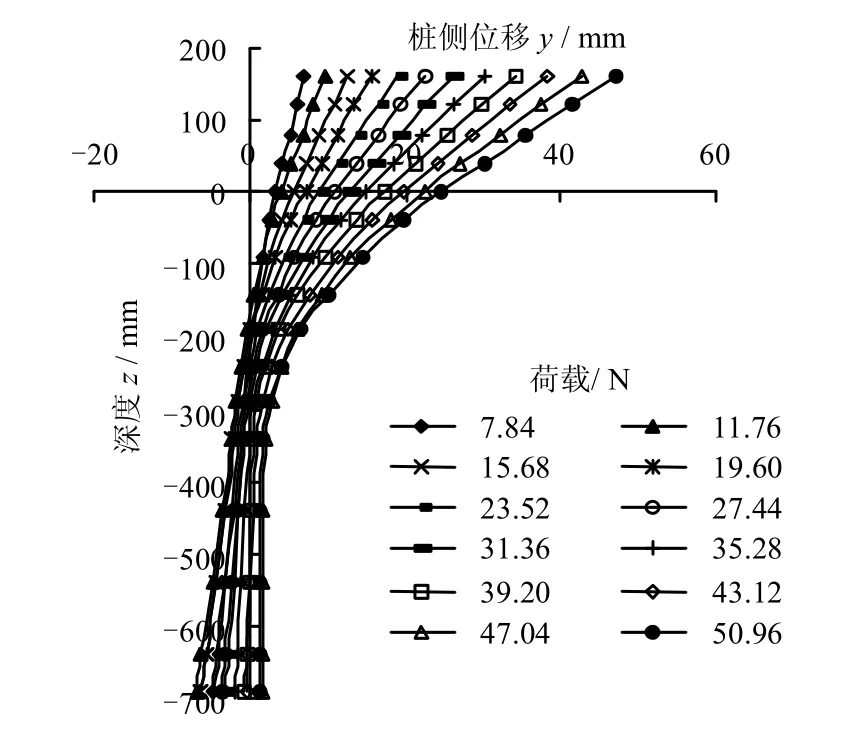
图6 桩身位移分布曲线(A 组)Fig.6 Displacement curves(group A)

图7 桩侧土抗力分布曲线(A 组)Fig.7 Lateral resistance curves(group A)
常用的双曲线p-y 曲线[2]表达式为
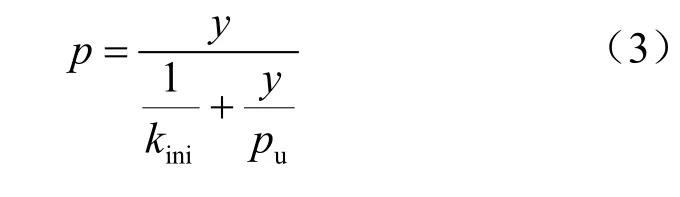
式中:kini为初始刚度;pu为桩侧极限抗力。API规范[1]给出砂土中桩侧极限土抗力计算公式为
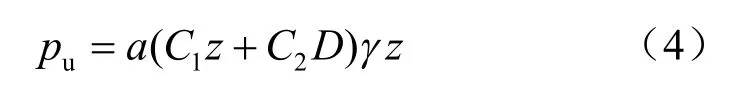
式中:C1、C2分别为与砂土密实度及内摩擦角相关的系数,查表确定;D为桩的外径;z为深度;γ为土体重度;a为与深度相关的修正系数,a=
朱斌等[5]基于砂土中大直径单桩模型试验认为桩侧p-y 曲线初始刚度 kini与深度z 呈非线性关系:

式中:初始地基反力系数 nh与砂土的密实度、桩的打入方式以及桩头约束等条件有关;β为经验系数,建议取值0.7,其他符号意义同前。
图8为A 组试验得到的砂土中水平受荷单桩p-y 曲线以及浅层土体中API规范p-y 曲线和双曲线p-y 曲线。
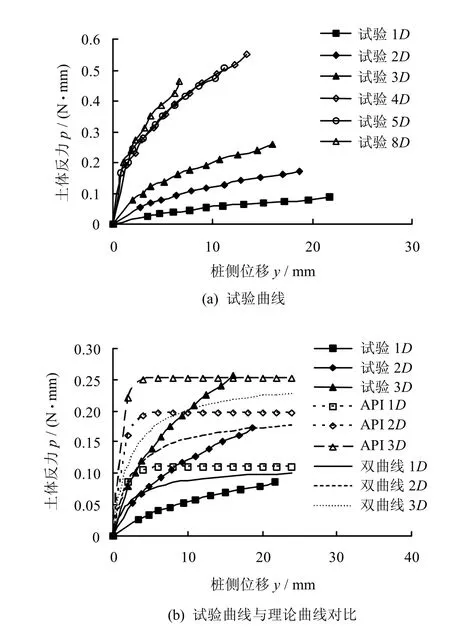
图8 不同深度处的p-y 曲线Fig.8 p-y curves of different depth
由 8(a)试验曲线可见,浅层1D、2D和3D 深度,p-y 曲线的初始刚度和极限抗力随着深度增加明显,而4D、5D、8D 深度对应的p-y 曲线刚度值趋于稳定。对比图8(b)浅层API 规范p-y 曲线和双曲线p-y曲线可知,API 规范计算的初始斜率误差较大,而采用朱斌等[5]得到的双曲线p-y 曲线与试验值更加接近。
3.3 边坡对水平受荷单桩的影响
图9为A、B 两组试验桩顶水平荷载-位移曲线。分别对应无边坡情况和边坡倾角θ=32°,桩与坡顶距离0D、2D、4D、6D、8D 的5 种情况。由图可见,边坡的存在减小了荷载-位移曲线的刚度,曲线偏离A 组基准试验值(无边坡),随着桩与边坡距离b 的增大,边坡影响逐渐减弱。同样的荷载条件下,b=0D时的桩顶位移最大,而增大至b=6D和8D,荷载较小时,有、无边坡存在对p-y 曲线影响可忽略不计。θ=20°时组试验得到与此类似规律,但差异有所减小。

图9 不同临坡距下的水平荷载-位移关系(B 组,θ=32°)Fig.9 Load-displacement curves(group B)
图10为B 组试验(边坡坡角32°),桩与边坡距离b=0D、2D、4D、6D和8D 5 个单桩位置,所对应的桩顶水平荷载与A组无边坡时桩顶荷载的比值区间(水平位移相同条件下)。
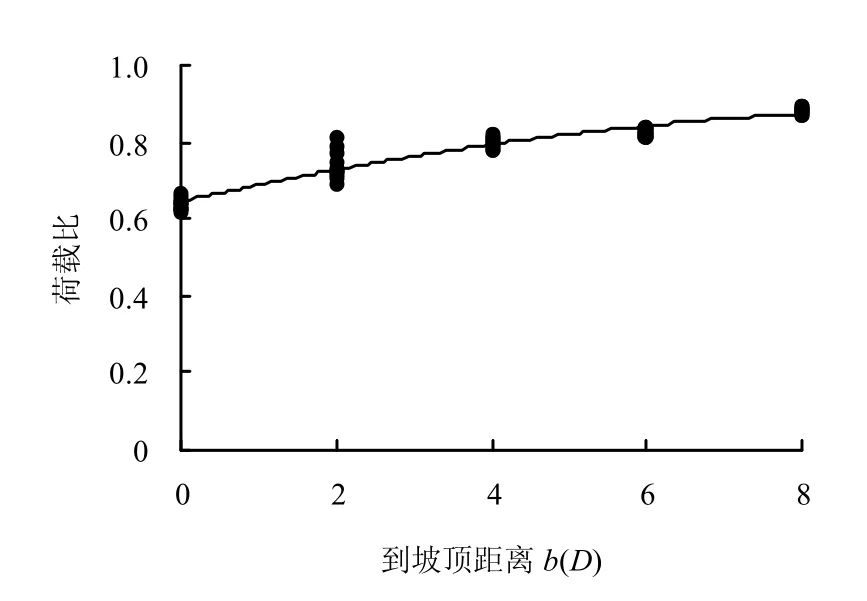
图10 水平承载力荷载比(B 组,θ=32°)Fig.10 Load ratio line(group B)
从图10 中可以发现,当b=8D 时,荷载比基本稳定在0.9,从b=4D 降至b=0D,荷载比从0.85下降到0.6 左右,显然边坡存在对这一距离段最为敏感。
图11为C 组试验(边坡角度20°),桩顶水平荷载为39.2 N 时,距离边坡不同距离处的单桩桩身弯矩沿着深度的分布曲线。由图可见,离边坡越近,最大弯矩位置越深,变化趋势如图中虚线所示。从平地的0.2L 降至b=0D 时的0.28L(L为桩长),且b=0D 时的桩身最大弯矩值比平地大25%左右。对B 组试验(边坡角度为32°)进行类似分析,得到桩身最大弯矩的位置与C 组基本一致,但最大值比平地时大约30%。随着边坡与单桩距离减小,桩身最大弯矩的位置下降以及量值增加,说明浅层土体的抗力变小,荷载逐步向深处传递,土体中达到极限抗力的区域呈扩大趋势。鉴于此,本文下面进行了相关的探讨。

图11 桩身弯矩曲线(C 组)Fig.11 Bending moment curves(group C)
3.4 考虑边坡影响的pu值
由前文分析认为(见图8),模型试验得到了浅层3D 范围内水平受荷桩的桩侧土抗力极限值。表4和表5 分别给出了B 组和C 组试验中边坡附近单桩在1D、2D、3D 深度处桩侧极限抗力 pu的试验值,以及平地条件下A 组试验值和API 规范计算值。
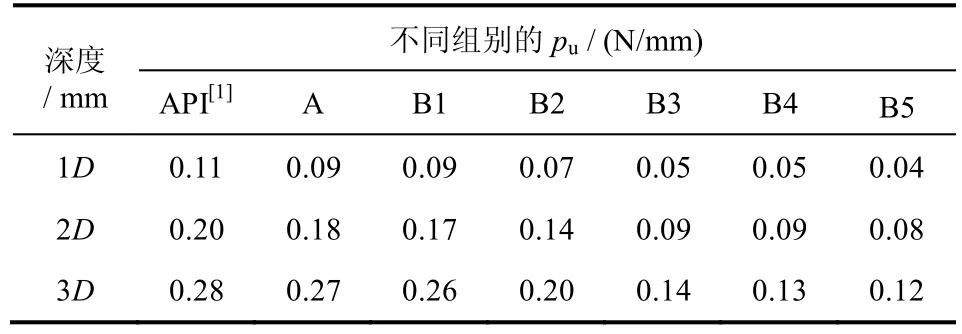
表4 B 组试验中pu值对比Table 4 Comparison of pufor group B
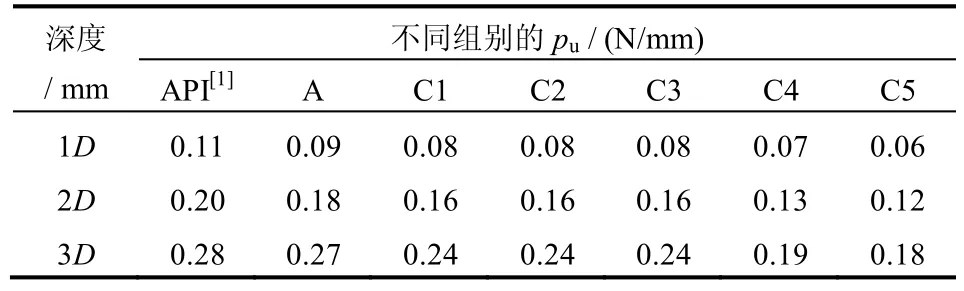
表5 C 组试验中pu值对比Table 5 Comparison of pufor group C
为了得到边坡角度和单桩位置对桩侧极限抗力pu值的影响,绘制了归一化的桩侧极限抗力值和桩与边坡距离关系的折线图,如图12 所示。因归一化值均小于1,表明与平地相比,边坡的存在确实削弱了 pu值。32°坡角的边坡对 pu值的影响整体上大于20°坡角的边坡。随着距离边坡越近,土层越浅,pu值越小。单桩逐渐远离边坡时,pu值有所增加,且浅层位置增加速度略快。

图12 桩侧土极限抗力比折线Fig.12 Broken lines of ultimate lateral resistance ratio
目前尚没有文献给出砂土边坡条件下桩侧极限抗力的计算公式。本文在试验分析的基础上对现有的砂土平地条件下的桩侧极限抗力公式加以修正,以适应边坡的使用环境。式(4)给出的API 规范up值表达式虽然使用简单,但没有与桩侧极限抗力的产生机制建立联系。Zhang 等[4]在全面回顾前人研究工作[11-12]基础上提出了砂土中桩侧极限抗力的数学表达式为
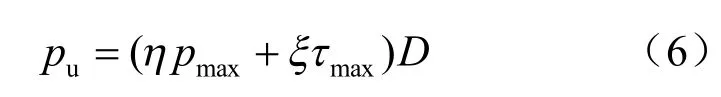
式中:η、ξ为单桩截面的形状系数,圆桩建议取值分别为0.8和1.0。pmax、τmax分别为桩前最大土抗力和桩-土界面最大摩擦力,K γz tan δ,Kp为被动土压力系数,K为与侧向土压力系数K0有关的影响系数,δ为桩-土界面的内摩擦角。将各参数及表达式代入式(6),得到

考虑边坡角度θ和边坡到单桩距离b 对桩侧极限抗力的影响,对桩前最大土抗力 pmax进行修正,引入折减系数 α(α≤1),桩侧极限抗力表达式改为

因桩-土界面摩擦力影响较小,本文不做修正。
对图12 中得到的2 条趋势线进行处理,认为修正系数α与桩坡距离b 近似线性相关:

式中:α1为图12 中归一化曲线的纵坐标截距,与边坡坡角相关。试验结果得到,边坡坡角θ=32°,α1=0.44;θ=20°,α1=0.66;平地时θ=0°,α1=1,发现坡角θ 的正切与α1线性相关,得到
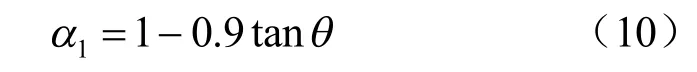
系数α2值基本一致,由最小二乘法拟合,建议α2取值为1/16。经过上述修正,得到考虑边坡影响的浅层土中桩侧水平极限抗力计算公式为
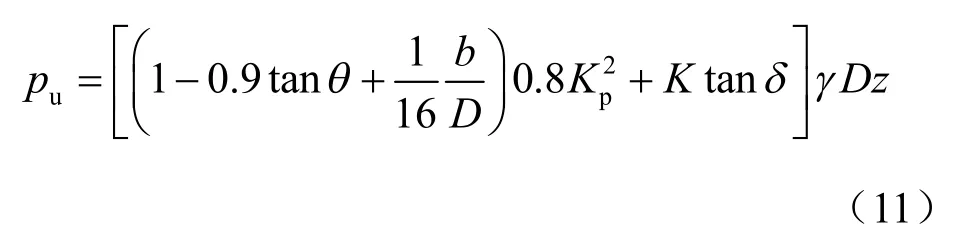
3.5 考虑边坡影响的初始刚度确定
对于双曲线p-y 曲线,控制参数除了桩侧极限抗力 pu外,还有初始刚度 kini。Georgiadis 等[7]根据有限元数值模拟和试验结果,给出了黏土中不排水条件下边坡附近单桩p-y 曲线初始刚度修正公式为
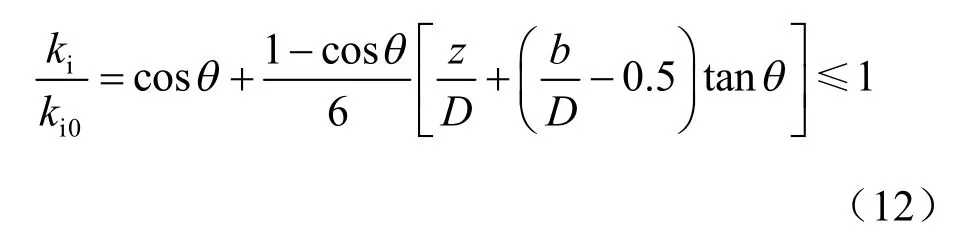
式中:ki0为平地下的p-y 曲线初始刚度;ki为考虑边坡存在时的p-y 曲线初始刚度。
尽管式(12)针对黏土条件,但初始刚度更多的是受土体的弹性力学特性影响,与土的黏聚性关系不大。表6为试验得到的 ki/ki0比值以及由式(11)得到的计算值,对比发现两者误差未超过10%,认为式(11)适用于一般情况。
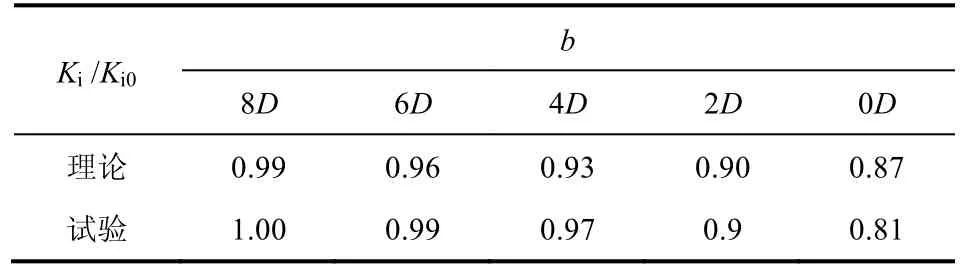
表6 Ki/Ki0理论值与试验值对比Table 6 Comparison between predicted ki/ki0and test data
3.6 计算方法验证
Mezazigh[6]开展了砂土中边坡附近水平受荷单桩的5 组离心模型试验,并对试验p-y 曲线进行了探讨,5 组试验均得到了桩侧极限抗力。本文采用式(12)对这5 组试验数据进行计算,计算值与试验结果的对比如图13 所示,同时也给出了对本文的11 次试验所对应的浅层1D、2D和3D 深度处的桩侧极限土抗力计算结果与试验结果的对比。图中所有散点基本落在等值线周围,吻合程度较好,说明本文给出的计算表达式对边坡附近桩侧极限土抗力的估算有一定的参考价值。

图13 pu值理论和试验结果对比Fig.13 Comparison between predicted pu and test data
图14为Mezazigh[6]离心模型试验p-y 曲线与式(11)、(12)计算得到的双曲线p-y 曲线。
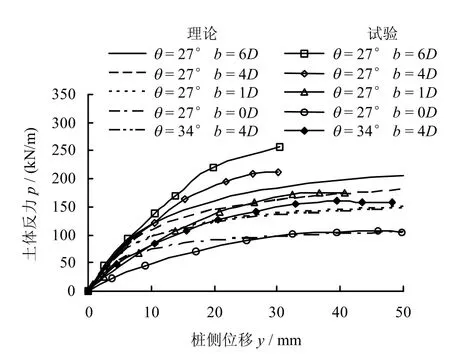
图14 p-y 曲线理论值和离心模型试验结果的对比Fig.14 Comparison between predicted p-y curves and test data
5 组p-y 曲线对应的深度均为1.2 m,边坡坡角θ和单桩到边坡距离b 图中均已标出。由图可见,34°坡角时两者吻合较好;27°坡角时,桩与边坡距离较近的0D 情况两者较吻合。随着距离的增加,1D~3D 的情况在水平位移较大时两者误差增大,且计算值小于试验值。原因可能有以下2 个,对比图13 可知,3 组离心试验 pu值的理论值均略小于试验值;式(12)估算的初始刚度值偏小。但从工程应用角度,本文的计算结果还是可接受的,且偏于保守。
4 结 论
(1)对于水平受荷桩,采用分段3 次多项式拟合桩身应变沿桩身的分布,推导桩侧变形和桩侧土反力是合理的数据处理方法,可以有效地消除数据奇异点。
(2)对于砂土中的水平受荷单桩,API 规范p-y曲线给出的浅层地基初始刚度过大,建议采用双曲线p-y 曲线,由朱斌等给出的表达式计算双曲线的初始刚度。
(3)边坡的存在对单桩的水平抵抗有明显地削弱作用,具体表现为浅层土体抗力减小,桩侧弯矩增大,最大弯矩作用点下移。随着边坡角度增大和桩与边坡距离越近,削弱作用越明显。桩与边坡距离大小有一敏感区,超过该区,边坡影响可忽略。
通过折减系数修正p-y 曲线的桩侧极限抗力和初始刚度来考虑边坡存在对桩基水平抗力的削弱作用,本文提出了砂土中不同边坡角度和桩与边坡距离条件下桩侧双曲线p-y 曲线的计算方法,为边坡附近水平受荷桩的设计提供了依据。
[1]American Petroleum Institute.Recommended practice for planning,designing and constructing fixed offshore platforms[S].USA:American Petroleum Institute,——Working stress design,2000.
[2]KIM B T,KIM N,LEE W J,et al.Experimental Load-transfer curves of laterally loaded piles in Nak-Dong river sand[J].Journal of Geotechnical and Geoenvironmental Engineering,2004,130(4):416-425.
[3]REESE L C,COX W R,KOOP F D.Analysis of laterally loaded piles in sand[C]//Proceedings of 6th Offshore Technology Conference.Houston:[s.n.],1974:473-483.
[4]朱斌,熊根,刘晋超,等.砂土中大直径单桩水平受荷离心模型试验[J].岩土工程学报,2013,35(10):1807-1815.ZHU Bin,XIONG Gen,LIU Jin-chao,et al.Centrifuge modelling of a large-diameter single pile under lateral loads in sand[J].Chinese Journal of Geotechnical Engineering,2013,35(10):1807-1815.
[5]ZHANG L Y,SILVA F,GRISMALA R.Ultimate lateral resistance to piles in cohesionless soils[J].Journal of Geotechnical and Geoenvironmental Engineering,2005,131(1):78-83.
[6]MEZAZIGH S,LEVACHER D.Laterally loaded piles in sand:slope effect on p-y reaction curves[J].Canadian Geotechnical Journal,1998,35(3):433-441.
[7]GEORGIADIS K,GEORGIADIS M.Development of p-y curves for undrained response of piles near slopes[J].Computers and Geotechnics,2012:53-61.
[8]OVESEN N K.The scaling law relationship[C]//Proceedings of the 7th European Conference onMechanics and Foundation Engineering.Brighton:[s.n.],1979:319-323.
[9]陈张林,陈洪,张忠苗.抗水平力单桩p-y 曲线计算公式研究[C]//浙江省第十届土力学及岩土工程学术讨论会,北京:中国建材工业出版社,2004:10-15.
[10]章钊,过超,龚维明.单桩水平承载性能研究[J].路基工程,2010,(5):56-58.ZHANG Zhao,GUO Chao,GONG Wei-ming.Study on horizontal bearing capacity of single pile[J].Subgrade Engineering,2010(5):56-58.
[11]BRIAUD J L,SMITH T O,MEYER B J.Using the pressuremeter curve to design laterally loaded piles[C]//Proceedings of 15th Offshore Technology Conference.Houston:[s.n.],1983:495-502.
[12]SMITH T D.Pile horizontal soil modulus values[J].Journal of Geotechnical Engineering,1987,113(9):1040-1044.
