基于压缩感知的航空货运量模型研究
2014-02-03游庆山徐海文雷开洪
游庆山, 徐海文, 雷开洪, 王 丽
(1. 中国民用航空飞行学院 计算机学院, 四川 广汉 618307; 2. 电子科技大学 电子工程学院, 四川 成都 611731)
航空货运量是反映国民经济发展水平和航空运输经济发展水平的一项重要经济指标,也是航空运输企业进行生产计划与组织需要考虑的重要内容之一.同时,关注航空货运量的未来动态变化趋势,并根据其内在的动态变化趋势采取相应的措施,是航空运输业持续健康发展的有效保障,是航空运输各级决策部门制定发展战略和规划的重要依据[1-2].因此,航空货运量的建模与预测受到国内外学者的广泛关注.
针对航空货运量预测问题,很多学者做了大量而深入的研究.比如,林小平等[3]通过实际数据与预测结果的比较,证明灰色模型对于双流机场货、邮吞吐量的预测具备可行性;文军等[1]研究灰色GM(1,1)理论和回归分析理论在我国航空货运量预测中应用,并建立基于诱导有序几何加权平均(IOWGA)算子的航空货运量组合预测模型,验证结果表明组合预测模型是有效、可靠的,且具有较高的预测精度;周叶等[4]利用我国航空货运量的发展变化具有明显的上升趋势和季节性等特点,建立我国航空货运量的ARIMA模型;方文清等[5]采用基于分形理论的研究方法,从非线性的角度对我国航空货运量进行建模,得到相应的分数维模型.此外,回归分析法、灰色马尔可夫链[2]、分形理论[3]等数学方法同样被用于我国航空货运量的预测问题.
最近十几年,压缩感知(CS)理论[6]得到快速发展,并广泛应用于图像重建、信道估计以及谱估计等不同领域.本文采用压缩感知理论对我国航空货运量进行建模,并以1991~2006年我国航空货运量的统计数据(数据来源于中国统计年鉴)为基础,利用OMP算法得到对航空货运量的压缩感知模型,以期为航空运力市场调控和发展提供理论参考.
1 压缩感知理论
20世纪90年代初,D. L. Donoho等[7]研究小波变换在图像压缩中的应用时,发现用极少数模较大的小波系数就可以获得令人满意的效果.此现象引起了学者对稀疏信号重建的研究.D. L. Donoho等[7]从不同的角度研究信号的稀疏表示,其研究成果指出在一定条件下信号的稀疏表示可以通过非自适应的压缩采样准确重构.从此压缩感知理论,无论是理论研究,还是具体算法设计以及实际应用方面,均得到广泛关注,并在不同应用领域取得满意结果,比如图像处理[8-11]、机器学习[12-13]、波达方向估计[14]、雷达成像[15]、语音处理[16]等.
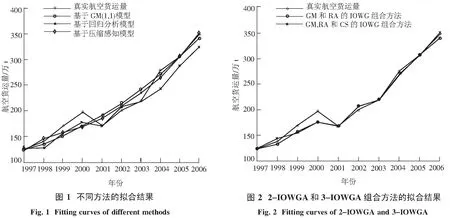
1.1压缩感知模型假设测量向量y∈Rm满足y=Ax+e,求满足测量条件x∈Rn稀疏解的问题即为压缩感知问题,其中,m min‖x‖0 subject to‖y-Ax‖2≤ε, (1) 其中,‖x‖0表示向量x的非零个数. 文献[17]从理论上阐述:如果采用组合优化方法求解(1)式最优化问题,则求解过程是多项式复杂程度非确定性(NP)问题.显然(1)式最优化问题是欠定问题,求解欠定线性方程组传统的算法是以l2范数最小为目标函数.最小范数解可以得到测量向量y在列向量ai中的线性表示,但是最小l2范数解通常不是稀疏解.因此,在求解过程中必须充分利用稀疏性约束.目前求解(1)式最优化问题的常用方法主要分两类:贪婪算法、基于凸优化方法.其中,贪婪算法基本结构是G. Davis等[18]提出的匹配追踪(MP)算法.由于MP算法对信号拟合采用的方法不是正交投影,同时在寻找最优列向量时可能出现重复选择现象,因此,Y. Pati等[19]加以改进,并提出正交匹配追踪(OMP)算法.OMP算法的伪代码如下: Input: 矩阵A∈Rm×n并进行列归一化处理,观测量y∈Rm,误差限制ε,最大迭代次数Kmax. 初始化r0=y,x0=0,Λ0=Ø,l=0. while not converge do compute1:hl=ATrl compute2:Λl+1=Λl∪sup(hard(hl,1)) compute4:rl+1=y-Axl+1 end while 1.2准确重建条件(1)式最优化问题是NP问题,目前所有算法均是近似最优的算法,OMP算法也不例外,因此研究OMP算法准确求解(1)式最优化问题的条件(准确重建条件)成为学术的热点.J. Tropp[20]利用矩阵范数推导了OMP算法的准确重建条件(ERC);M. A. Davenport等[21]利用算子的严格等距性推导了OMP算法的严格等距条件(RIP).这些工作进一步为OMP算法的稀疏重建性能提供了理论上的支持.总之,在一定条件下,OMP算法能准确重建稀疏向量. 为叙述OMP算法的准确重建条件,假设向量y在列向量集ai上的最稀疏表示为: 采用AΛopt表示由指标在集合Λopt中的列向量aλ组成的矩阵,即 AΛopt=[aλ1,aλ2,…,aλm], 其中,λ∈Λopt.采用xΛ表示列由指标在集合Λ中的元素组成的向量,显然有 y=Ax=AΛoptxΛopt. 定理(准确重建条件) 假设向量y能表示成矩阵A中m个列向量的线性叠加,即 y=Ax=AΛoptxΛopt, 如果 (2) 证明假设OMP算法在前k rk=AΛopth. 根据OMP算法的向量选择准则(compute3)可知,要使算法在第(k+1)步准确地选择AΛopt中的列向量,则要满足 拟合残差rk在非最优列向量投影的最大值小于在最优列向量投影的最大值,则有 其中 即任意向量x具有‖Bx‖∞≤‖B‖∞,∞‖x‖∞.利用矩阵范数的性质‖BH‖∞,∞=‖B‖1,1可知 由条件(2)可知结果成立. 下面重点讨论压缩感知理论在我国航空货运量建模中的应用,并通过OMP算法得到航空货运量的压缩感知模型.在压缩感知模型、灰色理论模型以及回归分析模型的基础上进行组合优化,建立了基于诱导有序几何加权平均IOWGA算子的航空货运量组合预测模型. 2.1压缩感知模型文献[1,22]利用回归分析法对航空货运量进行建模,并得到航空货运量的回归分析模型,采用回归分析法分析职工平均工资、人均GDP、GDP和人均消费支出4项指标对航空货运量的影响,得到如下模型 y=195.841-0.043 1x1-0.708 7x2+ 0.054 9x3+0.098 5x4, 其中,y∈Rm表示航空货运量,x1、x2、x3和x4分别表示职工平均工资、人均GDP、GDP和人均消费支出. 上述回归分析存在不足之处,其一,作者仅仅考虑职工平均工资、人均GDP、GDP和人均消费支出4个指标,并没有给出选择指标的理论依据;同时每个指标下均存在许多细化指标,作者并没有考虑细化指标对航空货运量的影响;其二,各指标单位不同,上述回归模型不能直接反映各指标对航空货运量的影响程度. 本文并非简单地扩展指标个数达到精确拟合的效果,而是综合考虑多项指标对航空货运量的影响,并给出选择主要指标的理论依据,得到相对简洁并且拟合精度高的压缩感知模型. 假设极少因素决定我国航空货运量的变化,则航空货运量建模问题可转化为(1)式优化问题.采用OMP算法求解相应问题可得航空货运量的压缩感知模型 y=736.574 3x1+7.713 1x2, (3) 其中,x1表示城镇集体平均工资的归一化向量,x2表示财政支出增长幅度的归一化向量.模型各变量的系数在一定程度上反映该因素影响我国航空货运量的重要程度.模型表明影响我国航空货运量的主要因素是城镇集体平均工资,以及财政支出增长幅度. 利用(3)式航空货运量的压缩感知模型可以预测2007年我国的航空货运量.预测值为416.57万t,2007年真实的航空货运量为401.8万t,预测误差为3.67%.预测的结果表明压缩感知模型可应用于短期内我国航空货运量的预测,可以为进一步的航空货运市场调控提供有效理论依据. 2.2IOWGA算子的组合优化模型在航空货运量预测问题中,假设x1t、x2t、x3t分别表示3种不同方法在t时刻的拟合值,l1、l2、l3分别为诱导有序几何加权平均的权系数,Pit表示第i拟合方法在t时刻的拟合精度,其定义如下 显然Pit∈[0,1]. 将第t时刻预测精度与其对应的预测值关联可得3个二维数组〈P1t,x1t〉、〈P2t,x2t〉、〈P3t,x3t〉,其中,t=1997,…,2006.假设L=(l1,l2,l3)表示权系数向量,并对预测精度Pit按从大到小排列,设Pindex(ix)表示第i个较大预测精度的下标,则有 IOWGAL(〈P1t,x1t〉,〈P2t,x2t〉,〈P3t,x3t〉)= 称上式为由预测精度序列Pit所产生的t时刻的IOWGA组合预测值[1,23].显然n期组合预测对数总误差平方和S为 其中 eaindex(it)=lnxt-lnxPindex(ix). 用Eij简记 则可得三阶组合预测对数误差信息矩阵E=(Eij). 使n期组合预测对数总误差平方和S最小可以得到组合预测权系数l1、l2、l3,即L可以通过如下非线性规划模型求得 minS(L)=LTEL, (4) 将航空货运量的灰色理论模型、回归分析模型以及基于压缩感知模型进行诱导有序几何加权平均可得IOWGA组合模型. 假设x1t、x2t、x3t分别为灰色理论拟合值、回归分析拟合值以及基于压缩感知的拟合值,l1、l2、l3表示组合拟合中的权系数.将拟合值代入(4)式模型,可以得到优化问题 采用压缩感知理论得到的预测模型具有如下优点:第一,模型非常简洁;第二,模型中各分量的系数可以体现各分量在航空货运量中的比重;第三,从模型比较可知,基于压缩感知的模型具有更高的精度. 文献[1]提出基于灰色理论的航空货运量预测模型,同时进一步给出基于回归分析、灰色理论的我国航空货运量IOWGA组合拟合值(简记为2-IOWGA),其中,基于灰色理论预测模型如下 下面将详细比较压缩感知模型、灰色理论模型、回归模型对我国航空货运量的拟合效果,并进一步比较2-IOWGA、3-IOWGA对我国航空货运量的拟合效果. 拟合图1给出航空货运量的真实值以及基于压缩感知模型、灰色理论模型、回归模型等不同方法所得拟合结果.图1结果表明,基于压缩感知模型是可靠的,并具有较高的拟合精度,可应用于实际预测.图2结果表明,3-IOWGA相对于2-IOWGA具有较高的拟合精度. 按照拟合效果评价原则和惯例,采用5项拟合误差指标[22,24](平方和误差(SSE)、均方误差(MSE)、平均绝对误差(MAEstro)、平均绝对百分比误差(MAPE)和均方百分比误差(MSPE))作为评判准则,对基于压缩感知模型、灰色理论模型、回归模型、2-IOWGA组合模型、3-IOWGA组合模型进行评价.各方法的拟合误差指标如表1所示. 对预测效果进行综合性评价,通过不同拟合模型的拟合值比较(图1和图2所示)和各拟合模型的拟合误差指标(表1所示),可以得到:单种拟合方法中,基于压缩感知的拟合模型相对于灰色理论、回归分析方法的拟合模型具有模型相对简洁、拟合精度高、误差小等特点.拟合误差指标结果表明,基于压缩感知方法的拟合精度高于灰色理论与回归分析方法,同时3-IOWGA组合模型拟合精度高于2-IOWGA组合模型拟合精度. 表 1 拟合误差指标 本文将压缩感知理论引入航空货运量预测领域,通过OMP算法得到基于压缩感知理论的航空货运量预测模型,并给出基于压缩感知模型的2007年预测值.预测结果表明,压缩感知模型可应用于短期内我国航空货运量的预测.本文重点比较压缩感知模型、灰色理论模型、回归分析模型在航空货运量的拟合效果.通过对预测误差以及拟合误差指标的比较,得到压缩感知模型具有模型相对简洁、精度高、误差小等优点.同时给出基于压缩感知模型、灰色理论模型、回归模型3种方法的IOWGA组合优化模型,实验表明,3-IOWGA组合模型相对于2-IOWGA具有更好的统计特性. [1] 文军,蒋由辉,方文清. 航空货运量的优化组合预测模型[J]. 计算机工程与应用,2010,46(15):215-217. [2] 文军. 基于灰色马尔可夫链模型的航空货运量预测研究[J]. 武汉理工大学学报:交通科学与工程版,2010,34(4):695-698. [3] 林小平,袁捷. 基于灰色模型的成都双流机场物流预测[J]. 武汉理工大学学报:交通科学与工程版,2007,31(3):457-459. [4] 周叶,肖灵机. 基于ARIMA 模型的我国航空货运量预测分析[J]. 南昌航空大学学报:社会科学版,2010,12(3):22-27. [5] 方文清,蒋由辉,文军. 分形理论用于航空货运量的预测[J]. 交通科技与经济,2009,11(2):105-106. [6] You Q S, Wan Q, Liu Y P. A short note on strongly convex programming for exact matrix completion and robust principal component analysis[J]. Inverse Problems and Imaging,2012,6(2):357-372. [7] Donoho D L, Johnstone I. Wavelet Shrink-age: Asymptopia[R]. Stanford:Stanford University,1993. [8] Ellenberg J. Fill in the blanks: using math to turn lores datasets into hiressamples[J/OL]. Wired Magazine,2010,18(3). http://www.docin.com/p-62893506.html. [9] 王良君,石光明,李甫,等. 多稀疏空间下的压缩感知图像重构[J]. 西安电子科技大学学报:自然科学版,2013,40(3):88-98. [10] Duarte M, Davenport M, Takhar D, et al. Single-pixel Imaging via compressive sampling[J]. IEEE Signal Processing Magazine,2008,25(2):83-91. [11] Shi G M, Gao D H, Song X X, et al. High-resolution imaging via moving random exposure and its simulation[J]. IEEE Transactions on Image Processing,2011,20(1):276-282. [12] Zeng B, Fu J. Directional discrete cosine transforms: a new framework for image coding[J]. IEEE Trans Circuits Syst Video Technol,2011,18(13):305-313. [13] Ji H, Liu C Q, Shen Z W, et al. Robust video denoising using low rank matrix completion[J]. Comput Vision and Pattern Recognition,2010:1791-1798. [14] Malioutov D, Cetin M, Willsky A S. A sparse signal reconstruction perspective for source location with sensor arrays[J]. IEEE Transaction on Signal Processing,2005,53(8):3010-3022. [15] Matthew H, Thomas S. Compressed sensing radar[J]. IEEE International Conference on Acous-tics, Speech and Signal Processing,2008:1509-1512. [16] 梁瑞宇,邹采荣,赵力,等. 语音压缩感知及其重构算法[J]. 东南大学学报:自然科学版,2011,41(1):1-5. [17] Natarajan B K. Sparse approximate solutions to linear systems[J]. SIAM J Comput,1995,24(2):227-234. [18] Davis G, Mallat S, Zhang Z. Adaptive time-frequency decompositions[J]. SPIE J Opt Eng,1994,33(7):2183-2191. [19] Pati Y, Rezaifar R, Krishnaprasad P. Orthogonal matching pursuit: recursive function approximation with applications to wavelet decomposition[C]//The 27th Annual Asilomar Conference on Signals, Systems, and Computers. Pacific Grove,CA,1993. [20] Tropp J. Greed is good: algorithmic results for sparse approximation[J]. IEEE Trans Inform Theory,2004,50(10):2231-2242. [21] Davenport M A, Wakin M B. Analysis of orthogonal matching pursuit using the restricted isometry property[J]. IEEE Trans Inform Theory,2010,56(9):4395-4401. [22] 方文清. 我国航空货运业发展若干问题研究[D]. 广汉:中国民航飞行学院,2009. [23] Chou K C, Zhang C T. Predicting protein folding types by distance functions that make allowances for amino acid interactions[J]. J Biol Chem,1994,269:22014-22020. [24] 王洋. 组合预测模型在成都市房价中的应用研究[D]. 成都:成都理工大学,2010.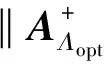
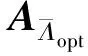
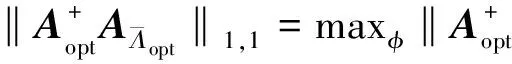
2 航空货运量的压缩感知模型
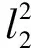
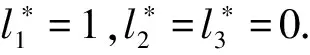
3 模型分析与比较

4 结语
