一种新的遥感影像角点提取方法

宋妍，苟永刚，郑坤

(中国地质大学 信息工程学院，武汉 430074)

1 引 言

角点是影像重要的局部特征，直观定义为至少在两个方向上影像的灰度值变化较大的点。实际影像中，(地物)轮廓的拐点、线段的末端都可认为是角点。角点在各种影像特征中具有关于灰度变换和旋转均保持不变的特点。角点的提取可以减少参与计算的数据量，同时又不会造成影像信息量的损失，利用角点的匹配可以大大提高匹配效率，因此，角点在影像匹配、目标识别、影像融合和超分辨率重建等方面有着广泛的应用。如何快速准确的提取影像中的角点成为一个关键问题。目前角点提取方法主要分为基于影像边缘的方法和基于影像灰度的方法[1]。基于边缘的方法首先需要对影像进行分割和边缘提取，提取角点的准确性很大程度上取决于影像分割和边缘提取的精度。基于影像灰度的方法主要考虑像素点邻域内灰度变化，通过计算点的曲率和梯度来提取角点，目前这种方法应用较广泛。

1998年，M.Trajkovic 和 M.Hedley提出了一种基于影像灰度的简单快速的角点提取方法，即MIC(Minimum Intensity Change)算法[2]，它因方法简单、处理速度快等特点而受到重视，然而MIC算子对边缘和拐角处的噪声较敏感，尤其对斜线状的边缘反应剧烈，会提取出较多的伪角点，影响其提取效率，从而在实际应用中并没得到广泛使用。本文首先介绍了MIC算子的原理及其存在的主要问题，而后针对该问题提出了EMIC(Enhanced MIC，增强型MIC)算子，以解决其在抗噪性方面的问题。最后进行了试验，首先将EMIC算子与MIC算子的性能进行比较，然后将EMIC算子与经典的点特征算子(Moravec[3]，Forstner[6]，Susan[4]等)进行比较。实验结果表明：EMIC算子具有更快的角点提取速度，抗噪性更强，有更好的实用性。

2 EMIC算子原理

2.1 MIC算子原理及存在问题

MIC算子考虑在一个小圆形窗口中，在通过圆心的所有直线方向上的灰度变化。如图1所示，若假设任意的一条通过圆心C的直线与圆的边缘分别交于点p和p′，则MIC算子的角点响应函数定义为：

(1)

图2显示了MIC算子在不同情况下的反应，图2(a)中圆形窗口的大部或全部在黑色矩形区域内部，则在若干条直线上满足Ip≈Ic≈Ip′；图2(b)中圆形窗口的圆心C在矩形区域边缘上，则存在一条直线使得Ip≈Ic≈Ip′；图2(c)中圆形窗口处于角点位置，在任意一条直线上的Ip和Ip′均与Ic不同；图2(d)中圆形窗口的圆心C处于一个孤立像素点上，在任意一条直线上的Ip和Ip′均与Ic不同。

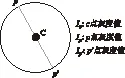
图1 MIC算子模板

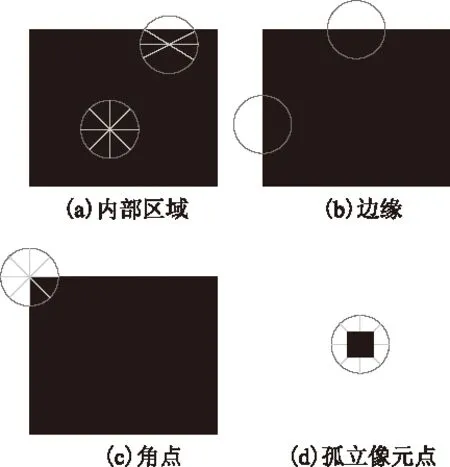
图2 MIC算子的不同情形

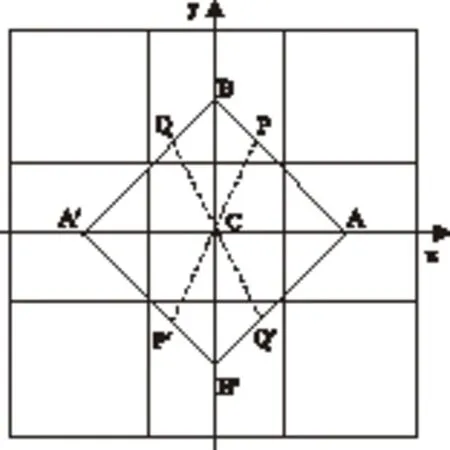
图3 3*3窗口内插估计

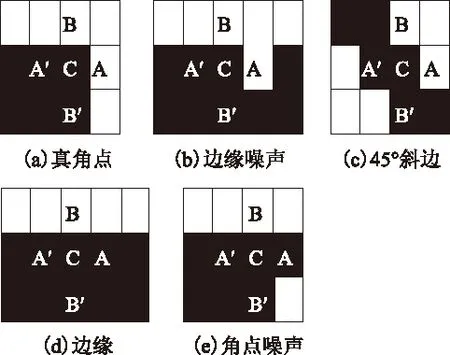
图4 MIC算子对噪声敏感

实际应用中，MIC算子提取角点分为两步，如图3所示，首先根据式(1)分别计算垂直方向点B和B′、水平方向点A和A′相对于点C的灰度变化最小值，然后计算内插点Q和Q′、P和P′相对于点C的灰度变化最小值，最后将最小值与经验阈值比较，以确定是否为角点。

MIC算子虽是一种简单、快速的角点提取算子，但MIC算子对噪声敏感，尤其在斜线方向会提取出较多的伪角点。如图4所示，MIC算子可能将一个边缘噪声点确定为一个角点，同样的，也可能将一个真实角点误判为边缘点。图4(c)说明MIC算子对斜线边缘敏感的原因，45°边缘拥有和真实角点相同的性质，容易想象，其他类型的有一定角度的边缘也具有该性质，如此在斜线边缘上便会提取出大量的伪角点。

2.2 EMIC算子设计与方法

为了从斜线边缘中区分出真正的角点，这里将MIC做了改进，提出一种抗噪性较强的EMIC算子，算子模板如图5所示，EMIC算子将MIC算子的4邻域模板扩展至8邻域、16邻域或者更多，EMIC算子除了计算MIC算子中水平、垂直和对角方向的灰度值变化外，还从其他的8个区域来对角点进行约束。对于真角点(图4(a))和边缘(图4(d))，EMIC算子保留了MIC算子的识别能力；而对于边缘噪声(图4(b))、45°斜边(图4(c))和角点噪声(图4(e))，由于EMIC算子考虑的邻域范围较广，有效地消除了此类噪声。

EMIC算子将一个以像素点C为中心的窗口以直线(数字标记)通过区域Edge1、Edge2、…、Edge8为边界划分为8个区域TIN1、TIN2、…、TIN8，将每个区域(包括边界区域)作为一个整体看作是一个像素点P，并将该区域灰度均值作为P点灰度值IP，记p′为p关于点C的对称点，则利用公式(1)计算在pp′方向上的灰度变化值。

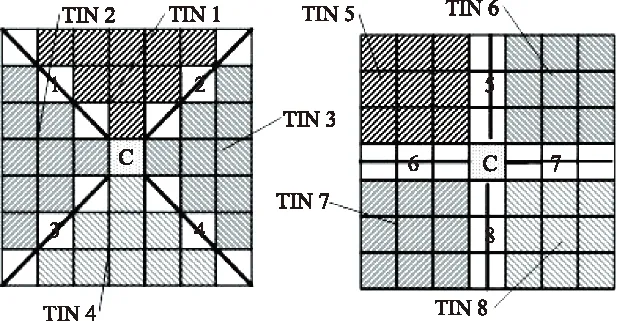
图5 EMIC算子模板

EMIC算子定义边界区域角点响应函数为：

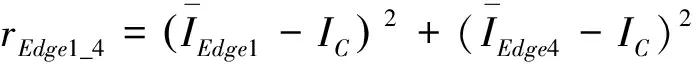
(2)

EMIC算子定义TIN区域角点响应函数为：

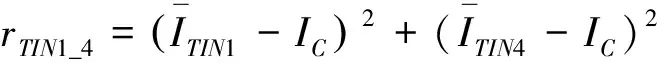
(3)

其中，

均表示其对应区域灰度均值。

3 试验及讨论

从兴趣算子的定位精度、抗噪性(尤其是斜线边缘的抗噪性)和适应性方面对其进行评估，其中适应性比较借鉴文献[5]提出的重复率标准。重复率定义为两幅影像中重复点的数量和检测出的总点数之比，由于两幅影像中提取出的特征点数不一定相等，仅有较少的角点可以被重复，因此重复率的定义由式(4)给出：

(4)

其中，Nrepeat是两幅影像中重复点数，N1，N2分别为两幅影像中提取的特征点。

3.1 EMIC算子与MIC算子性能比较试验

图6显示了MIC算子和EMIC算子分别应用于人造测试图像的角点检测结果。沿着45°角的边缘，EMIC算子检测出的错误角点少于MIC算子检测出的错误角点，并且EMIC算子对角点有较好的定位精度。但人工测试影像清晰的表明EMIC算子依然对某些斜线边缘有较强烈的反应。

图6 MIC算子和EMIC算子应用于人工图像

图7显示了MIC算子和EMIC算子分别应用于块状测试图像的角点检测结果。两个算子均选择最优参数，以保证获取最大的角点量的同时得到的伪角点量也最小。从检测结果可以看出，EMIC算子较MIC算子有了很大的改进，但是沿着某些斜线边缘，EMIC算子仍然会检测出一些错误角点。

图7 MIC算子和EMIC算子应用于块状图像

EMIC算子有好的定位精度和高效的运算效率，较MIC算子有了很大的提高。但是，以上测试影像也清楚说明，由于EMIC算子对某些斜线方向的边缘敏感，会在斜线方向边缘处检测出较多的伪角点，导致EMIC算子的检测效率较低。

3.2 EMIC算子与经典点特征提取算子比较试验

重复率可以在一定程度上衡量角点提取算子在几何畸变、辐射畸变等影响下的独特性、不变形和稳定性。重复率越高，角点算子稳定性越好，可能匹配的点就越多。这里选用了同一地区不同时相的两幅变形较大的遥感影像(在x，y方向均有位移)，实验过程中采用先人工选取3对控制点，再分别利用Moravec算子，Forstner算子，Susan算子，MIC算子和EMIC算子自动提取角点，然后利用相关系数法完成两幅影像同名角点的匹配，最后对各算子的重复率进行比较。实验影像如图8所示，两幅影像的大小均为400*400。

计算重复率时，为保证匹配的可靠性，匹配可靠度ψ的阈值选取较大的值，其取值范围为ψ∈0.70,0.95，重复率比较结果如图9所示。

图9显示，随着匹配可靠度ψ值从0.7到0.95的增加，各算子重复率也随之下降，这是由于随着匹配可靠度的增加，符合要求的匹配点对数量会随之减少的缘故。此外，本实验中各算子重复率都较低(均小于10%)，可能是由于遥感影像的特殊性且其形变较大，各算子提取的特征点数较多，但匹配的点对却较少的缘故，但各算子的重复率仍然具有可比性。

图8 实验影像对

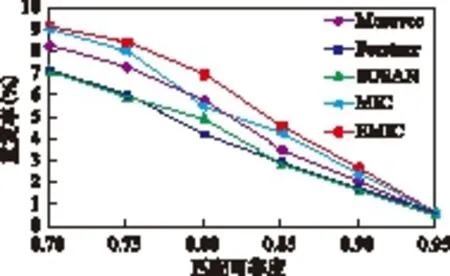
图9 重复率比较

从图9也可看出，EMIC算子的重复率总体上要优于其他算子，由于EMIC算子对线的拐点、边缘较为敏感，所提取的特征点均为物体的拐点(如房屋轮廓的拐点、道路交叉点等)，而在此处纹理变化都比较剧烈，所以对于受到几何畸变、辐射畸变影像的两幅影像而言，在纹理变化剧烈区域较易识别同名点。而对于其他算子，其可能在物体内部确定特征点(如房屋轮廓内灰度变化较剧烈的屋顶等)，而对于不同时相的两幅遥感影像中的同名位置，其局部灰度的相关性可能并不高。此外，对于不同时相的遥感影像，其他各算子提取出了很多特征并不明显(兴趣值不大)的点，这些特征并不明显点增加了后续匹配过程中发生误匹配的几率，同时降低了重复率。

4 结束语

EMIC算子角点提取速度快，且对角点特征较规则的影像有较好的识别能力，所以对于重视运算效率的实时应用，或者是对于角点特征较为规则的影像，EMIC算子具有明显的优势，可以考虑使用EMIC算子进行角点检测。然而，MIC算子和EMIC算子都不具有旋转不变性，且它们都对某些斜线边缘敏感，尽管EMIC算子重复率较高，但它会在斜线边缘提取出较多的伪角点，在匹配的过程中会有一些伪角点参与匹配，导致匹配的同名点对中会有一些伪角点的匹配点对。如何进一步提高EMIC算子对斜线边缘的抗噪能力，将会是下一步的研究重点。

[1] 张春美,龚志辉,黄艳.几种特征点提取算子的性能评估及改进[J].测绘科学技术学报,2008,25(3):231-234.

[3] HANS P M.Towards automatic visual obstacle avoidance[C]//Proceedings of the 5th International Joint Conference on Artificial Intelligence.1977: 584-584.

[4] SMITH S M,BRADY J M.SUSAN—A new approach to low level image processing[J].International Journal of Computer Vision,1997,23(1): 45-78.

[5] SCHMID C,MOHR R,BAUCKHAGE C.Evaluation of interest point detectors[J].International Journal of Computer Vision,2000,37(2): 151-172.

[6] FÖRSTNER W,GüLCH E.A fast operator for detection and precise location of distinct points,corners and centres of circular features[C]//Proc.ISPRS Intercommission Conference on Fast Processing of Photogrammetric Data.1987: 281-305.

[7] PARKS D,GRAVEL J P.Trajkovic Operator[EB/OL].http://kiwi.cs.dal.ca/～dparks/CornerDetection/trajkovic.html.