基于小波NEIGHSHRINK阈值法滤除SAR斑点噪声

宁凯，李爱农，陈强，靳华安

(1.中国科学院水利部成都山地灾害与环境研究所，成都 610041；2.西南交通大学遥感信息工程系，成都 610031)

1 引 言

合成孔径雷达(SAR)成像系统实现了同时对地物目标的距离向和方位向的高分率成像，且其不受天气影响，能够进行全天时、全天候的对地观测，在农业、林业、军事等领域都展现出了巨大的应用潜力。然而，包括SAR系统在内的所有基于相干成像机制的系统都无可避免地会产生影像斑点噪声[1]。完全发育的斑点噪声在影像中呈现杂乱无序的状态[2]，不仅影响影像的视觉效果，而且在一定程度上降低了影像质量，严重干扰了影像解译、地物目标信息提取、分类、参数反演等后续应用。

当前，基于真实影像特征和噪声分布特性的分析，已经提出了大量的图像噪声抑制算法，这些方法按其作用域的不同可分为空间域和变换域两大类。其中，空间域算法是直接作用于原影像，对灰度值作相关处理，代表性方法有均值滤波、中值滤波等[3]。而变换域算法一般需分三个步骤完成：(1)变换处理，把原影像从空间域变换至频率域或小波域；(2)对变换后系数作相应运算处理，以滤除噪声；(3)逆变换处理，重构去噪后影像，例如傅里叶滤波、小波滤波等[4]。空间域算法出现时间要相对较早且已具备比较完备的理论基础，属于经典的去噪算法，而变换域滤波可以说是一种“年轻”的算法，其中的小波去噪算法是自20世纪90年代才开始出现在有关信号和图像处理研究的文献中[5]。该算法是基于小波变换原理，在小波域对小波系数作非线性处理，达到滤除噪声的目的。近年来小波理论的研究受到持续关注，基于小波分析的滤波思想也渗透到了许多理论和应用领域。Donoho和他的研究团队率先提出了小波域阈值滤波算法，通过设定一适当阈值，认为小于该阈值的系数由噪声产生，直接置零；大于阈值的系数，利用硬阈值函数或软阈值函数将其保留或做收缩运算，从而抑制信号中的噪声[5]。该算法在诸多应用实例中都取得了不错的效果，但同时也正如Coifman和Donoho所指出的，采用该算法滤波后的影像在视觉效果上出现了邻近Gibbs现象的不连续性[6]。为此研究者们在该算法的基础上进行了一些改进。考虑到经小波变换后得到的小波系数相互之间具有相关性，即在一个大的小波系数周围往往分布的也是数值较大的小波系数，Cai和Silverman[7]提出小波域NEIGHCOEFF算法用于一维信号的去噪处理。他们指出，试验结果表明改进算法的滤波效果明显优于传统的逐系数去噪法。Chen和Bui[6]把NEIGHCOEFF思想延伸应用到了二维图像的处理当中，并通过仿真实验验证了它滤波效果的优越性。

尽管小波滤波理论和相关技术研究已经取得较大进展，但在工程应用领域的发展相对滞后，大部分的应用研究还主要局限在仿真实验阶段。本文将小波域NEIGHSHRINK阈值算法应用于实际的SAR影像的滤波处理中，以ALOS PALSAR为试验数据源，从SAR影像斑点噪声的数学统计特征出发，详细阐述了小波域NEIGHSHRINK阈值算法的实现过程。试验还同时实现了LEE、增强型LEE和基于最大后验概率的GAMMA等三种常用的算法。结合目视判读和比值图像、等效视数、归一化均值等评价指标从定性和定量两方面开展对各滤波器试验结果的比较分析。最后对小波域阈值算法应用于实际SAR影像的滤波处理进行了讨论和展望。

2 小波NEIGHSHRINK阈值算法与实现

2.1 斑点噪声的数学统计特征

从SAR成像机理出发，理论上假设每个分辨单元内包含着大量的等强度散射子，根据中心极限定理，I、Q通道数据是服从零均值高斯分布的，因此可以推导得出强度I(x,y)服从负指数分布。但事实上，由于SAR原始粗数据加工处理的复杂性使得在实际应用中很难得到一个信噪模型[8]。通过对SAR斑点噪声统计特性的分析，Goodman提出完全发育的斑点噪声的概念，证明斑点噪声在满足完全发育的条件下可模型化为一种乘性噪声[9]，即：

Ix,y=Rx,y·Nx,y

(1)

其中，Ix,y表示观察到的图像强度，Rx,y代表希望恢复的未被噪声污染的真实图像强度，Nx,y则是同真实图像相互独立，均值为1，标准差为σN的乘性噪声。这个模型也成为了后来SAR的研究基础。

在假定乘性模型的前提下，对(1)式作对数运算得到如下表达式：

ln(Ix,y)=ln(Rx,y)+ln(Nx,y)

(2)

为简化分析，一些研究者认为噪声分量在对数强度域是服从零均值高斯分布的[10]。

2.2 小波变换数学原理

小波变换是20世纪80年代中后期逐渐发展起来的一种新的数学工具，它的出现弥补了傅里叶变换不能描述随时间变化的频率特性的不足，也诞生了一种新的滤波思路[4]。众所周知，设ψ(t)∈L2(R),若ψ(t)满足如下的允许性条件：

(3)

则称函数ψ(t)为一个基本小波或母小波。对母函数ψ(t)进行伸缩和平移操作得：

(4)

函数族{ψa,b(t)}称为小波或小波基，其中a表示尺度因子，b表示平移因子[11，12]。当参数a,b取区间范围内的连续变量时，信号函数f∈L2(R)则可用函数Uf来表示：

(5)

映射函数U被称作“连续小波变换”。若将a按幂级数离散，b在尺度内均匀离散，即a=a0m，b=nb0a0m且满足a0>1,b0≠0的条件，那么小波基ψa,b(t)变作：

ψa,b(t)=|α|-m/2ψ(a0-mt-nb0)m,n∈Z

(6)

信号函数f∈l2(Z2)的离散小波变换为[5，13-14]：

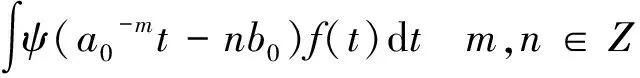
(7)

(3)式是小波函数需满足的基本条件，根据所选母函数ψ(t)的不同，可构成多种形式的小波基。不同的小波基对信号的描述不同，对信号作小波变换时，都希望选择的小波基能同时具备以下性质：①对称或反对称；②正则性;③较短的紧支集；④正交性；⑤较高的消失矩[5]。对称性和正则性反映的是小波基的重构性能，目前常用的小波基均已具有良好的正则性和对称性。紧支性反映了小波基的局部化能力，越短的紧支集表示小波基越好的局部化特性和小波变换越低的计算复杂度。而正交性则反映出经小波变换得到的各个频段上系数的相关性，具有正交性的小波基，相关性较小，有利于影像的重构和数值计算。消失矩的大小决定了用小波逼近光滑函数的收敛率，而高的消失矩利于抑制SAR影像的斑点噪声[15]。但是要使一个小波基同时满足上述条件是不现实的，Daubechies已证明，除Haar小波基外，不存在对称的紧支正交小波基，因此在实际应用中应根据具体需要综合考虑小波基的数学特性来选择合适的小波基。

2.3 小波NEIGHSHRINK阈值算法

基于小波分析的图像滤波算法，包括三个基本步骤，首先要做的是把图像由空间域变换至小波域。由于图像是二维信号，所以需要将一维小波变换扩展到二维空间。令f(x,y)∈L2表示一个二维信号，x,y分别表示其横坐标和纵坐标。图像的二维离散小波变换是用低通滤波器和高通滤波器分别沿f(x,y)的x方向和y方向作分解，如图1的(a)，(b)两图所示。一幅图像经一级分解后变作四小幅，其中左上角LL为平滑逼近，其余三幅为细节图像，分别是垂直分量LH，水平分量HL和对角分量HH[16-17]。下一级的分解只在上一级产生的低频子带LL上进行，同样产生四个子带，如(c)图所示。这样的分解过程持续至预先设定的分解层数止。

图1 二维图像的小波分解

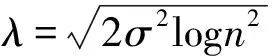
(8)

βx,y=(1-λ2/S2...βx,y)+

(9)

dx,y=dx,y×βx,y

(10)

这里的S2为移动窗口内小波系数dx,y的平方和，βx,y为收缩因子。(9)方程式末尾的“+”号表示若计算得到的βx,y为负值，则设为0，反之则保持为原计算值。

其中，计算通用阈值时用到的σ为原图像的噪声标准差，估计噪声标准差的方法有很多，最常用的是最高频子带绝对值中值法，但是由该方法得到的估计值往往比实际小，不适用于斑点噪声比较严重的SAR影像。因此，本文采用由Guo等人改进的估算方法。若假设d1x,y是小波域第一层分解中最高频子带HH1的系数，那么：σ=median(|d1x,y|)/0.675[2]。

由上述小波变换数学原理的内容可知，小波基的选择主要依据小波基本身的数学特性。根据小波基选择的一般原则，并结合影像处理的预期目标，本次试验选用4阶Daubechies小波基。Daubechies小波系是由法国著名小波分析学者Ingrid Daubechies于上世纪90年代初提出并构造的一系列二进制小波的总称，简写为dbN，N是小波的阶数。dbN小波与经典小波不同，它不能由一个简洁的表达式ψ(t)给出，而是通过一个称作“尺度函数”的φ(t)加权组合产生。dbN小波是正交小波，也是双正交小波，并且是紧支撑的，同时具有在时域ψ(t)有N阶消失矩，在频域Ψ(ω)的ω=0处有N阶零点的特征。该小波对应的滤波器组属共轭正交镜像滤波器组，Daubechies提出的dbN小波的构造方法即是从该滤波器组出发，通过设计得到符合要求的共轭正交滤波器，然后由其构造出尺度函数和小波函数[18]。

另外，移动滤波窗口大小的选取对滤波效果也有着不可忽略的影响。通过试验比较发现，随着窗口的增大，影像的过平滑现象愈严重，因此，一般选用中间大小的3×3或5×5窗口。

利用小波滤波算法对SAR影像作小波变换前，先要对SAR影像作对数运算，变乘性噪声为加性噪声。本文利用小波NEIGHSHRINK阈值算法滤除SAR影像斑点噪声的实现流程如图2表示。

图2 小波NEIGHSHRINK阈值算法滤除SAR斑点噪声流程图

3 作为对照的三种空间域算法

(1)LEE算法

在缺乏信号精确模型的情况下，Lee提出使用5×5或7×7大小的窗口统计影像本身局部样本的均值和方差作为先验均值和方差[8]，该算法是利用图像局部统计特性进行SAR图像斑点滤波的典型代表之一[1]。基于完全发育的乘性噪声模型，由最小均方根误差准则推导得到LEE滤波器。

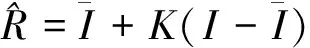
(11)

(12)

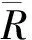
(13)

(14)

(2) GAMMA_MAP算法

最大后验概率(MAP)的滤波算法是把图像的平面坐标加上强度值考虑为三维模型，是一种典型的几何滤波器[1]。Kuan等人[19]率先提出MAP滤波的基本思想，该算法的核心是基于后验概率最大化时对真实图像的估计。假定真实图像和噪声都服从Gamma分布，则可得到如下MAP滤波方程：

(15)

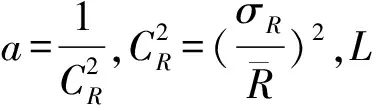
(3)增强型LEE算法

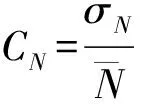
(16)

4 试验与结果分析

4.1 试验数据

采用的SAR影像由日本ALOS卫星携带的相控阵型L波段合成孔径雷达(Phased Array type L-band Synthetic Aperture Radar，PALSAR)传感器获取。PALSAR是一台主动式微波传感器，波长为0.236m(L波段)，具有高分辨率、扫描式合成孔径雷达、极化三种观测模式，能获取比普通SAR更宽的地面幅宽。

实验数据为一幅高分辨率观测模式的升轨右侧视影像，覆盖区在中国岷江上游地区，幅宽为70km×70km，入射角为38.635°，四个角点的地理坐标分别为：103.573286°E，30.937031°N(左上)，104.496497°E,30.937031°N(右上)，103.573286°E，31.953382°N(左下)，104.496497°E，31.953382°N(右下)，且于2010年10月27日15点33分13.095999秒成像。本文裁剪原始影像中512×512面积的区域(如图3所示)作为实验区。该实验数据经过前期的聚焦和多视处理，方位向分辨率为12.575m，距离向分辨率为15.005m。由图3可以看出，实验区属于典型的高山峡谷地区。

图3 (a)含噪原始SAR图像,(b)对应区SPOT影像((a),(b)两图中红色曲线部分表示图中主要的山脊线和山谷线走向，红色圆形区对应着两个湖泊)

众所周知，SAR系统由于其侧视成像特点，原始影像几何失真大，而在坡度起伏变化大的山区地段失真现象更为严重。如透视收缩(foreshortening)现象：面向雷达方向的坡面在SAR斜距影像上被缩小，使得一定面积上的能量在成像过程中被压缩至相对较小的坡面上，因而在影像上面向雷达照射方向的坡面看上去要比周围区域亮许多(如图3(a)图的3号框区域所在的坡面即产生了透视收缩现象)。透视收缩的比率与坡度及局部入射角有关，其极端情况即产生叠掩现象。叠掩现象是雷达俯角与坡度角之和大于90°，换句话说就是地物目标到SAR方向的局部入射角为负时，从坡面的顶部反射的信号要先于坡面底部反射信号到达传感器，从而在SAR影像上呈现为坡的顶、底颠倒的情况；而若坡面背向雷达照射方向且背坡坡度大于雷达俯角，则会因为雷达信号的无法到达使其成为雷达图像中的阴影区(如图3(a)图左上角的1号框区域)。

4.2 算法实现

为便于比较评价小波NEIGHSHRINK阈值算法的滤波效果，本文统一采用5×5大小的移动滤波窗口(如图4所示)，借助ENVI+IDL编程语言，利用算法程序同时实现了小波NEIGHSHRINK阈值算法、LEE滤波、增强型LEE滤波和基于最大后验概率的GAMMA滤波算法。

图4 5×5移动滤波窗口

4.3去噪效果评价

一个有效的SAR影像降噪算法应该具备如下特性：①有效的抑制斑点噪声；②尽量的恢复原信号，保持原图像的纹理结构。一般对试验结果的比较评价从目视判读和定量指标两方面开展，需要从影像的平均值保持、方差的减少、人眼视觉效果等几方面考虑[22-23]，常见的定量指标有均值，方差，比值图像，等效视数，均值归一化指数等。其中等效视数(ENL)作为一个衡量相干斑强度极好的测量度[24]，常被用来评价滤波器的噪声抑制能力，其数学表达式如(17)式所示。对于同一幅影像，滤波算法的等效视数ENL值越大，则表示该方法的斑点噪声滤除能力越强。而一种“理想”的滤波器还应该做到在有效去除斑点噪声的同时尽量恢复原信号[20]。简单来说，就是要求滤波器除了能够有效抑制噪声外还能很好地保持一幅SAR影像总体的辐射特性和纹理结构信息，这可从比值图像、归一化均值(NM)等方面进行评价[24]。在(1)式的假定前提下，原始影像同滤波后影像的比值，即为灰度均匀，没有任何纹理结构信息的噪声图像，该比值图可被用来评价总体的辐射特征和结构信息的保持[9]。均匀区域图像的均值反映出辐射特性的保持能力，通常以滤波后图像与滤波前图像均值之比作为归一化均值保持指数，可由如下(18)式计算得到。

(17)

(18)

4.4 结果与分析

原始含噪图像经不同滤波器滤波后的效果图分别如图5所示。从视觉效果角度看，四种滤波器都能比较有效地抑制斑点噪声，增强影像的可读性。但是，首先在影像的整体清晰度方面，LEE、增强型LEE和GAMMA_MAP三种算法都使影像有了一定程度的模糊，小波NEIGHSHRINK阈值算法保持了更高的整体清晰度。其次在噪声滤除方面，小波NEIGHSHRINK阈值算法处理后的影像还遗留有少量斑点，而另外三种算法的噪声滤除就相对比较彻底和完全。然而，并不能把存在于影像上的所有斑点都看作是噪声，也有可能是地物突变点。第三在纹理和线性结构的保持方面，LEE、增强型LEE和GAMMA_MAP三种算法均损失了影像中部分细小的纹理和结构信息，因而产生了影像的过平滑现象，而小波NEIGHSHRINK阈值算法良好地保持了原影像的细节结构。综合以上三点，小波NEIGHSHRINK阈值算法的影像处理效果要优于另外三种。

图5 经过不同滤波器滤波处理后的SAR图像

图6 原图和图4各图中3号红色区域的放大显示

(其中(a)是原始影像，(b)是小波NEIGHSHRINK阈值算法影像，(c)是LEE算法影像，(d)是增强型LEE算法影像，(e)是GAMMA-MAP算法影像)

从图6中能够更清晰地对比不同滤波处理方法的结果。该区域属于朝向雷达照射方向的坡面，并由于透视收缩现象使其看上去比周围区域要亮得多，且受斑点噪声污染比较严重。比较四种算法的滤波结果可以看到，LEE、增强型LEE和GAMMA_MAP三种算法对斑点的去除比较干净，但同时也损失了较多的纹理细节信息作为代价，降低了影像的整体清晰度。(b)图中经小波NEIGHSHRINK阈值算法处理后的影像上仍可以见到少量斑点，但对原始影像上细小的结构和纹理细节都具有良好的保持，影像整体清晰度较高。因此，小波NEIGHSHRINK阈值算法在有效滤除噪声的同时保留了地面目标对雷达信号的后向散射特征。

图7 SAR图像不同滤波器的比值图像

在目视判读的基础上，利用比值图像、等效视数和归一化均值等基于统计的评价指标，从客观定量的角度衡量不同算法的滤波性能。图7中(a)图是图3左下角2号矩形框内的放大显示，看到该区域的线性结构和纹理信息比较丰富。另外四幅则分别表示该区域不同算法滤波前后的比值图像。在(1)式的假定前提下，理论上原始影像与滤波后影像的比值应为灰度均匀的随机噪声图。在图7中可以看到，(b)图图像的灰度随机而均匀，而另外三幅图的灰度都包含了不同程度的纹理结构信息，该部分信息均被当作噪声而予以滤除。因此，小波NEIGHSHRINK阈值算法最有效地保持了原始影像的信息。

表1 SAR图像滤波器性能比较图

由表1可知，增强型LEE和GAMMA_MAP两种算法的ENL值相差甚微，数值较大，小波NEIGHSHRINK阈值算法的ENL值最小，LEE算法居中。归一化均值保持指数表示的是均匀区域图像平均辐射值的保持效果，其值愈逼近1，则保持能力愈强。从数值上看，四种算法的值都非常接近1。综合分析以上各项评价指标的结果，得到以下几点：

(1)三种空间域算法对原影像的纹理结构信息都有一定程度的损失，以牺牲影像的细节结构信息作为降噪的代价，使影像整体有所模糊。就目前而言，小波算法在这个方面表现出了它的优势。

(2)三种空间域算法都能够比较彻底的滤除影像斑点，且等效视数的数值较大。然而，对影像斑点的去除并不是以越完全越好，存在于影像上的斑点并不全都是噪声，还可能是地物突变点，而这些点是希望被保留的信息。经小波NEIGHSHRINK阈值算法处理后的影像会有少量斑点被保留，这可通过对影像的后续解译作出判断。

(3)四种算法在有效降低噪声的基础上，都具有良好的影像平均值保持性能，归一化均值保持指数数值均逼近于1。相对来说，小波NEIGHSHRINK阈值算法较其它三种算法偏离1稍远些，但已可满足影像后续应用的要求。

5 结论及展望

本文把小波NEIGHSHRINK阈值思想应用于实际SAR影像的滤波处理中，从视觉效果来看，首先四种滤波器都能够有效地滤除影像中的斑点噪声；其次小波NEIGHSHRINK阈值算法对影像结构和纹理细节信息的保持明显优于LEE、增强型LEE和GAMMA_MAP三种算法，影像整体更加清晰。而后三种算法对影像都有过平滑现象，使得较多的纹理细节信息损失。从定量评价指标分析，小波NEIGHSHRINK阈值算法的比值图像是四种算法中灰度最均匀，纹理结构信息最不明显的，客观地验证了其对影像纹理细节信息的良好保持。而在等效视数和归一化均值保持指数方面，小波NEIGHSHRINK阈值算法的统计值相对其它三种算法，要偏小或偏离数值1稍远一些，这说明该算法的斑点噪声抑制能力和对图像平均辐射值的保持方面偏弱。产生这种现象的主要原因是设置的通用阈值无法满足每一子带上小波系数的分布特性。方法的改进还需要从小波基的选取、小波分解级数的设置、阈值的设定和阈值函数的建立等方面进行综合考虑，这些都有待更进一步的深入研究。但不可置否的是，小波NEIGHSHRINK阈值算法在影像结构、纹理细节信息保持方面拥有其它三种对比空间域滤波方法无可比拟的优势，这对于含有独特和丰富纹理信息且更关注影像细节的SAR应用有着深远的意义。

虽然目前小波滤波的理论发展已经比较完备，而且也已经被成功应用到了多种领域，但仍有很多问题还值得关注和有待解决。

(1)实际SAR影像滤波应用滞后于小波滤波理论的发展。部分小波滤波方法的应用研究还停留在仿真实验阶段，而对实际影像作降噪处理是为影像的后续应用服务的，因此对滤波算法会提出一些针对性的要求。所以在今后的研究中应努力做好理论与实践的有力衔接，理论的发展应以切实解决实际应用工程中显现出来的问题为目标。

(2)一种特定的滤波方法不可能适用于整幅SAR影像的地表覆盖区。地球表面地物种类繁多，地形变化多样，同一幅SAR影像中往往可能同时存在地物类型主要以植被为主的高地形起伏区和以人工建筑物为主的平坦区。因此对同一幅影像的降噪处理可结合多种滤波思想，针对不同区域的地形地物特征，采用不同的算法以求达到最优效果。这也是值得研究的一个方向。

(3)SAR的成像机理与多光谱和红外光传感器完全不同，该系统是测量发射和返回脉冲的功率比，因此影像灰度及灰度空间变化所构成的纹理就是从雷达图像中提取信息的主要依据，包含独特而丰富的纹理信息是其不同于其它遥感影像的特征。而地表对雷达脉冲的反射信号不仅与地物本身的复介电常数、含水量、粗糙度等物理性质有关，同时也受到坡向、坡度等地形因子的影响[25]，尤其是在高地形起伏的山区，地形因素复杂。所以滤波算法的设计应该将地形因子的影响也考虑在内，遗憾的是本文的研究也并未对该问题作更深一步的讨论。目前，国内在这个问题上也很少有相关的报道，今后的研究将在该问题上作更深入的探讨。

(4)滤波效果的评价。对滤波后影像的质量评价是十分关键的，但是目前并没有一套公认的质量评价体系，使得方法的选择缺乏指导准则。这还有赖于实际工程应用的具体要求和有效的数学描述。

[1] 李震,廖静娟.合成孔径雷达地表参数反演模型与方法[M].北京:科学出版社,2011.

[2] GUO H，ODEGARD J E，LANG M，et al.Wavelet based speckle reduction with application to SAR based ATD/R[C].Image Processing,1994.Proceedings.ICIP-94.，IEEE International Conference.1994(1):75-79.

[3] RUIKAR S D，DOYE D D.Wavelet Based Image Denoising Technique[J].International Journal of Advanced Computer Science and Applications，2011，2(3):49-53.

[4] 李柯材.图像去噪的研究—基于中值滤波和小波变换的图像去噪应用研究[D].无锡:江南大学，2011.

[5] 潘泉,孟晋丽,张磊,等.小波滤波方法及应用[J].电子与信息学报，2007(1):236-242.

[6] CHEN G Y，BUI T D，KRZYZAK A.image denoising using neighboring wavelet coefficients[J].Integrated Computer-Aided Engineering，2005，12(1):99-107.

[7] CAI T T，SILVERMAN B W.Incorporating information on neighboring coefficients into wavelet estimation[J].Sankhya:The Indian Journal of Statistics,Series B，2001:127-148.

[8] LEE J S.Speckle suppression and analysis for synthetic aperture radar images[J].Optical Engineering，1986，25(5):255636-255636.

[9] 凌飞龙.SAR图像去噪及多源遥感数据融合算法研究[D].福州:福州大学，2004.

[10] 高贵,张军,吕信明,等.SAR图像乘性噪声模型分析[J].信号处理，2008，24(2):161-167.

[11] 汪新凡.小波基选择及其优化[J].株洲工学院学报,2003,17(5):33-35.

[12] KHARE A，KHARE M，JEONG Y，et al.Despeckling of medical ultrasound images using Daubechies complex wavelet transform[J].Signal Processing，2010，90(2):428-439.

[13] DAUBECHIES I.Orthonormal bases of compactly supported wavelets[J].Communications on pure and applied mathematics，1988，41(7):909-996.

[14] EDWARDS T.Discrete Wavelet Transforms:Theory and Implementation[J].Universidad de，1991.

[15] 程坚,王敬东,李鹏.SAR与可见光图像融合中小波基选择的研究[J].红外技术,2008，30(3):158-162.

[16] 李树钰.改进的小波阈值去噪方法及其在 MATLAB 中的仿真[J].噪声与振动控制,2010(2):121-124.

[17] 张波，季民河，沈琪.基于小波变换的高分辨率快鸟遥感图像薄云去除[J].遥感信息,2011(3):38-43.

[18] DAUBECHIES I，李建平,杨万年.小波十讲[M].北京:国防工业出版社,2004.

[19] 孙增国,韩崇昭.SAR图像MAP降噪的精细研究[J].小型微型计算机系统,2008,29(9):1736-1739.

[20] LOPES A，TOUZI R，NEZRY E.Adaptive speckle filters and scene heterogeneity[J].Geoscience and Remote Sensing，IEEE Transactions on，1990，28(6):992-1000.

[21] 李莹,郑永果.一种改进的增强 Lee 滤波算法[J].计算机应用与软件，2012,29(7):243-245.

[22] 黄海燕,王瑛.一种改进的SAR图像LEE滤波算法[J].遥感信息，2010(5):26-29.

[23] 韩春明，郭华东,王长林.SAR图像斑点噪声抑制的本质[J].遥感学报，2002,6(6):470-474.

[24] 王志勇，张继贤,黄国满.高分辨率SAR影像斑点噪声滤除方法的研究[J].测绘科学,2004,29(6):41-44.

[25] 倪玲，张剑清,姚巍.基于小波的SAR影像纹理分析[J].武汉大学学报(信息科学版),2004,29(4):367-370.