基于图论的船舶海水冷却管网水力特性
2014-02-03李宝仁仇艳凯廖金军
李宝仁,曹 博,仇艳凯,廖金军,刘 真
(华中科技大学 机械科学与工程学院,湖北 武汉 430074)
0 引 言
船舶海水冷却系统网络具有复杂网络拓扑关系,图论作为流体网络分析的重要手段,在流体网络水力计算中具有明显优势。基于图论理论建立描述流体网络固有参数的流体网络模型,将流体网络转换为对应的网络节点图,利用流体网络的矩阵形式来描述,不但使流体网络方程形式简单,而且使得流体网络系统及其水力特性本身的物理性质更加直观。
国内外学者对图论在流体网络中的应用进行了广泛研究。Velitchko G.Tzatchkov[1]等将图论用于城市供水功能分区流体网络中,并对其算法进行验证。Deuerlein, Jochen[2]提出利用线性图论理论来提高供水管网的计算效率,其将供水网络分解为外部网络和内核网络,从而大大减小了矩阵大小和计算时间。Kumar, S.Mohan[3]等提出利用图论的方法来简化分布供水网络的维数,从而提高供水网络状态估计的计算效率。Jinxue Sui[4]等基于图论及不可压缩流体N-S方程建立了流体网络非线性最小化模型,并将该模型应用于小脑循环网络参数的计算及血管分支流量及压力的控制。Milos,T.[5]提出利用图论来规划城市供水管网的最优路径,以实现成本最小化。Di Nardo, Armando[6]提出将图论应用于分区测量供水网络的设计中,以方便确定管网中流量计和边界阀的位置。Shen, Renjie[7]等提出利用图论寻找供水网络中工作在最大设计能力的管道支线,也就是确定供水管网的设计瓶颈。肖益民[8]等运用图论对流体输配管网的计算机分析进行了初步研究,并开发了相应计算程序。李祥立[9]等利用图论理论对枝状供热管网水力工况进行了模拟分析。曹慧哲[10-11]等基于图论对多定压节点管网水力计算方法进行了研究,推导了采用链支流量矩阵进行管网水力计算的解析表达式。杨开林[12]应用矩阵分析方法推导了渠网非恒定流数学模型,并将其应用于实例。赵进勇[13]运用图论连通度理论将河道-滩区系统概化为网络图模型,实现了对河道-滩区系统在一定水位条件下的连通状况模拟和连通程度定量分析。史成军等[14]采用模块化图形建模方法,对船舶中央冷却系统进行了建模仿真,并将其应用于轮机模拟器的研制中。贾志强等[15]应用SIMPLE算法对船舶中央冷却系统水力管网进行了动态模拟,利用不同时间步的结果动态反映了管网特性。但以往研究多忽略雷诺数的变化对管网支路阻力系数的影响。本文将图论理论应用于船舶海水冷去网络研究中,以某船舶典型海水冷却系统网络为研究对象,建立系统网络模型,并在网络解算中考虑雷诺数对管路阻力的影响,采用“变流阻系数”解算算法,大大提高了海水冷却管网水力分析与计算的精度。
1 船舶海水冷却网络模型建立
某船舶海水冷却管网主要由海水泵、舷侧阀、截止阀、截止止回阀和海水冷却用户组成。按照图论建模方法,根据模拟系统工作原理图,简化和抽象模拟系统网络中具体的动力元件和管路附件,使其只含有网络连接拓扑关系和节点元素的网络图,同时,将该海水冷却系统进行图论建模。其网络有向图如图1所示。
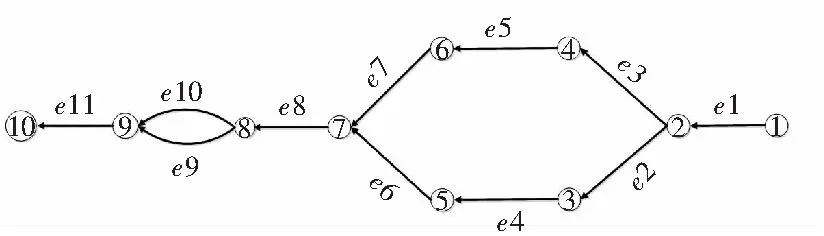
图1 船舶海水冷却系统开环网络图Fig.1 Open-loop network of seawater cooling system of ship
从图1可看出:该海水冷却系统网络图G1=(V1,E1)是具有节点集合V1={1,2,3,…,10}和分支集合E1={1,2,3,…,11}的单源单汇流体网络。其节点邻接矩阵A1=(a1ij)10×10满足关系为:
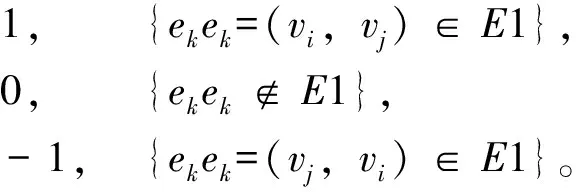
(1)
由式(1)可得到该海水冷却系统流体网络节点邻接矩阵为:

在流体网络中,源点和汇点之间一般保持流量平衡,即流入源点的总流量等于流出汇点的总流量。为了使流体网络能够方便地利用图论理论解算,需要将有源有汇网络化为无源无汇网络。
通过在图1中源点(节点1)和汇点(节点10)之间建立虚拟分支连接,形成无源无汇流体网络G1′=(V1′,E1′), 如图3所示。

图2 船舶海水冷却系统闭环网络图Fig.2 Close-loop network of seawater cooling system of ship
由式(1)可以得到该无源无汇网络节点邻接矩阵为:

表1船舶海水冷却系统网络图对应设备
Tab.1 The devices corresponding to the branches in the network of seawater cooling system

网络支路对应设备支路始节点支路末节点e1舷侧阀1、截止阀1、海水滤器①②e2截止阀2②③e3截止阀2②④e4海水泵③⑤e5海水泵④⑥e6截止止回阀⑤⑦e7截止止回阀⑥⑦e8无设备⑦⑧e9截止阀2、截止止回阀⑧⑨e10截止阀2、截止止回阀⑧⑨e11截止阀3、舷侧阀2⑨⑩
2 流体网络解算2.1 流体网络解算算法
根据图论理论,全船海水冷却系统网络图G=(V,E), 其网络节点数m=V, 网络分支数n=E, 系统网络图G的基本关联矩阵B′和基本回路矩阵C′的秩分别为rank(B)=m-1和rank(C′)=n-m+1, 根据流量守恒方程,如果定义系统流体网络各分支流量为未知数,则通过系统网络图基本关联矩阵可以构造出m-1个线性无关的n元一次方程组,同理,根据能量守恒方程,确定系统网络各分支流阻值后,利用系统网络图基本回路矩阵可以构造出n-m+1个线性无关的n元二次非线性方程组,于是联立流量守恒和能量守恒方程可得到(m-1)+(n-m+1)=n个n元线性无关的方程组:
(2)
式中:bij和cij分别为全船海水冷却系统网络图G的基本关联矩阵Bk和基本回路矩阵Ck的元素;qj为系统网络分支流量;fi为回路阻力平衡方程;f(ri,qj,Re)为回路各分支动态阻力矩阵。
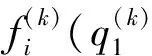
(3)

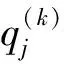
(4)
忽略2阶以上无穷小项,将式(3)写成矩阵形式,得:

(5)
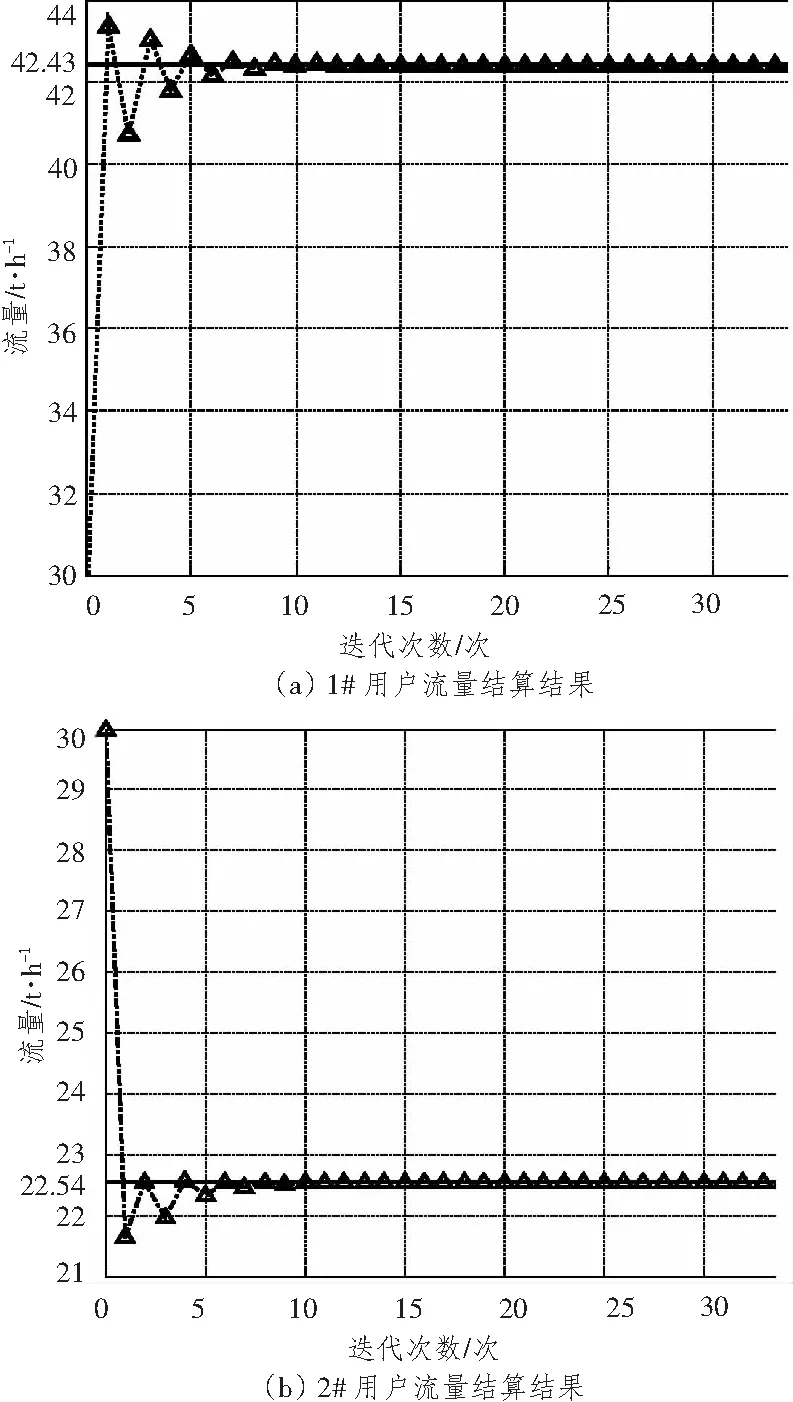
由式(5)可得其流量修正矩阵为:
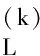
(6)
采用第k次迭代后余支流量修正矩阵和第k次迭代后回路阻力函数矩阵的行和范数作为迭代误差的判别条件:
(7)
2.2 变流阻系数网络解算原理
以全船海水冷却系统网络为主要研究对象,由于其系统网络内流体流动状态较复杂,不同工况下,层流、紊流和过渡流都有可能同时存在。因此,从提高系统网络解算精度出发,本文提出采用变流阻系数迭代法,在计算过程中动态更新系统网络各分支管路中雷诺数的计算。
沿程水头损失计算公式为[16]:

(8)
确定沿程水头损失,最重要是要确定沿程阻力系数。沿程阻力系数λ=f(Re,e/d), 是雷诺数Re与相对粗糙度e/d的函数。
当雷诺数Re<2 300时:

(9)
当4 000 (10) 在4 000 (11) 当处于完全粗糙管区时: (12) 当处于紊流过渡区时: (13) 式(13)是隐式公式,不便于计算,可由下式近似替代: (14) 某船舶海水冷却系统工况1为双泵双支路开工况,即同时启动1#和2#海水泵,且同时开启1#和2#海水用户。在解算过程中,将海水泵和海水用户支路流量初始化为30 t/h,按照网络解算方法,系统双泵双支路开工况下1#和2#海水用户支路流量解算结果如图3所示。 图3 工况1网络流量解算结果Fig.3 Results of the network in the first workingcondition 从图4中可以看出,在系统双泵双支路工况系统网络解算中,1#用户支路流量解算经过34次迭代后,余支修正矩阵和回路阻力函数矩阵行和范数小于10-5,收敛值为42.43 t/h;2#用户支路流量经过迭代后收敛值为22.54 t/h。虽然系统分支初始化流量与收敛值相差较大,但是迭代过程中迭代值迅速接近收敛值,并很快达到解算收敛条件,从而说明系统网络迭代算法稳定性和收敛性较好。 某船舶海水冷却系统工况2为单泵双支路开工况,即启动1#海水泵,开启1#和2#海水用户。在解算过程中,将海水泵和1#、2#海水用户支路流量分别初始化为30 t/h,15 t/h和15 t/h,单泵双支路开工况下1#和2#海水用户流量解算结果如图4所示。 图4 工况2网络流量分配解算Fig.4 Results of the network in the secondworkingcondition 当仅启动1#泵,开启1#和2#海水用户时,系统网络解算经过13次迭代后收敛,1#、2#用户支路流量值分别收敛为27.72 t/h和14.75 t/h,此时1#海水泵的流量为42.47 t/h。 某船舶海水冷却系统工况3也为单泵双支路开工况,即启动2#海水泵,开启1#和2#海水用户。在解算过程中将海水泵和1#、2#海水用户支路流量分别初始化为30 t/h,15 t/h和15 t/h,单泵双支路开工况下1#和2#海水用户支路流量解算结果如图5所示。 图5 工况3网络流量分配解算Fig.5 Results of the network in the thirdworkingcondition 当仅启动2#泵,开启1#和2#海水用户时,系统网络解算经过13次迭代后收敛,1#、2#用户支路流量值分别收敛为26.62 t/h和14.65 t/h,此时2#泵流量为41.37 t/h。 船舶海水冷却管网试验系统主要测试流体网络各用户实际用水量。试验系统采用2台额定流量为25 t/h的海水泵,数据采集卡选用PCI-1710 HG,涡轮流量传感器精度为0.2 FS,量程为:4~100 t/h,耐压6.3 MPa,输出电流范围:4~20 mA,24 V直流供电,压力传感器精度为0.2 FS,量程为:0~0.6 MPa,输出电流范围:4~20 mA,24 V直流供电。 图6 试验系统原理图Fig.6 Schematic view of the test 通过对该系统各支路流量测试结果和系统网络各支路流量解算结果的对比发现,实测结果与解算值的最大偏差为2.45%,最小偏差达0.07%。试验结果验证了船舶海水冷却系统“变流阻系数”网络解算的精准性。 表2 工况1网络解算结果与试验结果对比 表3 工况2网络解算结果与试验结果对比 表4 工况3网络解算结果与试验结果对比 1)将图论理论应用于船舶海水冷却管网的计算,引入虚拟分支后,可将有源有汇网络化为无源无汇网络,使海水冷却网络只包含流体管路的连接拓扑关系,以便利用矩阵形式将其物理属性方便地表达,大大降低了求解难度。 2)本文提出的流体系统网络解算“变流阻系数”迭代方法,在迭代过程中不断修正流量对系统阻力的影响,经过有限次迭代后计算结果可以迅速收敛,系统网络解算误差均在3%以内。 3)通过试验测试与网络解算结果对比发现,二者具有较好的一致性,验证了“变流阻系数”网络解算算法的有效性和可行性。 [1] VELITCHKO T G.Alcocer-Yamanaka,Victor H.;Bourguett Ortíz,Víctor.Graph theorybased algorithms for water distribution network sectorization projects.8th Annual WaterDistribution Systems Analysis Symposium 2006,August 27,172. [2] JOCHEN D.Efficient supply network management based on linear graph theory.8th Annual Water Distribution Systems Analysis Symposium 2006.2007,63. [3] MOHAN K S,SHANKAR N,MURTY B S.State estimation in water distribution networks using graph-theoretic reduction strategy.Journal of Water Resources Planning and Management[J].2008,134(5):395-403. [4] SUI Jin-xue,HU Yun′an,LI Yang,ZHEN Hua.A hemod-ynamics minimal model for the cerebral circulation of willis based on graph theory.2008 2nd International Conference on Bioinformatics and Biomedical Engineering (ICBBE′08), 2008:1796-1799. [5] Milos,T.Dobanda˘ E.;Manea,A.;Badarau, R.; Stroit,a˘,D.Computational graph theory for find out optimal routes of pipeline supply[C].IEEE 8th International Conference on Computational Cybernetics and 9th International Conference on Technical Informatics.(ICCC-CONTI 2010).2010:577-580. [6] ARMANDO D N.MICHELE D N.A heuristic design su-pport methodology based on graph theory for district metering of water supply networks[J].Engineering Opti-mization.2011,43(2):193-211. [7] Shen,JIA Ren-jie,LIANG Qing-gang,ZHANG Yan-yan,Jing.Identify the bottleneck of water network by using graph theory[J].Advanced Materials Research.2012,433-440,4794-4797. [8] 肖益民,付祥钊.用MTLAB 分析流体输配管网的初步研究[J].重庆大学学报(自然科学版),2002,25(8):14-17. [9] 李祥立,王晓霞,周志刚,等.枝状供热管网水力工况模拟分析[J].煤气与热力,2004,24(10):554-557. [10] 曹慧哲,贺志宏,朱蒙生,等.基于图论的多定压节点管网水力计算方法的研究[J].给水排水,2008,34(1):105-108. [11] 曹慧哲 ,贺志宏,何钟怡.基于图论的环状管网慢变流的计算研究[J].哈尔滨工业大学学报,2007,39(10):1559-1563. [12] 杨开林.渠网非恒定流图论原理[J].水利学报,2009,40(11):1281-1289. [13] 赵进勇,董哲仁,翟正丽,等.基于图论的河道-滩区系统连通性评价方法[J].水利学报,2011,42(5):537-543. [14] 史成军,郭晨,沈智鹏.船舶中央冷却系统管网的建模与仿真方法[C].第五届全国仿真器学术会,2004:277-282. [15] 贾志强,董葳.船舶中央冷却系统水力管网动态模拟[J].船舶工程,2012,34(3):43-46. [16] 严煦世,刘遂庆.给水排水管网系统(第二版)[M].北京:中国建筑工业出版社,2008.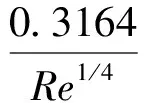



3 网络解算结果分析


4 试验分析
4.1 试验原理
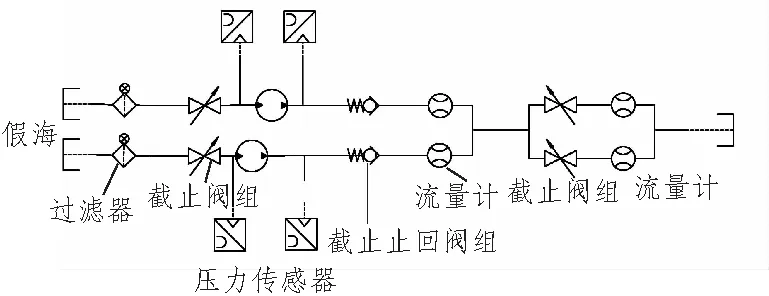
4.2 试验结果分析



5 结 语
