改进CCRP疏散算法在船舶与海洋工程中的应用

余建星，周健状，柴 松，梁 静，张 谦

(天津大学 水利工程仿真与安全国家重点实验室，天津 300072)

0 引 言

近年来,国际能源市场发生了重大的历史变化，国际油价持续上升，屡创历史新高,海洋石油一跃成为重要的战略资源。海洋石油的开发在近年的不断摸索和研究中取得长足的进步。目前，海洋石油开发主要依靠海洋平台和FPSO进行油气勘探、采集和加工等活动。海洋作业平台上，作业种类多样，生活区工作区划分复杂，路径也相对曲折，一旦发生紧急事件，容易造成人员恐慌、拥挤踩踏和伤亡。本文针对海洋平台以及船舶甲板，提出突发事件下的紧急疏散方法，以尽可能短的时间完成疏散过程，在最大程度上保证人员安全。

紧急疏散是指飓风、海啸等自然灾害以及火灾、爆炸泄漏等突发事件条件下，将处于危险区域的人群快速疏散至安全地点。国内外的诸多学者采用不同方法对此进行了研究。现行的疏散方法大体分为计算机仿真和路径规划两类。计算机仿真基于疏散需求对运行过程进行随机模拟，常用软件如DYNASMART和DynaMIT。但对大规模运输网络，模拟过程耗时长。

路径规划方法多基于网络流算法。Hamacher等综述了疏散问题的宏观模型，将时间作为主要因素，给出了多个疏散数学模型[1]。高明霞等将交通管制措施考虑在内，将疏散路线的优化描述为分方向点权网络中的最小费用流问题，提出基于图形表示，在分方向点权网络中寻找最小费用流的改进最小费用路算法[2]。张江华等基于启发式算法利用网络优化思想，研究了存在优先顺序的多源点和容量受限的应急疏散[3]。杨建芳等利用最短路径尽可能饱和疏散的思想，设计出多出口建筑物突发事件应急疏散算法，通过对网络进行不断更新来确定每条路径实际流量，从而确定最优疏散方案[4]。Lu，Huang和Shekhar三位学者提出了2个启发式的容量受限的原型算法,即SRCCP和MRCCP，并且使用小型网络对它们做了性能测试[5]。SRCCP为每个起始结点指定了一条可用路径，它虽具有较快的运行时间，但效果很差。MRCCP为每个起始结点分配了多条路径，解的质量不错，同时相对线性规划法来说，具有较少的时间成本。但MRCCP在一些大型道路网络上由于计算成本较大效果不太令人满意。后来，以上三位学者又对其进行改进，提出了CCRP算法[6]。CCRP算法利用基本的网络拓扑图和容量限制属性来生成一个次优的疏散方案，它以最短疏散时间为算法的最终目标。CCRP算法可以将时间成本降低到0(p·nlogn)。

上述研究往往针对不同的背景建立差异化模型。本文基于CCRP算法，针对船舶与海洋工程中的特点，研究紧急疏散的模型和算法实现。

1 问题描述

已知：

一赋权网络图G=(poi,edg)表示疏散空间的连接和节点布置情况，poi是节点集合，edg是边集合；

每个节点的2个属性：节点容量cap_poi和初始疏散人数ini_num；

每条边的2个属性：边容量cap_edg和权重c。边容量cap_edg是在任一时刻，该条边可同时容纳的疏散人数的最大值；权重c是疏散者通过该条边所需的时间；

总疏散人数以及疏散人员在建筑物内各个节点的布置情况ini_num；

疏散起点数量和标号、终点数量和标号；

紧急事件类型，范围，影响程度。用来求解当量长度；

假设终点容量无限大。

求解：紧急疏散方案(包括：若干条从起点到终点的路线；不同疏散路线的疏散人数；不同疏散人群在到达各个路线节点的时刻以及等待时间)。

目标：疏散总时间最短。

原则：先进先出——即当2组疏散人员相遇，需要使用同一路径时，先开始疏散的人员优先通过。

2 CCRP疏散算法

CCRP算法是求解紧急疏散问题的启发式算法的典型代表。它能在相对较低的计算成本下，求解得到质量损失较小的疏散方案。一般而言，由CCRP计算得到的解的质量与线性规划最优解的偏差不超过10%，而计算时间却只需要线性规划求解时间的一半以内。同时，CCRP算法对疏散人数、起点规模以及网络规模具有可拓展性。

CCRP算法的基本思想是，将节点可用容量和边可用容量模拟成随时间变化的系列值，使得更接近实际疏散过程中的节点和边的情况。使用Dijkstra最短路算法找到最短路径并不断修正节点和边可用容量。计算中，将每个疏散起点的疏散者分成若干小组，并为每个小组指定疏散路径和时刻表。根据路径的容量限制，为每条路径预留流量。基于新的路径容量，重新计算最短路，直到所有疏散者疏散完毕。

3 改进的CCRP疏散算法

3.1 抽象疏散网络图

抽象疏散网络图将实际布置图和疏散网络图联系在一起，对于海洋平台等小范围疏散对象的疏散过程非常重要。笔者查阅大量文献，没有找到说明抽象网络图的相关资料。以下是笔者根据反复试验总结出的网络图的抽象方法，难免有不足之处，有待完善。

抽象疏散网络图大体分为划分节点、确定边以及相关参数设置3个步骤。通常划分节点和确定边2个步骤同时进行。

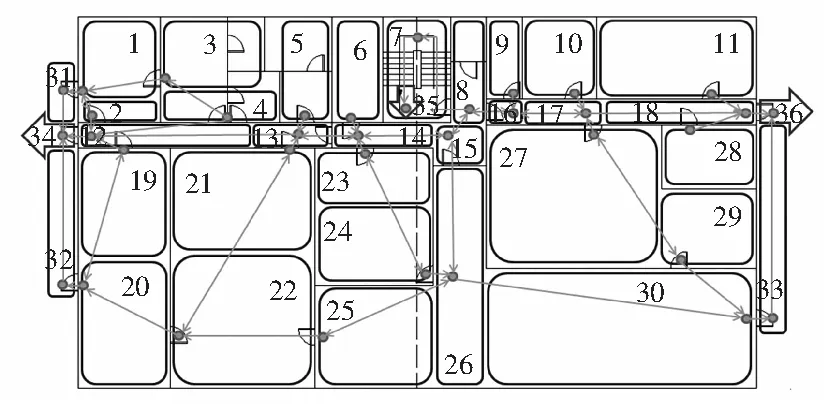
网络图中的节点与实际海洋平台上的房间划分并不完全一致。网络图中的节点划分，一方面受到实际平台上的房间划分的影响，一方面与各个房间的出口布置有关。节点划分的基本原则是：① 每个房间首先划分为1个节点，再根据房间出口布置和数量将该节点划分为若干节点；② 每个节点有1个节点中心，代表节点的实际位置，一般设置在节点的出口处；③ 边是有向边，连接2个节点中心，代表2个节点之间的连接情况；④ 当2条边有冲突时，通过额外划分虚节点解决；⑤ 边的方向以疏散到出口为准，当无法确定时，允许出现双向边；⑥当网络图过于复杂时，可简化处理。当若干个房间互相之间的连通性较好，整体面积不大，而且整体和外界相对封闭，没有过多的出口时，可以将这若干个房间作为一个整体处理，不考虑整体内部的房间布置情况，只考虑整体的出口，划分为与出口数相等的节点数，节点中心一般设置在该整体的出口处。

相关参数设置主要指边参数和点参数的设置。边参数又包括边通过时间和边通量2项内容。边通过时间和边总长度成正比；边通量与边的最小宽度成正比。点参数包括节点容量和节点初始疏散人数2项内容。节点容量与节点大小、用途有关。节点初始人数是随机的。

以上工作完成，将相关参数标识在节点和边上，可得到疏散网络图。

3.2 当量长度概念的应用

紧急疏散往往是应对某些紧急事件，如火灾、爆炸、毒气泄漏等。紧急事件的发生，一方面提出了紧急疏散的必要性，另一方面，也会影响到疏散的结果。具体表现为：处于危险区域的疏散路径，很可能不再适于人员通行，或者人员通过危险路径的难度增加。传统的CCRP算法能有效解决紧急疏散问题，但却没有将紧急事件的影响考虑在内。

本文对此进行改进的基本思想为：针对特定的紧急事件，修改路径信息，引入当量长度的概念[7]。

第i条路径的当量长度

li=ki·ωi·lri。

式中：ki=v1i/v2i，ki为疏散路径i的通行难度系数，v1i为正常通行速度，v2i为特定疏散情况下的通行速度；ωi为危险系数，表征路径i的危险程度，与紧急事件的类型、发生地点、影响范围等有关，ω∈[1,+∞)；lri为路径i的实际长度。

此外，当紧急事件发生时，危险区域的范围和危险程度都随时间变化。为了模拟该现象，令当量长度是随时间和空间变化的函数，该函数受到疏散区域通风条件和布置情况等的影响。即li=f(w,a,e)，w是通风条件，a是布置情况，e是其他条件。

3.3 双向边的应用

传统的CCRP算法，针对单向有向网络图。但在实际疏散网络中，由于各个节点中人数的随机性，常不能确定疏散过程中各条连接边的疏散方向。为此，本文引入双向边，以证明CCRP算法在双向边条件下仍适用。

证明：CCRP算法中，双向边的2个方向在实际疏散中不会发生冲突。

基于CCRP疏散算法的1次疏散过程中，1条边的2个方向不可能均被疏散使用⟹题目。

反证法：

假设，在基于CCRP疏散算法的疏散过程中，1条边的2个方向均被疏散使用。

图示假设情景：

图1 双向边示意图
Fig.1 Bidirectional edge

图1中，AB代表双向边，BD代表从B节点到达某一出口的路径，AC代表从A节点到达某一出口的路径。

存在如下2条疏散路径：A-B-D和B-A-C。2条路径的疏散人数分别是flowA和flowB，出发时刻分别是tA和tB， 且flowA,flowB≥1。

由此可证明，上述情景在实际疏散中不可能出现。

若tA≤tB(即flowA先出发)，根据CCRP的最短路原则，A-B-D路径都是tA时刻的最短路。

而由图易知，dBD

所以，ABD不是tA时刻的最短路，该结论与CCRP的最短路原则矛盾，tB≤tA时同理可证，

所以，图示情景不可能出现，即，在CCRP疏散算法的一次疏散过程中，1条边的2个方向不可能均被使用，题目得证。

3.4 改进的CCRP算法流程

综合上述对CCRP的改进方案，提出以下改进CCRP算法流程：

1)从海洋平台布置图中抽象出疏散网络图；

2)给网络添加超起点S0，用边连接超起点S0和其他起点。边容量是+∞，通过时间是0；

3)处理每条边，以当量长度代替实际长度。li=ki·ωi·lri；

4)当任一起点还有疏散人员时，应用Dijkstra最短路算法求解从超起点S0到任一终点的路径R。R满足：

① 在所有的起点到终点的路径中，通过时间最少；

② 路径上的每条边的可用边容量在对应时刻大于0；

③ 路径上每个节点的可用点容量在对应时刻大于0。

5)确定人流量flow。flow=min(节点处的疏散人员数量，可用边容量，可用点容量)。

6)修正边参数及点参数。可用边容量=可用边容量-flow；可用点容量=可用点容量-flow；

7)检查所有起点，是否还有未被疏散的人员。若有，返回第3步；否则，转到第8步；

8)疏散完成，输出疏散方案。

4 算例分析

假定一海洋平台或船舶甲板的布置图如图2所示。在该海洋平台或甲板的四周，是一圈逃生通道。各房间之间及与走廊的连接情况如图2所示。根据疏散网络图的绘制原则，得到节点划分路径连接情况及疏散网络图分别如图3～图4所示。

图2 布置图Fig.2 Map of layout

图3 节点划分以及路径连接情况Fig.3 Node divide and path connection

图4 疏散网络图(边长度为当量长度)Fig.4 Map of evacuation network

根据改进的CCRP算法，利用Matlab编程工具辅助计算，得到疏散方案如表1所示。该表详细给出了若干条疏散路径、每条路径的疏散人数、疏散者在不同节点的到达时间、等待时间、各条疏散路径的结束时间及疏散总时间等信息。

表1 疏散方案

以第3条路径为例说明：该路径上有1个疏散者，路径顺序是11-18-36。该疏散者在11节点上等待1个时间单位，然后从11节点出发，依次来到18节点、36节点，完成疏散。除了在11节点等待1个时间单位，疏散者在其他位置不做停留。该疏散者在该条路径上完成疏散的总时刻是第3个时间单位。

图5 典型节点疏散人数变化Fig.5 Changes of number of people in typical nodes

为了验证算法的有效性，图5给出了3个典型节点的疏散人数变化情况。节点12，24和36分别是中间节点、起点和终点。由图可知，节点12作为中间节点，该节点的疏散人数呈波动状态，这与该节点在不同路径中的使用情况有关；节点24是起点，该节点的疏散人数单调减少，疏散者不断从起点离开；节点36是终点，该节点的疏散人数呈单调增加状态，这表征疏散人员不断被疏散到该节点，与实际情况相符。此外，这3个节点在任一时刻的疏散人数均不大于其节点容量，符合实际情况。

5 结 语

本文针对海洋平台以及船舶甲板的紧急疏散问题，基于CCRP算法，提出了疏散网络图的绘制方法，并在计算中使用了当量长度、双向边2个概念，将紧急事件和疏散人员分布情况对疏散方案的影响考虑在内，给出了多起点、多终点、容量受限的疏散算法。通过算例验证了算法的有效性和可行性。文中的点参数、边参数、以及求解当量长度的有关参数，需要试验数据不断完善修正。

[1] HAMACHER H W,TJANDRA S A.Mathematical modeling of evacuation problems：a state of the art[C].Berlin:Springer,2002：227-226.

[2] 高明霞，贺国光.考虑交通管控影响的疏散组织措施优化研究[D].天津：天津大学，2007.

[3] 张江华，刘治平，朱道立.多源点突发灾害事故应急疏散模型与算法[J].管理科学学报，2009，12(3)：111-118.

[4] 杨建芳，高岩.多出口建筑物突发事件应急疏散模型和算法[J].系统工程理论与实践,2011，31：147-153.

[5] LU Qing-song,HUANG Yan.Evacuation planning:a cap-acity constrained routing approach[J].Department of Computer Science,2003：1-11.

[6] LU Qing-song,GEORGE B.Capacity constrained routing algorithm for evacuation planning: a summary of results[J].2005：291-306.

[7] 肖国清，温丽敏.基于遗传算法的毒气泄漏时最佳疏散路径的研究[J].湘潭矿业学院学报，2001，16(4)：9-12.