基于LS-SVM的水火弯板机械手逆运动学求解

李 彦， 王 玲

(江苏科技大学 电子信息学院，江苏 镇江 212003)

0 引 言

目前，造船工业中应用最广泛也是最关键的船板加工技术之一即是水火弯板成型技术。由于该工艺技术性强，难度大，操作技艺难以掌握，目前大型复杂曲面钢板水火加工在实际生产中主要由老技术工人来完成，这种人工方式严重制约造船事业的快速发展。

而在水火弯板智能控制系统中，机械手的应用将工人从繁重的体力劳动中解脱出来，大大提高了生产效率和加工精度，而且产生的噪声小。水火弯板工艺的自动化和智能化对提高船外板成型的质量和造船速度以及降低造船成本有着重要意义[1]。

本文主要研究水火弯板机械手的运动学问题。传统的求逆方法如代数法、几何法及迭代法这几种方法计算量大，有一定的限制[2]。本文采用最小二乘支持向量机LS-SVM算法对逆运动学进行求解，并与LMBP神经网络算法结果进行对比，仿真效果良好，符合弯板机械手的控制要求，为下一步动力学研究及实际使用奠定基础。

1 水火弯板机械手正向运动学

按照加工工艺的要求，机械手需要在全空间中进行作业，为了使所有运动都能实现，机械手要有6个自由度，本文研究的弯板机械手也采用六自由度。

机械手的正向运动学是已知6个关节的角度确定末端位姿的过程。首先用D-H[3]方法建立机械手的坐标模型。D-H分析方法用来描述机械手相邻两连杆之间的运动学关系：相邻两连杆的位姿用1个4×4的齐次变换矩阵进行描述，并由此推导出机械手末端夹持机构坐标系相对于底座参考坐标系的齐次变换矩阵，进而建立机械手的运动学方程和几何模型，具体如下：

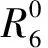
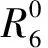
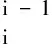
式中：θi为关节角度；di为偏移量；ai为连杆长度；αi为扭转角。

本系统中弯板机械手6个关节的运动范围分别为±15°，±30°，±60°，±100°，±120°，±160°，最大速度分别为30°/s，30°/s，30°/s，60°/s，60°/s，60°/s。D-H参数如表1所示。

表1 弯板机械手D-H参数

2 机械手逆向运动学

机械手的逆运动学是已知末端轨迹求解各个关节角度的过程，逆解求取是机械手运动学研究的难点。

传统求解机械手逆运动学的方法非常复杂，计算量大，且存在多解问题[4]。机械手逆运动学问题的求解方法大致可分成封闭解法与数值解法这两大类。其存在的主要问题是计算量大，受硬件结构的限制比较大，甚至可能得不到有效的逆解。

智能控制方法是现代控制方法的发展方向，主要包括遗传算法、神经网络算法及各种智能计算方法的组合形式。针对机械手的逆解求取，其求解思路是把机器人运动方程转化为一个控制问题来求解。机械手逆运动学是由笛卡尔空间到关节空间的转换，是典型的非线性映射问题。而BP网络是一种典型的单向传播的多层前向网络，适合解决非线性映射问题[5]。

2.1 基于LMBP的弯板机械手逆运动学

BP神经网络由输入层，隐含层和输出层3个层次组成，确定神经网络的结构即确定每层神经元的个数是算法的重点之一。

2.2 基于LSSVM的弯板机械手逆运动学

支持向量机的主要思想是：将选择的非线性映射从输入映射至高维空间，并且在这个空间中可以构造最优的决策函数。当构造最优的决策函数时，不仅利用结构风险最小化原则，而且将原来的核函数取代了高维特征空间中的点积运算[6-7]。

最小二乘支持向量机是对标准支持向量机进行的扩展之一，优化指标用的是平方项，而且用等式约束代替标准支持向量机中的不等式约束，从而推出了一系列的等式约束，故把二次规划的问题转化成为求解线性方程组的问题，不仅简化了计算的复杂性，而且求解速度相对有所增加[8]。LSSVM的优化目标采用的是ξi的平方项，所以优化问题如下式：

(2)

s.t:yi=ωTψ(xi)+b+ξi,i=1,…,n。

(3)

下面引入拉格朗日函数求解式(2)的优化问题，

b+ξi-yi}。

(4)

式中ai为拉格朗日乘子。根据KTT优化条件有：

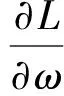
得到以下等式约束条件：

ωTψ(xi)+b+ξi-yi=0。

对于i=1,…,n，消去ω，ξ可得线性方程组：

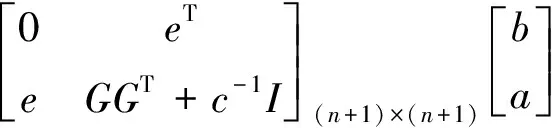
式中：e为元素为1的n×1向量；I为n×n的单位阵。

a=[a1,a2,…,an]T,y=[y1,y2,…,yn]T,

G=[ψ(x1)T,ψ(x2)T,…,ψ(xn)T]。

根据Mercer条件，定义核函数如下：

K(xi,yi)=ψ(xi)Tψ(xj)。

(6)

综上，该方程组为：

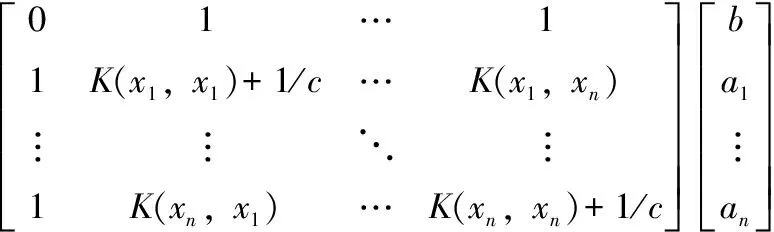
(7)

式(7)的线性方程可用最小二乘法求出a和b， 则线性回归函数为

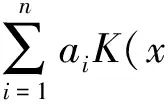
(8)

通常核函数采用径向基函数:

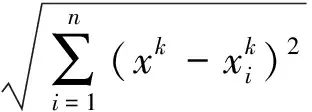
最小二乘支持向量机通过有约束的二次优化方法确定网络的隐含层节点个数和网络权值，这种映射与感知器和径向基神经网络(RBF)的形式相似，不同的是神经网络的结构和权值初值的选取决定了网络的训练速度和收敛特性，而最小二乘支持向量机的这种形式决定了其优越特性。

3 仿真验证

为验证所用算法在水火弯板机械手求逆运动学中的有效性，本文进行了相关的仿真实验。

3.1 正向运动学仿真

首先在Matlab中建立机械手的模型，进行正运动学的仿真实验。

在各关节允许的范围内给予机械手的初始角度q1=[0 0 0 0 0 0]和终点角度q2=[5.120 -15.362 46.885 82.653 100.996 -122.542]。机械手运动过程平稳，图1是当给予上述初始和终点角度后，机械手在空间中走出的一段平滑轨迹，由此可以验证弯板机械手模型建立的正确性和有效性。

图1 机械手运动轨迹图Fig.1 Trajectory of manipulator

3.2 逆向运动学仿真

根据各关节角的变化范围以及机器人实际工作要求确定各关节角的变化范围。根据“多移动小关节少移动大关节”的选取原则，结合实际操作的需要，在各关节允许的角度范围内随机产生1 000组角度值，其中θ1的取值范围限定为(-5，+5)，θ2为(-5，+5)，θ3为(-10，+10)，θ4为(-15，+15)，θ5为(-30，+30)，θ6为(-60，+60)， 单位为(°)。

从而得到了1 000组输入输出数据，980组作为训练样本，20组作为测试样本。LMBP神经网络的训练函数为trainlm，当训练步数为231时达到误差精度范围。用20组数据对网络进行测试，图2为关节6预测值与期望值的比较及误差曲线。

图2 关节6的LMBP预测值与期望值Fig.2 Expected and neural network prediction output of the sixth joint angles

图3 关节6的LMBP误差曲线Fig.3 Error curve of the sixth joint angles of neural network

由图2和图3可看出，神经网络虽然可以近似地实现逆解的求取，但误差较大，部分角度甚至达到10°，不能满足弯板机械手精度要求。

针对存在的误差，本文重点设计了LS-SVM即最小二乘支持向量机，对机械手逆运动学进行求解分析。样本同LMBP神经网络的选取方法相同，980组作为训练学习样本，20组作为测试样本。图4～图7分别为用LS-SVM方法时，关节5和关节6的期望值与输出值比较及误差曲线图。

图4 关节5的LSSVM预测值与期望值Fig.4 Expected and LSSVM prediction output of the fifth joint angles

图5 关节5的LSSVM误差曲线Fig.5 Error curve of the fifth joint angles of LSSVM

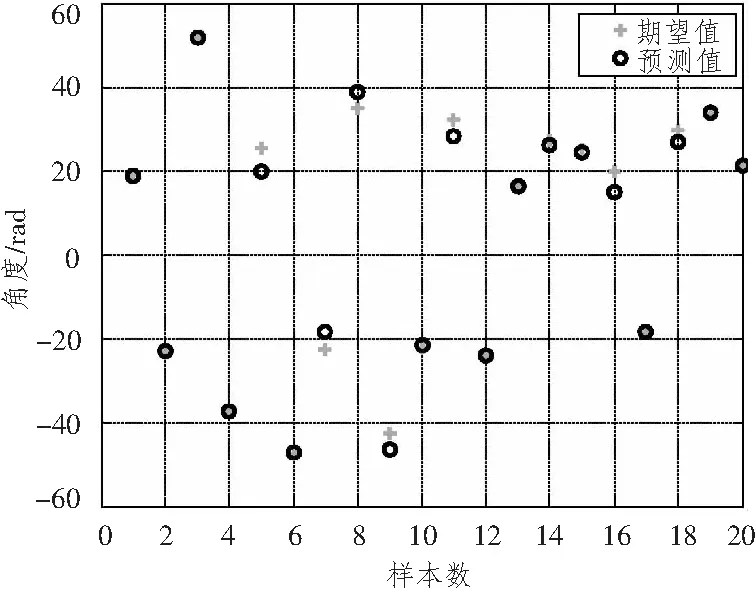
图6 关节6的LSSVM预测值与期望值Fig.6 Expected and LSSVM prediction output of the sixth joint angles

图7 关节6的LSSVM误差曲线Fig.7 Error curve of the sixth joint angles of LSSVM

由图4～图7可以看出，采用最小二乘支持向量机算法求得的关节5的误差在0.6°范围内，而关节6的误差也降低到5°以下，比LMBP的求解精度有明显的提高。

用此算法将求得的关节角度给予机械手，由正运动可以得到机械手末端轨迹，如图8所示。由图可看出，跟踪误差在±3 mm范围内，效果良好，能够满足弯板机械手对加热轨迹的精度要求。

图8 弯板机械手末端轨迹跟踪效果Fig.8 Tracking results of bending robot

4 结 语

本文利用D-H方法对水火弯板机械手进行了运动学的建模，并在Matlab中进行了仿真，验证了模型建立的正确性。重点对逆运动学进行了相关探讨，首先运用神经网络LMBP对机械手逆模型进行模拟，基本实现了由末端轨迹到关节角度的映射。针对存在的误差，重点介绍了最小二乘支持向量机LS-SVM的应用。根据各个关节角度的变化范围，随机产生训练样本对模型进行学习，并通过测试样本验证了此方法的可行性和优越性。由仿真结果可以看出，LS-SVM的应用使得系统精度提高，误差减小，很好地对水火弯板机械手逆运动学进行了求解，最终实现末端轨迹的良好跟踪。

[1] 廖忠凯.水火弯板成型单悬臂机器人设计分析[D].大连：大连理工大学,2006.

[2] 倪骄骅，赵忠伟，孙美艳.基于代数算法神经网络在机器人逆运动学中的应用[J].制造业自动化,2009,31(8):179-183.

NI Xiao-hua，ZHAO Zhong-wei，SUN Mei-yan.Neural network based on algebra algorithm applying to inverse kinematics of robot manipulator[J].Manufacturing Automation,2009,31(8):179-183.

[3] 彭疆，周国荣.基于神经网络的机器人逆运动学算法[J].企业技术开发,2005,24(3):30-32.

PENG Jiang，ZHOU Guo-rong.Arithmetic of inverse kinematics of robots based on neural networks[J].Technological Development of Enterprise,2005,24(3):30-32.

[4] 王耀南，印峰，夏汉民.多关节机器人逆运动学问题的实时求解[J].中国机械工程,2010,21(10):1143-1148.

[5] 王求.焊接机械手的运动学分析和仿真[D].合肥工业大学,2011.

[6] 杨延西，刘丁，辛菁.基于LS-SVM的机器人逆运动学建模[J].系统仿真学报,2006,18(5):1260-1263.

YANG Yan-xi,LIU Ding,XIN Jing. Inverse kinematics of robotic manipulators based on LS-SVM[J].Journal of System Simulation,2006,18(5):1260-1263.

[7] 张雪峰.最小二乘与最小二乘支持向量机[D].成都：电子科技大学,2007.

[8] 方辉，王倩.支持向量机的算法研究[J].长春师范学院学报，2007,26(3):90-91.

FANG Hui,WANG Qian.Support vector machine algorithm[J].Chang Chun Teachers College,2007,26(3):90-91.

[9] MATLAB中文论坛.MATLAB神经网络30个案例分析[M].北京:北京航空航天大学出版社,2010.