圆柱体惯性力系数和阻力系数随雷诺数和邱卡数变化曲线拟合

陈 靖，朱克强

(宁波大学 海运学院， 浙江 宁波 315211)

0 引 言

近海平台和海底管系的各结构部件经常暴露在海水中，分析和计算波浪对海洋结构物的作用力是进行此类海洋结构物设计建造的基础。当管件或者结构部件的直径与该处波浪波长的比率小于0.2时，我们称此类海洋结构物为“小构件”，小构件在海水中受力情况通常利用莫里森方程来计算[1]，莫里森方程的微分形式如式(1)。影响莫里森方程计算结果的一个主要因素是方程中惯性力系数和阻力系数的取值，针对小构件圆柱体而言，对于惯性力系数和阻力系数的取值，通常做法是根据表1波浪力载荷计算方法指南来取值。这种取值方式虽然将取值过程简单化，但是该表系数取值的前提条件较多，取得系数值浮动性较大，很容易导致最后计算误差较大。

目前，针对惯性力系数与阻力系数取值的相关研究很多，比较典型的有Brown和Lawler[2](见式(2))，以及通过各种数学和实验方法对此公式具体系数进一步改进[3-4]。Pilyguin等[5]研究了雷诺数在4×105～1×106范围内，流体不同流速对惯性力系数取值的影响。Koji Otsuka等[6]在分析垂直圆柱体在低邱卡数下惯性力受力情况时，得到惯性力系数与邱卡数的大致函数关系如式(3)。大部分的研究主要通过归纳试验结果并对结果进行数学推算，由于研究的针对性，很少将邱卡数和雷诺数同时列入考虑。本文考虑利用数学软件对原始试验与经验数据进行曲线拟合，得到圆柱体惯性力系数和阻力系数随雷诺数和邱卡数变化曲线的函数。

dF=CmρdVu·n+CdρdAu0u0， (1)

1 离散点组采集和曲线拟合

1.1 离散点组采集

所谓拟合是指平面上离散点组所表示的坐标之间的函数关系的一种数据处理方法。从试验与经验中得到若干离散函数值{f1,f2,…,fn}，以这些给定的数据点为基础，通过调整该函数中若干待定系数，确定满足特定要求的函数曲线，并使该函数与已知点集的差别尽量小，称之为曲线拟合[7]。

本文根据试验与经验数据[8]，以雷诺数Re为笛卡儿平面上X轴，以惯性力系数(Cm)为Y轴，由于篇幅原因此处以邱卡数等于40时，圆柱体的惯性力系数随雷诺数变化为例，初步采集X和Y的离散点数据如下：Y=[1.02 1.05 1.1 1.16 1.25 1.37 1.42 1.45 1.5 1.55 1.6 1.69 1.77 1.81 1.82 1.81 1.78]；X=[0.15 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.25 1.5 2 2.5 2.75 3 4]。初步采集的离散点组可能拥有较大误差，因此必须进行修正。将初步采集的数据输入Matlab，生成曲线图象比对试验与经验数据图象，对个别离散点值进行尽量接近试验与经验数据图象的数据修正，得到的结果如下：Y=[1.02 1.05 1.1 1.16 1.26 1.33 1.41 1.45 1.5 1.55 1.6 1.69 1.77 1.81 1.82 1.81 1.78]；X=[0.15 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 1.25 1.5 2 2.5 2.75 3 4]。这里需要说明的是，进行最终拟合的离散点组并不需要完全符合试验与经验数据有2个主要原因：1)由于试验与经验数据也并非精确值，修正过的离散点数据误差很小，因此足以用于实践计算；2)曲线拟合的最终结果函数也并不会准确经过所有离散点组，因此过于精确的数据对于最终的拟合结果意义不大。

1.2 曲线拟合的基本原理

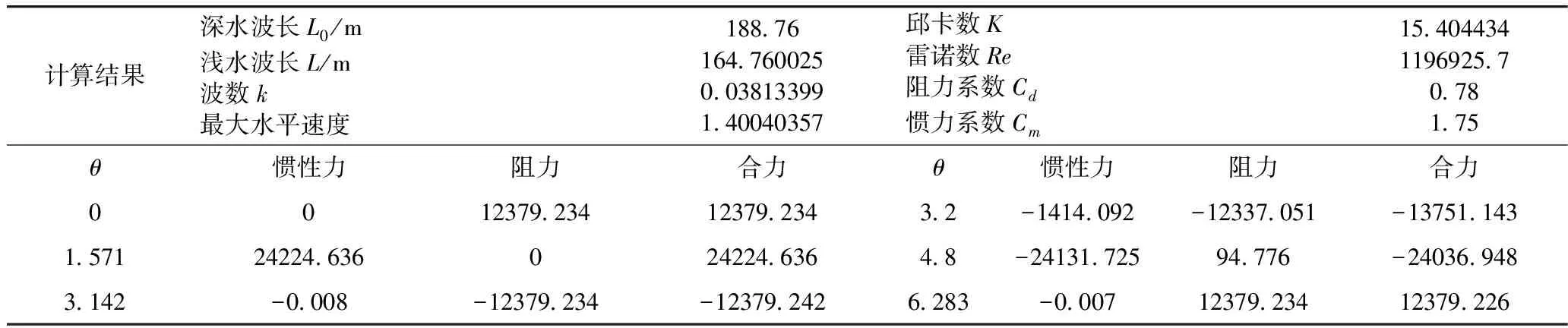
在现实的物理研究过程中，常常需要得到多个测量数据变量的函数关系，此时通常使用一元曲线拟合方法，将实验或经验数据结合数学方法得到多个物理量之间的近似函数表达式。多数情况下，选择曲线使得数据点的平方误差和最小。这种选择就是最小二乘曲线拟合，即曲线拟合最常用的方法，其基本思路如式(4)，其中ki(x)是事先选定的一组函数；ai为待定系数(i=0,1,2…m,m

(4)

1.3 运用Matlab进行曲线拟合

1.3.1 曲线拟合工具Cftool简介

Cftool是Matlab7.0内置的曲线拟合工具箱，拥有可视化的图形界面和强大的图形拟合功能，包括：1)可视化地展开一个或多个数据集，并可用散点图来表示；2)用残差和置信区间可视化地估计拟合结果的好坏；3)通过其他界面可以实现许多附加功能：输出、察看和平滑数据，拟合数据、比较拟合曲线和数据集，从拟合曲线中排除特殊的数据点，选定区间后可以显示拟合曲线和数据集，还可以对数据进行内插法、外推法、微分或积分拟合[9]。Cftool提供的拟合类型有：指数逼近、傅立叶逼近、高斯逼近、插值逼近、多项式逼近、正弦曲线逼近、幂逼近等，适合于各种复杂模型的曲线拟合。

1.3.2 曲线拟合具体操作

由于篇幅问题，无法对圆柱体的惯性力系数和阻力系数随雷诺数和邱卡数变化曲线的拟合过程在文中全部展现，现仍以邱卡数等于40时，圆柱体的惯性力系数随雷诺数变化为例，在Matlab中可以直接通过Cftool命令调用曲线拟合工具箱，对其进行曲线拟合。

在Matlab主窗口输入修正后离散点数据，运用Cftool(X,Y)命令设置拟合数据坐标系，并打开拟合工具箱，单击“Fitting”进行数据拟合设置。分别设置拟合多项式次数为3次、4次、5次和6次，具体拟合效果如图1所示。由图1可以得到5次多项式拟合时，曲线起伏较小且贴近离散点组，同时也符合试验与经验数据图象，拟合效果最好。此处需要说明的是：由图1可得，此例中当雷诺数大于4×105时，惯性力系数发生的变化可以忽略不计，因此不加入Cftool拟合中。以此类推，重复数据采集和曲线拟合的操作，可以得到圆柱体惯性力系数和阻力系数随雷诺数和邱卡数变化曲线的所有拟合结果。

图1 离散点组不同多项式次数拟合结果对比Fig.1 The discrete point group fitting comparison result with different degrees of polynomial

1.3.3 拟合效果评价

对于拟合的效果评价，通常使用2种指标：负相关系数与均方根误差。前文例子中Matlab给出拟合评价指标如下：SSE(误差平方和):0.003 922；R-square(复相关系数或复测定系数):0.997；Adjusted R-square(调整自由度复相关系数):0.995 6；RMSE(均方根误差):0.018 88。可以看出，SSE和RMSE指标比较小，且R-square接近于1 ，说明拟合效果较好，具有使用价值。

1.4 拟合成果的执行程序编写

得到曲线拟合的结果之后，由于得到的拟合函数和相关数据较为繁多，需要一个简单的可视化执行程序，以便在进行相关计算时，能够准确快速地得到惯性力系数和阻力系数。本文运用Visual Basic 6.0将拟合结果编写为一个exe执行程序，具体编写思路如下：首先建立若干控件，包括：用于输入雷诺数的文本框(编写相应代码，确保用户输入数据的正确性，减少程序运行出错几率)；用于选择邱卡数值得下拉列表框；用于开启执行程序的命令按钮；用于显示拟合得到的惯性力和阻力系数结果以及其他说明的标签若干。执行程序的核心代码是拟合函数编写与调用，仍然以前文拟合结果为例，定义拟合结果函数f40代码如下：

Private Sub f40()

x=Text1; If x>4 Then Label1=1.77; ElseIf x>=0.15 And x<=4 Then Const p1=-0.004975

……

Const p6=0.8759; Label1=p1*x^5+p2*x^4+p3*x^3+p4*x^2+p5*x+p6

Else Label1= "无相应数据";End If;If x>4 Then Label2=0.6

ElseIf x>=0.19 And x<=4 Then Const q1=0.01435

……

Const q8=1.583; Label2=q1*x^7+q2*x^6+q3*x^5+q4*x^4+q5*x^3+q6*x^2+q7*x+q8; Else Label2="无相应数据"; End If; End Sub

选择邱卡数后，调用对应拟合函数的代码如下：

Private Sub Command1_Click()

If Combo1.Text="6" Then Call f6; ElseIf Combo1.Text="8" Then Call f8

……

ElseIf Combo1.Text="100" Then Call f100; End If; End Sub。

2 算 例

通过一个算例来验证曲线拟合结果的实际意义。假设线性波理论适用，一个固定导管架平台在30 m水深海域，该处波浪周期为11 s，此结构物主要桩腿是垂直于海水的圆柱钢管，直径1 m。试计算单个桩腿在1个波浪周期内的阻力、惯性力和合力的变化。

传统算法计算结果如表2所示，其中惯性力系数和阻力系数根据表1来取值。惯性力系数和阻力系数按照曲线拟合结果根据具体邱卡数和雷诺数得到的计算结果如表3所示，其中邱卡数取近似值15。

表2 系数查表计算圆柱体波浪周期内阻力、惯性力和合力的变化

表3 系数拟合取值计算圆柱体波浪周期内阻力、惯性力和合力的变化

比对计算结果，由于2个重要系数取值的差异，最终计算结果也产生一定差异。圆柱体受到的最大惯性力和最大合力，拟合取值算法结果比查表取值算法减少了2.78%，误差小于5%在可接受范围内。然而圆柱体所受最大阻力，拟合取值算法结果比查表取值算法增加25.81%，误差大于5%。根据拟合结果得到惯性力系数和阻力系数相比查表取值更接近现实，得出的计算结果更具实践指导意义。

3 结 语

莫里森方程在海洋工程领域应用广泛，方程中惯性力系数和阻力系数的取值直接影响最终工程计算结果。因此惯性力系数和阻力系数越精确，理论模型的计算结果就越具有实践意义。本文利用Matlab软件的Cftool拟合工具箱，对圆柱体惯性力系数和阻力系数随雷诺数和邱卡数变化的试验与经验数据进行拟合，再编写成相应的执行程序(具体编写代码略)，能够方便快速地得到较为准确的惯性力系数和阻力系数。通过一个简单算例证明，拟合结果得到惯性力系数和阻力系数相比查表取值更接近实际情况，因此拟合有较强的实际意义。本文曲线拟合使用的是多项式拟合的方式，同时由于惯性力系数和阻力系数准确取值需要考虑的因素很多，拟合结果取值的精确性还有待提高。

[1] RANDALL R E.Elements of ocean engineering[M].上海交通大学出版社,2002.

[2] BROWN P P,LAWLER D F.Sphere drag and setting velocity revisited[J], Journal of Environmental Engineering-ASCE,2003(3)：222-231.

[3] CLIF R,GRACE J R,WEBER M E.Bubbles,drops,and particles[M].Academic Press,New York,1978.

[4] TURTON R,LEVENSPIEL O.A short note on the drag correlation for spheres[J].Powder Technology,1986,47(1):83-86.

[5] PILYUGIN N N,KHLEBNIKOV V S.Investigation of aer-odynamic drag of two bodies in trans- and supersonic flows[J].Journal of Applied Mechanics and Technical Physics,2003,44(2):187-192.

[6] KOJI O,YOSHIHO I.Estimation of inertia forces on a horizontal circular cylinder in regular and irregular waves at low Keulegan-Carpenter numbers[J].Applied Ocean Research,1996,18:145-156.

[7] 樊晓红.样条函数与基于样条函数的数据拟合方法[J].科技信息,2011(9)：507-508.

[8] SARPKAYA,ISAACSON.Mechanics of wave forces on offshore structures[J]，New York:Van Nostrand Reinhold Co.,1981.

[9] 苏金明,张莲花,刘波,等.Matlab工具箱应用[M].北京:电子工业出版社,2004:489-512.

[10] 伦冠德.MATLAB曲线拟合工具箱在试验数据处理上的应用[J].拖拉机与农用运输车,2006(8)：90-91.