谨慎对待数学学习中的“非思考”现象

陈士策

(扬州市沙口小学，江苏扬州，225003)

小学数学课程标准明确提出：“要求学生能够体会数学知识之间、数学与其他学科之间、数学与生活之间的联系，运用数学的思维方式进行思考，增强发现问题和提出问题的能力、分析问题和解决问题的能力。”这要求学生在数学学习中一定要充分发挥自己的数学思维，进行独立、深入的数学思考。但是在实际教学中，我们往往会看到这样的现象：学生解决了有些数学问题，其实并没有真正理解;学生看似思考了，其实只是停留在问题的表面，并没有深入……究其原因，可能是教师在教学中对某一具体问题的解决看得过重，而忽视了给学生独立思考的机会。学生的数学学习已经成为非主动学习，他们千方百计地解决问题只是为了完成任务，只是为了解答某一道题目。在此过程中，他们对问题的思考其实并没有深入，并没有在解决实际问题的过程中真正发展自己的思考能力，并没有表达自己真实的思考和想法。因此，学生并没有学会独立思考，在解答问题的过程中的所谓思考其实是一种“非思考”状态。在教学中，教师如果只满足于学生答对问题、能够解决问题，而对学生的思维不进行深入分析，那么学生的数学学习就很难得到真正提高。

一、猜测

我们在教学“长方体和正方体”一节时，认识了体积和容积之后，教材中有这样一道巩固习题：

试一试：下面哪个玻璃杯的容积大一些，你能想办法比一比吗?(如图1)

图1

教学片段：

师：谁来说说怎样比较呢?

生1：右边的杯子容积大。

生2：不对，左边的杯子高一些，左边的容积大。

学生在课堂中争辩着……

在他们争执不下的时候，教师提出了问题：“你们怎样才能证明自己的答案是正确的呢?”很快有学生提出了自己的想法：“老师，可以找两个杯子来倒水，做个实验就知道谁的容积大了。”为了使教学顺畅，教师顺势拿出了课前准备的两个杯子，并根据学生提出的方法进行了实验：将右边那个矮一点、粗一点的杯子盛了满满一杯水，然后很小心地往左边那个高一点、细一点的杯子里倒。实验结果是左边的杯子水已倒满，右边的杯子里还有一点儿水，这证明了右边杯子的容积稍大一些。“耶!”猜对的学生欢呼起来，猜错的学生则垂下了头。

这样的教学，学生看似思考了，但其实是一种“伪思考”，他们的思考只是停留在“两个杯子哪个容积大”这一具体问题上面。在实验过程中，他们关心的是答案，而没有去体验思考过程的快乐，没有对所有可能的情况进行全面细致的思考和分析。找出比较的方法固然重要，但是在操作之前对可能出现的情况进行分析更为重要，这才是真正的思考。当学生提出倒水的方法之后，教师应该做的不是立即进行实验，而应让学生思考：倒水会出现什么情况，每种情况出现后说明了什么问题。即时的实验只是验证学生猜测的结果，而没有让学生真正体会实验的本真意义。

二、排除

有一些数学问题的解答可以通过直接的数学思考解决，也可以通过其他方式解决，比如排除法。当问题解决存在多个可能性选项的时候，有一种办法是将各种错误选项排除，最后就剩下正确的选项。在平时的学习中，这能够帮助学生解答某一道题，但是很难说学生对数学知识理解深刻，他们的思考其实并不到位。

例如：在苏教版六年级上册补充习题第5页中有这样一道题目：

在○里填上“＞”“＜”或“=”。

1．当 x=2 时，3．2x+1．5x○10

2．当 y=4 时，8y－3y○20

3．当 x=0．7 时，0．4x+0．6x○0．5

4．当 x=1．1 时，1．1x －0．4x○0．77

这道题需要学生根据方程的意义把未知数的值代入左边进行计算，然后比较左右两边数式得出结论。但实际作业时，可能是因对方程的理解不到位，也可能是学习态度不端正或是小数计算不过关，许多学生会在第2、第4两题出错，他们会在“○”填上“＞”或“＜”。这时，教师如果把自己认真批改之后的作业及时发下去让学生订正，细心观察就会发现，作业出错的学生中有相当一部分把错题一看，不假思索地就把原来的答案由“＞”改成“＜”(或者由“＜”改成“＞”)，然后就信心满满地将作业拿给教师批改……这样至多订正到第二次，正确答案就会出现。“可能性”只有三种，排除了前两种，正确的只能是第三种。学生在解决问题的过程中其实根本没有真正地进行数学思考。

当遇到这种情况时，教师不能急于求成，可以将作业暂时放置一旁，将类似的习题呈现并在全班进行分析，让学生理解应如何去思考，而不是简单地应付式完成作业、找到答案。这样搁置一段时间后，教师再找合适的机会将错题以新题的形式呈现在黑板上，让学生独立思考、完成，并最终完成解答。这能够最大限度地抑制学生的思维惰性，防止他们应付式地解答问题，从而真正促进学生主动地思考、解决问题。

三、模仿

教材中的例题都是精心挑选、便于学生学习思考的典型题目。在教学中学生通过对例题的思考进而掌握数学知识。可是在实际教学中，为了追求正确率，部分教师会教给学生一些所谓的“高招”来提高作业正确率。比如教师经验式地让学生根据例题进行简单模仿，这样学生完成作业的效率会很高，但是未必能够真正理解所学的内容，过于注重模仿也就失去了深入思考数学问题的机会。

片段：列方程解决实际问题第1课时。

师(出示例题)：题目中告诉我们哪些信息?要我们解决什么问题?

生1：大雁塔高64米。

生2：比小雁塔高度的2倍少22米。

生3：求小雁塔高多少米?

师(启发)：你能从中找出它们高度之间的关系吗?题中的哪句话能清楚地表明它们之间高度的关系?

生：比小雁塔高度的2倍少22米。

师：对，根据这个条件，我们可以知道用“小雁塔的高度×2－22=大雁塔的高度”，现在我们就可以根据这个关系列方程来解答。

……

随后，学生进行巩固练习时，教师提出了这样的问题：“刚才我们是根据‘小雁塔的高度×2—22=大雁塔的高度’这一关系列方程的，现在你试一试找出哪个条件相当于例题中的大雁塔，哪个条件又相当于小雁塔呢?这里的‘少’又怎么处理呢?”根据教师的提示，学生很快完成作业，并且正确率非常高，他们根据“青马大桥长度×18+0．8=杭州湾大桥长度”这一关系来列方程。课后，笔者查看了学生的书本，有一半以上的学生都在“青马大桥”下写了一个“小雁塔”，“杭州湾大小桥”下写了一个“大雁塔”，在“少”后面写了一个“－”。

不可否认，教师的暗示还是起到一定作用，许多学生立即正确“找到”了方程中数量之间的相等关系并能正确解答，但是这样的提示有效吗?这样的思考又有什么作用呢?学生的思考其实是一种简单、低级的模仿，只是为了解决问题而模仿。数学的教学绝对不是为了顺利解答某一道题目而教，应该为学生独立、有主见地进行数学思考而努力。因此，教师在教学中必须注重孩子自己对数学问题本真的理解，促进他们积极主动的数学思考。

四、记录

在教学中，有些实际问题比较难理解，并不是所有学生都能够立即理解。教师的教学必须建立在学生真正理解、掌握分析和解决问题的方法的基础上，而不能在仅有极少数学生理解时就急于把解题思路呈现，这样部分学生就可能凭记忆来解决问题。

例如笔者在教学六年级上册第一单元第8页的思考题时，就出现这样的情况。题目是：“盒子里有同样数量的红球和白球，每次取出6只红球和4只白球，取了若干次以后，红球正好取完，白球还有10个。一共取了几次?盒子里原来有红球多少个?”这是例题教学完之后的一道思考题，其难度虽然有提高，但仍能完全放手给学生，让学生通过自己的思考先尝试。但是一些教师在教学过程中过于注重教学的结果，教学中直接指出题中关键进行引导，很快在优等生的帮助下就在全班建立了解题思路：“设一共取了x次，因为两种球原来同样多，用取的红球个数减去取的白球个数就得到10。”许多学生会在此提示下及时在书上把数量关系甚至所列方程记录下来，这样他们做作业时完成的质量很高。但是过了一段时间，当再次用同类型题目给学生解答时，发现有相当一部分的学生仍然不会。其实细细思考就会发现：这部分学生当初的作业做对并不是建立在理解的基础上，他们可能根据教师的提示而直接在书本上记录下了思路、方程，将思考题转化为计算题，其难度要小许多，解答正确也就不奇怪了。所以教师无论给什么样的提示都必须以学生的思考为中心，这样才能最大限度地提高教学效率，才能真正有效地促进学生数学思维的提升。

五、做对

在教学中，学生可能用一些简单但不够严密的方式进行思考、解答某些问题，答案也能恰好正确。这时如果教师在教学中满足于学生对问题的完成、做对，而对题目不进行深入的变化，促进学生深入的思考，那么对于某一道题目学生的答案可能是对的，但学生的数学思考并没有得到完善，他们的思考并不够深入、细致。

笔者在学生作业过程中曾遇到这样的一道题目：“一个纸箱的容积是6000立方厘米，把6盒(如图2)饼干筒装入这个纸箱里，能装下吗?”多数学生的解答是：9．5×6×19=1083立方厘米;1083×6=6498立方厘米。因为：6498立方厘米＞6000立方厘米，所以不能装下。

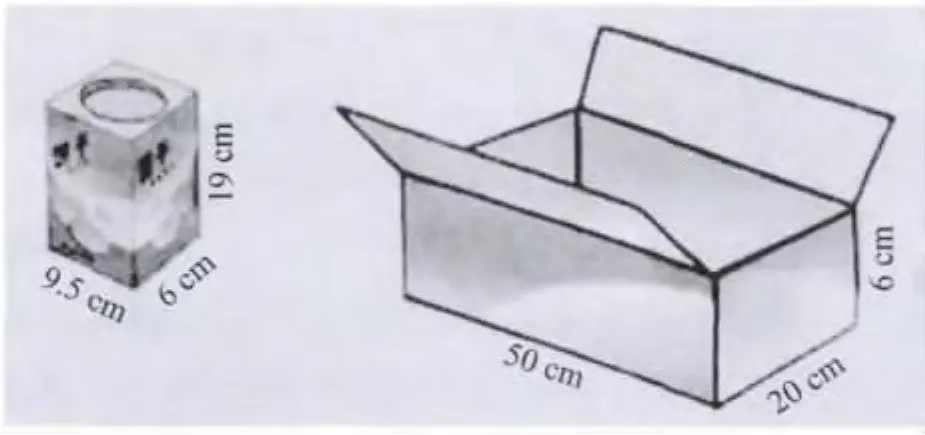
图2

从答案上看，这样做是正确的，但是我们把这个纸盒的高度改为7厘米呢，就能够装下去吗?显然不能。但是按照上面的方法应该是能的。在这里，如果教师只以答案的正确与否评定学生而没有关注学生的思考过程，那么对学生的数学思考是无效的甚至会起负作用。教师对学生的作业既要关注结果，更要关注学生的思考过程。只有当学生对问题进行了深入、完善的思考，他们的解答才值得肯定的。教师在教学中不能简单以答案正确为评价标准。

培养学生的数学思考能力不是一朝一夕的，教师在教学中必须让学生真正进行独立的数学思考，对每一个问题、每一个知识点的理解都应该是学生自己进行的，不能以点带面，以偏概全。在任何时候教师都要把学生自主学习的能力发展放在第一位，要充分发现、培养学生独创性思维，要注意学生数学学习能力的提升。

［1］ 楚长锦．教会学生举一反三——对数学学习“懂而不会”现象的思考［J］．新课程研究：中旬，2013(4)．

［2］ 万映红．如何对待小学生数学学习中的错误［J］．小学教学参考，2008(24)．