大规模风电接入对电力系统暂态稳定性影响机理研究

汤 蕾，沈 沉

（清华大学 电机系，北京 100084）

随着风电技术逐步成熟，风电并网规模不断增大，风电场接入对电力系统的影响越来越显著，电力系统在电压稳定、频率稳定、电能质量、次同步振荡等方面都呈现出更为复杂的特性［1-6］，电力系统的安全稳定运行面临新的挑战，其中，大规模风电接入下电力系统的暂态稳定性也是人们关心的热点问题之一。

目前，双馈发电机（Doubly Fed Induction Generator，DFIG）已成为风电场的主流机型。双馈风机的暂态特性明显区别于传统同步机组（Synchronous Generator，SG），同时，大型风电场的并网改变了电网中的潮流分布，从而影响常规机组的同步转矩，因此，有必要探究含大量双馈风机的电网暂态稳定机理。

大量文献对风力发电机的暂态行为开展了深入研究，在此基础上制定风电机组的低电压穿越控制策略［7-10］。现阶段不少学者开始将研究重心转移到大型风电场与电力系统在暂态稳定方面的相互作用上，大多数研究采用定性分析和仿真验证相结合的方法开展，例如：文献［11］在DFIG功角定义的基础上讨论了双馈风机和同步机并列运行时的相互作用，将2种机组受扰功角轨迹的交点分为主动交越和被动交越点。在主动交越点处，SG功角振幅随DFIG功角增大而增长，不利于暂态稳定性；被动交越点的性质则正好相反。仿真表明，大扰动下同步机第1摆出现主动交越点，DFIG的接入降低了第1摆暂态稳定性，在后续过程中，出现被动交越点，增强了阻尼作用。文献［12］认为当有功潮流变化不大时，DFIG能否向系统提供无功支撑对同步机组功角稳定性至关重要。可以利用DFIG无功控制的特性，减轻同步机组的无功负担，减小系统中的电压跌落，从而维持电磁功率与机械功率的平衡，提高系统的功角稳定性。文献［13］的研究结果表明，如果双馈风机具有良好的低电压穿越能力，在接入弱电网时就不会对系统的暂态稳定性产生负面影响。

由于仿真模型和算例不同，上述文献通过时域仿真得出的结论不尽相同，因此，也有少数学者尝试通过定量分析寻求大量风电接入对电力系统暂态稳定性的影响机理。文献［14］将风电场的注入电流等值为临界群内节点的接地导纳，进一步将双机系统等效为单机无穷大系统，把风电注入对系统不平衡功率的贡献近似为双机模型中临界群的机械功率变化量，结合理论推导和扩展等面积定则得出结论，如果风电机组变速范围较宽，在故障期间以及故障切除后的一段时间仍然能够参与暂态控制，那么在第1摆正向摆动时一般能够减少加速能量，增加减速能量，有利于系统暂态稳定。

笔者首先从双馈风机的暂态特性出发，分析在故障切除后暂态过程中将双馈风机视为恒功率源的可行性和限制条件，再将大规模风电接入后系统的发电和负荷平衡情况分为2种情形：①通过减少同步机出力来平衡新增风电；②停运部分同步机组平衡风电。进而在上述场景下，基于直流潮流模型和等面积定则，定性分析大量风电接入简单电力系统中的暂态稳定机理，并通过仿真验证该暂态稳定机理的正确性。

1 暂态稳定分析元件模型

文献［15-17］考虑了电力系统中各元件仿真模型对含风电电力系统的暂态稳定研究结果的影响，其中，文献［16］考虑了经典2，4，6阶模型3种同步发电机模型。仿真结果显示，无论采用何种同步发电机模型，都不影响含风电系统暂态稳定分析的结果。因此，该文的机理分析将采用同步发电机的经典二阶模型。

文献［17］讨论了研究暂态稳定问题对风机及其控制的建模要求，并得出结论：对于双馈风机，暂态稳定分析时无需考虑风力随机性的影响；小型风电场可以等效为一台机，大型风电场可以根据风力输入“分群”，等效为几台机组。该文的重点是从功角稳定角度考察双馈风机和同步发电机动力学特性的相互作用，因此，笔者不考虑风速不确定的影响，并将风电场等效为多台2MW双馈机组进行分析。

双馈风机动力学特性复杂，在进行暂态稳定机理分析时如何简化双馈风机模型值得思考。当双馈风机转子侧变换器采用定子电压矢量控制时，同步速旋转坐标系d轴方向与定子电压矢量Us方向相同，双馈风机输出有功功率表达式为［18］

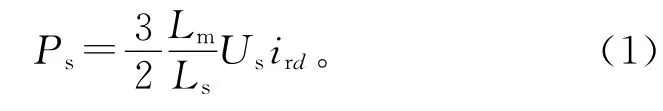
式中 Lm为双馈风机定转子间互感；Ls为定子电感；Us为定子电压大小；ird为转子电流d轴分量。

在定子电压矢量控制方式下，功率控制外环根据有功、无功控制目标给定转子d，q轴电流的参考值，电流控制内环根据外环输出的参考值校正转子电流的d和q轴分量，控制变量分别为转子电压的d和q轴分量。ird的控制方程［18］为

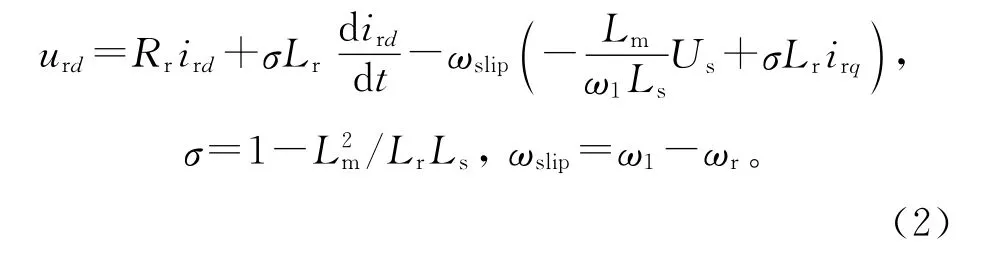
式中 Rr，Lr分别为转子电阻和电感；ω1为同步转速；ωr为转子转速。由此可得ird的动态过程时间常数为

根据文献［19］，外环和内环的PI控制环节时间常数均在10ms左右，ird的动态过程时间常数在100ms级别，因此，ird的控制时延仅为100多ms。在稳态情况下，双馈风机能够实现恒功率控制，快速跟踪设定的有功和无功功率，因此，在不考虑风电不确定性时，可以将故障发生前的双馈风机等效为恒功率源。在故障发生到故障清除时间段内，双馈风机定子电压跌落，无法实现准确的功率控制，此时双馈风机的输出功率由其本身的动力学特性以及低电压穿越策略决定。

故障清除后，双馈风机输出功率的恢复速度取决于ird的控制时延和Us的恢复速度。如果双馈风机具有良好的低电压穿越性能，在故障切除后Us恢复到正常水平，双馈风机就能相应恢复到恒功率状态。文献［17］指出故障清除后双馈风机电压恢复较快；文献［20］的研究表明DFIG转子运动不存在机电暂态失稳问题，并且功率具有快速恢复特性，恢复时间不到1s。同步发电机暂态稳定时间尺度通常是扰动后3～5s，对具有明显的区间振荡模式的大型电力系统可将时间尺度延长到扰动后10～20s［21］，因此，相比于同步发电机，当双馈风机具有较强的低电压穿越能力时，在故障切除后的暂态过程中可以将双馈风机视作恒功率源。

2 简单电力系统说明

笔者将从单台同步发电机接入无穷大系统入手，从理论上推导大规模风电接入条件下系统的暂态稳定机理，再将该机理推广到双机系统乃至多机系统中。考虑单机无穷大系统接入双馈风机时，将同步发电机收缩到內电势节点，在故障发生前和故障清除后双馈风机等效为恒功率源，考察系统潮流分布的改变对同步发电机功率—功角曲线的影响。

大规模风电接入后，系统中的发电量大于负荷量，实现功率平衡的思路一般有2种：①减小同步发电机的出力；②停运部分同步机组。采取部分同步机减小出力的方法仅仅改变了系统潮流分布，系统惯量不会发生改变，而同步机停机会导致潮流分布和系统惯量都随之改变。

为了叙述方便，该文以及附录中涉及到的变量符号含义汇总如表1所示。

表1 变量符号说明Table 1 Notations description

3 暂态稳定机理分析

3.1 暂态稳定机理分析方法

同步发电机采用经典二阶模型，考虑三相短路故障，故障期间Pe=0，在单机无穷大系统中同步机角速度和功角满足：

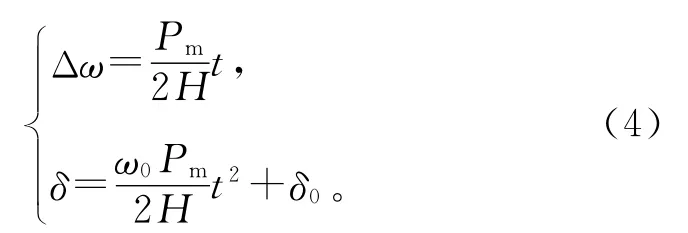
设风电接入前、后同步发电机功角变化值为Δδ=δ′-δ，则该变量衡量了大量DFIG接入对同步发电机功角稳定性的影响，功角差Δδ的二阶导数满足：

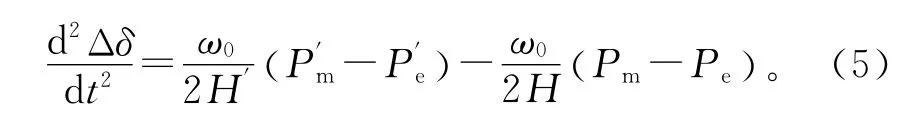
在单机无穷大系统中，故障期间，Pacc=Pm，一般为正数；故障清除后，Pdea=Pm-Pe，一般为负数。因此，在故障期间，式（5）等号右边的表达式衡量了加速面积变化量；在故障清除后，该表达式的相反数表示减速面积变化量。只要求出故障期间以及故障清除后的Pm和Pe，便可以估计出风电接入前后加速面积和减速面积的变化趋势，进而分析风电接入对同步机功角的影响。

为了直观地理解暂态稳定机理，笔者采用直流潮流分析风电功率注入引起的系统潮流变化，进而计算Pm和Pe，虽然在大扰动情况下直流潮流的计算误差较大，但潮流分布改变的趋势是正确的。

3.2 同步机减小出力

采取部分同步机减小出力的方法，系统惯量不会发生改变，H′=H。

在直流潮流模型中，将无穷大母线视为平衡节点，则同步发电机的稳态功角为

故障期间Pe=0，满足：

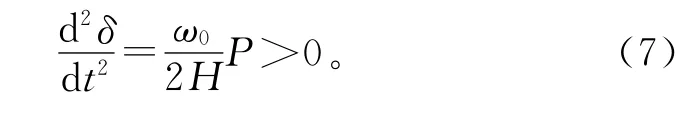
故障清除后，基于直流潮流模型，同步机功率—功角关系Pe-δ可以记作：

由于同步机到无穷大母线之间的电气距离相应变为xII，此时有

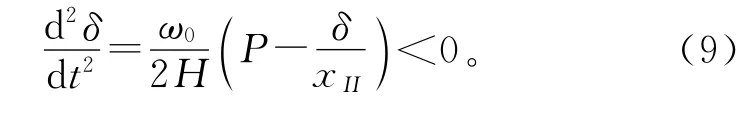
风电接入后同步机出力减小，双馈风机出力和同步机出力分别满足：

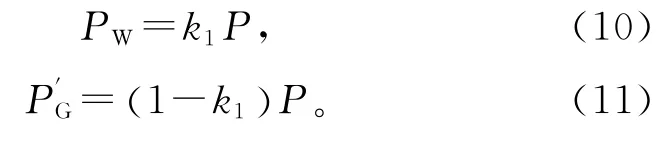
如图1所示，在直流潮流模型中，节点功率注入与节点电压相角近似为线性关系，根据叠加定理，风电注入恒定功率导致同步机稳态功角变为

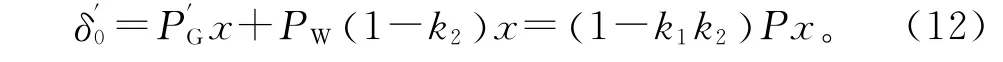
稳态功角变化量为

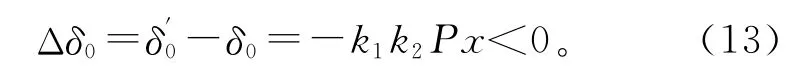
因此，风电接入后若同步机出力减小，则有稳态功角减小，风电接入量越大，接入点距同步机组越远，稳态功角减小得越多。

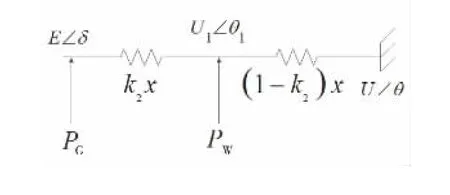
图1 风电接入后同步机出力减小场景Figure 1 Wind power penetration with synchronous generation output reduced scenario

风电接入后，故障期间有

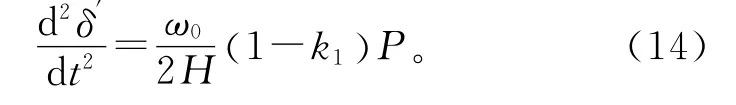
式（14）与式（7）相减有

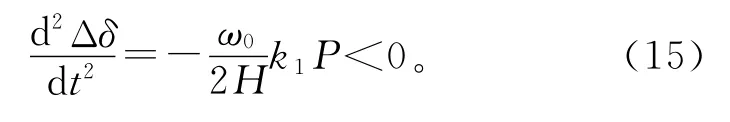
暂态过程中同步电机的电磁功率Pe=PG，由此可得风电接入后同步机的功角关系：

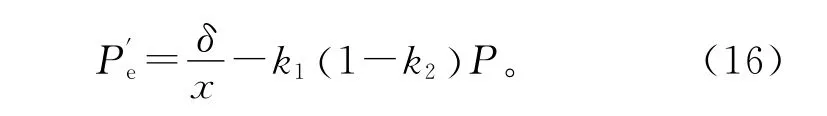
故障清除后，同步机功角满足：

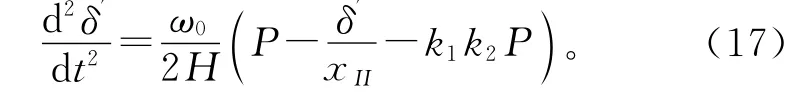
式（17）与式（9）相减有

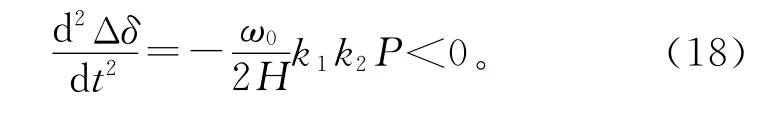
根据式（15）和（18）可知，双馈风机接入后同步机减小出力，会引起同步机功角加速面积减小，减速面积增大，意味着第1摆功角摆幅减小。结合前文的分析，风电接入后稳态功角减小，第1摆功角摆幅减小，可得δcr-δ0增大。进一步考虑极限切除时间tcr的变化，减小同步电机出力，系统惯量大小不变，此时有

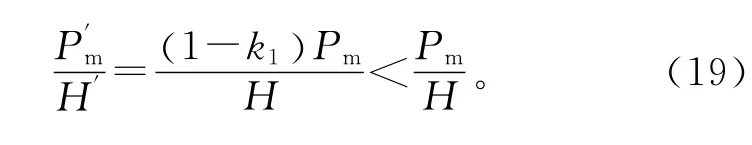
根据式（4），δcr-δ0增大，Pm／H减小，极限切除时间tcr增大。

由此可见，若接入风电后同步机减小出力，则风电接入将对系统暂态稳定性产生正面影响，并且风电替换比例越大，风电接入位置距离同步机越远，越有利于系统暂态稳定性。

3.3 部分同步机停机

假如风电接入后停运部分同步机，与同步机减小出力的场景相比，潮流分布的改变相同，因此，稳态功角变化量仍然满足式（13）。

停运部分同步机后，系统惯量与同步机总出力同比减小：

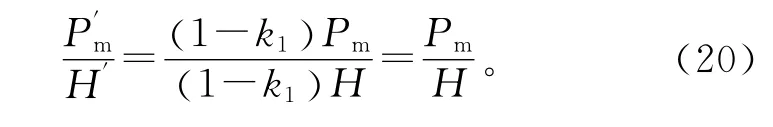
因此，故障期间有

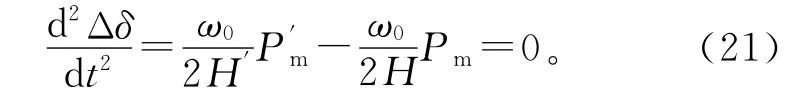
故障清除后有

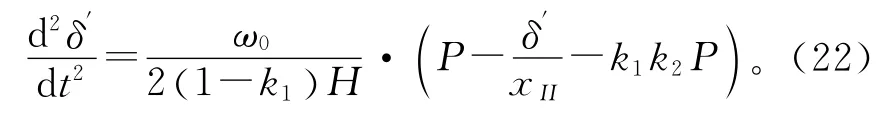
式（22）与式（9）相减有

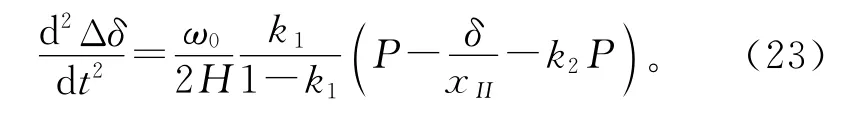
根据式（9）可以判断式（23）右边表达式为负数。

由此可见，当停运部分同步机组时，同步机稳态功角减小，加速面积不变，减速面积增大，因此δcrδ0增大。根据式（4），仍然可以得出极限切除时间tcr增大的结论。

综上所述，通过减小同步机总发电量来实现风电接入后的功率平衡，无论是同步机减小出力，还是停运部分同步机组，都会对系统的暂态稳定性产生正面影响，并且风电接入量越大，风电接入点距离同步机越远，对系统暂态稳定性的影响越好。

3.4 多机系统讨论

暂态稳定机理考虑的是单机无穷大系统，其结论可以用于多机系统的单机暂态失稳模式。双馈风机的接入之所以能够改善单机无穷大系统的暂态稳定性，是因为双馈风机减轻了同步发电机的功率负担，并且由于其本身不存在功角稳定的问题，故障后输出功率能够很快恢复，在同步发电机输出功率恢复的过程中，双馈风机能够向系统提供有功潮流从而维持同步转矩。此外，风电接入点越靠近负荷，越能够减小系统中的功率传输，改善潮流分布，因此更加有利于系统暂态稳定性。

对于双机摇摆模式，等效于研究双机系统接入风电对两同步机功角摆开幅度的影响。事实上，单机无穷大系统可以视为两机系统的极端情况，即受端机组的惯量为无穷大。如果在双机系统中，受端机组惯量远大于送端机组，则可以将其近似视为单机无穷大系统，将单机无穷大系统的有关结论推广可知，此时只要风电接入以及两同步机出力调整不改变潮流流向，即潮流依然是从送端向受端传输，则有风电接入对系统产生正面影响，并且风电接于受端更佳。相反地，如果送端机组惯量远大于受端机组，暂态过程中受端机组的功角加速度大于送端机组，送端机组相对于受端来讲经历了反向加速的过程，因而此时的结论与单机无穷大系统恰好相反，即风电接入会对系统产生负面影响，并且风电接于送端会减轻负面影响。

对于多机系统而言，按照扩展等面积定则，可以判断系统的失稳模式，把受扰严重机组归为临界群，其余机组归为余下群，进一步可以定义临界群和余下群的等值功角、角速度和惯量，将多机系统暂态稳定分析问题转化为两机系统的分析，从而可以运用上述结论判断风电接入后的暂态稳定性。

4 算例分析

4.1 单机无穷大系统

首先双馈风机采用恒功率模型进行仿真，同步发电机采用经典二阶模型。单机无穷大系统接入风机之前，同步机出力为2 000MW，在距离送端30%处设置三相接地短路故障。考虑2种故障清除情况：一段时间后故障消失和一段时间后切除故障线路。设置风机接入前、后同步机惯量不变和惯量减少2类情形，分别对应同步机出力减小和停运部分同步机场景。

将风电接入点固定在同步机到无穷大母线的30%处，改变双馈风机替换同步机的比例，考察其对极限切除时间影响，如表2所示，可以看到，随着风电替换同步机的比例增大，故障的极限切除时间单调增加，符合第3节的理论推导。

将风电替换比例固定为20%，改变风电接入位置，极限切除时间的变化如表3所示，风电接入位置距离同步机越远，极限切除时间越大，与理论推导结果相同。

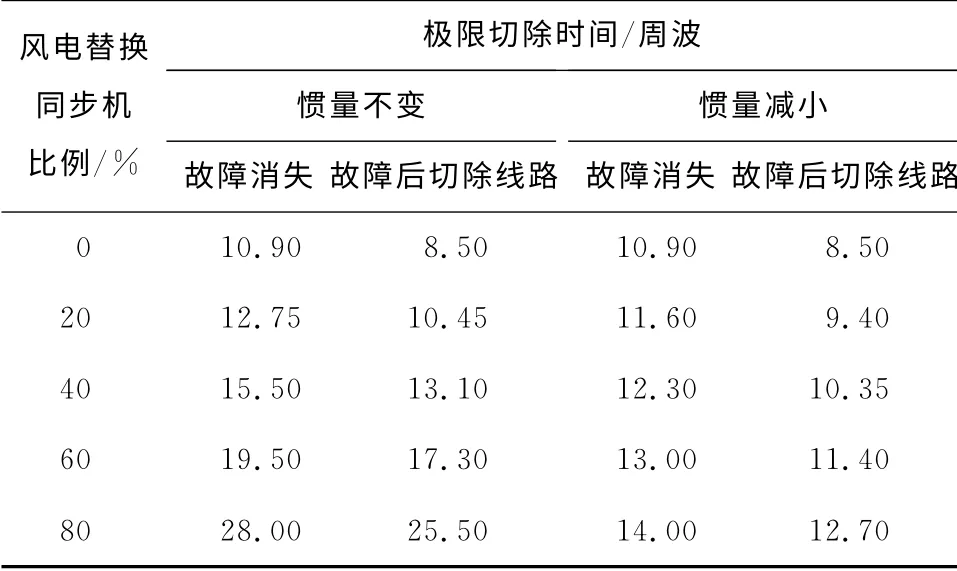
表2 双馈风机视为恒功率源时风电替换比例对极限切除时间的影响Table 2 Influence of wind power penetration on critical clearing time with DFIG viewed as a constant power source

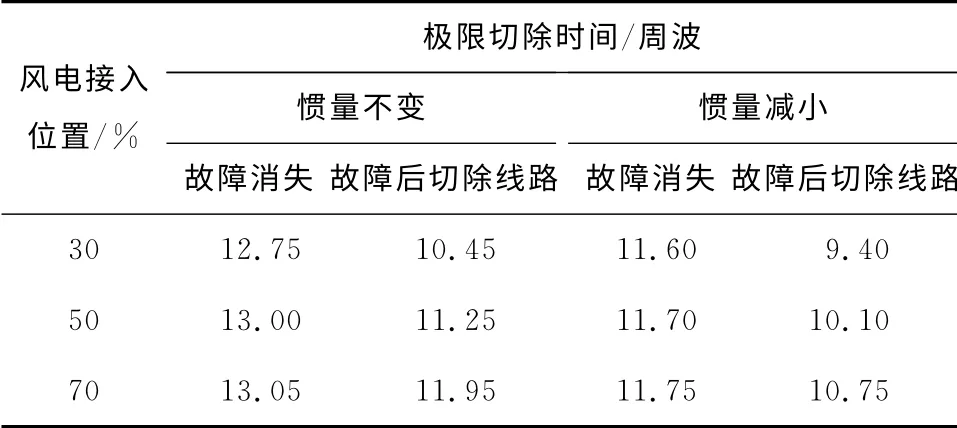
表3 双馈风机视为恒功率源时风电接入位置对极限切除时间的影响Table 3 Influence of wind power access point on critical clearing time with DFIG viewed as a constant power source

上述算例中双馈风机采用恒功率源模型，仿真结果和理论推导完全符合，有必要进一步验证双馈风机采用恒功率模型的可行性。

在DIgSILENT PowerFactory中使用双馈风机详细模型进行仿真，风速视为恒定，模型由异步发电机、风力机控制子系统和转子侧PWM变换器子系统组成。其中，风力机控制子系统包括风力机模块、传动轴模块、最大风功率跟踪模块和桨距角控制模块，转子侧PWM变换器控制子系统采用定子电压定向矢量控制，包含电流控制内环和功率控制外环2个PI控制环，能够实现双馈风机最大风功率跟踪和有功无功解耦控制，此外模型中还设置了Crowbar保护，双馈风机具有低电压穿越能力。

考虑风机接入前同步机出力为1 000MW，三相短路故障时长为6个周波，风电接入点位于同步机到无穷大母线的20%处，改变双馈风机出力，分别使用DFIG详细模型和恒功率源模型进行仿真，观察同步机最大功角的变化。如表4所示，根据汇总的仿真结果可见，与DFIG详细模型相比，采用恒功率模型获得的最大功角偏差不大于1.1%。使用DFIG详细模型得到的风电替换比例对系统暂态稳定性的影响规律仍然与第3节的理论推导吻合。

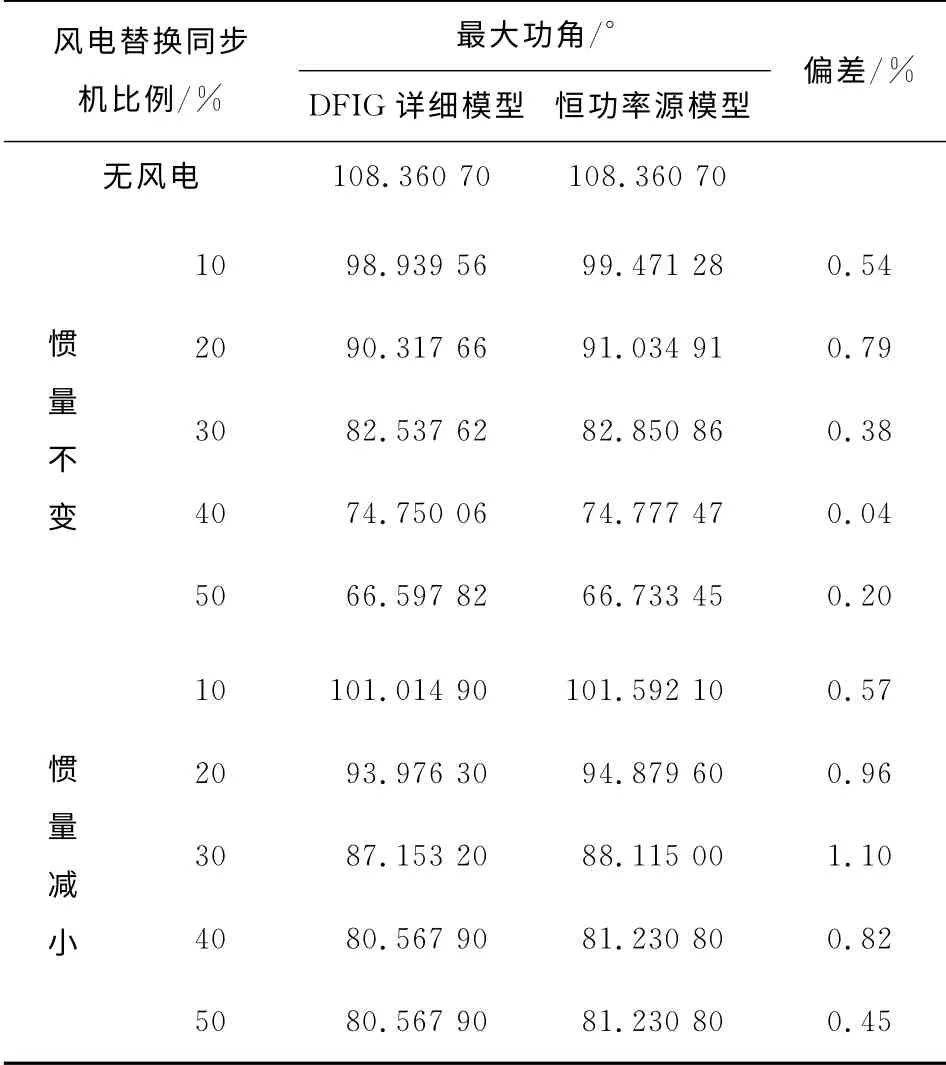
表4 双馈风机采用不同模型时风电替换比例对同步机最大功角的影响Table 4 Influence of wind power penetration on maximum power angle with different DFIG models

风电替换比例设为30%，风电接入位置变化，不同双馈风机模型下的仿真结果如表5所示，可以看到，DFIG详细模型下的仿真结果仍然符合第3节对风电接入位置影响机理的论述。

由此可见，在进行大规模风电接入的电力系统暂态稳定分析时，只要双馈风机具有良好的低电压穿越能力，可以将双馈风机视作恒功率源，简化暂态稳定分析过程。

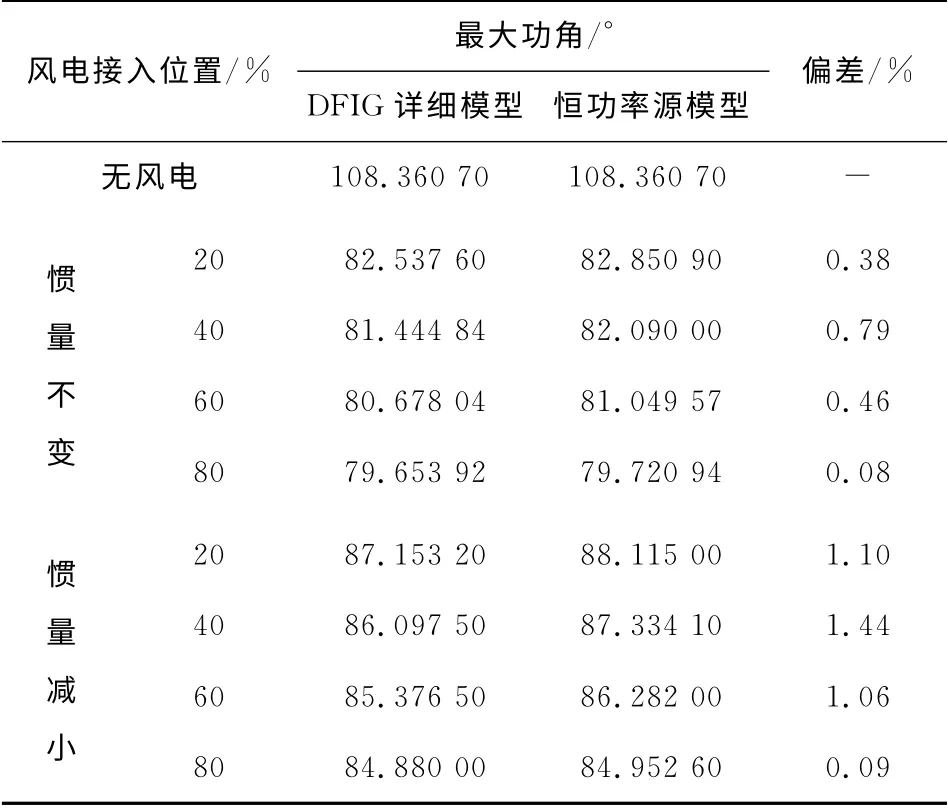
表5 双馈风机采用不同模型时风电接入位置对同步机最大功角的影响Table 5 Influence of wind power access point on maximum power angle with different DFIG models

4.2 双机系统

在DIgSILENT PowerFactory中搭建仿真模型，如图2所示，接入风机前G1出力为900MW，G2出力为600MW，负荷L7为500MW，L9为1 000MW，从区域1到2的联络线潮流约为400MW。

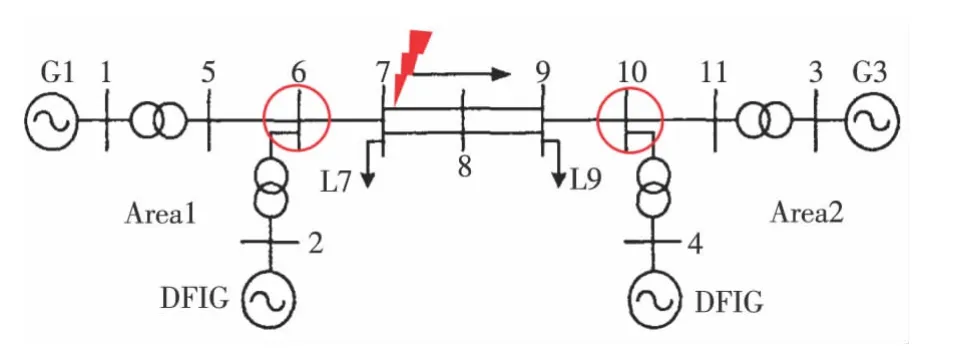
图2 双机系统示意Figure 2 Schematic of double-generator system

设集中接入300MW的风电，即风电替换比例为20%。由于风电接入产生的功率差额80%由送端同步机G1承担，即送端同步机出力减小240MW，受端同步机出力减小60MW。风电接入位置在距离送端40%（节点6）或者60%（节点10）处，双馈风机采用第4.1小节的详细模型。分别考虑送端机组惯量小于受端机组以及受端机组惯量小于送端机组2种情形，送端机组G1占G1，G2总惯量的比例（简称“送端惯量比例”）分别设为30%和70%，三相接地短路故障发生在节点7和8之间双回线的其中一条首端，故障时长为20周波，仿真获得的G1，G2最大功角差如表6所示。

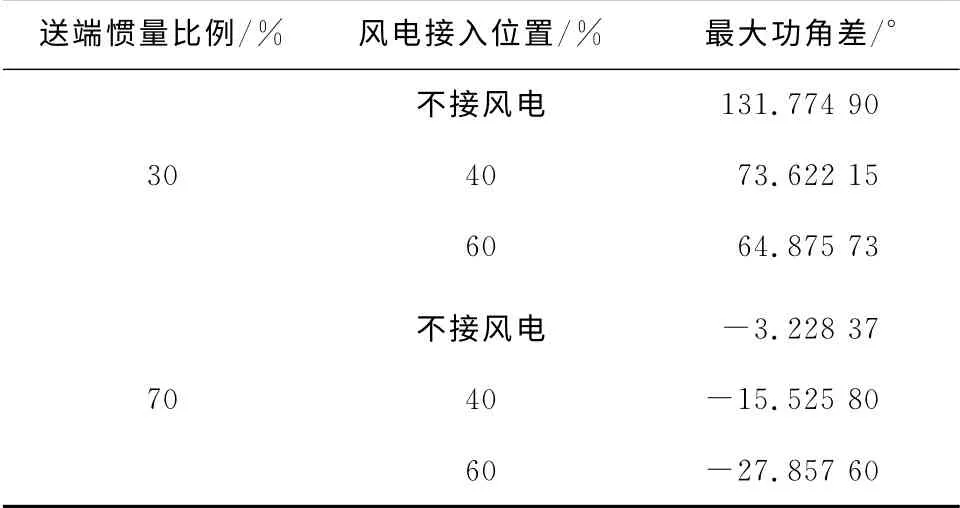
表6 含风电的双机系统最大功角差Table 6 Maximum power angle difference of doublegenerator system with wind power penetration

由表4中数据可见，当送端惯量比例为30%时，送端机组功角加速度大于受端机组，风电接入会改善系统暂态稳定性，并且风电接在受端更为有利；当送端惯量比例为70%时，受端机组功角加速度大于送端机组，风电接入后最大功角差绝对值增大，意味着双机系统的暂态稳定性恶化，当风电接于40%（送端系统）处时，负面影响有所缓解。仿真结果证明了第3.4小节对双机系统暂态稳定机理的讨论结果。

5 结语

笔者从双馈风机的暂态特性出发，基于直流潮流模型和等面积定则，分析大量风电接入简单电力系统中的暂态稳定机理，并通过仿真证明了该暂态稳定机理的正确性。

1）在进行大规模风电接入的电力系统暂态稳定分析时，只要双馈风机具有良好的低电压穿越能力，可以在故障发生前和故障清除后将双馈风机视作恒功率源。

2）在单机无穷大系统中，风电接入后能够改善潮流分布，减轻同步机的功率负担，在故障清除后双馈风机能够贡献有功潮流从而维持同步转矩；风电接入后无论是同步电机减小出力还是停运部分同步机组，都会对系统暂态稳定性产生正面影响，并且替换比例越大，接入点距送端越远，越有利于暂态稳定性。

3）在双机系统中，当受端机组惯量远大于送端机组时，风电接入会对系统产生正面影响，并且风电接于受端更有利；相反地，如果送端机组惯量远大于受端机组，风电接入会对系统产生负面影响，并且风电接于送端会减轻负面影响。

笔者对大规模风电接入下的电力系统暂态稳定机理进行了初步研究，仍然存在一些问题亟待解决，例如双机系统中当送端和受端机组惯量相当时，风电接入如何影响系统暂态稳定性。以后的研究可以对上述问题进行深入分析。

［1］马瑞，周志飞，徐慧明，等.考虑风速特性的动态电压崩溃指标［J］.电力科学与技术学报，2009，24（2）：41-46.MA Rui，ZHOU Zhi-fei，XU Hui-ming，et al.Dynamic voltage collapse index with wind speed considering［J］.Journal of Electric Power Science and Tech-nology，2009，24（2）：41-46.

［2］薛尚青，蔡金锭.风电场不同控制策略对电网电压稳定影响的分析［J］.电力科学与技术学报，2011，26（3）：57-62.XUE Shang-qing，Cai Jin-dian.Impacts of wind farms with different control strategies on power grids voltage stability［J］.Journal of Electric Power Science and Tech-nology，2011，26（3）：57-62.

［3］王世谦，林俐，黄景慧，等.双馈风电机组无功控制方式对系统频率稳定的影响［J］.低压电器，2013（20）：43-45.WANG Shiqian，LIN Li，HUANG Jing-hui，et al.Influence on power system frequency stability from reactive power control mode of doubly-fed wind turbine generator［J］.Low Voltage Apparatus，2013（20）：43-45.

［4］宋战锋，夏长亮.基于定子磁链的双馈风力发电系统矩阵变换器调制策略［J］.电力科学与技术学报，2009，24（3）：10-14.SONG Zhan-feng，XIA Chang-liang.A novel modulation scheme for matrix converters of doubly-fed induction generators based on stator flux［J］.Journal of Electric Power Science and Technology，2009，24（3）：10-14.

［5］田易之，晁勤，高昆.双馈风电机组并网运行的电能质量分析及改进［J］.可再生能源，2010，28（1）：24-28.TIAN Yi-zhi，CHAO Qin，GAO Kun.Analysis on power quality of grid connected doubly fed induction generator and improvement［J］.Renewable Energy Resources，2010，28（1）：24-28.

［6］毕天姝，孔永乐，肖仕武，等.大规模风电外送中的次同步振荡问题［J］.电力科学与技术学报，2012，27（1）：10-15.BI Tian-shu，KONG Yong-le，XIAO Shi-wu.et al.Review of sub-synchronous oscillation with large-scale wind power transmission［J］.Journal of Electric Power Science and Technology，2012，27（1）：10-15.

［7］黎芹，张兴，杨淑英，等.双馈风力发电机低电压穿越转子动态过程分析［J］.电力系统及其自动化学报，2010，22（5）：19-24.LI Qin，ZHANG Xing，YANG Shu-ying，et al.Dynamic behavior of DFIG rotor during low voltage ridethrough［J］.Proceedings of the CSU-EPSA，2010，22（5）：19-24.

［8］石一辉，鲁宗相，闵勇，等.双馈感应发电机三相短路电流解析计算模型［J］.电力系统自动化，2011，35（8）：38-43.SHI Yi-hui，LU Zong-xiang，MIN Yong，et al.Practical calculation model of three-phase short circuit current for doubly-fed induction generator［J］.Automation of Electric Power Systems，2011，35（8）：38-43.

［9］Bu S Q，Du W J，Wang H F，et al.Power angle control of grid-connected doubly fed induction generator wind turbines for fault ride-through［J］.Renewable Power Generation，IET，2013，7（1）：18-27.

［10］卜思齐，杜文娟，王海风.双馈风力发电机故障穿越改进控制策略［J］.电力科学与技术学报，2012，27（1）：33-39.BU Si-qi，DU Wen-juan，WANG Hai-feng.An improved control strategy with ride-through capability for doubly fed induction generators［J］.Journal of Electric Power Science and Technology，2012，27（1）：33-39.

［11］郝正航，余贻鑫.双馈风力发电机组对电力系统稳定性影响［J］.电力系统保护与控制，2011，39（3）：7-11.HAO Zheng-hang，YU Yi-xin.The influence of doubly-fed induction generator on stability of power system［J］.Power System Protection and Control，2011，39（3）：7-11.

［12］Vittal E，O′Malley M，Keane A.Rotor angle stability with high penetrations of wind generation［J］.IEEE Transactions on Power Systems，2012，27（1）：353-362.

［13］Muljadi E，Butterfield C P，Parsons B，et al.Effect of variable speed wind turbine generator on stability of a weak grid［J］.IEEE Transactions on Energy Conversion，2007，22（1）：29-36.

［14］林俐，杨以涵.基于扩展等面积定则的含大规模风电场电力系统暂态稳定性分析［J］.电力系统保护与控制，2012，40（12）：105-110.LIN Li，YANG Yi-han.Analysis of transient stability of power system including large scale wind power based on the extended equal area rule［J］.Power System Protection and Control，2012，40（12）：105-110.

［15］Nunes M V A，Peas Lopes J A，Zurn H H，et al.Influence of the variable-speed wind generators in transient stability margin of the conventional generators integrated in electrical grids［J］.IEEE Transactions on Energy Conversion，2004，19（4）：692-701.

［16］石立宝，戴世强，徐政.大规模双馈型风电场并网的系统暂态稳定仿真［J］.电力系统及其自动化学报，2009，21（4）：1-7.SHI Li-bao，DAI Shi-qiang，XU Zheng.Transient stability simulation with large scale grid-connected wind farms of DFIG type［J］.Proceedings of the CSUEPSA，2009，21（4）：1-7.

［17］Ekanayake J B，Holdsworth L，Wu X G，et al.Dynamic modeling of doubly fed induction generator wind turbines［J］.IEEE Transactions on Power Systems，2003，18（2）：803-809.

［18］贺益康，胡家兵，徐烈.并网双馈异步风力发电机运行控制［M］.北京：中国电力出版社，2012.

［19］Shi Libao，Xu Zheng，Wang Chen，et al.Impact of intermittent wind generation on power system small signal stability［M］.Croatia：InTech，2011.

［20］盛超，曾杰，郝正航，等.含双馈风电场电力系统暂态稳定性分析［J］.电力系统及其自动化学报，2012，24（1）：133-137.SHENG Chao，ZENG Jie，HAO Zheng-hang，et al.Analysis of transient stability of power systems with DFIG-based wind farms［J］.Proceedings of the CSUEPSA，2012，24（1）：133-137.

［21］Kundur P，Paserba J，Ajjarapu V，et al.Definition and classification of power system stability IEEE／CIGRE joint task force on stability terms and definitions［J］.IEEE Transactions on Power Systems，2004，19（3）：1 387-1 401.