坡脚型场地对滑体运动的减速机制研究
2014-01-26曾耀勋樊晓一段晓冬
曾耀勋,樊晓一,2,段晓冬
近年来,随着滑坡频发及惨痛的灾害教训,尤其是滑坡在运动过程中所呈现出的较大差异,吸引国内外学者开始对滑坡运动机理进行思考。目前已提出众多的涉及到滑坡运动固、液、气等诸因素的耦合机制理论模型及基于统计分析方法的经验预测公式[1-7],但大多数耦合机制理论只是针对于某类典型滑坡现象的解释分析,而经验预测公式则仅考虑了不同规模的滑坡运动特征研究,忽略或简化了场地条件对滑坡运动特征的影响,对滑坡灾害的预测预报往往缺乏高精确性及普遍适用性。在野外滑坡现场调查过程中,发现同等规模的滑坡运程存在着较大的差异[8],滑坡启动后的运动特征不仅与总能量(滑坡体积与高差)相关,还显著受运动场地条件控制[9]。
坡脚型滑坡是自然界中发生于坡脚场地条件上的一类常见滑坡,此类滑坡的特征是滑体沿滑动面急速下滑遭遇坡脚,继而改变滑动方向[10-11]。根据文献[12]可以认为当滑体未遭受坡脚约束时的运动特征受总能量显著控制,而造成同等规模滑坡运程差异存在的关键在于滑体遭受坡脚后运动距离的大小,可见坡脚不仅表现为对滑坡运动的阻止效应,而且还关系到滑坡致灾强度评估。因此本研究将利用二维通用离散元程序(universal distinct element code,UDEC)构建基本几何模型,对滑体的运动以及停积过程进行模拟分析,研究坡脚场地条件对滑体运动的减速阻挡机制,以期为滑坡防治提供科学指导及理论依据。
1 离散元理论[13-16]
离散单元法(distinct element method,DEM)属于块体理论数值方法,由Cundall于1971年提出,它的优点是适用于模拟节理系统(岩体)在准静态或动态条件下的变形破坏过程,计算思路不是建立在最小势能变分原理上,而是建立在力的平衡和牛顿第二运动定律基础上,单元之间的相互作用力可以根据力和位移关系求出,而单个单元的运动则完全根据单元所受的不平衡力和不平衡力矩的大小按牛顿运动定律确定。该类方法的基本特征在于允许有限位移和离散块体发生平动、转动、甚至相互分离,弥补了有限元法或边界元法对介质连续和小变形的限制。
UDEC程序是处理不连续介质的二维离散元程序,该程序将岩体的两个基本组成对象(岩块和结构面)分别以连续力学定律和接触定律加以描述,其中接触(结构面)是连续体(岩块)的边界,单个的连续体在进行力学求解过程中可以被处理成独立对象并通过接触与其它连续体发生相互作用,因此能够较好地模拟静载或动载条件下非连续体的运动,而且在模拟计算过程中能够自动识别新的接触关系,适合用来模拟边坡节理化岩体渐进破坏以及失稳后的运动过程。
2 离散元模型
2.1 基本几何模型
在野外滑坡现场调查的基础上,采用离散元程序UDEC模拟坡脚型滑坡运动行为,建立基本几何模型,通过改变坡角α(α=25°,35°,45°,55°,65°)模拟不同的坡脚约束,并设置下部运动场地坡度为5°,概化坡脚场地约束对滑坡运动的影响。在模拟计算过程中,于滑体内选取前、中、后部共计3个监测点,对模拟过程中滑体运动速度及位移进行监测。
2.2 模型处理
本次离散元模拟主要考察坡脚型场地对滑体运动的减速机制,再现滑体遭受坡脚约束乃至停积的过程,在模拟计算过程中块体划分及边界条件处理的原则和过程为:滑体失稳启动后,由于滑体单元自身变形相对于运动位移很小可以忽略不计,因此可以采用刚性本构模型,即滑体是由一些被节理切割的块体单元组成,块体间在此仅考虑摩擦系数及黏聚力,而对于下垫面参数则仅考虑摩擦系数,并在计算过程中块体均保持形状和大小不变。在接触关系上,则选用库伦滑动模型及其本构关系,该本构模型适合于模拟松散和粘结颗粒材料,如土、岩石以及混凝土。同时为使滑体在所设计的几种坡角条件下都能够失稳启动,利用工程类比法并在计算过程中经过不断调整得出具体的模型材料及节理物理力学参数详见表1—2。边界条件设置如下,在模型中对整个滑床采用全约束,即无水平位移以及垂直位移,而对滑体单元则不加约束,允许其转动,甚至脱离接触而解体,重点研究滑体遭遇坡脚后的减速运动阶段。并利用对滑体右部添加固定位移边界的模拟挡板,初始平衡后,利用Free命令释放该边界条件,即可模拟滑体失稳启动。上述假设对滑体失稳后运动实际情况,即应力发生全面松弛的现象是较为合理的。

表1 滑体物理力学参数

表2 下垫面物理力学参数
3 坡脚对滑体运动特征的影响
3.1 坡脚对运距L′的影响
对于坡脚型滑坡,同等规模滑坡运程出现差异的关键在于滑体遭受坡脚阻挡后运动距离的大小。因此在此统计了不同坡角条件下滑体遭受坡脚阻挡后的运距L′,即堆积体前端离坡脚的最大水平距离。可以发现,不同坡角条件的运距L′存在着较大的差异,从大到小顺序依次为:L′(45°)> L′(35°)> L′(25°)>L′(55°)>L′(65°)。表明滑体减速阶段的运距L′,随着坡角的增加而增加,并当增加到一定角度后,增加坡角则将造成运距L′急剧减小。
3.2 监测点减速特征对比
为更加深入地探讨坡角条件对滑体的减速机制,分别统计了不同坡角条件下各监测点的减速曲线分布(如图1—5所示)。
图1表明滑体在25°坡角条件下,前部,中部和后部这3点的减速曲线均较为缓和。这是由于滑体在该坡角下,速度增量集中于水平方向,由此遭受坡脚所受的约束阻挡程度较小,滑体未出现强烈撞击导致解体的现象,但由于在整个减速阶段整体持续受到坡脚的摩擦约束,不同于较大坡角中出现的能量传递及集中于滑体某部致使其脱离接触的现象,因此摩擦损耗能较大,导致运距L′偏短。
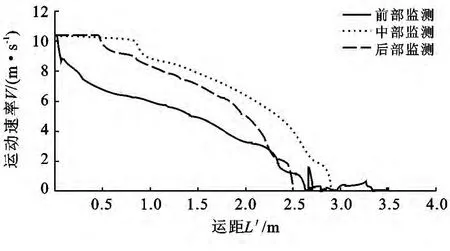
图1 滑体监测点减速特征对比(α=25°)
从图2可以看出,在35°坡角条件下滑体的前部与滑体中后部的减速曲线存在较大的差异。这是由于滑体遭受到坡脚时的破坏机制为滑体前部滑速急剧下降,在该瞬间滑体前部与中后部产生了较大的速度差,速度差的存在使得中后部对前部产生巨大的挤压和撞击力,使前部高速运动甚至飞行,即中后部能量传递并集中于前部。图2中滑体前部测点在初始位置速度近乎垂直下降后出现上下波动,并在随后维持了较长持速阶段,符合高速凌空飞越空气动力擎托持速机理[17],以及从中、后部测点较为迅速降至为零也可以得到体现,由此造成该坡角条件下的运距L′增大。
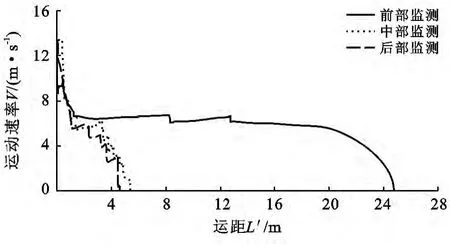
图2 滑体监测点减速特征对比(α=35°)
图3 则表明在45°坡角条件下所呈现出的减速特征有点类似于35°坡角条件,但又有不同之处,滑体前部并未出现较长的持速阶段,而滑体中部却呈现出持速的特征。这是由于该坡角条件下,滑体急速下滑遭受坡脚时的破坏机制发生改变造成的,巨大撞击反作用力作用于滑体,致使滑体中部受滑体后部挤压撞击以及前部阻挡二者耦合作用下,并在此过程中滑体后部能量传递给中部,滑体中部被折断弹出呈飞行态,飞行运动较长距离后落地停积,由此造成运距L′增加。而造成35°坡角与45°坡角运距存在差异的原因则在于两者起飞机制不同,前者属于撞击高速擎托式(能量损耗相对较大),而后者则属于剪断弹飞式(能量损耗相对较小),因而后者的初始飞行速度相对前者更大。

图3 滑体监测点减速特征对比(α=45°)
图4 —5分别为55°与65°坡角条件下各监测点沿减速阶段运距L′的速度特征对比,可以发现此两者呈现出较为类似的特征,减速曲线均存在着较大的波动,这是由于当坡角超过45°后,在垂直方向上的速度增量开始占优,并随着坡角的增大,总能量转化为垂直方向上的动能比例随之增大。当遭受坡脚约束时,滑动方向转化为接近水平,垂直方向速度减小近乎零,因而坡角越大,其受坡角阻挡约束所损耗的能量也越大,滑体迅速停积,造成运距L′减小。
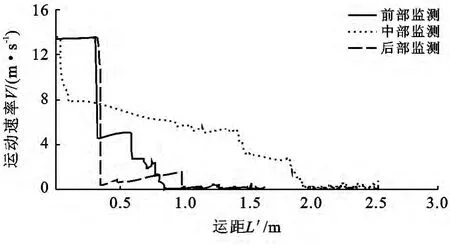
图4 滑体监测点减速特征对比(α=55°)

图5 滑体监测点减速特征对比(α=65°)
通过对上述各监测点减速特征的对比分析可知,坡脚导致同等规模滑坡运程差异的关键在于减速阶段运距L′的差异,而滑体在坡脚处的破坏机制引发的能量传递及集中现象则决定着滑坡减速阶段运距L′的长短。
4 摩擦系数对滑体运动特征的影响
在此选择45°坡角的基本几何模型,研究坡脚型场地的摩擦系数,即下垫面摩擦系数对滑体运动的减速机制,主要对不同下垫面摩擦系数下的堆积体分布形态进行监测(图6)。由图6可以看出,下垫面摩擦系数越高,堆积体的整体性越高,如f=0.75时,滑体保持相对完整。而f=0.05时,滑体前中部则完全解体呈碎屑状平铺于坡面,而后部保持相对完整。表明下垫面摩擦系数越低,位能转化为动能的程度越高(最高速度越大),遭遇坡脚后滑体解体碎屑化更加严重,碰撞更为频繁,引起能量传递及集中的程度也更高,造成运距也随之剧增。
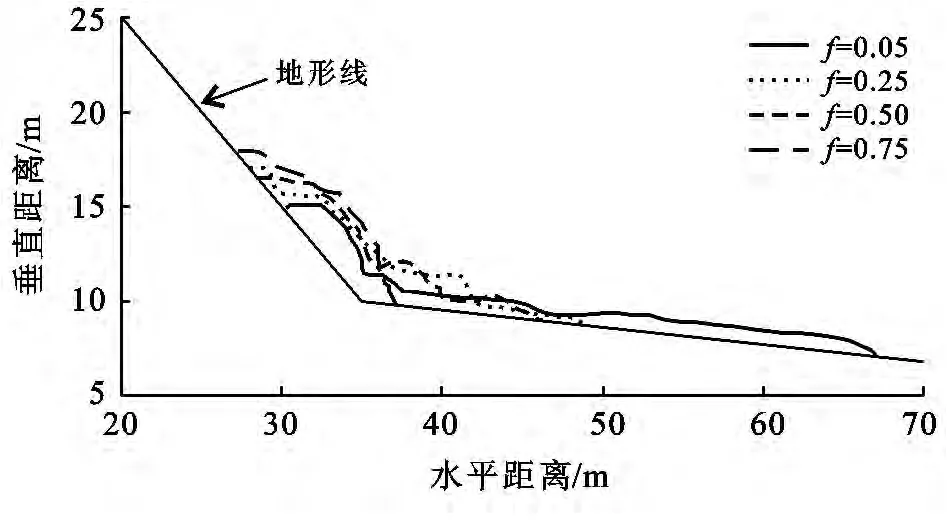
图6 下垫面摩擦系数f与堆积体的关系
5 结论
(1)坡脚型滑坡在同等规模下运距存在差异的关键在于不同坡角条件下滑体遭遇坡脚后减速阶段的运距L′的大小。在下垫面摩擦系数一定的条件下,运距L′与坡角α密切相关,随着初始坡角的增加而增大,但当增加到一定角度后,随着坡角的增加将会造成运距L′急剧减小。
(2)不同坡角条件下滑体的减速曲线分布存在较大的差异,这与滑体受坡脚约束阻挡以及在此处的破坏机制不同有关,同时也反映出能量传递及集中现象是决定运距L′长短的关键。
(3)下垫面摩擦系数也是影响滑体运动特征的重要因素,控制着滑体的最终堆积体形态,其一般规律为下垫面摩擦系数越低,位能转化为动能的程度越高,遭遇坡脚后滑体解体碎屑化更加严重,由此造成滑体总运距随之增加。
[1] Legros F.The mobility of long-runout landslides[J].Engineering Geology,2002,63(3):301-331.
[2] Deline P.Interactions between rock avalanches and glaciers in the Mont Blanc massif during the late Holocene[J].Quaternary Science Reviews,2009,28(11):1070-1083.
[3] Hungr O.Rock Avalanche Occurrence,Process and Modeling[M]∥Landslides from Massive Rock Slope Failure.Netherlands:Springer,2006.
[4] 王念秦,张悼元.一种典型黄土滑坡的滑距预测方法[J].西北大学学报,2003,33(1):111-114.
[5] 方玉树.高位能滑坡运程探讨[J].后勤工程学院学报,2007,23(4):16-20.
[6] 廖小平.高速滑坡滑体体积与滑速滑程的相关研究[J].路基工程,1994(6):9-12.
[7] 乔建平,赵宇,陈永波.典型滑坡的研究方法[J].山地学报,2003,21(3):369-372.
[8] 苟富刚,王运生,吴俊峰,等.都江堰庙坝地震高位滑坡特征与成因机理研究[J].工程地质学报,2012,20(1):21-28.
[9] 樊晓一,乔建平.“坡”、“场”因素对大型滑坡的运动特征影响研究[J].岩石力学与工程学报,2010,29(11):2337-2347.
[10] 许强,裴向军,黄润秋,等.汶川地震大型滑坡研究[M].北京:科技出版社,2009.
[11] 黄润秋,许强.中国典型灾难性滑坡[M].北京:北京科技出版社,2008.
[12] 樊晓一.地震与非地震诱发滑坡的运动特征对比研究[J].岩土力学,2010,31(S2):31-37.
[13] 蔡跃,三谷泰浩,江琦哲郎.反倾层状岩体边坡稳定性的数值分析[J].岩石力学与工程学报,2008,27(12):2517-2522.
[14] 曹琰波,戴福初,许冲,等.唐家山滑坡变形运动机制的离散元模拟[J].岩石力学与工程学报,2011,30(S1):2878-2887.
[15] 雷远见,王水林.基于离散元的强度折减法分析岩质边坡稳定性[J].岩土力学,2006,27(10):1693-1698.
[16] 肖克强,李海波,刘亚群,等.地震荷载作用下顺层岩体边坡变形特征分析[J].岩土力学,2007,28(8):1557-1564.
[17] 程谦恭,胡厚田.剧冲式高速滑坡全程动力学机理分析[J].水文地质工程地质,1999(4):19-23.
