在高等数学课堂中培养创新思维的探讨
2014-01-24郭楠
郭 楠
(南京工程学院 数理部,江苏 南京 211167)
在高等数学课堂中培养创新思维的探讨
郭 楠
(南京工程学院 数理部,江苏 南京 211167)
介绍了高等数学课堂中培养创新思维的重要性,并结合本人的教学实践,提出一些有效的方法。
高等数学;教学方法;创新思维
1999年6月13日,中共中央国务院关于深化教育改革全面推进素质教育的决定中明确指出:“高等教育要重视培养大学生的创新能力、实践能力和创业精神”[3]。因此,提高学生综合素质、培养学生创新思维能力的改革就凸显得极为重要。
《高等数学》是大学本科理工科非数学专业必修的一门经典数学课程,是一门学时多、涉面广的重要的基础课。它的理论和方法是研究客观世界中连续模型的数学基础。在各领域中的应用也越来越广泛,对高校人才培养的质量起着举足轻重的作用。那么如何在高等数学教学中培养学生的创新思维是一个具有重要理论意义和实际应用价值的研究课题。下面我就谈谈在高等数学课堂上如何培养学生创新思维的一些想法和尝试。
一、激发学生的学习兴趣
学习兴趣是自觉的、内在的激励学习的动力。只有当学生喜欢学,他们才会主动吸取知识,愿意坚持下去。如果没有学习兴趣,就不可能好的学习成果。如何让学生喜欢数学,教师首先要研究并提高自己的教学艺术,采取合适的教学方法,引导学生欣赏数学之美、品味数学之趣、感受数学之妙、领略数学之奇,展现数学的魅力,激发学生对数学的学习兴趣,让学生在学习数学的过程中体验数学思考的乐趣和数学文化的魅力。
在教学中,可结合教学内容,适当介绍数学史、数学思想,使学生了解前辈数学家的思考轨迹,激发学生的学习积极性。比如我们在讲到洛必达法则时,引申到他对微积分的贡献,并介绍了洛必达的生平,不仅使学生了解到洛必达的数学才华,而且对于鼓励学生努力学习,不断创新也起到了积极作用。再如定积分概念中“分割,取值,求和,取极限”的过程,就包含着“化整为零,局部以不变代变,化零为整,极限”的思想。
教学中,不仅讲解定理、结论,还要介绍结论的发现过程,讲解知识背景。由于高等数学教材习题中主要是计算题,应用题很少,所以可以适当的调整,适当减少练习技巧的计算题,增补联系实际,特别是联系专业实际和当前经济发展的实际的应用题。
二、培养学生主动思考的习惯
心理学认为,人的知识是通过人本身内部的建构获得的。传播与交流的知识,只有在被接受者内化,即与学习者头脑中已有的知识联系起来,重新建构之后,而得到理解与掌握,并加以运用。高等数学基本理论的教学包括基本概念、基本定理、公式、法则的教学。概念的形成、定理的证明、公式的推导和法则的导出都必须经过学生本人的积极的思维活动。与已有的知识联系起来,经过抽象、推理,建立起新的关系,重新建构自己头脑中的认知结构。高等数学主要是课堂教学,传统的教学模式是老师讲、学生听,一味的“注入式”、“填鸭式”教学。这种方式培养出来的学生往往懒于思考,实际应用能力、创新能力差。
1.加强启发性。培养学生创新能力的一个重要方面是让学生会思考,会提问题。教师在教学中要着重培养学生的质疑能力和科学批评精神。老师设置问题,引导学生思考、回答。比如:在进行“洛必达法则的证明”教学时,老师问:“函数和导数之间的桥梁是什么?”学生答:“微分中值定理。”老师问:“选择哪个中值定理呢?观察一下洛必达法则的形式。”学生答:“这是函数之比的形式,选用Cauchy中值定理。”再比如讲解用导数判断单调性时,老师可以利用图形,让学生寻找、发现导数与单调性的关系。
设置合适的问题情境,可以让学生自己去发现,同时学生在探索知识的过程中创新思维能力也能得到提高。
2.加强学生的发散思维。发散思维,是对同一问题从不同方向来探求的思维过程,是培养学生创新思维的重要环节。在高等数学的教学中,可以从下面几方面加强学生的发散思维能力:为学生提供合适的开放性问题,让学生自由选择、自主发现;加强一题多解、一题多变、举一反三的联系,等等。比如,在讲授完导数的应用,可以举例:当x≥-1,1>α>0时,证明:(1+x)α≤1+αx。可以由中值定理、单调性、极值最值、凹凸性完成。让学生在学习的过程中,要善于思考、总结、联想。
三、教学手段的多样化
在高等数学的课堂教学中,基本上是老师讲学生听的单一模式,当然也要避免“放映员式”的上课模式。要根据不同的教学内容和教学对象,采取不同的教学方式,将传统的板书和多媒体直观演示有机结合,增强课程教学效果。
从教学实际出发,在合适的教学内容中将多媒体课件引入教学是非常必要的。比如了解函数的图像、性质;导数和微分的几何意义、物理意义;定积分定义中的分割、近似、求和、取极限的过程等等,采用课件的形式进行分析,更加直观、形象,有助于提高学生对高等数学的理解和思考能力,从而提高学生的创新思维能力。

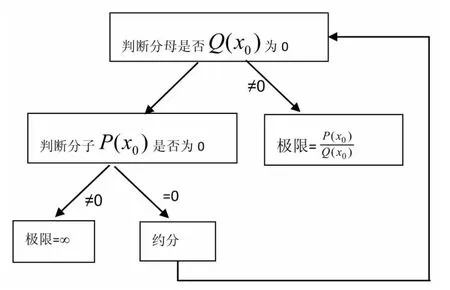
感兴趣的同学还可编个小程序。这种多角度的教学模式既便于学生总结方法,又激发学生学习兴趣。
总之,在高等教育重视应用能力、素质能力培养的当下,我们必须在高等数学教学中不断的摸索、总结教学方法和手段,从而提高学生的创新精神和创新能力。
[1]张奠宙.高等数学教育中的“创新”工程大纲[M].北京:高等教育出版社,1999:4.
[2]朱士信.如何在大学数学课堂教学中培养学生创新思维[J].大学数学,2003,19(3):30-33.
[3]关于在工科数学教学中培养学生创新思维能力的思考与尝试[J].大学数学,2008,24(4):1-4.
G642.0
A
1674-9324(2014)26-0217-02
南京工程学院教改项目——微课在高等数学教学中的应用。
郭楠(1983—),女,江苏靖江人,讲师,硕士,任职于南京工程学院数理部,研究方向:非线性优化。
