启发式教学在《离散数学》中的应用
2014-01-24杨秋芬
杨秋芬,杨 芳
(湖南广播电视大学 理工教学部,湖南 长沙 410015)
启发式教学在《离散数学》中的应用
杨秋芬,杨 芳
(湖南广播电视大学 理工教学部,湖南 长沙 410015)
启发式教学以学生为中心,调动学生学习的主动性、积极性,培养学生的创新思维。本文结合自己的教学实践,论述启发式教学在《离散数学》中的应用,并试图把计算机多媒体技术运用于《离散数学》的教学中,以求得到最佳的教学效果。
启发式教学;问题情境;创新思维
一、引言
《论语·述而》中有“不愤不启,不悱不发”,这是启发式教学“启发”的原始出处。“愤”——学生对某一问题积极思考,急于解决而又尚未解决的矛盾心理状态;“启”——教师对处于“愤”的学生加以点拨,帮助学生开启思路;“悱”——学生有自己的思考,但尚未成熟的心理状态;“发”——教师帮助学生弄清事物的本质属性,使学生柳暗花明,豁然开朗。这里的关键是问题情境,它是指个体面临的刺激模式与其已有知识结构所形成的差异。
启发式教学同“注入式教学法”根本对立,它以学生为中心,让学生主动提出问题、思考问题,自己去发现、探索,教师只是从旁边加以点拨。启与发是因与果的辩证关系,启是因,发是果。教师要启而得法,学生才能启而即发,主动动手、动脑、动口去获取知识。因此,启发式教学是教学过程中教师与学生共同掌握知识、培养学生的创新思维,而如何创设问题情景才能达到教师启而得法的效果,是所有老师的目的所在。
二、《离散数学》的目的和性质
《离散数学》是中央电大计算机应用专业计算机信息管理方向必修的专业基础课程。它是学习后续专业课程必须的数学工具。该课程是一门理论性和应用性兼备的课程,它根据计算机学科的特点,着重研究离散数据结构及相互关系,为计算机专业后续课程的学习做好必要的知识准备,进一步提高学生的抽象思维和逻辑推理能力,为从事计算机的应用提供必要的描述工具和理论基础。
三、启发式思维在《离散数学》中的应用
图论是《离散数学》独立的一部分,是一门具有实用价值的独立学科,它有广泛的研究课题,在语言学上、逻辑学、物理化学、信息学以及通信工程等方面有广泛的应用;并且在计算机开关理论与逻辑设计、数据结构等方面起重要作用。图论中的概念多,有向图、权图、二叉树、最小树、最短路等都可以使用启发式教学,充分调动学生的学习积极性,创设良好的问题情境,对于激发学生的学习热情和学习需要能够产生有效的激励作用。本人连续9次在电大普专科、专升本班讲授《离散数学》,采用启发式教学,因材施教,及格率都在95%以上,深受学生好评。下面以图论中的最短路算法为例,讲述问题情境的创设及启发式思维的教学过程。
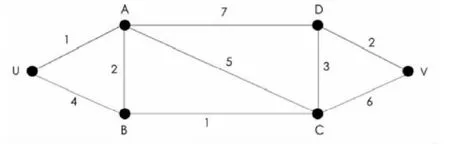
图1 求最短路的示例图
“愤”——问题情境:假设此图是城市之间的旅游费用图,那么从U到V的最少费用是多少?(这里的最少费用对应最短路)
“启”——尽管电大学生基础差,没有学习过《数据结构》,不知道什么是算法;但好玩是年轻人的共同爱好。学生很快算出是9。
“悱”——请学生看中央广播电视大学出版社出版的《离散数学》P228的Dijkstra迪克斯特拉算法,都不清楚是怎么回事。

重复执行此过程,直到求出了所有距离和最短路为止。
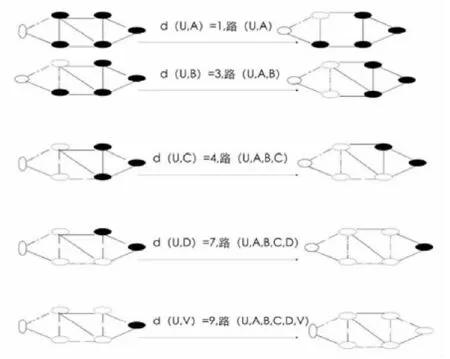
图2 求最短路的流程图
在上题中,用白圈代表已在最短路上的节点,黑圈代表没有进入最短路的节点。
此题中最短路只有一条,但在具体的执行过程中,最短路可能不唯一,正如旅游线路可能不止一条一样。
四、结束语
计算机多媒体技术是把声音、文本、图形、图象、动画、影象等各类信息进行快速加工、整合、演播和传输的综合技术,是Internet上最热门的技术,以其信息载体的多样性、集成性和交互性等特性,在教学中发挥着巨大的作用。
[1]王海瑞,李亚,张智斌,等.基于CDIO的《计算机组成原理》教学改革探讨与实践[J].教育教学论坛,2011,(30):21-22.
[2]王海瑞,李亚,张智斌“.计算机体系结构”课程教学建设与改革方法探讨[J].教育教学论坛,2011,(29):22-24.
[3]周红萍,高晓芳.大学生就业压力与择业研究[J].辽宁行政学院报,2008,(02).
G642.0
A
1674-9324(2014)26-0138-02
book=26,ebook=205
湖南省十二五规划课题(项目编号:XJK013BXX006)。
杨秋芬(1973-),女,湖南广播电视大学副教授,博士。
