关于轴承预紧力对轴系性能影响的仿真分析

李颂华，冯明昊

（沈阳建筑大学 交通与机械工程学院，辽宁 沈阳 110168）

0 引言

主轴系统是机床的核心功能部件之一。对主轴轴承施加预紧力不仅能够消除轴承的轴向间隙，降低振动噪声，提高支承体旋转精度，控制滚动体的自旋滑动，减少滚动体的公转打滑，进而提高轴系刚度，降低轴系振动，而且还能够提高主轴系统的临界转速和机床的加工精度。然而，轴承预紧力施加的太大就会加剧轴承发热，降低轴承的使用寿命并引起主轴温升和热变形的增大，尤其是在主轴高速旋转时这种状况会更加明显；轴承预紧力施加的太小又不能充分发挥主轴系统的潜能[1]。因此，关于轴承预紧力的研究对提高主轴系统的综合性能具有重要意义。

本文对不同预紧力下的轴承刚度进行了理论计算，并对不同预紧力下的主轴轴承系统进行了模态和谐响应分析。

1 轴承刚度的理论计算

根据机床的不同类型，高速主轴轴承具有多种配置方式，实验室对原有磨削电主轴进行了轴承预紧力施加改造，如图1 所示。主轴前后端各配置一个轴承，采用背对背配置方式。使用压电陶瓷微位移驱动器对轴承施加预紧力，采用应变片压力传感器检测所施加轴承预紧力的大小，使用热电偶检测轴承的温升。

图1 电主轴轴承预紧力施加结构图

角接触球轴承在轴承预紧力Fp的作用下，接触角由α0变成α1，计算公式[2]为：

式中： c—接触变形因数；fm—内外滚道曲率比的平均值，fm=（ri+re）/（2Dw）；α0—初始接触角；α1—变形后的接触角；DW—轴承滚珠直径；Z—轴承滚珠数量。将式（1）转变为：

本文的电主轴采用7009C 轴承，初始接触角为15°。式（2）等号右侧能够根据相关参数直接计算得出，等号左侧的α1通过迭代计算，进而求出轴承施加预紧力之后的接触角。轴承轴向和径向刚度通过公式 （3）～（5）[2]计算：

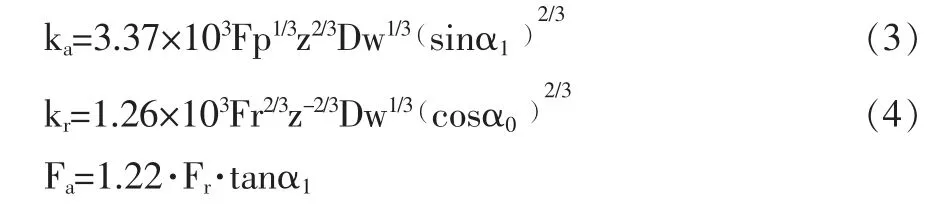
式中： Fa和Fr—轴承的轴向和径向载荷。为了方便计算，本文使用VB6.0 编写了相应的计算程序软件，以便快速计算出了在不同预紧力下轴承的轴向刚度和径向刚度，如表1 所示。从表中可以看出，轴承的轴向和径向刚度都随轴承预紧力的增加而增加。

表1 预紧力与轴承刚度

2 模型的建立

求出预紧力与轴承刚度的关系后，本文利用有限元法对轴系进行模态和谐响应分析。由于是对同一轴系进行分析，所以谐响应分析与模态分析模型完全相同。

在轴系有限元模型中将轴承模拟为弹簧单元，通过设置不同预紧力下的轴承刚度值，运用静力学分析求解轴系的固有频率。有限元建模过程[3]如下：

（1）主轴预处理。将孔、槽和螺纹等按实体处理，将各处倒角简化为直角，忽略空刀槽，在不影响计算结果的前提下保证网格模型的规则划分和可求解性。

（2）附加质量的处理。将电机的转子及平衡环等效为同密度轴材料，作为主轴的附加分布质量，等效到所在单元的节点上[4]。

（3）轴承等效处理。每个轴承可等效为4 个轴向分布和4 个径向分布的弹簧单元，如图2 所示。弹簧的长度为轴承内、外半径之差，位置点在轴承法线与主轴中心线的交点。弹簧单元参数有刚度（轴承的轴向刚度Ka与径向刚度Kr）和阻尼。

（4）轴系有限元模型建立和网格划分。选取合适网格的划分尺寸，在主轴某一半剖面内用平面单元（如PLANE42）进行网格划分；再通过旋转用三维实体结构单元 （如SOLID45） 进行网格划分。

（5）如图3 所示，将弹簧单元的外接点全部固接。

图2 轴承的等效处理

图3 轴系有限元模型

3 轴系固有频率的仿真计算

3.1 固有频率仿真计算的理论基础

模态分析用来确定结构或构件的振动特性，即固有频率和振型[5]。为了能更好地进行理论分析，必须建立能够真正反映振动系统实际情况的动力学模型和对应的数学模型，再根据数学模型求解系统的特征向量初特征值（固有频率）。多自由度的运动微分方程：

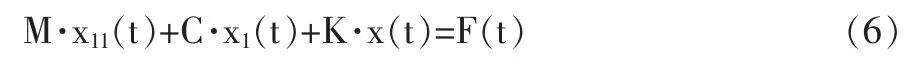
式中： M、C、K—系统的质量、阻尼、刚度矩阵；x11（t）—系统的振动加速度矩阵；x1（t）—系统的振动速度矩阵；x（t）—系统的振动位移矩阵；F（t）—系统的载荷向量矩阵。

当F=0 时，求解齐次方程得到的通解将反映系统的自由振动特性，求解它所对应的特征方程得到系统特征解将反映结构的固有特性。

当F≠0 时，求解非齐次方程得到方程的特解将反映输入载荷的特点。

固有频率只与系统本身特性有关，当外载荷F（t）=0时，系统的微分方程：

求解微分方程的广义特征值便是系统的固有频率。

3.2 固有频率分析计算

在ANSYS 中有多种模态提取方式，本文采用Block Lanczos 法。Block Lanczos 法功能强大，尤其对于提取大型模型中的大量振型非常有效。它经常应用在具有实体单元或壳单元的模型中，在具有或没有初始截断点时同样有效（允许提取高于某个给定频率的振型），还可以很好的处理刚体振型。

轴承在不同预紧力下拥有不同的轴向和径向刚度，进而对轴系的固有频率有不同的影响。本文首先计算出轴承在不同预紧力下的轴向和径向刚度，在对模型中模拟轴承的弹簧施加不同的刚度，最终获得不同预紧力下轴系的固有频率。轴系在不同预紧力下有多阶固有频率，本文只考虑一阶频率。计算结果如图4 所示。从图中可以看出，轴系的一阶频率随着轴承预紧力的增大而增大。同时随着轴承预紧力的增大，轴系一阶频率的增长速度变慢。说明对轴承施加预紧力能够提高轴系的固有频率。这为为提高轴系临界转速而选择轴承预紧力大小提供理论参考。

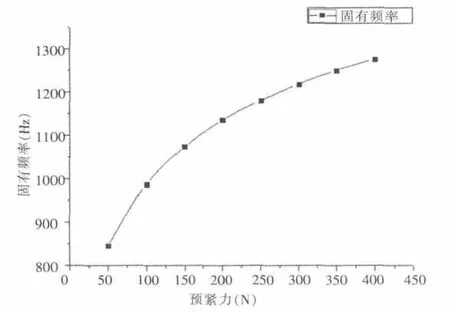
图4 轴承预紧力与轴系固有频率

4 轴承预紧力对轴系振动的影响

4.1 谐响应分析理论基础

谐响应分析是用于求解一个线性结构在已知频率的正弦载荷作用下结构稳态相应的技术。该技术只计算结构的稳态受迫振动，不考虑结构在激励开始时的瞬态振动。谐响应分析预测结构的持续动力特性，从而能够验证此结构是否能够克服疲劳共振及其他受迫振动引起的有害影响。

谐响应分析为输入谐波载荷（力、压力和强迫位移），输出每一个自由度上的谐响应（如位移、应力和应变等），其动力学运动方程：

式中：[M]—质量矩阵；[C]—阻尼矩阵；[K]—刚度矩阵；{u11}—节点加速度向量；{u1}—节点速度向量；{u}—节点位移向量；{F（t）}—载荷为时间的任意函数。对简谐运动而言，{u}和{F}均为简谐形式，设其频率为ω，则有：

将式（9）和（10）代入式（8），可得谐响应分析的运动方程：

由此可见，当所施加载荷的虚部非零时，谐响应分析得到的响应解均是复数形式。

4.2 谐响应分析计算

在ANSYS 中有三种谐响应分析方法： 完全法、缩减法和模态叠加法。其中模态叠加法通过对模态分析得到振型（特征值），再乘上系数并求和，来计算结构的响应，并且计算速度快。本文的采用模态叠加法进行谐响应分析计算。

在激振力的作用下，轴系在其固有频率处会发生共振并产生响应位移。本文对不同预紧力下轴系一阶频率的响应位移进行了计算分析，选取的激振力Fr=100N，在主轴前段加载。

图5 主轴前段径向响应位移

图5 是轴系在不同预紧力作用下，主轴前段、主轴后端和主轴中间的径向响应位移。从中可以看出，主轴前段和后端的径向响应位移随着轴承预紧力的增大而降低且降低速度逐步减小；主轴中间的径向响应位移随着轴承预紧力的增大而增大且增长速度减慢。说明对轴承施加预紧力能够降低主轴前段和后端的振动，同时也会提高主轴中间的振动。这为轴系的优化设计提供理论参考。

5 结论

基于实验室的磨削电主轴完成了不同轴承预紧力下轴承刚度的计算，并对磨削电主轴轴系在不同轴承预紧力下进行了模态和谐响应仿真分析计算。结果表明： ①轴承的刚度随着轴承预紧力的增加而增大；②轴系的固有频率随着轴承预紧力的增加而增大；③主轴前段和后端的响应位移随着轴承预紧力的增大而减少，而主轴中间的径向响应位移随着轴承预紧力的增大而增大。

[1]蒋书运.预紧力可控智能化高速加工电主轴[P].中国ZL200610-038219.6. 2006,10,18.

[2] [日]冈本纯三，黄志强. 球轴承的设计计算[M]. 北京：机械工业出版社，2003.

[3] 刘显军，洪军，朱永生，刘志刚. 多支承轴系轴承受力与刚度的有限元迭代计算方法[J]. 西安交通大学学报，2010，11.

[4] 胡爱玲. 高速电主轴动静态特性的有限元分析[D].广东：广东工业大学机械工程学院，2004.

[5]刘伟，高维成，于广滨.ANSYS12.0 宝典[M]. 北京：电子工业出版社，2010.

[6] 张珂，佟俊，吴玉厚，等. 陶瓷轴承电主轴的模态分析及其动态性能实验[J]. 沈阳建筑大学学报（自然科学版），2008，3.

[7] Young-Kug Hwang and Choon-Man Lee. A Review on the Preload Technology of the Rolling Bearing for the Spindle of Machine Tools[J]. International Journal of Precision Engineering and Manufacturing，2010，3.

[8] Shuyun Jiang, Shufei Zheng. A modeling approach for analysis and improvement of spindle-drawbar-bearing assembly dynamics[J].International Journal of Machine Tools & Manufacture. 2010，50.