基于二元线性回归的人体尺寸查询系统设计研究

张春红，郭 磊，刘艳霞

（电子科技大学 中山学院，广东 中山 528402）

0 引言

人性化是产品设计的必然趋势和发展方向[1]。为实现以人为本的产品设计，首先要进行人体尺寸参数研究。人体尺寸参数之间，如人的年龄与身高之间，身高和体重之间，都存在一定的相关关系。对相关关系规律的研究，主要有相关分析和回归分析两种方法[2]。相关分析主要表达两者相互依存关系的方向和密切程度；回归分析是根据相关关系的具体形态，建立一个合适的回归方程，用来近似地表示变量间的平均变化关系的一种统计分析方法。为方便设计尺寸获取，根据产品设计要素，对我国成人主要人体参数进行相关分析和回归分析研究，并开发基于身高和体重的二元线性回归的人体尺寸查询系统,实现根据人的身高和体重两个基本尺寸参数，查询人体各环节主要尺寸参数，为产品的人性化设计提供便利。

1 研究思路

基于二元线性回归的人体尺寸查询系统设计研究思路如图1 所示。

图1 研究思路

首先分析产品设计中较常用到的人体尺寸以及中国成人的尺寸数据源；其次分析人体各环节的尺寸参数与身高和体重的关系，通过相关分析和回归分析，并建立相应的回归方程；最后进行查询系统开发。

2 人体尺寸数据来源及整理

人体尺寸数据主要有以下几个来源： GB10000-88提供的中国成人人体基础数据和中国人解剖学数值[3，4]。为了计算和表达的方便，把人体按骨性标志划分为15个环节： 头颈部，上躯干，下躯干，左上臂，左前臂，左手，右上臂，右前臂，右手，左大腿，左小腿，左足，右大腿，右小腿，右足[5]。每个环节对应的人体尺寸均可从数据源查询或整理计算得出。

3 人体尺寸参数间的分析

对人体尺寸参数间的分析主要是人体各环节尺寸与身高体重两基本尺寸间的相关分析和回归分析。

3.1 相关分析

人体各环节尺寸与身高和体重均存在着明显的相关关系。为进一步研究两个尺寸变量之间相互关系的密切程度，对人体各环节尺寸与身高和体重间进行线性相关分析，通过计算其线性相关系数即皮尔逊(Pearson) 相关系数r 表示[6]。相关系数的绝对值|r|在0.3 以下是无直线相关；0.3～0.5 是低度直线相关；0.5～0.8 是显著相关；0.8 以上是高度相关。皮尔逊相关系数的计算公式为：

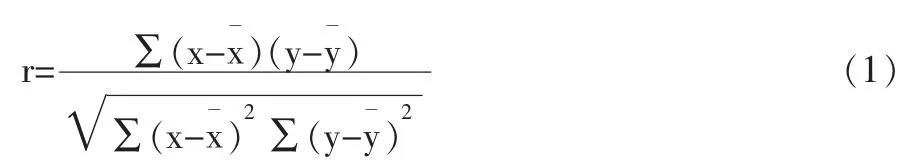
在实际计算中，常用另一公式来直接计算：

3.2 回归分析

通过回归分析，建立相应的回归方程，可表达出因变量受到自变量的影响程度。在研究人体尺寸参数间的关系时，采用的是基于身高和体重的二元线性回归分析，建立的是二元线性回归方程。其数学表达式为：

其中，B0，B1，B2是与X1，X2无关的常数；B0是回归方程常数项；B1，B2是回归系数。X1，X2是2 个自变量，Y 是因变量。为了求得参数B0，B1，B2常常采用的是最小二乘法原理的估计方法，详细方法可参见一般的数理统计教材，也可借助软件完成。在研究人体尺寸参数间关系时，把身高（mm）X1和体重（kg）X2作为自变量，各环节尺寸作为因变量Y。通过Excel 软件计算分析，得到我国成年女性关于身高和体重两基本尺寸的二元线性回归方程为： 上臂长（Y）=-97.694+0.234 身高（X1）+0.239体重（X2）。

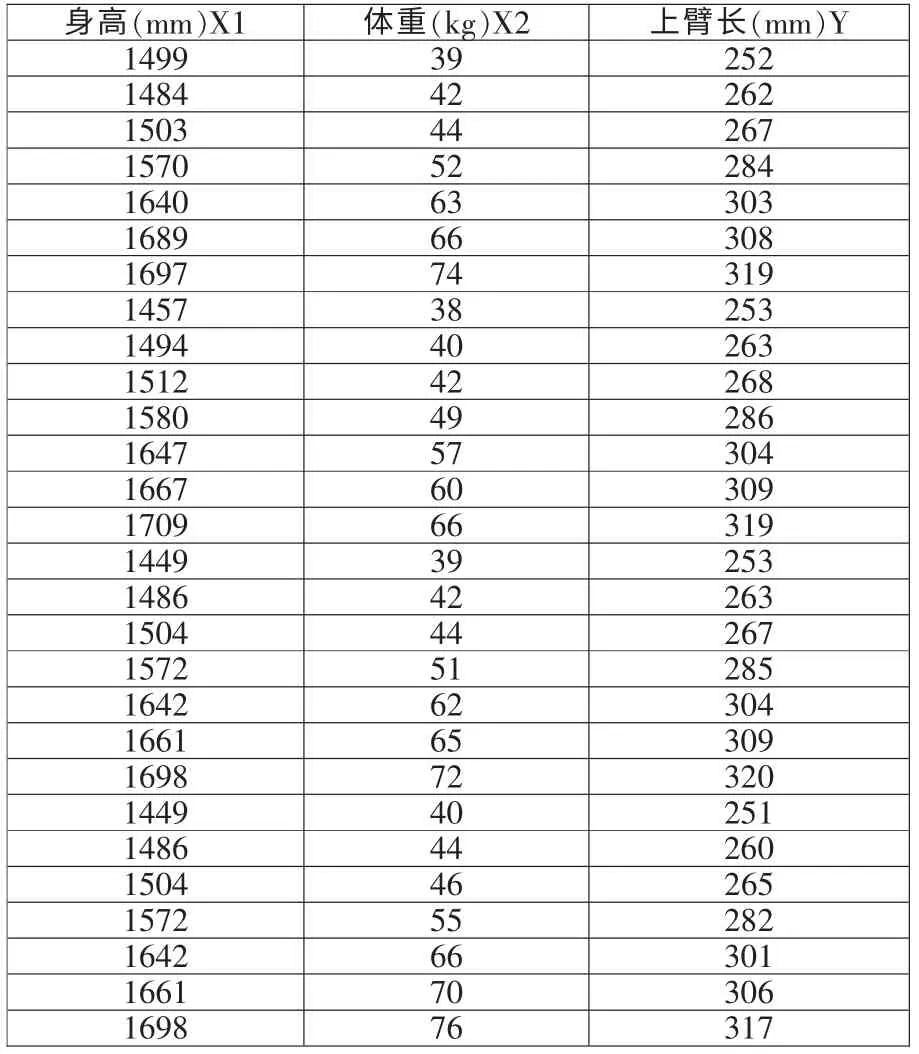
表1 我国成年女性的上臂长与身高、体重间的相关系数

?

依照类似的方法，对我国成年男性和女性的各环节其他主要尺寸参数与身高和体重两基本尺寸之间进行类似的相关分析和回归分析，建立二元线性回归方程，为人体主要尺寸参数查询系统开发做好前期准备。

4 人体主要尺寸参数查询系统开发

开发的查询系统可根据身高（单位：mm）和体重（单位：kg）两个基本尺寸参数查询人体各环节主要尺寸参数。系统采用Visual C++ 开发工具进行开发，适合在Windows 环境下运行。

4.1 查询项目

结合产品设计要素，各环节主要尺寸参数的查询项目有： 长度、围径、体积、质量和质心以及转动惯量。其中长度包括15 个环节中每个环节的长度，但由于人体具有左右对称结构，因此共9 项，分别为： 头颈、上躯干、下躯干、上臂、前臂、手、大腿、小腿，和足，单位为mm；围径包括头围、胸围、腰围和臀围，单位为mm；体积包括15 个环节中每个环节的体积以及整体的体积，共10 项，单位为cm3；质量包括15 个环节中每个环节的质量，共9 项，单位为kg；质心包括15 个环节中每个环节的以及整体的质心，共10 项，单位为mm；转动惯量中不包括手和足环节，但包括整体的转动惯量，因此共8 项，单位为kg·mm2。

4.2 查询系统结构图

查询系统是对给定性别（男、女）、类别（成年）以及输入身高和体重两个基本尺寸的值来得到各环节的主要参数尺寸。查询系统结构图如图2 所示。

4.3 查询系统使用实例

以一实例来说明查询系统使用。对给定我国成年男性身高为1704mm，体重为68kg，查询各环节的长度尺寸、质量和质心尺寸结果如图3、图4 所示。

图2 查询系统结构图

图3 各环节长度尺寸查询结果

5 结束语

基于二元线性回归的人体尺寸查询系统的设计开发，能够在已知身高和体重两基本尺寸参数之后，快速获得所需要的人体各环节主要尺寸参数，为产品人性化设计过程中获取人体尺寸提供方便。该查询系统可广泛的应用在人体模型制作行业、服装行业、驾驶舱空间设计、座椅产品设计、操作杆件设计、家居卫浴产品设计等行业，同时特别适用于个性化定制要求高的行业，系统的推广可以缩短设计周期，有效降低开发成本，具有良好应用前景。

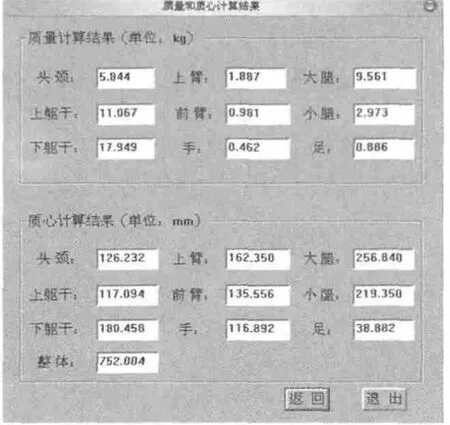
图4 各环节长度尺寸查询结果

[1] 梁艳霞. 人体尺度在产品设计中的应用-以双层床的设计为例[J].郑州轻工业学院学报（社会科学版），2009，4.

[2] 郭凤艳，安学锋.企业统计学[M].北京:经济管理出版社，2001.

[3] 王继先，等.中国参考人解剖生理和代谢数据[M].北京:原子能出版社，1998.

[4] 丁玉兰.人机工程学[M].北京：北京理工大学出版社，2011.

[5] 张春红，林大全.中国成年仿真人体模型的参数研究[J].机械，2009，7.

[6] 刘静民.中国成年人人体惯性参数国家标准的制定[D].北京:北京体育大学，2004.

[7] 陈平雁，等.SPSS 13.0 统计软件应用教程[M].北京:人民卫生出版社，2005.